Consideremos un sistema aislado compuesto por un gran número de partículas, en el cual, cada partícula puede ocupar alguno de los niveles de energía E₀, E₁, E₂, .... Estos pueden estar cuantizados (como los estados rotacionales o vibracionales de una molécula) o bien, pueden formar un espectro continuo (como la energía cinética de las moléculas de un gas).

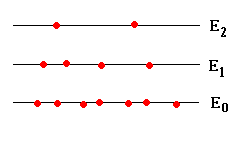
La energía del nivel i será E_i=i·ε, siendo ε la diferencia de energía entre dos niveles consecutivos.

En un momento dado, las partículas están distribuidas entre los diferentes niveles de modo que n₀ tienen energía E₀, n₁ partículas tienen energía E₁ y así, sucesivamente.

El número total de partículas es: N=n₀+n₁+n₂+...
Por ser el sistema aislado, la energía total U permanece constante. U=n₀E₀+n₁E₁+n₂E₂+...

Debido a las interacciones y a las colisiones entre las moléculas, los números n₀, n₁, n₂,... están cambiando continuamente. Se puede suponer, que para cada estado macroscópico del sistema, hay una distribución de partículas entre los diversos niveles que es más probable que cualquier otra. Una vez alcanzada esta distribución se dice que el sistema está en equilibrio.

Los números n₀, n₁, n₂,... pueden entonces fluctuar alrededor de los valores correspondientes a la situación de equilibrio sin que se produzcan efectos macroscópicos.

Vamos a determinar el modo en que las partículas de un sistema aislado se distribuyen entre los niveles de energía permitidos.

Conceptos básicos

Macroestado: un gas encerrado en un recipiente de volumen V contiene N moléculas, su presión es p y su temperatura T. Si es un gas ideal estas tres variables termodinámicas están relacionadas pV=NkT. Si su energía interna es U entonces U=(3/2)kT, donde k es la constante de Boltzmann.

Microestado: a nivel microscópico tendremos que especificar la posición y velocidad de cada molécula individual. Si conocemos el sistema a nivel microscópico determinamos las variables termodinámicas como la energía interna, suma de las energías de todas las moléculas.

El número de microestados Ω(U,V,N) que se corresponden con un macroestado dado, se denomina multiplicidad del macroestado. Este número como veremos es muy grande incluso para sistemas compuestos por un número pequeño de partículas, ya que hay un número muy grande de diferentes formas de distribuir una cantidad dada de energía entre las moléculas del sistema.

El postulado quiere decir que la probabilidad de encontrar al sistema en un micoroestado dado es 1/Ω, ya que todos los Ω son igualmente probables.

El sólido de Einstein

Se elige este sistema ideal ya que es el que nos permite calcular la función Ω(U,V,N) de la forma más simple.

Sea N el número de osciladores unidimensionales, la energía de un oscilador es E=nε, siendo n un número entero no negativo. Cada oscilador puede almacenar un número n de unidades ε de energía.

La energía total del sólido es U=qε, siendo q un número entero no negativo.

El número de microestados Ω correspondientes a un macroestado dado caracterizado por N osciladores y q unidades de energía es

${\displaystyle \Omega (N,q)=\left(\begin{array}{c}q+N-1\\ q\end{array}\right)=\frac{(q+N-1)!}{q!(N-1)!}}$

Por ejemplo, sea un sólido compuesto de N=3 partículas cuya energía total es q=3 unidades. Vamos a comprobar que, tenemos 10 maneras diferentes de repartir tres unidades de energía entre tres osciladores.

function r=combinatorio(n,m)
    k=1:m;
    t=(n-k+1)./k;
    r=prod(t);
end

N=3; %cajas (osciladores)
q=3; %bolas (unidades de energía)
omega=combinatorio(q+N-1,q);
cajas=zeros(omega,N);
i=0;
bIgual=0;
for x=0:q
    for y=0:q
        if x+y>q 
            continue
        end
        bIgual=0;
        for j=1:i
            if x==cajas(i,1) && y==cajas(i,2) 
                bIgual=1;
                break
            end
        end
        if bIgual
            continue
        end
        i=i+1;
        cajas(i,1)=x;
        cajas(i,2)=y;
        cajas(i,3)=q-x-y;
    end
end

cajas =
     0     0     3
     0     1     2
     0     2     1
     0     3     0
     1     0     2
     1     1     1
     1     2     0
     2     0     1
     2     1     0
     3     0     0

• La primera línea [0,0,3], indica, tres unidades de energía en el tercer oscilador y no hay energía en los otros dos osciladores (tres bolas en la tercera caja)
• La segunda línea [0,1,2], indica, una unidad de energía en el segundo oscilador, dos unidades de energía en el tercer oscilador (una bola en la segunda caja, dos en la tercera)
• La línea [1,1,1], indica, que una unidad de energía se reparte entre cada uno de los tres osciladores (una bola en cada caja)
• y así, sucesivamente

Nota: El código del script es válido solamente para N=3 osciladores (cajas) y para cualquier número de unidades de energía q (bolas). Se podría elaborar un código similar para N=4, e incluso, para un N cualesquiera. Para N>3 la multiplicidad se puede hacer muy elevada y no tiene interés producir una larga lista de microestados para un macroestado dado.

Dos sólidos de Einstein

Consideremos dos sólidos A y B que pueden interaccionar entre ellos, intercambiado energía entre sus partículas, pero en conjunto forman un sistema aislado.

Supondremos que este intercambio es muy pequeño (débilmente acoplados) comparado con el intercambio de energía entre los osciladores de cada uno de los sólidos, de modo que la energía de cada uno de los dos subsistemas U_A y U_B cambia muy poco con el tiempo. Vamos a calcular la multiplicidad del sistema combinado cuya energía es U=U_A+U_B y el número total de partículas N=N_A+N_B

Supongamos el sistema formado por dos subsistemas cada uno de tres osciladores, N_A=N_B=3. La energía total del sistema es de 6 unidades, q=q_A+q_B=6

Para cada uno de los siete macroestados q_A=0,1,...6, calculamos la multiplicidad del sistema combinado como producto de las multiplicidades de los sistemas individuales, Ω=Ω_A·Ω_B

NA=3; %cajas (osciladores) del subsistema A
NB=3; %cajas (osciladores) del subsistema B
qt=6; %bolas (unidades de energía total)
omega=zeros(1,qt+1);
i=0;
for q=0:qt
    i=i+1;
    omega(i)=combinatorio(q+NA-1,q)*combinatorio(qt-q+NB-1,qt-q);
end
bar(0:qt,omega);
grid on
ylim([0,105])
xlabel('q_A')
ylabel('\Omega_A·\Omega_B')
title('Dos sólidos de Einstein')

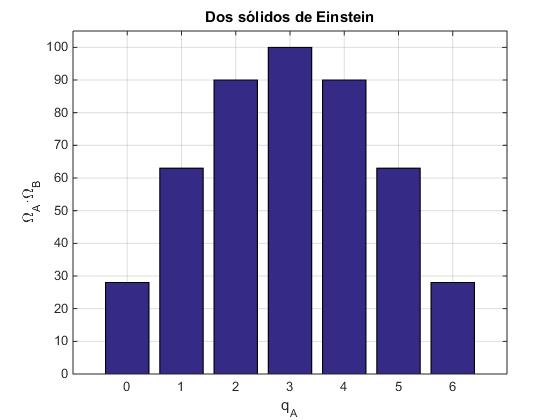
>> omega =
    28    63    90   100    90    63    28
>> sum(omega)
ans =  462

El número de microestados del sistema formado por N=6 partículas con q=6 unidades de energía se obtiene del número combinatorio

${\displaystyle \Omega (N,q)=\left(\begin{array}{c}q+N-1\\ q\end{array}\right)=\left(\begin{array}{c}6+6-1\\ 6\end{array}\right)=\left(\begin{array}{c}11\\ 6\end{array}\right)=462}$

En la tabla y en la gráfica, vemos que el cuarto macroestado en el que cada uno de los sólidos tiene tres unidades de energía le corresponde la multiplicidad más elevada, 100. Los 462 microestados son accesibles al sistema combinado y tienen la misma probabilidad 1/462. La probabilidad de encontrar al sistema combinado en el cuarto macroestado es por tanto, 100/462. Los macoestados en los que uno de los dos subsistemas tiene las seis unidades de energía y el otro subsistema ninguna energía, son poco probables 28/462

Combinamos los scripts anteriores para crear otro que nos muestre la lista completa de microestados correspondientes a un macroestado dado. Dado que la lista de microestados es muy larga solamente se muestra en esta página una pequeña porción.

function [cajas,omega] = microestado(q)
    N=3;
    omega=combinatorio(q+N-1,q);
    cajas=zeros(omega,N);
    i=0;
    bIgual=0;
    for x=0:q
        for y=0:q
            if x+y>q 
                continue
            end
            bIgual=0;
            for j=1:i
                if x==cajas(i,1) && y==cajas(i,2) 
                    bIgual=1;
                    break
                end
            end
            if bIgual
                continue
            end
            i=i+1;
            cajas(i,1)=x;
            cajas(i,2)=y;
            cajas(i,3)=q-x-y;
        end
    end
end

qt=6; %bolas (unidades de energía) en total
res=zeros(1,6);
for q=0:qt
    [cajas_A,omega_A]=microestado(q);
    [cajas_B,omega_B]=microestado(qt-q);
    fprintf('Energía subsistema A: %i, multiplicidad: %i\n',q,omega_A);
    fprintf('Energía subsistema B: %i, multiplicidad: %i\n',qt-q,omega_B);
    fprintf('Energía sistema: %i, multiplicidad: %i\n',qt,omega_A*omega_B);
    for i=1:omega_A
        for j=1:omega_B
            res=[cajas_A(i,1:3), cajas_B(j,1:3)];
            disp(res)
        end
    end
end

Un microestado del sistema viene dado por una fila de seis números que suman 6 unidades de energía, los tres primeros corresponden al subsistema A y los tres últimos, al subsistema B

Energía subsistema A: 0, multiplicidad: 1
Energía subsistema B: 6, multiplicidad: 28
Energía sistema: 6, multiplicidad: 28
     0     0     0     0     0     6
     0     0     0     0     1     5
     ...............................
     0     0     0     5     1     0
     0     0     0     6     0     0

Energía subsistema A: 1, multiplicidad: 3
Energía subsistema B: 5, multiplicidad: 21
Energía sistema: 6, multiplicidad: 63
     0     0     1     0     0     5
     0     0     1     0     1     4
     1     0     0     0     0     5
     ...............................
     1     0     0     4     1     0
     1     0     0     5     0     0

Energía subsistema A: 2, multiplicidad: 6
Energía subsistema B: 4, multiplicidad: 15
Energía sistema: 6, multiplicidad: 90
     0     0     2     0     0     4
     0     0     2     0     1     3
     1     0     1     0     0     4
     1     1     0     4     0     0
     2     0     0     0     0     4
     2     0     0     0     1     3
    ................................
     2     0     0     4     0     0

Energía subsistema A: 3, multiplicidad: 10
Energía subsistema B: 3, multiplicidad: 10
Energía sistema: 6, multiplicidad: 100
     0     0     3     0     0     3
     1     0     2     0     0     3
     1     0     2     0     1     2
     2     0     1     0     0     3
     ...............................
     2     1     0     3     0     0
     3     0     0     0     0     3
     3     0     0     2     1     0
     3     0     0     3     0     0

Energía subsistema A: 4, multiplicidad: 15
Energía subsistema B: 2, multiplicidad: 6
Energía sistema: 6, multiplicidad: 90
     0     0     4     0     0     2
     1     0     3     0     0     2
     1     0     3     0     1     1
     2     0     2     0     0     2
     2     2     0     2     0     0
     3     0     1     0     0     2
     ..............................
     3     1     0     2     0     0
     4     0     0     0     0     2
     4     0     0     2     0     0

Energía subsistema A: 5, multiplicidad: 21
Energía subsistema B: 1, multiplicidad: 3
Energía sistema: 6, multiplicidad: 63
     0     0     5     0     0     1
     1     0     4     0     0     1
     1     0     4     0     1     0
    ................................
     2     2     1     0     1     0
     2     3     0     1     0     0
     3     2     0     0     1     0
     3     2     0     1     0     0
     4     1     0     1     0     0
     5     0     0     0     1     0
     5     0     0     1     0     0

Energía subsistema A: 6, multiplicidad: 28
Energía subsistema B: 0, multiplicidad: 1
Energía sistema: 6, multiplicidad: 28
     0     0     6     0     0     0
     1     0     5     0     0     0
     2     0     4     0     0     0
     2     1     3     0     0     0
     ................................
     3     0     3     0     0     0
     3     3     0     0     0     0
     4     0     2     0     0     0
     5     0     1     0     0     0
     5     1     0     0     0     0
     6     0     0     0     0     0

Consideremos ahora, un sistema más grande formado por dos subsistemas de N_A=300 y N_B=200, con una energía total q=q_A+q_B=100 a repartir entre los osciladores N_A y N_B de ambos subsistemas

qt=100; %unidades de energía (total)
NA=300; %osciladores del subsistema A
omega_A=zeros(1,qt+1);
i=0;
for qA=0:qt
    i=i+1;
    omega_A(i)=combinatorio(qA+NA-1,qA);
end
NB=200; %osciladores del subsistema B
omega_B=zeros(1,qt+1);
i=0;
for qB=qt:-1:0
    i=i+1;
    omega_B(i)=combinatorio(qB+NB-1,qB);
end
plot(0:qt,omega_A.*omega_B)
grid on
xlabel('q_A')
ylabel('\Omega_A·\Omega_B')
title('Dos sólidos de Einstein')

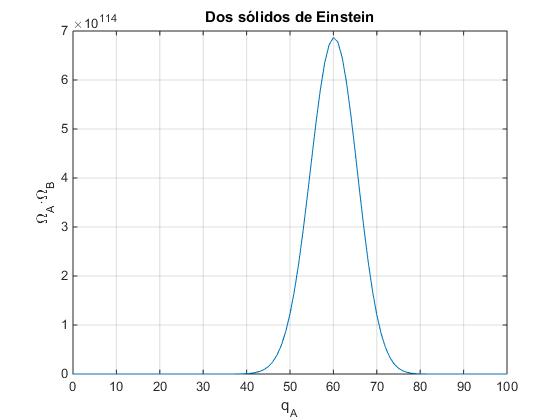
Vemos que las multiplicidades son números muy grandes, la multiplicidad presenta un máximo para el macroestado en el que el subsistema A tiene q_A=60 y el subsistema B, q_B=40. Si el sistema está inicialmente en un macroestado con probabilidad muy pequeña, (por ejemplo, el subsistema A con cero energía y el B con 100 unidades de energía) los dejamos interaccionar, al cabo de un tiempo se encontrarán cerca del macroestado más probable (máxima multiplicidad). La energía fluirá desde las partículas del subsistema B hacia las partículas de subsistema A. El proceso se denomina irreversible

Entropía

En vez de trabajar con multiplicidades que son números muy grandes, es conveniente definir la entropía del sistema como

S=k·log(Ω)

donde k es la constante de Boltzmann. La entropía es una magnitud aditiva

S=k·log(Ω_A·Ω_B)=k·log(Ω_A)+k·log(Ω_B)=S_A+S_B

qt=100; %unidades de energía (total)
NA=300; %osciladores del subsistema A
omega_A=zeros(1,qt+1);
i=0;
for qA=0:qt
    i=i+1;
    omega_A(i)=combinatorio(qA+NA-1,qA);
end
NB=200; %osciladores del subsistema B
omega_B=zeros(1,qt+1);
i=0;
for qB=qt:-1:0
    i=i+1;
    omega_B(i)=combinatorio(qB+NB-1,qB);
end
hold on
plot(0:qt,log(omega_A))
plot(0:qt,log(omega_B))
plot(0:qt,log(omega_A)+log(omega_B))
hold off
legend('S_A','S_B','S_t', 'location','northwest')
xlabel('q_A')
ylabel('S')
title('Dos sólidos de Einstein')

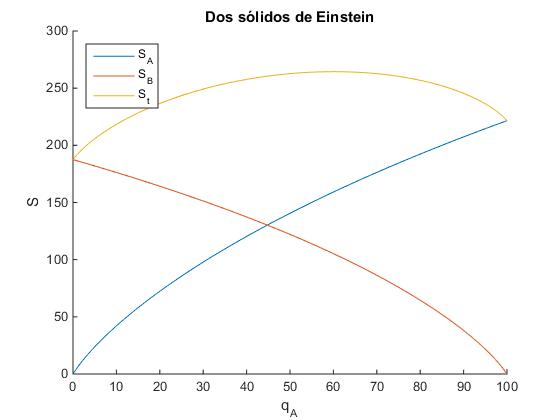
Temperatura

Se dice que dos subsistemas que pueden interaccionar que están en equilibrio térmico si están a la misma temperatura. Si un subsistema tiene una temperatura más alta que el otro, la energía fluye del primero hacia el segundo hasta que se alcanza el equilibrio térmico. En el estado de equilibrio, los intercambios de energía entre las partículas de ambos subsistemas se siguen produciendo, pero no dan lugar a un cambio de su temperatura.

El equilibrio térmico se produce cuando la entropía total S (o la multiplicidad Ω) alcanza su valor máximo, cuando la derivada dS/dq_A=0

${\displaystyle \begin{array}{l}S=S_A+S_B\frac{dS}{d{q}_A}=\frac{d{S}_A}{d{q}_A}+\frac{d{S}_B}{d{q}_A}\\ 0=\frac{d{S}_A}{d{q}_A}+\frac{d{S}_B}{d{q}_A}\\ \frac{d{S}_A}{d{q}_A}=-\frac{d{S}_B}{d{q}_A}\end{array}}$

Consideremos el sistema formado por N=50 osciladores con unidades de energía q que van desde 0 a 100. Calculamos la multiplicidad para valor de q, representamos su logaritmo (la entropía) en función de q

N=50;
S=zeros(1,101);
i=0;
for q=0:100
    i=i+1;
    S(i)=log(combinatorio(q+N-1,q));
end
plot(0:100,S)
grid on
xlabel('q')
ylabel('S')
title('Entropía')

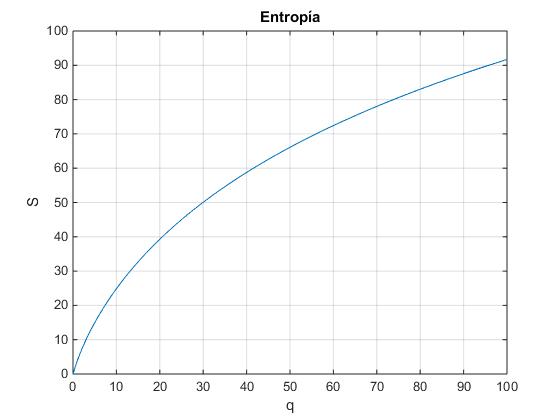
Para calcular la temperatura T=Δq/ΔS, a partir de una tabla de valores (q,S) nos fijamos en el siguiente esquema, para calcular la inversa de la pendiente de un segmento de recta de color rojo

${\displaystyle T_i=\frac{q_{i+1}-q_{i-1}}{S_{i+1}-S_{i-1}}=\frac{2}{S_{i+1}-S_{i-1}}}$

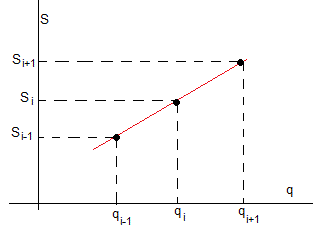
De un modo similar, se calcula la capacidad calorífica, C=ΔU/ΔT

${\displaystyle C_i=\frac{q_{i+1}-q_{i-1}}{T_{i+1}-T_{i-1}}=\frac{2}{T_{i+1}-T_{i-1}}}$

N=50;
S=zeros(1,101);
i=0;
for q=0:100
    i=i+1;
    S(i)=log(combinatorio(q+N-1,q));
end

T=zeros(1,100);
for i=2:100
    T(i)=2/(S(i+1)-S(i-1));
end
C=zeros(1,99);
for i=3:99
    C(i)=2/(T(i+1)-T(i-1))/N;
end
plot(T(3:99),C(3:99))
grid on
xlabel('T')
ylabel('C')
title('Capacidad calorífica')

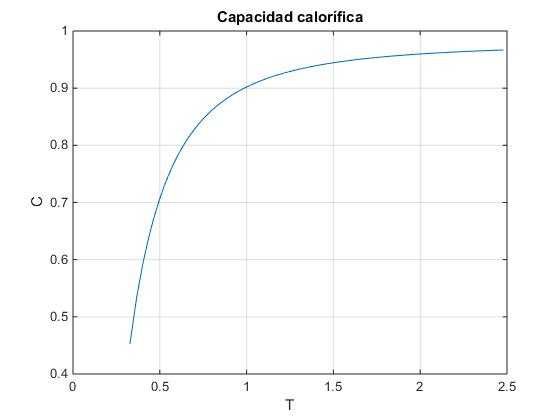
La capacidad calorífica a altas temperaturas es constante tal como prevée el teorema de equipartición.

La fórmula de la distribución de Boltzmann

Supongamos un sistema formado por dos subsistemas: un oscilador N_A=1 en contacto con otro mucho más grande N_B=1000. La energía total es q_A+q_B=100.

La multiplicidad Ω=Ω_A·Ω_B, como Ω_A=1 (un oscilador), Ω=Ω_B

Representamos log(Ω)=log(Ω_B)=S_B en función de q_A=100-q_B

NB=1000;
S_B=zeros(1,101);
i=0;
for qB=100:-1:0
    i=i+1;
    S_B(i)=log(combinatorio(qB+NB-1,qB));
end
plot(0:20,S_B(1:21),'ro','markersize',4,'markerfacecolor','r')
grid on
xlabel('q_A')
ylabel('log(\Omega)')
title('Factor de Boltzmann')

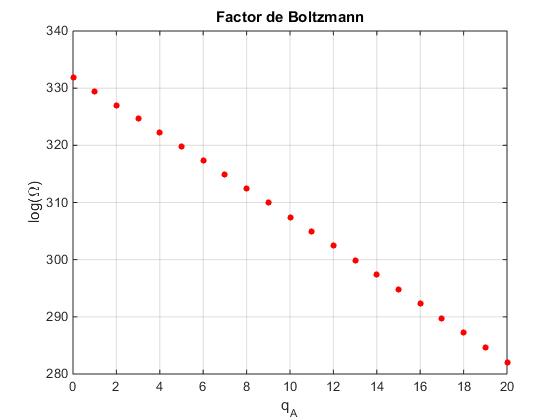
Los puntos se sitúan sobre una recta de pendiente negativa, que vamos a determinar

Como U_A=q_A·ε, S_B=k·log(Ω) y U_A+U_B=constante (100 unidades de energía)

${\displaystyle \frac{\partial \ln (\Omega )}{\partial q_A}=\frac{\epsilon }{k}\frac{\partial S_B}{\partial U_A}=-\frac{\epsilon }{k}\frac{\partial S_B}{\partial U_B}=-\frac{\epsilon }{k{T}_B}}$

La multiplicidad total Ω, proporcional a la probabilidad de encontrar el subsistema A en un macroestado dado, decrece exponencialmente con la energía E=q_A·ε

Sólido paramagnético. Dos estados de energía

Terminamos esta página examinado el comportamiento de un sólido paramagnético con dos posibles niveles de energía

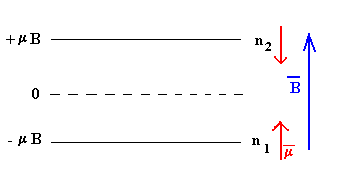
La energía de un átomo de momento magnético μ en el campo magnético B viene dado por el producto escalar

E=-μ·B

• Para los n₁ átomos cuyo momento μ es paralelo a B la energía de cada uno vale E₁=-μB
• Para los n₂ átomos cuyo momento μ es antiparalelo a B la energía de cada uno vale E₂=+μB

La energía total del sistema U=n₁·E₁+n₂·E₂=(N-2n₁)·μB

La magnetización es M=n₁·μ+n₂·(-μ)=-(N-2n₁)·μ=-U/B

Multiplicidad

La multiplicidad de un macroestado con n₁ partículas en el nivel inferior y N-n₁ en el nivel superior es

${\displaystyle \Omega (N,n_1)=\left(\begin{array}{c}N\\ n_1\end{array}\right)=\frac{N!}{n_1!(N-n_1)!}}$

Examinamos un sistema de N=100 partículas. La energía U varía entre -100 unidades cuando n₁=100 (todas las partículas ocupan el nivel inferior de energía) y 100 unidades, cuando n₁=0 (todas las partículas están en el nivel superior de energía). Representamos la entropía S en función de la energía U

N=100;
S=zeros(1,N+1);
i=0;
for n1=N:-1:0
    i=i+1;
    S(i)=log(combinatorio(N,n1));
end
plot(-N:2:N,S)
grid on
xlabel('Energía')
ylabel('Entropía')
title('Dos estados')

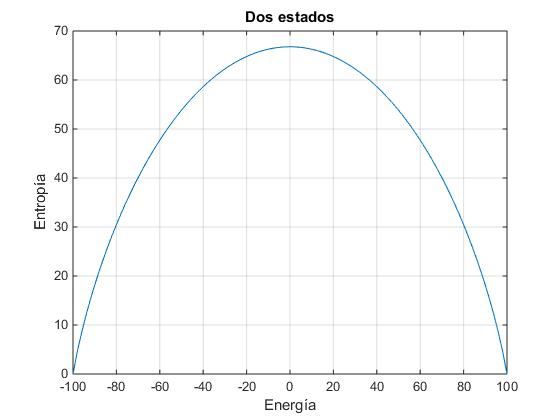
La temperatura es inversamente proporcional a la pendiente de la curva. La pendiente va decreciendo a medida que se incrementa la energía hasta que se hace cero cuando U=0, la temperatura se hace infinita

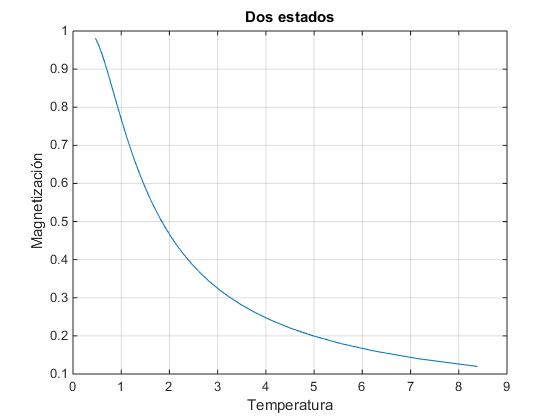
Representamos la magnetización M en función de la temperatura. Vemos que M tiende hacia cero cuando la temperatura se incrementa

N=100;
S=zeros(1,N+1);
i=0;
for n1=N:-1:0
    i=i+1;
    S(i)=log(combinatorio(N,n1));
end
T=zeros(1,N);
for i=2:N
    T(i)=4/(S(i+1)-S(i-1));
end

M=(N:-2:-N)/N;
plot(T(T>0 & T<10),M(T>0 & T<10))
grid on
xlabel('Temperatura')
ylabel('Magnetización')
title('Dos estados')

Representamos el calor específico C en función de la temperatura

N=100;
S=zeros(1,N+1);
i=0;
for n1=N:-1:0
    i=i+1;
    S(i)=log(combinatorio(N,n1));
end
T=zeros(1,N);
for i=2:N
    T(i)=4/(S(i+1)-S(i-1));
end
C=zeros(1,N-1);
for i=3:N-1
    C(i)=4/(T(i+1)-T(i-1))/N;
end
plot(T(T>0 & T<10),C(T>0 & T<10))
grid on
xlabel('Temperatura')
ylabel('Calor específico')
title('Dos estados')

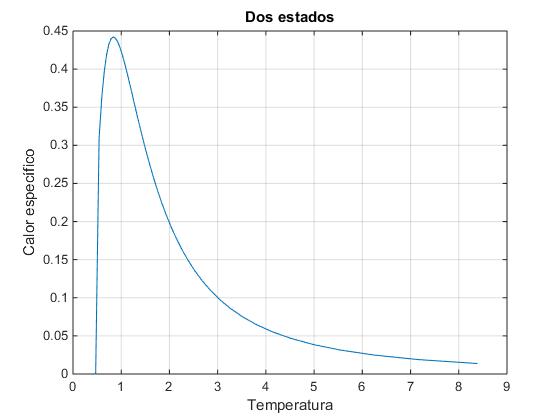
Probabilidad

Los átomos pueden estar en uno u otro de los dos niveles de energía E₁ y E₂. Aplicando la fórmula de la de Boltzmann calculamos la proporción de átomos n₁/N y n₂/N que ocupan cada uno de los dos niveles de energía

${\displaystyle \frac{n_1}{N}\propto \text{exp}\left(-\frac{E_1}{kT}\right)\frac{n_2}{N}\propto \text{exp}\left(-\frac{E_2}{kT}\right)}$

La constante de proporcionalidad se determina sabiendo que n₂/N+n₁/N=1

${\displaystyle \frac{n_1}{N}=\frac{\text{exp}\left(-\frac{E_1}{kT}\right)}{\text{exp}\left(-\frac{E_1}{kT}\right)+\text{exp}\left(-\frac{E_2}{kT}\right)}=\frac{1}{1+\text{exp}\left(-\frac{2\mu B}{kT}\right)}}$

n₁ es mayor que n₂, ya que la exponencial decreciente en el denominador no puede ser mayor que la unidad, ni menor que cero. Por tanto, hay más átomos con el momento paralelo al campo magnético que con el momento magnético apuntando en sentido contrario al campo. La sustancia presenta un momento magnético no nulo.

${\displaystyle \begin{array}{l}M=\frac{n_1}{N}\mu +\frac{n_2}{N}(-\mu )\\ M=\mu \frac{1-\text{exp}\left(-\frac{2\mu B}{kT}\right)}{1+\text{exp}\left(-\frac{2\mu B}{kT}\right)}\end{array}}$

Como $\frac{\mu B}{kT}$ es mucho menor que la unidad (por ejemplo, si B=1 T y la temperatura T=300 K el cociente vale 0.0045. Téngase en cuenta que μ_B=9.3 10^-24 A m², y k=1.38 10^-23 J/K), utilizando el desarrollo en serie e^x=1+x+... se obtiene

${\displaystyle M=\frac{{\mu }^{2}B}{kT}}$

El momento magnético medio es inversamente proporcional a la temperatura absoluta de la sustancia, el comportamiento de los materiales paramagnéticos.

Calaculamos el calor específico de este sólido

${\displaystyle \begin{array}{l}U=n_1{E}_1+n_2{E}_2\\ U=-N\mu B\frac{1-\exp \left(-\frac{2\mu B}{kT}\right)}{1+\exp \left(-\frac{2\mu B}{kT}\right)}\\ C=\frac{1}{N}\frac{\partial U}{\partial T}=2\mu B\frac{2\mu B}{k{T}^2}\frac{\exp \left(-\frac{2\mu B}{kT}\right)}{{\left(1+\exp \left(-\frac{2\mu B}{kT}\right)\right)}^2}\end{array}}$

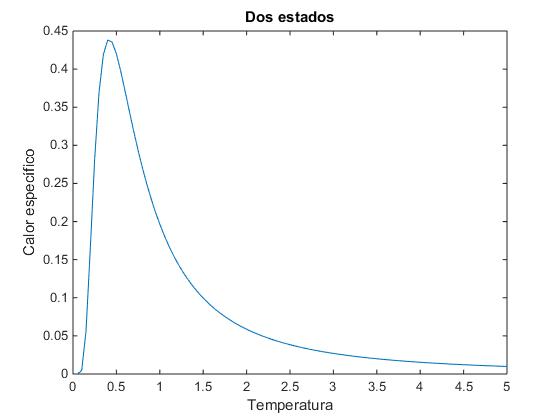
El calor específico es una función de la temperatura (x)

${\displaystyle C\propto \frac{\exp \left(-1/x\right)}{x^2{\left(1+\exp \left(-1/x\right)\right)}^2}}$

Representamos esta función y vemos que tiene la misma apariencia que la calculada mediante la multiplicidad

>> f=@(x) (exp(-1./x)./x.^2)./(1+exp(-1./x)).^2;
>> x=0:0.05:5;
>> plot(x,f(x))
>> xlabel('Temperatura')
>> ylabel('Calor específico')
>> title('Dos estados')

Referencias

Thomas A. Moore, Daniel V. Schroeder. A different approach to introducing statistical mechanics. Am. J. Phys. 65 (1), January 1997