Concepto de temperatura

La temperatura es la sensación física que nos produce un cuerpo cuando entramos en contacto con él.

Observamos cambios en los cuerpos cuando cambian su temperatura, por ejemplo, la dilatación que experimenta un cuerpo cuando incrementa su temperatura. Esta propiedad se usa para medir la temperatura de un sistema. Pensemos en los termómetros que consisten en un pequeño depósito de mercurio que asciende por un capilar a medida que se incrementa la temperatura.

Concepto de calor

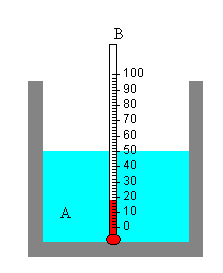
Cuando dos cuerpos A y B que tienen diferentes temperaturas se ponen en contacto térmico, después de un cierto tiempo, alcanzan la condición de equilibrio en la que ambos cuerpos están a la misma temperatura.

Supongamos que la temperatura del cuerpo A es mayor que la del cuerpo B, T_A>T_B.

Observaremos que la temperatura de B se eleva hasta que se hace casi igual a la de A. En el proceso inverso, si el objeto B tiene una temperatura T_B>T_A, el baño A eleva un poco su temperatura hasta que ambas se igualan.

Cuando un sistema de masa grande se pone en contacto con un sistema de masa pequeña que está a diferente temperatura, la temperatura de equilibrio resultante está próxima a la del sistema grande.

Decimos que una cantidad de calor ΔQ se transfiere desde el sistema de mayor temperatura al sistema de menor temperatura.

• La cantidad de calor transferida es proporcional al cambio de temperatura ΔT.
• La constante de proporcionalidad C se denomina capacidad calorífica del sistema.

ΔQ=C·ΔT

Si los cuerpos A y B son los dos componentes de un sistema aislado, el cuerpo que está a mayor temperatura transfiere calor al cuerpo que está a menos temperatura hasta que ambas se igualan

Si T_A>T_B

• El cuerpo A cede calor: ΔQ_A=C_A·(T-T_A), entonces ΔQ_A<0
• El cuerpo B recibe calor: ΔQ_B=C_B·(T-T_B), entonces ΔQ_B>0

Como ΔQ_A+ΔQ_B=0

La temperatura de equilibrio, se obtiene mediante la media ponderada

${\displaystyle T=\frac{C_A{T}_A+C_B{T}_B}{C_A+C_B}}$

La capacidad calorífica de la unidad de masa se denomina calor específico c. C=mc

La fórmula para la transferencia de calor entre los cuerpos se expresa en términos de la masa m, del calor específico c y del cambio de temperatura.

ΔQ=m·c·(T_f-T_i)

donde T_f es la temperatura final y T_i es la temperatura inicial.

El calor específico es la cantidad de calor que hay que suministrar a un gramo de una sustancia para que eleve en un grado centígrado su temperatura.

Joule demostró la equivalencia entre calor y trabajo 1cal=4.186 J. Por razones históricas la unidad de calor no es la misma que la de trabajo, el calor se suele expresar en calorías.

El calor específico del agua es c=1 cal/(g ºC). Hay que suministrar una caloría para que un gramo de agua eleve su temperatura en un grado centígrado.

Calor específico de un sólido

Cuando varios cuerpos a diferentes temperaturas se encuentran en un recinto adiabático se producen intercambios caloríficos entre ellos alcanzándose la temperatura de equilibrio al cabo de cierto tiempo. Cuando se ha alcanzado este equilibrio se debe cumplir que la suma de las cantidades de calor intercambiadas es cero.

Se define calor específico c como la cantidad de calor que hay que proporcionar a un gramo de sustancia para que eleve su temperatura en un grado centígrado. En el caso particular del agua c vale 1 cal/(g ºC) ó 4186 J(kg ºK).

La unidad de calor específico que más se usa es cal/(g ºC) sin embargo, debemos de ir acostumbrándonos a usar el Sistema Internacional de Unidades de Medida, y expresar el calor específico en J/(kg·K). El factor de conversión es 4186.

Fuente: Koshkin N. I., Shirkévich M. G.. Manual de Física Elemental. Editorial Mir 1975, pág 74-75

La cantidad de calor recibido o cedido por un cuerpo se calcula mediante la siguiente fórmula

Q=m·c·(T_f-T_i)

Donde m es la masa, c es el calor específico, T_i es la temperatura inicial y T_f la temperatura final

• Si T_i>T_f el cuerpo cede calor Q<0
• Si T_i<T_f el cuerpo recibe calor Q>0

La experiencia se realiza en un calorímetro consistente en un vaso (Dewar) o en su defecto, convenientemente aislado. El vaso se cierra con una tapa hecha de material aislante, con dos orificios por los que salen un termómetro y el agitador.

Supongamos que el calorímetro está a la temperatura inicial T₀, y sea

• m_v es la masa del vaso del calorímetro y c_v su calor específico.
• m_t la masa de la parte sumergida del termómetro y c_t su calor específico
• m_a la masa de la parte sumergida del agitador y c_a su calor específico
• M la masa de agua que contiene el vaso, su calor específico es la unidad

Por otra parte:

Sean m y c las masa y el calor específico del cuerpo problema a la temperatura inicial T.

En el equilibrio a la temperatura T_e se tendrá la siguiente relación.

(M+m_v·c_v+m_t·c_t+m_a·c_a)(T_e-T₀)+m·c(T_e-T)=0

La capacidad calorífica del calorímetro es

k=m_v·c_v+m_t·c_t+m_a·c_a

se le denomina equivalente en agua del calorímetro y se expresa en gramos de agua.

Por tanto, representa la cantidad de agua que tiene la misma capacidad calorífica que el vaso del calorímetro, parte sumergida del agitador y del termómetro y es una constante para cada calorímetro.

El calor específico desconocido del será por tanto

${\displaystyle c=\frac{(M+k)(T_e-T_0)}{m(T-T_e)}}$

En esta fórmula tenemos una cantidad desconocida k, que debemos determinar experimentalmente.

Determinación del equivalente en agua del calorímetro

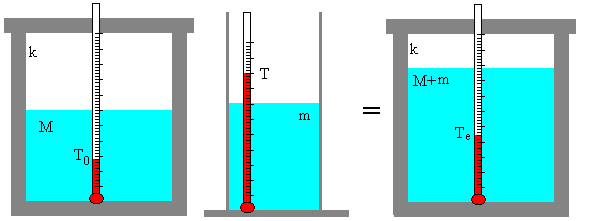
Se ponen M gramos de agua en el calorímetro, se agita, y después de un poco de tiempo, se mide su temperatura T₀. A continuación, se vierten m gramos de agua a la temperatura T. Se agita la mezcla y después de un poco de tiempo, se mide la temperatura de equilibrio T_e.

Como el calorímetro es un sistema adibáticamente aislado tendremos que

(M+k)(T_e-T₀)+m(T_e-T)=0

${\displaystyle k=\frac{m(T-T_e)}{T_e-T_0}-M}$

Determinación del calor específico del sólido

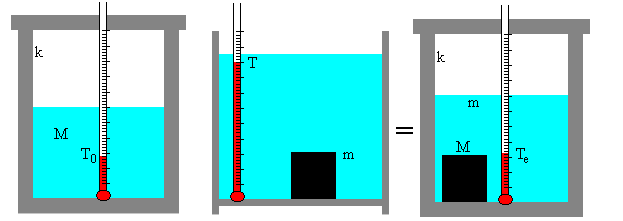
1. Se pesa con una balanza una pieza de material sólido de calor específico c desconocido, resultando m su masa. Se pone la pieza en agua casi hirviendo a la temperatura T.
2. Se ponen M gramos de agua en el calorímetro, se agita y después de poco de tiempo, se mide su temperatura T₀.
3. Se deposita rápidamente la pieza de sólido en el calorímetro. Se agita, y después de un cierto tiempo se alcanza la temperatura de equilibrio T_e.

Se apuntan los datos y se despeja c de la fórmula que hemos deducido en el primer apartado.

${\displaystyle c=\frac{(M+k)(T_e-T_0)}{m(T-T_e)}}$

La experiencia real se debe hacer con mucho cuidado, para que la medida del calor específico sea suficientemente precisa. Se ha de tener en cuenta el intercambio de calor entre el calorímetro y la atmósfera que viene expresadas por la denominada ley del enfriamiento de Newton.

Actividades

1. Medida del equivalente en agua del calorímetro

El programa interactivo genera un número al azar que representa el equivalente en agua del calorímetro.

Introducimos los siguientes datos:

• Masa M de agua en gramos en el calorímetro,
• Temperatura T₀ inicial del calorímetro
• Masa m de agua en gramos en una probeta
• Temperatura T del agua

Se pulsa el botón titulado Prepara, los termómetros y las escalas graduadas de medida del volumen de agua reflejan los valores introducidos.

Si estamos conformes con los datos introducidos, se pulsa el botón titulado Calcula. La masa m de agua se vierte en el calorímetro y el termómetro mide la temperatura final de equilibrio T_e.

Ejemplo:

• Sea M=150 g, T₀=18ºC
• Sea m=70 g, y T=80ºC
• La temperatura de equilibrio es T_e=34ºC

El equivalente en agua del calorímetro será

${\displaystyle k=\frac{70(80-34)}{34-18}-150=51\text{g}}$

2. Medida del calor específico del sólido

Introducimos los siguientes datos:

• Masa M de agua en gramos en el calorímetro,
• Temperatura T₀ inicial del calorímetro
• Masa m del sólido en gramos
• Temperatura T del sólido en el baño
• Elegimos en material del sólido en el control titulado Sólido: Aluminio, Cobre, Estaño, Hierro, Oro, Plata, Plomo.

Se pulsa el botón titulado Prepara.

Si estamos conformes con los datos introducidos, se pulsa el botón titulado Calcula. El sólido se introduce en el calorímetro y el termómetro mide la temperatura final de equilibrio T_e.

Ejemplo:

• Agua: M=150 g, T₀=18ºC
• Sólido: aluminio, m=70 g, y T=80ºC
• La temperatura final de equilibrio es T_e=22ºC

${\displaystyle c=\frac{(150+51)·(22-18)}{70(80-22)}=0.198\text{cal/(g·ºC)}=0.198·4186=830\text{J/(kg·K)}}$