La ley de enfriamiento de Newton en un recinto de tamaño finito

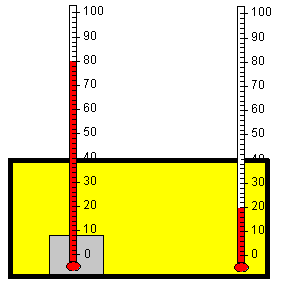
El cuerpo caliente tiene una masa m₁ y su calor específico es c₁, por tanto, su capacidad calorífica es C₁=m₁·c₁. En el instante t su temperatura es T₁
El recinto tiene una masa m₂ y su calor específico es c₂, por tanto, su capacidad calorífica es C₂=m₂·c₂. En el instante t su temperatura es T₂<T₁.

El cuerpo caliente en el intervalo de tiempo entre t y t+dt pierde una cantidad de calor dQ, su temperatura disminuye

dQ=-C₁·dT₁

Como el recinto está térmicamente aislado, en el mismo intervalo de tiempo gana una cantidad de calor dQ y su temperatura aumenta

dQ=C₂·dT₂

El calor perdido por el cuerpo es igual al ganado por el recinto, la temperatura del cuerpo disminuye, la temperatura del recinto aumenta

-C₁·dT₁=C₂·dT₂

Supondremos que la pérdida de calor del cuerpo caliente obedece a la ley del enfriamiento de Newton

$\frac{d Q}{d t} = α S (T_{1} - T_{2})$

Donde α es el coeficiente de intercambio de calor y S es el área del cuerpo.

La ecuación que nos da la variación de la temperatura T₁ del cuerpo con el tiempo es

$- C_{1} \frac{d T_{1}}{d t} = α S (T_{1} - T_{2})$

Para eliminar la variable T₂, derivamos con respecto del tiempo

$\begin{array}{l} C_{1} \frac{d^{2} T_{1}}{d t^{2}} + α S \frac{d T_{1}}{d t} - α S \frac{d T_{2}}{d t} = 0 \\ \frac{d^{2} T_{1}}{d t^{2}} + α S \frac{C_{1} + C_{2}}{C_{1} \cdot C_{2}} \frac{d T_{1}}{d t} = 0 \\ \frac{d^{2} T_{1}}{d t^{2}} + k \frac{d T_{1}}{d t} = 0 k = α S \frac{C_{1} + C_{2}}{C_{1} \cdot C_{2}} \end{array}$

La solución de la ecuación diferencial es

$\begin{array}{l} T_{1} = A_{1} + B_{1} \cdot \exp (- k \cdot t) \\ \frac{d T_{1}}{d t} = - k B_{1} \exp (- k \cdot t) \end{array}$

Las constantes A₁ y B₁ se determinan a partir de las condiciones iniciales, la temperatura inicial y su derivada. En el instante t=0, la temperatura del cuerpo es T₀₁

A₁+B₁=T₀₁

Su derivada en el instante t=0 vale

$\begin{array}{l} {- C_{1} \frac{d T_{1}}{d t} |}_{t = 0} = α S (T_{01} - T_{02}) \\ C_{1} k B_{1} = α S (T_{01} - T_{02}) \end{array}$

La solución de la ecuación diferencial es

$T_{1} = \frac{C_{1} T_{01} + C_{2} T_{02}}{C_{1} + C_{2}} + \frac{C_{2} (T_{01} - T_{02})}{C_{1} + C_{2}} \exp (- k \cdot t)$

La temperatura T₂ del recinto en función del tiempo se calcula del siguiente modo

$\begin{array}{l} T_{2} = A_{2} + B_{2} \cdot \exp (- k \cdot t) \\ \frac{d T_{2}}{d t} = - k B_{2} \exp (- k \cdot t) \end{array}$

Las constantes A₂ y B₂ se determinan a partir de las condiciones iniciales, la temperatura inicial y su derivada. En el instante t=0, la temperatura del cuerpo es T₀₂

A₂+B₂=T₀₂

Su derivada en el instante t=0 vale

$\begin{array}{l} {- C_{1} \frac{d T_{1}}{d t} |}_{t = 0} = {C_{2} \frac{d T_{2}}{d t} |}_{t = 0} \\ C_{1} k B_{1} = - C_{2} k B_{2} \end{array}$

La temperatura del recinto en función del tiempo es

$T_{2} = \frac{C_{1} T_{01} + C_{2} T_{02}}{C_{1} + C_{2}} - \frac{C_{1} (T_{01} - T_{02})}{C_{1} + C_{2}} \exp (- k \cdot t)$

En la figura, se muestra la evolución de temperaturas del cuerpo T₁ y del recinto T₂ en función del tiempo t.

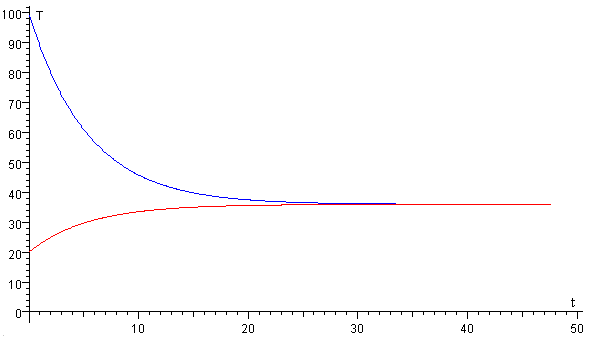
Cuando t→∞, el cuerpo y el recinto alcanzan la misma temperatura que es la media ponderada.

$T_{1} = T_{2} = \frac{C_{1} T_{01} + C_{2} T_{02}}{C_{1} + C_{2}}$

En la práctica, se alcanza el equilibrio al cabo de cierto tiempo que depende del valor de la constante de tiempo τ=1/k. Si la constante de tiempo τ es pequeña, el estado de equilibrio se alcanza después de poco tiempo.

Las temperaturas T₁ del cuerpo y T₂ del recinto se expresan en función del tiempo t.

$\begin{array}{l} T_{1} = \frac{(C_{1} / C_{2}) T_{01} + T_{02}}{(C_{1} / C_{2}) + 1} + \frac{(T_{01} - T_{02})}{(C_{1} / C_{2}) + 1} \exp (- k \cdot t) k = α S \frac{(C_{1} / C_{2}) + 1}{C_{1}} \\ T_{2} = \frac{(C_{1} / C_{2}) T_{01} + T_{02}}{(C_{1} / C_{2}) + 1} - \frac{(C_{1} / C_{2}) (T_{01} - T_{02})}{(C_{1} / C_{2}) + 1} \exp (- k \cdot t) \end{array}$

Cuando la capacidad calorífica del recinto C₂es muy grande (C₁/C₂) →0

$\begin{array}{l} T_{1} = T_{02} + (T_{01} - T_{02}) \exp (- k \cdot t) k = α S \frac{1}{C_{1}} \\ T_{2} = T_{02} \end{array}$

Que es la expresión de la ley del enfriamiento de Newton

Ejemplo:

Temperaturas iniciales: T₀₁=80, T₀₂=20
Capacidades caloríficas (valores relativos): C₁=0.2 y C₂=1-0.2=0.8
La constante de proporcionalidad en la ley del enfriamiento de Newton: αS= 0.0005.

La temperatura de equilibrio y la constante k valen

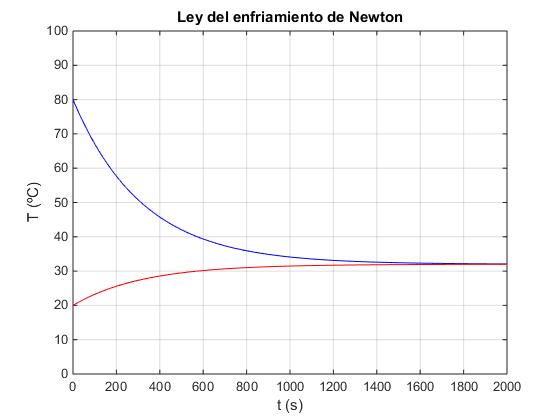
$\begin{array}{l} T_{1} = T_{2} = \frac{0.2 \cdot 80 + 0.8 \cdot 20}{0.2 + 0.8} = 32 ºC \\ k = 0.0005 \cdot \frac{0.2 + 0.8}{0.2 \cdot 0.8} = 0.003125 s^{-1} \end{array}$

Las temperaturas T₁ y T₂ en función del tiempo t

$\begin{array}{l} T_{1} = 32 + 48 \cdot \exp (- t / 320) \\ T_{2} = 32 - 12 \cdot \exp (- t / 320) \end{array}$

T0_1=80; %temperatura inicial del cuerpo
T0_2=20; %temperatura inicial del recinto
C1=0.2; %capacidad calorífica del cuerpo (valores relativos)
C2=1-C1; %capacidad calorífica del recinto
aS=0.0005; %coef. pérdidas
k=aS*(C1+C2)/(C1*C2); %constante

t=0:10:2000;
T1=(C1*T0_1+C2*T0_2)/(C1+C2)+C2*(T0_1-T0_2)*exp(-k*t)/(C1+C2);
T2=(C1*T0_1+C2*T0_2)/(C1+C2)-C1*(T0_1-T0_2)*exp(-k*t)/(C1+C2);
plot(t,T1,'b',t,T2,'r')
ylim([0 100])
grid on
xlabel('t (s)')
ylabel('T (°C)')
title('Ley del enfriamiento de Newton')

Actividades

Se introduce

La temperatura inicial T₀₁ del cuerpo de color azul claro situado a la izquierda, en el control titulado Temperatura A.
La temperatura inicial T₀₂ del cuerpo de color rosa situado a la derecha, en el control titulado Temperatura B.
La posición de la pared divisoria (segmento de color negro) en el control titulado Posición división. Establecemos los valores de sus capacidades caloríficas, C₁ para el cuerpo de color azul claro de la izquierda y C₂=1-C₁ para el cuerpo de color rosa de la derecha.
Se ha fijado el valor de la constante de proporcionalidad en la ley del enfriamiento de Newton, en el valor arbitrario αS= 0.0005.

Posición división:
Temperatura A:
Temperatura B:

Referencias

Maurone P. A., Shiomos C. Newton's law of cooling with finite reservoirs. Am. J. Phys. 51 (9) September 1983, pp. 857-859