Ley del enfriamiento de Newton
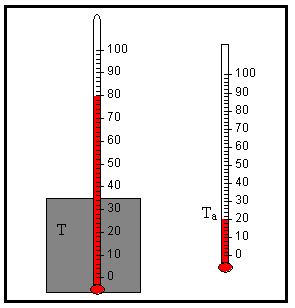
Cuando la diferencia de temperaturas entre un cuerpo y su medio ambiente no es demasiado grande, el calor transferido en la unidad de tiempo hacia el cuerpo o desde el cuerpo por conducción, convección y radiación es aproximadamente proporcional a la diferencia de temperatura entre el cuerpo y el medio externo.
Donde α es el coeficiente de intercambio de calor y S es el área del cuerpo.
Si la temperatura T del cuerpo es mayor que la temperatura del medio ambiente Ta, el cuerpo pierde una cantidad de calor dQ en el intervalo de tiempo comprendido entre t y t+dt, disminuyendo su temperatura T en dT.
dQ=-m·c·dT
donde m=ρ V es la masa del cuerpo (ρ es la densidad y V es el volumen), y c el calor específico.
La ecuación que nos da la variación de la temperatura T del cuerpo en función del tiempo es
o bien,
Integrando esta ecuación con la condición inicial de que en el instante t=0, la temperatura del cuerpo es T0.
Obtenemos la relación lineal siguiente.
ln(T-Ta)=-k·t +ln(T0-Ta)
Despejamos T
T0=90; %temperatura inicial
Ta=10; %temperatura ambiente
k=0.00277; %constante
fplot(@(t) t, @(t) Ta+(T0-Ta)*exp(-k*t),[0,2000],'b')
ylim([0 100])
grid on
xlabel('t (s)')
ylabel('T °C)')
title('Ley del enfriamiento de Newton')
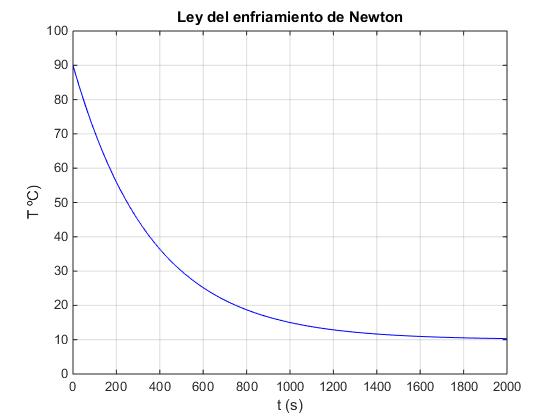
Medida del calor específico de una sustancia
En la deducción anterior, hemos supuesto que el calor específico c no cambia con la temperatura, manteniéndose aproximadamente constante en el intervalo de temperaturas en la que se realiza el experimento.
Si medimos la temperatura del cuerpo durante su enfriamiento a intervalos regulares de tiempo, y realizamos una representación gráfica de ln(T-Ta) en función de t, veremos que los puntos se ajustan a una línea recta, de pendiente –k.
Medimos el área S de la muestra, su masa m=ρV mediante una balanza, y a partir de k calculamos el calor específico c.
Pero tenemos una cantidad desconocida, el coeficiente α , que depende de la forma y el tamaño de la muestra y el contacto entre la muestra y el medio que la rodea. Sin embargo, para varias sustancias metálicas en el aire, α tiene el mismo valor si las formas y los tamaños de todas las muestras son idénticas. Así, se puede determinar α para una sustancia metálica de calor específico conocido y luego, emplear este valor para determinar el calor específico de otra sustancia metálica de la misma forma y tamaño.
En la experiencia simulada, la forma de las muestras ensayadas es cúbica de lado d. El área de las caras de un cubo es S=6d2 y su volumen V=d3. La expresión de la constante k será ahora
La muestra que nos va a servir de referencia es el Aluminio cuya densidad es ρAl=2700 kg/m3 y calor específico cAl=880 J/(K·kg).
Determinamos en una experiencia el valor de kAl para una muestra de Aluminio de forma cúbica de lado d.
Determinamos en otra experiencia la el valor de kx de una muestra de otro material, de densidad ρx conocida, de calor específico cx desconocido, que tenga la misma forma cúbica y del mismo tamaño d.
Como el valor de α es el mismo. El valor del calor específico desconocido cx lo obtenemos a partir de la siguiente relación.
Ejemplo: Determinar el calor específico del Hierro conocido el calor específico del Aluminio.
- Sustancia de referencia Aluminio
- Temperatura inicial T0=100ºC
- Tamaño de la muestra d=10 cm
- Densidad ρAl=2700 kg/m3
- Calor específico cAl=880 Jl/(K·kg)
- Sustancia Hierro
- Temperatura inicial T0=100ºC
- Tamaño de la muestra d=10 cm
- Densidad ρx=7880 kg/m3.
- El calor específico del Hierro es
t=0:50:650;
T_Al=[100, 81.4,67.1,56.2,47.7,41.3,36.3,32.5,29.6,27.4,
25.7,24.3,23.3,22.6]-20;
plot(t,log(T_Al),'ro','markersize',4,'markerfacecolor','r');
xlabel('t(s)')
ylabel('log(T)')
grid on
title('Enfriamiento, Aluminio')
En el menú seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla linear en Plot fits. A continuación, pulsamos la flecha hacia la derecha --> para mostrar los coeficientes p1 y p2 del polinomio (recta) y=p1*x+p2 de ajuste.
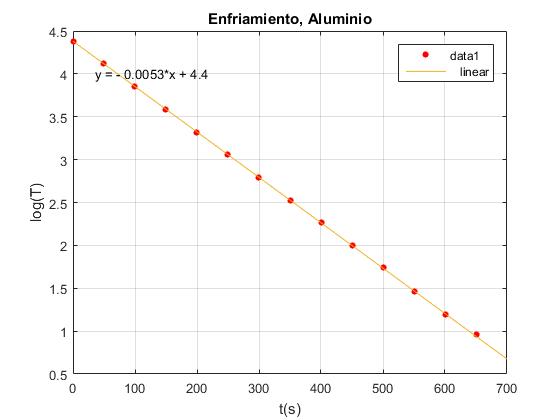
Valor de la pendiente kAl=0.00530
T_Fe=[100,87.0,76.1,67.0,59.3,52.9,47.6,43.1,
39.4,36.2,33.6,31.4,29.5,28.0]-20;
plot(t,log(T_Fe),'ro','markersize',4,'markerfacecolor','r');
xlabel('t(s)')
ylabel('log(T)')
grid on
title('Enfriamiento, Hierro')
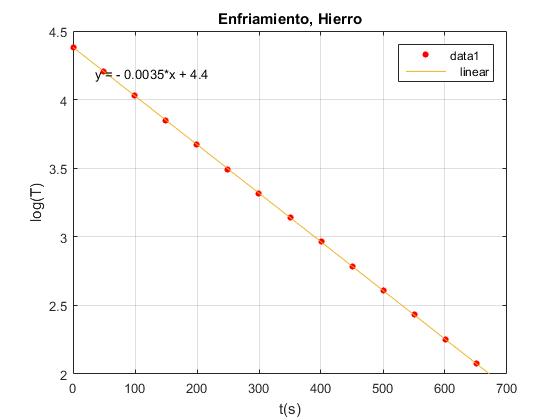
Valor de la pendiente kx=0.00355
Calor específico del hierro
Actividades
En primer lugar, tenemos que elegir el Aluminio como sustancia de referencia en el control titulado Material.
Introducimos los siguientes datos:
- La temperatura inicial T0 (menor de 100ºC) en el control titulado Temperatura.
- El tamaño de la muestra cúbica, la longitud de su lado d en cm, en el titulado Dimensión.
Se pulsa en le botón titulado Nuevo
La temperatura ambiente se ha fijado en el programa interactivo, Ta=20ºC.
En la parte izquierda, se observa un cubo de aluminio y un termómetro que indica su temperatura. En la parte derecha, se observa la evolución de su temperatura T a lo largo del tiempo t. Se toman medidas de la temperatura.
Se representa en el eje vertical ln(T-T0), y en el eje horizontal el tiempo t en s. Se calcula la pendiente kAl de la recta que ajusta a estos datos.
Anotamos el valor de la pendiente, kAl, la densidad del Aluminio ρAl=2700 kg/m3, y el calor específico del Aluminio cAl=880 J/(K·kg)
Tomamos ahora una muestra de otro metal de las mismas dimensiones seleccionándolo en el control de selección titulado Material.
Pulsamos el botón titulado Nuevo.
Observamos la evolución de su temperatura T en función del tiempo t.
La temperatura ambiente cambia con el tiempo
La temperatura ambiente a lo largo de un día cambia con el tiempo. El mínimo se produce de madrugada y el máximo algo más tarde del máximo solar.
En la página web titulada Ajuste de datos a funciones armónicas. Ajustamos la temperatura media medida en los 12 meses del año a la función
x= a0+a1cos(ωt)+a2sin(ωt)
El periodo P=12 meses, la frecuencia angular ω=2π/360 rad/dia.
Disponemos de las medidas de la temperatura ambiente de un laboratorio efectuadas cada medio segundo en el fichero Excel temperatura habitación.xlsx que descargamos y guardamos en la carpeta accesible a MATLAB
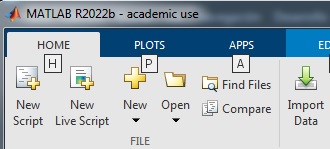
En la pestaña Home pulsamos el botón titulado Import Data, seleccionamos el fichero
Con el puntero del ratón seleccionamos la columna A de los tiempos, excepto la primera fila 1 Tiempo (s). Elegimos en la lista despegable Output Type la segunda opción Column vectors
Pulsamos el botón titulado Import
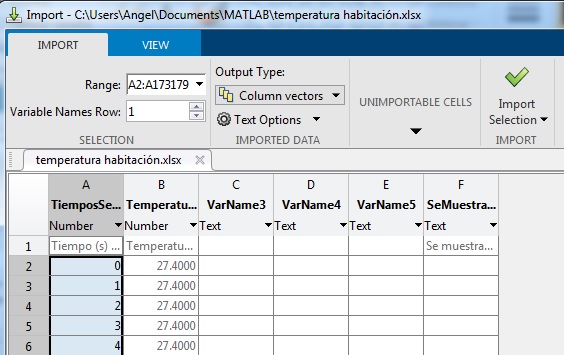
En la ventana Workspace, cambiamos el nombre de la variable por defecto
Repetimos los mismos pasos para importar la columna B de las temperaturas
En la ventana Workspace, cambiamos el nombre de la variable por defecto
Es excesivo procesar 173178 datos por lo que tomamos la temperatura ambiente cada minuto en vez de cada medio segundo. Convertimos los tiempos de segundos a horas
w=2*pi/24;
t=tt(1:120:3600*48)/3600; %dos datos por segundo, tiempo en horas
x=xx(1:120:3600*48);
M=[length(t), sum(cos(w*t)), sum(sin(w*t));
sum(cos(w*t)), sum(cos(w*t).^2), sum(sin(w*t).*cos(w*t));
sum(sin(w*t)),sum(sin(w*t).*cos(w*t)), sum(sin(w*t).^2)];
C=[sum(x);sum(x.*cos(w*t));sum(x.*sin(w*t))];
A=M\C;
disp(A)
hold on
plot(t,x,'bo','markersize',1,'markerfacecolor','b')
f=@(t) A(1)+A(2)*cos(w*t)+A(3)*sin(w*t);
fplot(f,[t(1),t(end)]);
xlabel('hora')
ylabel('temperatura °C')
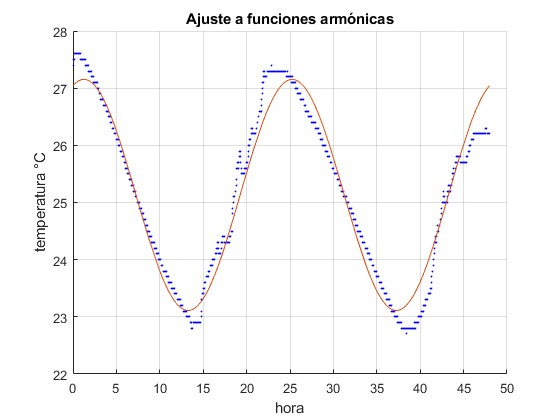
title('Ajuste a funciones armónicas')
grid on
hold off
Los valores obtenidos son a0=25.1322, a1= 1.9133 y a2=0.6516
25.1322
1.9133
0.6516
Los puntos de color azul son las medidas de la temperatura ambiente Ta cada minuto a lo largo de 48 horas, la curva en color rojo es el ajuste a la función
Ta(t)=a0+a1cos(ωt)+a2sin(ωt)
Se coloca la muestra cuya temperatura inicial es T0 en un reciento cuya temperatura Ta cambia con el tiempo de la forma en la que se indica en la figura. Vamos a determinar la temperatura T de la muesta en función del tiempo t, resolviendo la ecuación diferencial
con la condición inicial, en el instante t=0, la temperatura de la muestra es T0
La solución de la ecuación diferencial
es la suma de la solución de la ecuación diferencial homogénea
y de la particular
Introduciendo esta última, en la ecuación diferencial, determinamos los coeficientes A0, A1 y A2
La solución completa es
La constante C se determina sabiendo que en el instante t=0, la temperatura es T0
La temperatura T de la muestra en función del tiempo t es
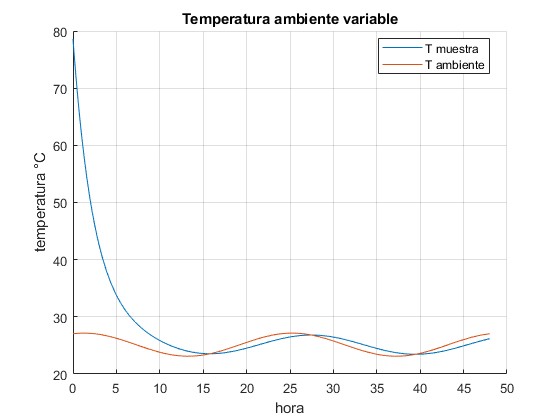
Representamos la temperatura de la muestra T en función del tiempo t para k=0.4 h-1
w=2*pi/24; %frecuencia angular
T0=78.6; %temperatura inicial
k=0.4; %constante k
a0=25.1322; %coeficientes
a1=1.9133;
a2=0.6516;
tf=48; %tiempo final en horas
T=@(t) (T0-a0-k*(k*a1-w*a2)/(k^2+w^2))*exp(-k*t)+a0+k*((k*a1-w*a2)*cos(w*t)+
(w*a1+k*a2)*sin(w*t))/(k^2+w^2);
hold on
fplot(T,[0,tf])
y=@(t) a0+a1*cos(w*t)+a2*sin(w*t);
fplot(y,[0,tf]);
hold off
grid on
legend('T muestra', 'T ambiente','location','best')
xlabel('hora')
ylabel('temperatura °C')
title('Temperatura ambiente variable')
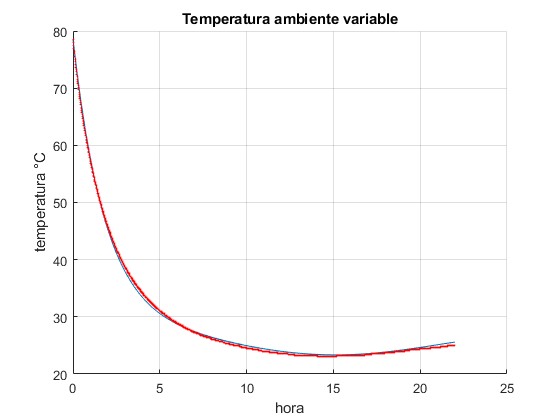
Comparamos con los resultados experimentales contenidos en el fichero experimento ley enfriamiento newton 22 horas .xlsx
Descargamos la columna de tiempos y la columna de temperaturas siguiendo el procedimiento descrito al principio de este apartado. Los tiempos se guardan en el vector
Se observa que la curva teórica (color azul claro) y los datos experimentales (rojo) coinciden para k=0.52 aproximadamente
w=2*pi/24; %frecuencia angular
T0=78.6; %temperatura inicial
k=0.52; %constante k
a0=25.1322; %coeficientes
a1=1.9133;
a2=0.6516;
tf=22; %tiempo final en horas
T=@(t) (T0-a0-k*(k*a1-w*a2)/(k^2+w^2))*exp(-k*t)+a0+k*((k*a1-w*a2)*cos(w*t)+
(w*a1+k*a2)*sin(w*t))/(k^2+w^2);
hold on
fplot(T,[0,tf])
t=tt(1:120:3600*44)/3600; %tiempos
x=te(1:120:3600*44); %temperaturas de la muestra, dos por segundo
plot(t,x,'ro','markersize',1,'markerfacecolor','r')
hold off
grid on
xlabel('hora')
ylabel('temperatura °C')
title('Temperatura ambiente variable')
Referencias
Panayotova S. An undergraduate experiment on thermal properties. Eur. J. Phys. 8 (October 1987) pp. 308-309
P. E. Moreira Galván, O. Ortega Ruíz. Ley de enfriamiento de Newton con temperatura variable. Revista Mexicana de Física E 22 010218 1–6. January–June 2025

