Imaginemos un gas compuesto por N₀ moléculas que ocupan un recipiente a la temperatura T₀. La distribución de equilibrio es

${\displaystyle dn=\frac{2N_0}{\sqrt{\pi }{\left(k{T}_0\right)}^{3/2}}{E}^{1/2}\exp \left(\frac{-E}{k{T}_0}\right)dE}$

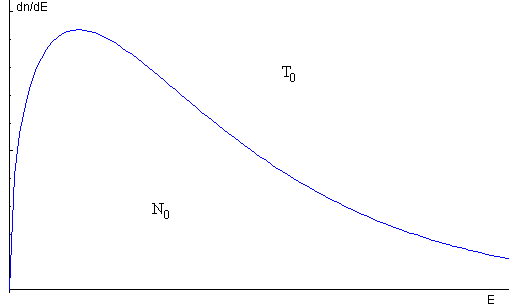
Por algún procedimiento (véase el artículo citado en las referencias) se retiran del recipiente todas las moléculas que se muevan con una velocidad superior a v_c o tengan una energía superior a E_c (en color azul en la figura) quedando N₁ moléculas en el recipiente.

${\displaystyle N_1=\frac{2N_0}{\sqrt{\pi }{\left(k{T}_0\right)}^{3/2}}{\displaystyle \underset{0}{\overset{E_c}{\int }}{E}^{1/2}\exp \left(\frac{-E}{k{T}_0}\right)dE}}$

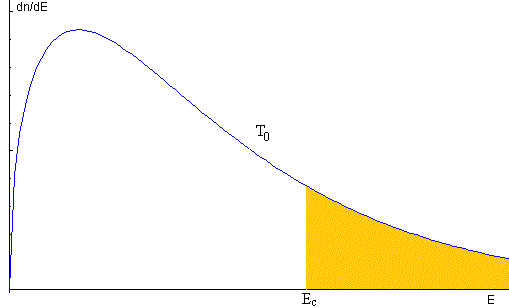
Las N₁ moléculas que permanecen en el recipiente están inicialmente en una situación de no equilibrio tal como se muestra en la figura, más abajo

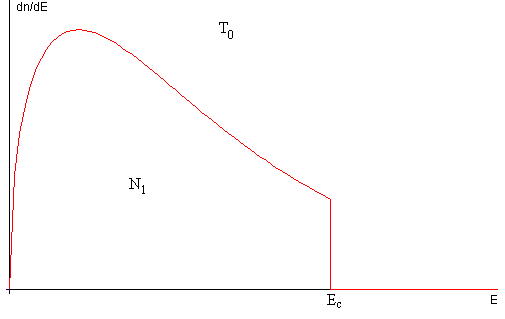
Las N₁ moléculas que permanecen en el recipiente chocan entre sí y vuelven a adoptar la distribución de equilibrio a una temperatura inferior T₁

${\displaystyle dn=\frac{2N_1}{\sqrt{\pi }{\left(k{T}_1\right)}^{3/2}}{E}^{1/2}\exp \left(\frac{-E}{k{T}_1}\right)dE}$

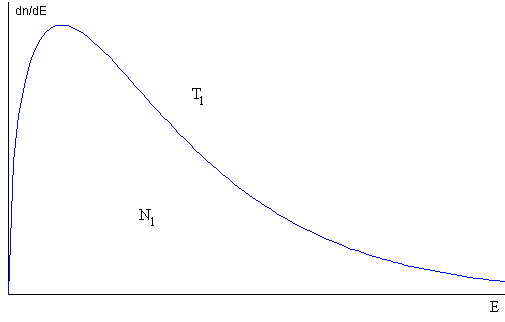
La energía antes y después alcanzar la distribución de equilibrio no cambia, de modo que

${\displaystyle \frac{2N_0}{\sqrt{\pi }{\left(k{T}_0\right)}^{3/2}}{\displaystyle \underset{0}{\overset{E_c}{\int }}{E}^{3/2}\exp \left(\frac{-E}{k{T}_0}\right)dE}=\frac{2N_1}{\sqrt{\pi }{\left(k{T}_1\right)}^{3/2}}{\displaystyle \underset{0}{\overset{\infty }{\int }}{E}^{3/2}\exp \left(\frac{-E}{k{T}_1}\right)dE}}$

Dada la energía E_c, calculamos la temperatura T₁ de las N₁ moléculas del gas que permenecen en el recipiente.

En la página anterior hemos calculado la integral de la derecha, para obtener la energía interna U de N moléculas de un gas a la temperatura T

${\displaystyle \frac{2N_1}{\sqrt{\pi }{\left(k{T}_1\right)}^{3/2}}{\displaystyle \underset{0}{\overset{\infty }{\int }}{E}^{3/2}\exp \left(\frac{-E}{k{T}_1}\right)dE}=\frac{3}{2}{N}_{1}k{T}_1}$

Sustituimos N₁ y despejamos T₁

${\displaystyle \begin{array}{l}\frac{2N_0}{\sqrt{\pi }{\left(k{T}_0\right)}^{3/2}}{\displaystyle \underset{0}{\overset{E_c}{\int }}{E}^{3/2}\exp \left(\frac{-E}{k{T}_0}\right)dE}=\frac{3}{2}k{T}_1\frac{2N_0}{\sqrt{\pi }{\left(k{T}_0\right)}^{3/2}}{\displaystyle \underset{0}{\overset{E_c}{\int }}{E}^{1/2}\exp \left(\frac{-E}{k{T}_0}\right)dE}\\ T_1=\frac{2{\displaystyle \underset{0}{\overset{E_c}{\int }}{E}^{3/2}\exp \left(\frac{-E}{k{T}_0}\right)dE}}{3k{\displaystyle \underset{0}{\overset{E_c}{\int }}{E}^{1/2}\exp \left(\frac{-E}{k{T}_0}\right)dE}}\end{array}}$

Hacemos el cambio de variable  x=E/kT

El número de partículas que permanece en el recipiente es

${\displaystyle N_1=\frac{2N}{\sqrt{\pi }}{\displaystyle \underset{0}{\overset{xc}{\int }}{x}^{1/2}\exp (-x)dx}}$

La temperatura T₁ del gas compuesto por N₁ moléculas es

${\displaystyle T_1=T_0\frac{2{\displaystyle \underset{0}{\overset{x_c}{\int }}{x}^{3/2}\exp (-x)dx}}{3{\displaystyle \underset{0}{\overset{x_c}{\int }}{x}^{1/2}\exp (-x)dx}}}$

Tomando T₀=300 K y E_c=0.06 eV, entonces x_c=2.32

>> syms x xc;
>> y=x^(3/2)*exp(-x);
>> num=int(y,0,xc);
>> y=x^(1/2)*exp(-x);
>> den=int(y,0,xc);
>> t1=2*num/(3*den);
>> subs(t1,xc,2.32)*300
ans =  202.0198

Resolvemos la integral del denominador

${\displaystyle {\displaystyle \underset{0}{\overset{xc}{\int }}{x}^{1/2}\exp (-x)dx}}$

Se hace el cambio de variable y²=x

${\displaystyle 2{\displaystyle \underset{0}{\overset{\sqrt{x_c}}{\int }}{y}^2\exp (-y^2)dy}}$

Se integra por partes

${\displaystyle \begin{array}{l}2{\left(-\frac{1}{2}y\exp (-y^2)+\frac{1}{2}{\displaystyle \int \exp (-y^2)dy}\right)}_0^{\sqrt{x_c}}=\\ \left(-\sqrt{x_c}\exp (-x_c)+\frac{\sqrt{\pi }}{2}\text{erf}\left(\sqrt{x_c}\right)\right)\end{array}}$

>> syms x xc;
>> int('x^(1/2)*exp(-x)',x,0,xc)
ans =(pi^(1/2)*erf(xc^(1/2)))/2 - xc^(1/2)*exp(-xc)

Resolvemos la integral del numerador

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{xc}{\int }}{x}^{3/2}\exp (-x)dx}=2{\displaystyle \underset{0}{\overset{\sqrt{x_c}}{\int }}{y}^4\exp (-y^2)dy}=\\ 2{\left(-\frac{1}{2}{y}^3\exp (-y^2)+\frac{3}{2}{\displaystyle \int y^2\exp (-y^2)dy}\right)}_0^{\sqrt{x_c}}=\\ {\left(-y^3\exp (-y^2)-\frac{3}{2}y\exp (-y^2)+\frac{3}{2}{\displaystyle \int \exp (-y^2)dy}\right)}_0^{\sqrt{x_c}}=\\ \frac{3\sqrt{\pi }}{4}\text{erf}\left(\sqrt{x_c}\right)-\sqrt{x_c}\left(x_c+\frac{3}{2}\right)\exp (-x_c)\end{array}}$

>> syms x xc;
>> int('x^(3/2)*exp(-x)',x,0,xc)
ans = 
(3*pi^(1/2)*(erf(xc^(1/2)) - 1))/4 + (3*pi^(1/2))/4 - 
(xc^(1/2)*exp(-xc)*(2*xc + 3))/2

La temperatura T₁ es

${\displaystyle T_1=\frac{T_0\left(3\sqrt{\pi }\text{erf}\left(\sqrt{x_c}\right)-\left(4x_c\sqrt{x_c}+6\sqrt{x_c}\right)\exp (-x_c)\right)}{3\left(\sqrt{\pi }\text{erf}\left(\sqrt{x_c}\right)-2\sqrt{x_c}\exp (-x_c)\right)}}$

>> xc=2.32;
>> T1=300*(erf(sqrt(xc))*3*sqrt(pi)/2-(2*xc^1.5+3*sqrt(xc))*exp(-xc))...
/(erf(sqrt(xc))*3*sqrt(pi)/2-3*sqrt(xc)*exp(-xc))
T1 =  202.0198

El número de moléculas

${\displaystyle N_1=N_0\left(\text{erf}\left(\sqrt{x_c}\right)-\frac{2}{\sqrt{\pi }}\sqrt{x_c}\exp (-x_c)\right)}$

Establecemos la temperatura inicial del gas T₀

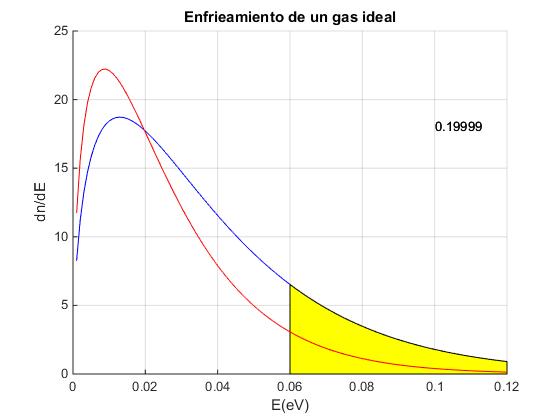
Se representa la función de distribución de las moléculas dn/dE con la energía E expresada en electrón-voltios eV

Establecemos la energía E_c de corte o mínima de las moléculas que se van a eliminar del recipiente

La proporción de moléculas que van a ser eliminadas, es el cociente entre el área bajo la curva de la distribución señalada en color amarillo y el área total bajo la curva.

Se proporciona el dato de la proporción de moléculas eliminadas en la parte superior derecha de la imagen.

La distribución inicial de no equilibrio, se convierte en una distribución de equilibrio a una temperatura inferior, debido a los choques entre las molécula del gas contenido en el recipiente.

Se proporciona el dato de la nueva temperatura T₁ y de la proporción de moléculas que permanecen en el recipiente, N₁/N₀.

Se compara la distribución de equilibrio a la temperatura T₀ (en color azul) con la distribución actual a la temperatura T₁ (en color rojo).

El estado final es el estado inicial para una nueva iteracción. Se establece una nueva energía de corte E_c (o se mantiene el mismo valor). De este modo, vamos enfriando el gas a la vez que van eliminando las moléculas más energéticas del mismo.

T0=300; %temperatura inicial
Ec=0.06; %energía de corte en eV
N0=1;
xc=Ec*11604.49/T0;
T1=T0*(3*sqrt(pi)*erf(sqrt(xc))-(4*xc*sqrt(xc)+
6*sqrt(xc))*exp(-xc))/(3*(sqrt(pi)*erf(sqrt(xc))-2*sqrt(xc)*exp(-xc)));
N1=N0*(erf(sqrt(xc))-2*sqrt(xc)*exp(-xc)/sqrt(pi));
fprintf('Temperatura: %3.1f, permanecen %1.3f\n',T1,N1);

T=T0;
N=N0;
pr=1-2*(sqrt(pi)*erf(sqrt(xc))/2-sqrt(xc)*exp(-xc))/sqrt(pi); %proporción
%distribución de equilibrio a la temparatura T0
f=@(x) 2*N*sqrt(x).*exp(-11604.49*x/T)*1250083.9/(sqrt(pi)*T^(3/2));
E=(0.1:0.1:12)/100;
y=f(E);
hold on
plot(E,y, 'b')
%se eliminan las moléculas cuya energía E>Ec, señaladas en la gráfica
xx=[Ec Ec E(E>Ec & E<0.12) 0.12 0.12];
yy=[0 f(Ec) y(E>Ec & E<0.12) f(0.12) 0];
fill(xx,yy,'y'); %rellena un área de color especificado
text(0.1,18,num2str(pr));

T=T1; 
N=N1;
%distribución de equilibrio a la temparatura T1
f=@(x) 2*N*sqrt(x).*exp(-11604.49*x/T)*1250083.9/(sqrt(pi)*T^(3/2));
y=f(E);
plot(E,y, 'r')

hold off
grid on
xlabel('E(eV)')
ylabel('dn/dE')
title('Enfriamiento de un gas ideal')

Temperatura: 202.1, permanecen 0.800

Referencias

Henn E. A., Seman J. A., Ramos E. R. F., Iavaronni A. H., Amthor T., Bagnato V. S., Evaporation in atomic traps: A simple approach. Am. J. Phys. 75 (10) October 2007, pp. 907-910