Sea un recipiente cilíndrico de sección S, perfectamente aislado, en posición vertical con un émbolo que separa una parte que está vacía a presión p=0 y la otra parte que contiene un gas.

Si en un momento dado la temperatura absoluta del gas es T y la altura del émbolo es y. La ecuación de los gases ideales, nos relaciona la presión p, el volumen y·S y la temperatura T de una masa de gas o de su número n de moles.

p·S·y =nRT
f·y =nRT

Donde f es la fuerza que ejerce el gas sobre el émbolo debido a la presión

R=8.3143 J/(K·mol) es la constante de los gases

La energía del gas ideal es

${\displaystyle U=n{c}_{v}T=\frac{pS·y}{RT}\frac{R}{\gamma -1}T=\frac{f·y}{\gamma -1}}$

El índice γ=5/3 para un gas monoatómico y γ=7/5 para un gas diatómico

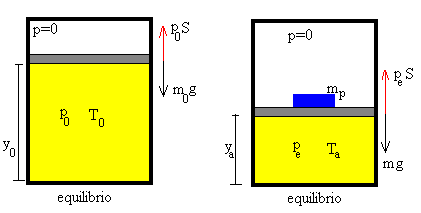
Efectuamos una transformación adiabática entre el estado inicial de equilibrio caracterizado por

• Una presión p₀ o la fuerza sobre el émbolo f₀=p₀/S debida a la presión del gas f₀=m₀g

• Un volumen V₀₌y₀·S o altura del émbolo y₀.

• Una temperatura, T₀

• una energía inicial

${\displaystyle U_0=\frac{m_{0}g{y}_0}{\gamma -1}}$

Un estado final de equilibrio caracterizado por

• Una presión p_e o la fuerza sobre el émbolo f_e=p_e/S debida a la presión del gas f_e=(m₀+m_p)g=mg

• Un volumen V_a=y_a·S o altura del émbolo y_a.

• Una temperatura T_a

La altura y_a del émbolo se calcula a partir de la ecuación de la transformación adiabática

${\displaystyle f_0{y}_0^{\gamma }=f_e{y}_a^{\gamma }}$

La temperatura T_a a partir de la ecuación de los gases ideales

${\displaystyle \frac{(m_0+m_p)·y_a}{T_a}=\frac{m_0{y}_0}{T_0}}$

Proceso de un solo paso

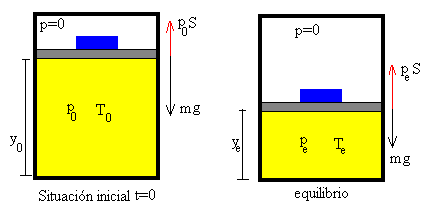
Un bloque de masa m_p se coloca sobre el émbolo de masa m₀ en la posición inicial y₀ con velocidad inicial cero y llega a su posición final de equilibrio y_e con velocidad nula.

La ecuación del balance energético, es

${\displaystyle \frac{m_{0}g{y}_0}{\gamma -1}+mg{y}_0=mgy+\frac{1}{2}m{v}^2+\frac{f·y}{\gamma -1}}$

En el miembro izquierdo, tenemos la energía inicial (interna del gas y potencial del conjunto bloque-émbolo), a la derecha la energía cinética y potencial del conjunto bloque-émbolo y la energía interna final del gas.

El émbolo llega a la posición de equilibrio estable y=y_e después de cierto tiempo. En esta posición de equilibrio, la fuerza f que ejerce el gas sobre el émbolo debida a la presión se anula con el peso del conjunto formado por el bloque y el émbolo f=mg en

${\displaystyle \frac{m_{0}g{y}_0}{\gamma -1}+mg{y}_0=mg{y}_e+\frac{mg·y_e}{\gamma -1}}$

La energía potencial del conjunto émbolo-bloque correspondiente a la altura (y₀-y_e) se convierte enteramente en energía interna del gas en la posición final de equilibrio y_e.

ΔE_p=(m₀+m_p)g(y₀-y_e)

Despejamos la posición final de equilibrio y_e de la ecuación de la conservación de la energía,

${\displaystyle y_e-y_0=-\frac{m_p}{m_0+m_p}\frac{y_0}{\gamma }}$

La temperatura en el estado final de equilibrio, se obtiene a partir de la ecuación de los gases ideales

${\displaystyle \frac{(m_0+m_p)·y_e}{T_e}=\frac{m_0{y}_0}{T_0}}$

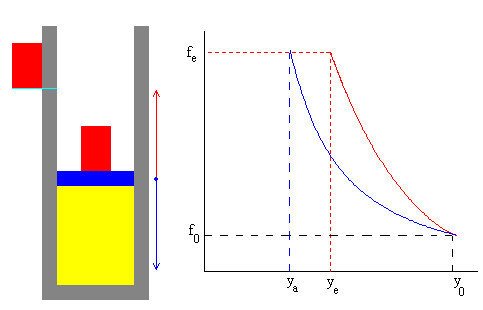
Comparando la transformación adiabática y el proceso de un solo paso, vemos que el estado final tiene la misma presión, pero distintos volúmenes y por tanto, distinta temperatura, tal como puede apreciarse en la figura.

• La curva de color azul representa la transformación adiabática reversible

• La curva en color rojo, el proceso de un solo paso.

Proceso de N pasos

Nos aproximaremos al proceso reversible a través de una transformación consistente en una sucesión de N estados de equilibrio que nos conducirán desde el estado inicial al final. Para ello, dividimos el bloque de masa m_p en N trozos iguales, que se colocan sucesivamente sobre el émbolo cada vez que se alcanza el equilibrio.

Un proceso irreversible trascurre durante un determinado tiempo, mientras que una transformación consistente en una sucesión de estados de equilibrio puede tener una duración ilimitada.

Dividimos el bloque en N trozos iguales de masa Δm=m_p/N, donde m_p es la masa del bloque y los vamos colocando sobre el émbolo del siguiente modo:

• Situación inicial

Partimos de la situación inicial de equilibrio, con el émbolo a una altura y₀. La fuerza que ejerce el gas f₀ sobre el émbolo debida a la presión se compensa con el peso del émbolo m₀g.

• Primera etapa

Colocamos un trozo del bloque de masa Δm, observamos que comprime el gas y alcanza la posición de equilibrio y₁ a la altura.

${\displaystyle y_1-y_0=\frac{-\Delta m}{m_0+\Delta m}\frac{y_0}{\gamma }}$

La fuerza f₁ que ejerce el gas debido a la presión, se iguala al peso del conjunto formado por el émbolo y la porción del bloque, f₁=(m₀+ Δm)g

• Segunda etapa

La posición de equilibrio y₁ es ahora la posición inicial cuando se coloca el segundo trozo del bloque de igual masa Δm. Observamos que se comprime el gas y alcanza la posición de equilibrio y₂ a la altura.

${\displaystyle y_2-y_1=\frac{-\Delta m}{m_0+2\Delta m}\frac{y_1}{\gamma }}$

La fuerza f₂ que ejerce el gas debido a la presión, se iguala al peso del conjunto formado por el émbolo y la porción del bloque, f₂=(m₀+ 2Δm)g

• Etapa N

La posición de equilibrio y_N-1 es la posición inicial cuando se coloca la última porción N de bloque. Observamos que se comprime el gas y alcanza la posición de equilibrio final y_N a la altura.

${\displaystyle y_N-y_{N-1}=\frac{-\Delta m}{m_0+N\Delta m}\frac{y_{N-1}}{\gamma }}$

La fuerza f_N que ejerce el gas debido a la presión, se iguala al peso del conjunto formado por el émbolo y la porción del bloque, f_N=(m₀+NΔm)g

Balance energético

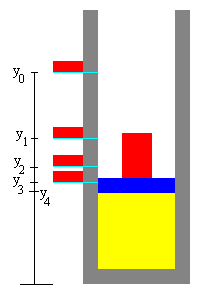
Se coloca la primera porción de bloque de masa Δm en la posición de partida y₀, se alcanza el equilibrio en la posición y₁.

Se coloca la segunda porción de bloque en la posición y₁, se alcanza el equilibrio en la posición y₂.

Se coloca la tercera porción de bloque en la posición y₂, se alcanza el equilibrio en la posición y₃.

Y así, sucesivamente... El proceso consta de una sucesión de N estados de equilibrio

La energía potencial del conjunto formado por el émbolo y de las porciones del bloque que se van colocando sucesivamente sobre el émbolo, se convierte enteramente en energía interna del gas en la posición final de equilibrio y_N. El principio de conservación de la energía se escribe

${\displaystyle \frac{m_{0}g{y}_0}{\gamma -1}+\Delta E_p=\frac{(m_0+N·\Delta m)g·y_N}{\gamma -1}}$

La variación de energía potencial vale (véase la figura)

ΔE_p= (m₀+Δm)·g·(y₀-y₁)+ (m₀+2Δm)·g·(y₁-y₂)+ …+(m₀+NΔm)·g·(y_N-1-y_N)

${\displaystyle \Delta E_p=\frac{\Delta m}{\gamma }g{\displaystyle \sum _{i=0}^{N-1}{y}_i}}$

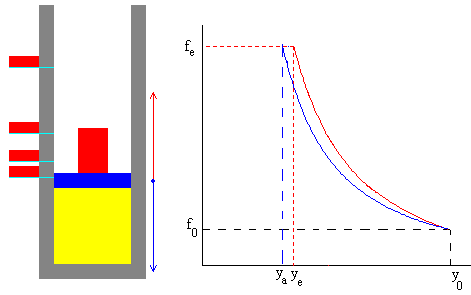
Comparando el proceso reversible y la transformación consistente en una sucesión estados de equilibrio vemos que el estado final tiene la misma presión, pero distintos volúmenes y por tanto, distinta temperatura, tal como puede apreciarse en la figura.

• La curva de color azul representa la transformación adiabática

• La curva en color rojo, la sucesión de estados de equilibrio.

Cuanto mayor sea el número de porciones N, en el que se divide el bloque, mayor es el grado de ajuste con el proceso reversible, que conecta los estados inicial y final.

En la parte derecha, se dibujan las fuerzas sobre el émbolo:

• El peso del conjunto formado por el bloque-émbolo (flecha azul)

• La fuerza que ejerce la presión del gas sobre el émbolo (flecha roja)

El proceso es una sucesión de N estados de equilibrio. Cuando N es grande, observamos que hay muy poca diferencia entre las dos fuerzas que actúan sobre el émbolo a lo largo de todo el proceso. Naturalmente, en las posiciones de equilibrio son iguales.

De la formulación discreta a la continua

La diferencia entre dos posiciones consecutivas de equilibrio estable, se escribe

${\displaystyle \frac{y_N-y_{N-1}}{y_{N-1}}=\frac{-1}{\gamma }\frac{\Delta m}{m_0+N·\Delta m}}$

Cuando pasamos del límite discreto al continuo

${\displaystyle \frac{dy}{y}=-\frac{1}{\gamma }\frac{dm}{m_0+m}}$

Integrando miembro a miembro

${\displaystyle \gamma \ln y=-\ln (m_0+m)+\text{cte}}$

O bien

${\displaystyle (m_0+m)y^{\gamma }=\text{cte}}$

En un proceso reversible todas las posiciones del émbolo son de equilibrio, por lo que se cumple f=(m₀+m)g cuando el émbolo está a una altura y, y f₀=m₀g en la posición inicial cuando la altura del émbolo es y₀.

${\displaystyle f{y}^{\gamma }=f_0{y}_0^{\gamma }}$

Esta es la ecuación de una transformación adiabática.

Balance energético

Para n trozos la variación de energía potencial es

${\displaystyle \Delta E_p=\frac{\Delta m}{\gamma }g{\displaystyle \sum _{i=0}^{N-1}{y}_i}}$

La variación de energía potencial se escribe para el límite continuo

${\displaystyle \Delta E_p=\frac{g}{\gamma }{\displaystyle \underset{y_0}{\overset{y_e}{\int }}y·dm}}$

Para integrar respecto de la variable y, utilizamos la relación entre y y la masa m del bloque

${\displaystyle \begin{array}{l}(m_0+m)y^{\gamma }=m_0{y}_0^{\gamma }dm=-\gamma \frac{m_0{y}_0^{\gamma }}{y^{\gamma +1}}dy\\ \Delta E_p=-g{m}_0{y}_0^{\gamma }{\displaystyle \underset{y_0}{\overset{y_e}{\int }}\frac{dy}{y^{\gamma }}}=\frac{g{m}_0}{\gamma -1}\left(y_0^{\gamma }{y}_e^{-\gamma +1}-y_0\right)\end{array}}$

Comprobamos que se cumple la ecuación de la conservación de la energía para el límite continuo

${\displaystyle \frac{m_{0}g{y}_0}{\gamma -1}+\Delta E_p=\frac{(m_0+m)g·y}{\gamma -1}}$

Actividades

Se introduce

• El tipo de gas, monoatómico o diatómico, activando el botón de radio correspondiente.

• La temperatura inicial T₀ del gas encerrado en el recipiente, en el control titulado Temperatura

• La masa del émbolo m₀ se ha fijado en un kg.

• La masa del bloque m_p se ha fijado en 5 kg

• El número de moles se ha fijado en n=0.002 mol

Se pulsa el botón titulado Nuevo.

Se observa el estado inicial de equilibrio, el émbolo está en la posición y₀.

• Se introduce el número N de trozos en el que se ha dividido en bloque de 5 kg, en el control titulado Número de trozos

Se pulsa el botón titulado Nuevo

Se pone el bloque de masa m_p sobre el émbolo y observamos su movimiento

Se representan las fuerzas sobre el conjunto émbolo-bloque,

• El peso (m₀+m_p)g=mg

• La fuerza f que ejerce el gas sobre el émbolo debida a la presión

y se proporciona el dato de la resultante f-mg.

Se proporcionan los datos del tiempo y velocidad de émbolo en la parte superior derecha, la temperatura (en kelvin) en la parte inferior del recipiente.

En la parte derecha, se representa la fuerza f que ejerce el gas sobre el émbolo en función de la altura y del émbolo. Se compara con la curva (de color azul) que es la representación de la transformación adiabática f·y^γ=cte. La constante se determina conociendo la fuerza f₀ (presión) y el desplazamiento y₀ (volumen) en el instante t=0.

Ejemplo:

Se introduce

• La temperatura 20ºC=293 K

• Se selecciona gas monoatómico

Se pulsa el botón titulado Nuevo

Estado inicial

En el estado inicial de equilibrio, la fuerza que ejerce el gas sobre el émbolo es igual al peso del émbolo

f₀=p₀·S= m₀g=1·9.8 N

Conociendo el número n=0.002 de moles de gas y su temperatura T₀=293 K calculamos el volumen o la posición inicial y₀ del émbolo, aplicando la ecuación de los gases perfectos, p₀·V₀=nRT₀

${\displaystyle m_{0}g·y_0=nR{T}_0{y}_0=\frac{0.002·8.3143·293}{1·9.8}=0.497\text{m}=\text{49}\text{.7}\text{cm}}$

Proceso de un solo paso

Se introduce Número de trozos N=1, se coloca el bloque entero sobre el émbolo en la situación inicial

Se pulsa el botón titulado Nuevo.

El émbolo desciende y comprime el gas, hasta que detiene en la posición de equilibrio. El peso del conjunto bloque-émbolo (m₀+m_p)g se igualan a la fuerza f_e que ejerce el gas sobre el émbolo debido a la presión.

f_e=(1+5)·9.8 =58.8 N

Como toda la energía potencial del conjunto bloque-émbolo se convierte en energía interna del gas, la posición final de equilibrio se obtiene

${\displaystyle y_1-y_0=\frac{-m_p}{m_0+m_p}\frac{y_0}{\gamma }{y}_1=0.497-\frac{5}{1+5}\frac{0.497}{\frac{5}{3}}=0.248\text{m}}$

Calculamos ahora, la temperatura en esta situación de equilibrio

${\displaystyle \frac{(m_0+m_p)·y_1}{T_1}=\frac{m_0{y}_0}{T_0}\frac{6·0.248}{T_1}=\frac{1·0.497}{293}}$

T₁=879.0 K

La energía potencial que se transforma en energía interna es la que corresponde a la altura y₀-y₁

ΔE_p=(m₀+m_p)g(y₀-y₁) =6·9.8·(0.497-0.248)=14.61 J

Proceso de N pasos

Partimos del estado inicial del ejemplo anterior

• Se introduce el número de trozos iguales en el que se ha dividido el bloque, por ejemplo N=4.

Se pone sobre el émbolo una masa Δm=5/4=1.25 kg, en la situación inicial de partida

Se pulsa el botón titulado Nuevo.

1. Primera etapa

El émbolo desciende y comprime el gas, hasta que se detiene su movimiento en la posición de equilibrio. El peso del conjunto bloque-émbolo (m₀+Δm)g se iguala a la fuerza f₁ que ejerce el gas sobre el émbolo debido a la presión.

f₁=(1+1.25)·9.8 =22.05 N

Como toda la energía potencial del conjunto bloque-émbolo se convierte en energía interna del gas, la posición final de equilibrio se obtiene

${\displaystyle y_1-y_0=\frac{-\Delta m}{m_0+\Delta m}\frac{y_0}{\gamma }{y}_1=0.497-\frac{1.25}{1+1.25}\frac{0.497}{\frac{5}{3}}=0.331\text{m}}$

Calculamos la temperatura en esta situación de equilibrio

${\displaystyle \frac{(m_0+\Delta m)·y_1}{T_1}=\frac{m_0{y}_0}{T_0}\frac{2.25·0.331}{T_1}=\frac{1·0.497}{293}}$

T₁=439.5 K

2. Segunda etapa

El émbolo con los dos trozos encima se mueve hacia la nueva posición de equilibrio y₂

${\displaystyle y_2-y_1=\frac{-\Delta m}{m_0+2\Delta m}\frac{y_1}{\gamma }{y}_2=0.331-\frac{1.25}{1+2.5}\frac{0.331}{\frac{5}{3}}=0.260\text{m}}$

Calculamos la temperatura en esta situación de equilibrio

${\displaystyle \frac{(m_0+2\Delta m)·y_2}{T_2}=\frac{m_0{y}_0}{T_0}\frac{3.5·0.260}{T_2}=\frac{1·0.497}{293}}$

T₂=537.2 K

3. Tercera etapa

El émbolo con los tres trozos encima se mueve hacia la nueva posición de equilibrio y₂

${\displaystyle y_3-y_2=\frac{-\Delta m}{m_0+3\Delta m}\frac{y_2}{\gamma }{y}_2=0.260-\frac{1.25}{1+3.75}\frac{0.260}{\frac{5}{3}}=0.219\text{m}}$

Calculamos la temperatura en esta situación de equilibrio

${\displaystyle \frac{(m_0+3\Delta m)·y_3}{T_3}=\frac{m_0{y}_0}{T_0}\frac{4.75·0.219}{T_3}=\frac{1·0.497}{293}}$

T₃=613.9 K

4. Cuarta etapa

El émbolo con los tres trozos encima se mueve hacia la nueva posición de equilibrio y₂

${\displaystyle y_4-y_3=\frac{-\Delta m}{m_0+4\Delta m}\frac{y_3}{\gamma }{y}_4=0.219-\frac{1.25}{1+5}\frac{0.219}{\frac{5}{3}}=0.192\text{m}}$

Calculamos la temperatura en esta situación de equilibrio

${\displaystyle \frac{(m_0+4\Delta m)·y_4}{T_4}=\frac{m_0{y}_0}{T_0}\frac{6·0.192}{T_4}=\frac{1·0.497}{293}}$

T₄=678.5 K

5. Balance energético

La variación de energía potencial que se transforma en energía interna es

ΔE_p= (m₀+Δm)·g·(y₀-y₁)+ (m₀+2Δm)·g·(y₁-y₂)+ (m₀+3Δm)·g·(y₂-y₃)+ (m₀+4Δm)·g·(y₃-y₄)=9.61 J

Esto explica que la temperatura final del gas sea menor. La variación de energía potencial entre la posición inicial y₀ y la posición final y₄ se puede escribir

${\displaystyle \begin{array}{l}\Delta E_p=\frac{\Delta m}{\gamma }g\left(y_0+y_1+y_2+y_3\right)=\\ \frac{1.25}{5/3}·9.8·\left(0.497+0.331+0.260+0.219\right)=9.61\text{J}\end{array}}$

Proceso reversible

Una transformación adiabática entre el estado inicial f₀=m₀g, y₀, y el estado final caracterizado por una fuerza debida a la presión f_e=mg=(m₀+m_p)g, es

${\displaystyle \begin{array}{l}{f}_0{y}_0^{\gamma }=f_e{y}_e^{\gamma }{y}_e={\left(\frac{1·9.8}{6·9.8}\right)}^{\frac{3}{5}}0.497=0.169\text{m}\\ \frac{(m_0+m_p)·y_e}{T_e}=\frac{m_0{y}_0}{T_0}\frac{6·0.169}{T_e}=\frac{1·0.497}{293}\end{array}}$

T_e=600.0 K

Comparación de resultados

Estado final de equilibrio

Hay diferencia entre el proceso reversible y una transformación consistente en cuatro pasos, pero la diferencia ha disminuido notablemente respecto de la transformación que consta de un solo paso.

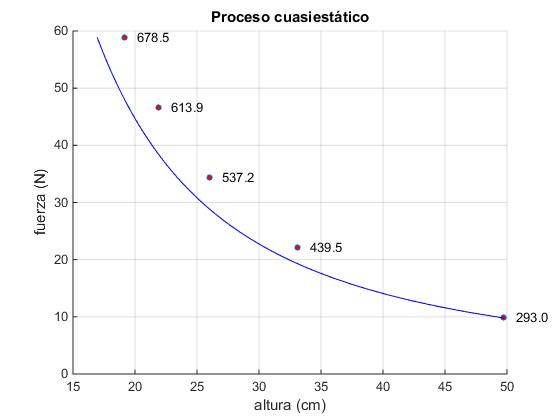
Elaboramos un script para realizar la representación gráfica de la transformación adiabática, entre el estado inicial (y₀, m₀g) y el estado final (y_e, (m₀+m_p)g), junto a la representación gráfica de los estados de equilibrio del final de cada una de las N etapas, (y_j, (m₀+j·dm)g) en las que se ha dividido el proceso

gamma=5/3;  %gas monoatómico, 7/5 para un gas diatómico
nMoles=0.002; %moles de gas
m0=1; %masa del émbolo
mp=5; %masa del bloque en trozos, completo
N=4; %número de trozos en lo que se divide el bloque
dm=mp/N; %masa de cada trozo
y=zeros(N+1,1);
f=zeros(N+1,1);
T=zeros(N+1,1);
%situación inicial
T(1)=293; %temperatura inicial
f(1)=m0*9.8;
y(1)=nMoles*8.3143*T(1)/f(1);
%estado de equilibrio al final de cada etapa
for j=1:N
    y(j+1)=y(j)-dm*y(j)/((m0+j*dm)*gamma);
    f(j+1)=(m0+mp*j/N)*9.8;
    T(j+1)=f(j+1)*y(j+1)*T(1)/(f(1)*y(1));
end
%transformación adiabática
fp=linspace(m0*9.8,(m0+mp)*9.8,50);
yp=((f(1)*y(1)^gamma)./fp).^(1/gamma);
hold on
plot(y*100,f,'o','markersize',4,'markerfacecolor','r')
for j=1:N+1
    text(y(j)*100+1,f(j),sprintf('%3.1f',T(j))) %temperatura
end

plot(yp*100,fp,'b')
grid on
hold off
ylabel('fuerza (N)')
xlabel('altura (cm)')
title('Proceso cuasiestático')