Convección

Hay de dos tipos de convección:

• Natural
• Forzada

La natural es complicada de describir ya que depende de la geometría de los cuerpos que intervienen y de las características del fluido (aire) transmisor del calor y de su movimiento (laminar, turbulento).

${\displaystyle \frac{dQ}{dt}\propto {\left(T-T_a\right)}^n}$

Donde n=5/4 para el caso de flujo laminar y n=4/3 para el caso de flujo turbulento.
En cuanto a la convección forzada, por ejemplo, una corriente de aire que fluye sobre el cuerpo, está bastante bien descrita por la ley del enfriamiento de Newton n=1.

Absorción y emisión de la radiación por un cuerpo

El término radiación se refiere a la emisión continua de energía desde la superficie de cualquier cuerpo, esta energía se denomina radiante y es transportada por las ondas electromagnéticas que viajan en el vacío a la velocidad de 3·10⁸ m/s. Las ondas de radio, las radiaciones infrarrojas, la luz visible, la luz ultravioleta, los rayos X y los rayos gamma, constituyen las distintas regiones del espectro electromagnético.

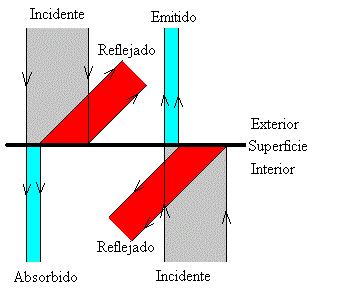
Sobre la superficie de un cuerpo incide constantemente energía radiante, tanto desde el interior como desde el exterior, la que incide desde el exterior procede de los objetos que rodean al cuerpo. Cuando la energía radiante incide sobre la superficie una parte se refleja y la otra parte se transmite.

Consideremos la energía radiante que incide desde el exterior sobre la superficie del cuerpo. Si la superficie es lisa y pulimentada, como la de un espejo, la mayor parte de la energía incidente se refleja, el resto atraviesa la superficie del cuerpo y es absorbido por sus átomos o moléculas.

Si r es la proporción de energía radiante que se refleja, y a la proporción que se absorbe, se debe de cumplir que r+a=1.

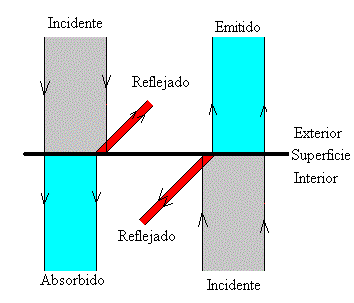
La misma proporción r de la energía radiante que incide desde el interior se refleja hacia dentro y se transmite la proporción a=1-r que se propaga hacia afuera y se denomina por tanto, energía radiante emitida por la superficie.

En la figura, se muestra el comportamiento de la superficie de un cuerpo que refleja una pequeña parte de la energía incidente. Las anchuras de las distintas bandas corresponden a cantidades relativas de energía radiante incidente, reflejada y transmitida a través de la superficie.

Comparando ambas figuras, vemos que un buen absorbedor de radiación es un buen emisor, y un mal absorbedor es un mal emisor. También podemos decir, que un buen reflector es un mal emisor y un mal reflector es un buen emisor.

Una aplicación práctica está en los termos utilizados para mantener la temperatura de los líquidos como el café. Un termo tiene dobles paredes de vidrio, habiéndose vaciado de aire el espacio entre dichas paredes para evitar las pérdidas por conducción y convección. Para reducir las pérdidas por radiación, se cubren las paredes con una lámina de plata que es altamente reflectante y por tanto, mal emisor y mal absorbedor de radiación.

El cuerpo negro

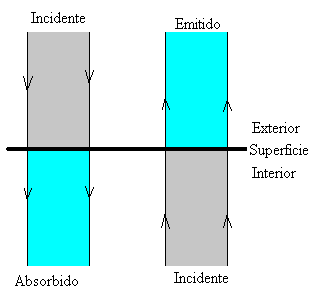
La superficie de un cuerpo negro es un caso límite, en el que toda la energía incidente desde el exterior es absorbida, y toda la energía incidente desde el interior es emitida.

No existe en la naturaleza un cuerpo negro, incluso el negro de humo refleja el 1% de la energía incidente.

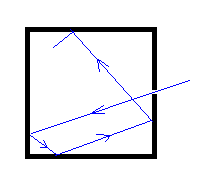
Sin embargo, un cuerpo negro se puede sustituir con gran aproximación por una cavidad con una pequeña abertura. La energía radiante incidente a través de la abertura, es absorbida por las paredes en múltiples reflexiones y solamente una mínima proporción escapa (se refleja) a través de la abertura. Podemos por tanto decir, que toda la energía incidente es absorbida.

La energía perdida por radiación es la diferencia entre la radiación emitida por el cuerpo y absorbida desde el ambiente que lo rodea que son a su vez, proporcionales a la cuarta potencia de sus temperaturas absolutas (Ley de Stefan)

${\displaystyle \frac{dQ}{dt}\propto \left(T^4-T_a^4\right)}$

T es la temperatura del cuerpo y T_a la temperatura ambiente.

No hay convección, solamente radiación

Comenzamos estudiando el efecto del intercambio de energía exclusivamente por radiación. Supongamos que el cuerpo está en un recipiente en el que se ha hecho el vacío, por lo que los intercambios de calor por conducción y convección son despreciables.

El cuerpo a una temperatura T emite energía por unidad de tiempo, eσST⁴. Donde σ=5.67·10^-8(Wm^-2K^-4) es la constante de Boltzmann, e es la emisividad de la superficie que supondremos constante y S es el área del cuerpo.
La emisividad e es el cociente entre la energía total emitida por un cuerpo en la unidad de tiempo a la temperatura T, y la energía que emitiría un cuerpo negro a la misma temperatura T. Es una propiedad de la superficie del cuerpo.

La energía absorbida por el cuerpo en la unidad de tiempo es, $e\sigma S{T}_a^4$

La variación de temperatura T del cuerpo que supondremos la misma tanto en el interior como en la superficie es.

${\displaystyle mc\frac{dT}{dt}=-e\sigma S{T}^4+e\sigma S{T}_a^4}$

m es la masa del cuerpo y c su calor específico

Haciendo los cambios de variable, llegamos a la ecuación

${\displaystyle \begin{array}{l}\tau =\frac{e\sigma S{T}_a^3}{mc}t\theta =\frac{T}{T_a}\\ -\frac{d\theta }{\left({\theta }^4-1\right)}=d\tau \end{array}}$

Que integramos entre θ₀ y θ que son las temperaturas reducidas en el instante τ=0 y en el instante τ.

Para calcular el integrando, descomponemos la fracción en suma de fracciones más simples.

${\displaystyle \begin{array}{l}{\displaystyle {\int }_{{\theta }_0}^{\theta }\frac{-1}{\left({\theta }^4-1\right)}}d\theta \\ \frac{-1}{x^4-1}=\frac{Ax+B}{x^2+1}+\frac{C}{x-1}+\frac{D}{x+1}\end{array}}$

A=0, B=1/2, C=-1/4, D=1/4.

O bien, utilizando la función MATLAB residue.

>> a=[-1];
>> b=[1 0 0 0 -1];
>> [c,r]=residue(a,b)
c =
   0.2500          
  -0.2500          
   0.0000 - 0.2500i
   0.0000 + 0.2500i
r =
  -1.0000          
   1.0000          
   0.0000 + 1.0000i
   0.0000 - 1.0000i

Fijarse que

${\displaystyle \frac{-0.25i}{x-i}+\frac{0.25i}{x+i}=\frac{0.5}{x^2+1}}$ ;

>> -0.25*i/(x-i)+0.25*i/(x+i)
ans =- i/(4*(x - i)) + i/(4*(x + i))
>> simplify(ans)
ans =1/(2*(x^2 + 1))

La integral de la función es la suma de integrales inmediatas

${\displaystyle \begin{array}{l}{\displaystyle \int \left(\frac{1}{2}\frac{1}{x^2+1}-\frac{1}{4}\frac{1}{x-1}+\frac{1}{4}\frac{1}{x+1}\right)}dx=\\ \frac{1}{2}\arctan (x)-\frac{1}{4}\log (x-1)+\frac{1}{4}\log (x+1)\end{array}}$

Finalmente, obtenemos la función implícita τ=f(θ)

${\displaystyle \tau =-\frac{1}{4}\ln \frac{\left|\theta -1\right|}{\left|{\theta }_0-1\right|}+\frac{1}{4}\ln \frac{\left|\theta +1\right|}{\left|{\theta }_0+1\right|}+\frac{1}{2}\left(\arctan \theta -\arctan {\theta }_0\right)}$

Con estos cambios de variable obtenemos una función que describe el proceso de enfriamiento exclusivamente por radiación, independientemente de las características del cuerpo, descrito por las variables (e, S, m, c) , la temperatura inicial T₀ del cuerpo y la ambiente T_a. Representamos la función θ(τ) para dos valores iniciales de la temperatura θ₀=1.8 y θ₀=0.2

ssyms x x0;
tau=-log((x-1)/(x0-1))/4+log((x+1)/(x0+1))/4+(atan(x)-atan(x0))/2;
hold on
y=subs(tau,x0,1.8);
ezplot(y,[0.999 1.8])
y=subs(tau,x0,0.2);
hg=ezplot(y,[0.2 0.999]);
set(hg,'color','r')
axis([0.2 1.8 0 1.6])

xlabel('\theta')
ylabel('\tau')
grid on
title('Enfriamiento por radiación')
hold off
view(-90,90)
set(gca, 'ydir', 'reverse');

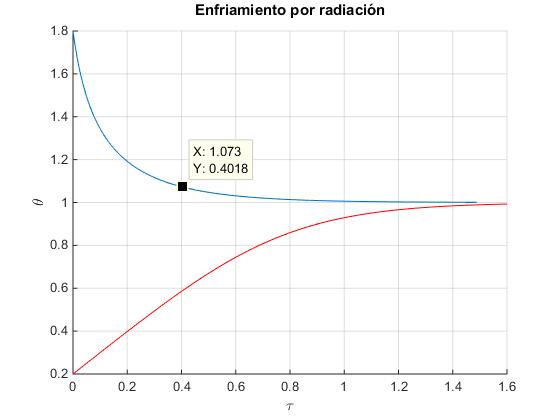
Fijamos el valor de theta_0 (θ₀) en 1.8 y le damos valores a theta (θ) entre 1.8 y 0.99, obteniendo los correspondientes valores de tau (τ) para representar la función τ=f(θ), (en color azul). Posteriormente, intercambiamos los ejes, mediante el comando view, de modo que el eje X es ahora τ y el eje Y es θ.

Trazamos una nueva gráfica (en color rojo) estableciendo el valor inicial de la temperatura reducida θ₀ en 0.2.

De este modo, comparamos dos casos, cuando la temperatura inicial es mayor que la ambiente (enfriamiento) T₀>T_a y cuando la temperatura inicial es inferior a la ambiente T₀<T_a (calentamiento).

Cálculo de la temperatura T en un instante t

Supongamos que conocemos la temperatura absoluta inicial T₀, la temperatura ambiente T_a y las características del cuerpo: superficie total S, emisividad e, masa m, calor específico c, la constante σ=5.67·10^-8(Wm^-2K^-4). Queremos calcular la temperatura T del cuerpo en el instante t.

Primero, calculamos la temperatura reducida inicial θ₀ y el tiempo reducido τ, mediante

${\displaystyle \tau =\frac{e\sigma S{T}_a^3}{mc}t{\theta }_0=\frac{T_0}{T_a}}$

Dado el valor de τ, resolvemos la ecuación trascendente f(θ)-τ=0, por algún procedimiento numérico o utilizando la función solve de Math Symbolic o la función fzero de MATLAB.

En este ejemplo, suponemos que θ₀=1.8 y queremos calcular la temperatura reducida θ en el instante τ=0.4. Como vemos en la gráfica anterior, situando el cursor en la curva de color azul en el punto de abscisa τ=0.4, obtenemos aproximadamente θ=1.073

>> x0=1.8;
>> tau=0.4;
>> f=@(x) -log((x-1)/(x0-1))/4+log((x+1)/(x0+1))/4
+(atan(x)-atan(x0))/2-tau;
>> fzero(f,1.1)
ans =    1.0736

Que como vemos, se corresponde con el valor señalado en la gráfica y obtenido con Data cursor. Una vez que conocemos θ=1.0736, calculamos la temperatura T=T_a· θ.

En el caso de utilizar la función fzero tenemos que proporcionar un valor inicial próximo a la raíz buscada, que podemos encontrar en la gráfica.

Repetimos el cálculo, estableciendo la temperatura inicial reducida θ₀=0.2 queremos calcular la temperatura reducida θ en el instante τ=0.4

>> x0=0.2;
>> tau=0.4;
>> f=@(x) -log((x-1)/(x0-1))/4+log((x+1)/(x0+1))/4
+(atan(x)-atan(x0))/2-tau;
>> fzero(f,0.5)
ans =    0.5853

Calentamiento de un cuerpo expuesto al Sol

Cuando el cuerpo se expone a la radiación procedente del Sol o de una lámpara, absorbe una energía por unidad de tiempo, eS'Φ. Donde Φ es el flujo en W/m² de energía que incide en una dirección z sobre el cuerpo y S' es el área de la superficie del cuerpo perpendicular a dicha dirección.

${\displaystyle \begin{array}{l}mc\frac{dT}{dt}=-e\sigma S{T}^4+e\sigma S{T}_a^4+eS\text{'}\Phi \\ \frac{dT}{dt}=-\frac{e\sigma S}{mc}\left(T^4-T_b^4\right)\\ T_b^4=T_a^4+\frac{S\text{'}\Phi }{\sigma S}\end{array}}$

Obtenemos la misma ecuación diferencial, pero con una temperatura T_b mayor que T_a. T_b es la temperatura constante que alcanza el cuerpo en el estado estacionario, es decir, cuando dT/dt=0. En ese momento, la energía absorbida por el cuerpo es igual a la emitida por el mismo.

Radiación y convección

Incluimos en este apartado, el intercambio de energía H del cuerpo con el aire a la temperatura ambiente T_a, por conducción y radiación. En este caso H es proporcional a la diferencia de temperaturas entre el cuerpo T y el ambiente T_a. H=hS(T-T_a)

${\displaystyle mc\frac{dT}{dt}=-hS\left(T-T_a\right)-e\sigma S\left(T^4-T_a^4\right)}$

Haciendo el cambio de variable

${\displaystyle \begin{array}{l}\theta =\frac{T}{T_a}p=\frac{h}{e\sigma T_a^3}\tau =\frac{e\sigma S}{mc}{T}_a^{3}t\\ d\tau =-\frac{d\theta }{{\theta }^4+p\theta -p-1}\end{array}}$

Que integramos entre θ₀ y θ que son las temperaturas reducidas en el instante t=0 y en el instante t. Esta integral es complicada por lo que nos ayudamos de MATLAB para resolverla.

Obtenemos de nuevo, una función general que describe el proceso de enfriamiento por radiación y convección, pero ahora esta función depende de un parámetro p.

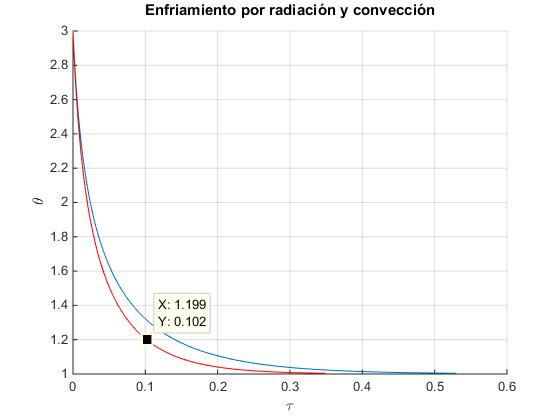
Vamos a representar la temperatura reducida θ en función del tiempo τ fijando la temperatura reducida inicial θ₀=3 y para dos valores del parámetro p=5.8 y p=11.6.

syms x;
y=int(-1/(x^4+5.8*x-6.8),x,3,x);
hold on
ezplot(y,[0.99 3])
y=int(-1/(x^4+11.6*x-12.6),x,3,x);
hg=ezplot(y,[3 0.99]);
set(hg,'color','r')
axis([1 3 0 0.6])
xlabel('\theta')
ylabel('\tau')
grid on
title('Enfriamiento por radiación y convección')
hold off
view(-90,90)
set(gca, 'ydir', 'reverse');

Cálculo de la temperatura T en un instante t

Supongamos que conocemos la temperatura absoluta inicial T₀, la temperatura ambiente T_a y las características del cuerpo: superficie total S, emisividad e, masa m, calor específico c, el coeficiente h para la transferencia del calor por convección, (o el cocciente h/e), la constante σ=5.67·10^-8(Wm^-2K^-4). Queremos calcular la temperatura T del cuerpo en el instante t.

Primero, calculamos la temperatura inicial reducida θ₀, el tiempo reducido τ y el parámetro p mediante las siguientes fórmulas

${\displaystyle {\theta }_0=\frac{T_0}{T_a}p=\frac{h}{e\sigma T_a^3}\tau =\frac{e\sigma S}{mc}{T}_a^{3}t}$

Resolvemos la ecuación trascendente f(θ)-τ=0, utilizando la función solve de MATLAB

${\displaystyle \tau ={\displaystyle {\int }_{{\theta }_0}^{\theta }\frac{-1}{{\theta }^4+p\theta -(p+1)}}d\theta }$

En la variable simbólica y guardamos el resultado de la integral para p=11.6 y para θ₀=3. Si queremos conocer el valor de la temperatura reducida θ en el instante τ=0.1, escribimos

>> syms x;
>> y=int(-1/(x^4+11.6*x-12.6),x,3,x);
>> solve(y-0.1)
ans =1.2056722642364635002270728688288

que es el valor que vemos en la gráfica y que hemos obtenido mediante Data cursor. Una vez que conocemos θ=1.206, calculamos la temperatura T=T_a· θ.

Dado que la expresión de la integral que guarda la variable simbólica y es muy larga para ser reproducida en estas páginas, no probamos la función fzero, como en el caso anterior.

Aproximación: ley del enfriamiento de Newton

Cuando realizamos la aproximación

${\displaystyle \begin{array}{l}\left(T^4-T_b^4\right)=\left(T^2+T_b^2\right)\left(T^2-T_b^2\right)=\left(T^2+T_b^2\right)\left(T+T_b\right)\left(T-T_b\right)\\ \approx 4T_b^3\left(T-T_b\right)\end{array}}$

Obtenemos la ley del enfriamiento de Newton

${\displaystyle \frac{dT}{dt}=-k\left(T-T_a\right)}$

Referencias

Ugo Besson. Cooling and warming laws: an exact analytical solution. Eur. J. Phys. 31 (2010) pp. 1107-1121