En esta página, vamos a analizar los cambios de temperatura del líquido contenido en un recipiente cuando por la resistencia del hornillo eléctrico circula una corriente alterna que hace que el líquido se caliente de forma periódica. Supondremos que el recipiente pierde calor y lo transfiere a la atmósfera y que estas pérdidas obedecen a la ley de enfriamiento de Newton. El régimen de temperaturas del líquido se puede dividir en dos partes:

• Un estado transitorio que dura un determinado tiempo (teóricamente infinito), pero que en la práctica viene determinado por la denominada constante de tiempo.

• A continuación, el estado estacionario caracterizado por una oscilación de temperaturas de amplitud constante, alrededor de un valor medio.

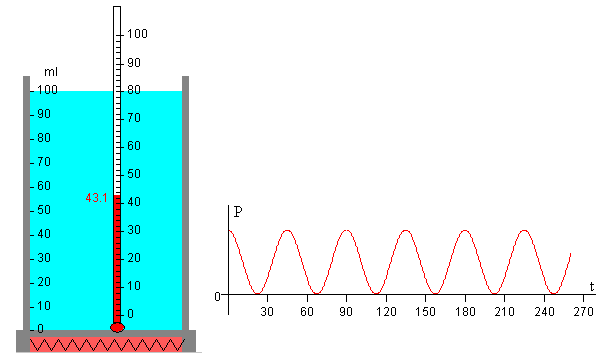
La potencia P suministrada por el hornillo eléctrico de resistencia R por el cual circula una corriente alterna de amplitud i₀ y de frecuencia angular ω es

${\displaystyle P=R{i}^2=R{i}_0^2{\cos }^2(\omega t)}$

El calor dQ=P·dt suministrado por el hornillo eléctrico en el intervalo de tiempo entre t y t+dt se invierte

• en elevar la temperatura del líquido mc·dT

• se transfiere a la atmósfera αS (T-T_a), de acuerdo con la ley del enfriamiento de Newton. Donde α es el coeficiente de intercambio de calor y S es el área del cuerpo en contacto con la atmósfera. T es la temperatura del líquido y T_a es la temperatura ambiente

${\displaystyle \begin{array}{l}P=\frac{dQ}{dt}=mc\frac{dT}{dt}+\alpha S(T-T_a)\\ \frac{dT}{dt}=\frac{R{i}_0^2{\cos }^2(\omega t)}{mc}-\frac{\alpha S}{mc}(T-T_a)\\ \frac{dT}{dt}+\frac{\alpha S}{mc}T=\frac{\alpha S}{mc}{T}_a+\frac{R{i}_0^2{\cos }^2(\omega t)}{mc}\\ \frac{dT}{dt}+\frac{\alpha S}{mc}T=\frac{\alpha S}{mc}{T}_a+\frac{R{i}_0^2}{2mc}+\frac{R{i}_0^2}{2mc}\cos (2\omega t)\end{array}}$

La solución de esta ecuación diferencial es la suma de la solución particular de la forma

T₁=A+B·cos(2ωt)+C·sin(2ωt)

y de la solución de la ecuación diferencial homogénea

Introducimos esta solución en la ecuación diferencial para determinar los coeficientes A, B y C.

${\displaystyle A=T_a+\frac{R{i}_0^2}{2\alpha S}B=\frac{R{i}_0^2}{4{\omega }^2{m}^2{c}^2+{\alpha }^2{S}^2}mc\omega C=\frac{R{i}_0^2}{4{\omega }^2{m}^2{c}^2+{\alpha }^2{S}^2}\frac{\alpha S}{2}}$

La solución particular se escribe

${\displaystyle T_1=T_a+\frac{R{i}_0^2}{2\alpha S}+\frac{R{i}_0^2}{4{\omega }^2{m}^2{c}^2+{\alpha }^2{S}^2}\left(mc\omega \text{ sin(2}\omega t\text{)}+\frac{\alpha S}{2}\text{cos(2}\omega t\text{)}\right)}$

La solución de la ecuación diferencial homogénea

${\displaystyle \frac{dT}{dt}+\frac{\alpha S}{mc}T=0T_2=D·\exp \left(-\frac{\alpha S}{mc}t\right)}$

La solución completa de la ecuación diferencial es

${\displaystyle \begin{array}{l}T=T_1+T_2=T_a+\frac{R{i}_0^2}{2\alpha S}+\\ \frac{R{i}_0^2}{4{\omega }^2{m}^2{c}^2+{\alpha }^2{S}^2}\left(mc\omega \sin \left(2\omega t\right)+\frac{\alpha S}{2}\cos \left(2\omega t\right)\right)+D\exp \left(-\frac{\alpha S}{mc}t\right)\end{array}}$

El coeficiente D se determina a partir de las condiciones iniciales. En el instante t=0, la temperatura del líquido contenido en el recipiente es la ambiente T_a.

${\displaystyle \begin{array}{l}T=T_a+\frac{R{i}_0^2}{2\alpha S}+\frac{R{i}_0^2}{2\sqrt{4{\omega }^2{m}^2{c}^2+{\alpha }^2{S}^2}}\text{cos(2}\omega t-\phi \text{)}+D\exp \left(-\frac{\alpha S}{mc}t\right)\\ D=-\frac{R{i}_0^2}{2\alpha S}-\frac{R{i}_0^2\alpha S}{2(4{\omega }^2{m}^2{c}^2+{\alpha }^2{S}^2)}\tan \phi =2\omega \frac{mc}{\alpha S}\end{array}}$

Definimos los parámetros

${\displaystyle \tau =\frac{mc}{\alpha S}K=\frac{R{i}_0^2}{mc}}$

El primero τ se denomina constante de tiempo. La temperatura T del líquido en función del tiempo t se expresa de forma más simple.

${\displaystyle \begin{array}{l}T=T_a+\frac{K\tau }{2}+\frac{K\tau }{2\sqrt{1+4{\omega }^2{\tau }^2}}\text{cos(2}\omega t-\phi \text{)}+D\exp (-t/\tau )\\ D=-\frac{K\tau }{2}-\frac{K\tau }{2(1+4{\omega }^2{\tau }^2)}\tan \phi =2\omega \tau \end{array}}$

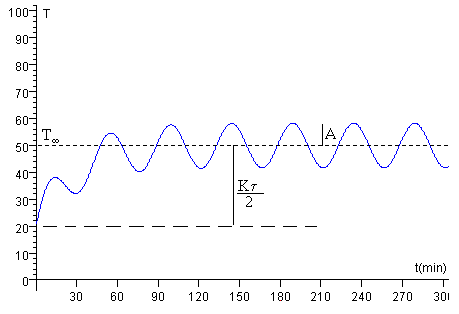
La temperatura T crece desde T_a debido al calentamiento del líquido del recipiente, sigue un comportamiento complejo durante un cierto tiempo, hasta que alcanza el estado estacionario (teóricamente cuando t→∞). Si la constante de tiempo τ es pequeña el estado estacionario se alcanza rápidamente. El último término (la exponencial decreciente) acaba tendiendo a cero y el estado estacionario se describe por una temperatura que oscila con frecuencia 2ω y amplitud A, alrededor del valor medio T_∞, tal como se aprecia en la figura.

${\displaystyle \begin{array}{l}T=T_{\infty }+\frac{K\tau }{2\sqrt{1+4{\omega }^2{\tau }^2}}\text{cos(2}\omega t-\phi \text{)}\\ T_{\infty }=T_a+\frac{K\tau }{2}\end{array}}$

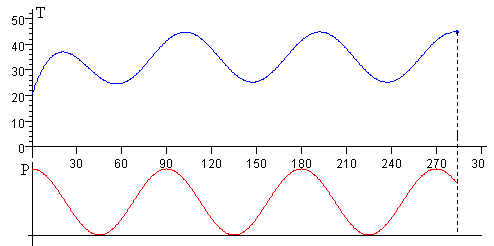
La temperatura T (en color azul) está desfasada φ respecto de la potencia P (en color rojo), tal como se aprecia en la figura (más abajo)

${\displaystyle P=R{i}_0^2{\cos }^2(\omega t)=\frac{R{i}_0^2}{2}+\frac{R{i}_0^2}{2}\cos (2\omega t)}$

Elaboramos un script en el que se establece:

• La masa de líquido en m=0.1 kg

• La potencia máxima suministrada por el hornillo $R{i}_0^2=12\text{W}$

• El calor específico c del líquido en J/(g ºC) actuando en la barra de desplazamiento titulada Calor específico. Por ejemplo, el calor específico del agua es 4180 J/(kg ºC)

• El periodo 2π/ω en minutos de la corriente alterna que circula por el hornillo.

• El coeficiente αS (de proporcionalidad en la ley del enfriamiento de Newton).

• La temperatura ambiente, T_a

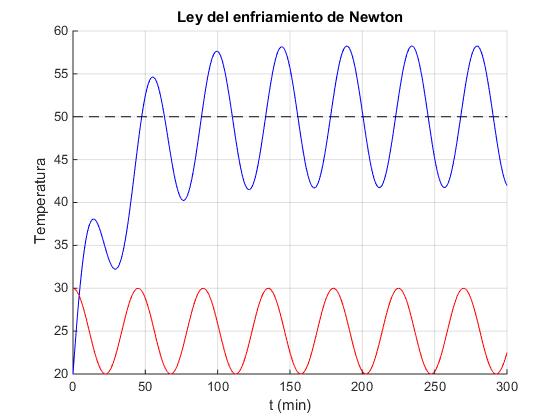
Se puede observar el desfase entre la gráfica de la temperatura (en color azul) y la gráfica de la potencia eléctrica suministrada (en color rojo), una vez que se ha establecido el estado estacionario.

Observamos el estado transitorio cuando la constante de tiempo τ es grande, es decir, cuando el coeficiente αS es pequeño y el calor específico c es grande.

La línea horizontal a trazos de color negro marca la T_∞, la temperatura media alrededor de la cual oscila la temperatura, cuando se ha establecido el estado estacionario.

m=0.1; %masa de líquido kg
W=12; %potencia en watios
c=3000; %calor específico J/(kg??C) 
P=90; %periodo en minutos de la corriente alterna
aS=0.2; %coeficiente de las pérdidas de calor
Ta=20; % temperatura ambiente

w=2*pi/(P*60); %frecuencia angular
k=W/(m*c); 
tau=(m*c)/aS;  %constante de tiempo
cte=k*tau/2+k*tau/(2*(1+4*w^2*tau^2));
fase=atan(2*w*tau);

t=0:300; %en minutos
T=Ta+k*tau/2+k*tau*cos(2*w*t*60-fase)/(2*sqrt(1.0+4*w^2*tau^2))
-cte*exp(-t*60/tau);
p=Ta+10*cos(w*t*60).^2; %potencia
hold on
plot(t,T,'b',t,p,'r')
Tfin=Ta+k*tau/2; %temperatura media final
line([0 t(end)],[Tfin Tfin],'linestyle','--','color','k');
title('ley del enfriamiento de Newton')
xlabel('t (min)')
ylabel('Temperatura')
grid on  
hold off

Obtenemos el mismo resultado mediante Math Symbolic. Partimos de la ecuación diferencial de primer orden que integramos mediante dsolve

${\displaystyle \begin{array}{l}\frac{dT}{dt}+\frac{\alpha S}{mc}T=\frac{\alpha S}{mc}{T}_a+\frac{R{i}_0^2}{2mc}+\frac{R{i}_0^2}{2mc}\cos \left(2\omega t\right)\\ \frac{dT}{dt}+aT=a{T}_a+b+b\cos \left(2\omega t\right)\\ a=\frac{\alpha S}{mc}=\frac{0.2}{0.1·3000}=\frac{1}{1500}\\ b=\frac{R{i}_0^2}{2mc}=\frac{12}{2·0.1·3000}=0.02\\ \omega =\frac{2\pi }{P}=\frac{2\pi }{90·60}=\frac{\pi }{2700}\end{array}}$

syms Ta a b w;
T=dsolve('DT+a*T=a*Ta+b+b*cos(2*w*t)','T(0)=Ta');
TT=subs(T,{Ta,a,b,w},{20,1/1500,0.02,pi/2700});
ezplot(TT,[0,300*60])  %300 minutos
title('Ley del enfriamiento de Newton')
xlabel('t (s)')
ylabel('Temperatura')
grid on 

La representación gráfica que obtenemos es la curva de color azul de la figura anterior

Actividades

Se ha fijado

• La masa de líquido en m=0.1 kg

• La potencia máxima suministrada por el hornillo $R{i}_0^2=12\text{W}$

Se introduce

• El calor específico c del líquido en J/(g ºC), en el control titulado Calor específico. Por ejemplo, el calor específico del agua es 4.18 J/(g ºC)

• El periodo 2π/ω en minutos de la corriente alterna que circula por el hornillo, en el control titulado Periodo

• El coeficiente αS (de proporcionalidad en la ley del enfriamiento de Newton), en el control titulado Pérdidas.

Se pulsa el botón titulado Nuevo

En la parte derecha, se representa en color azul:

• En el eje horizontal, el tiempo en minutos
• En el eje vertical, la temperatura T del líquido contenido en el recipiente.
• En color rojo, la potencia P proporcional a cos²(ωt) suministrada por el hornillo

Se puede observar el desfase entre las dos funciones del mismo periodo, una vez que se ha establecido el estado estacionario.

Observamos el estado transitorio cuando la constante de tiempo τ es grande, es decir, cuando el coeficiente αS es pequeño, y el calor específico c es grande.

Si el coeficiente αS es muy pequeño, la temperatura del líquido se incrementa. Cuando llega a 100 ºC la simulación se detiene, invitando al usuario a cambiar los valores de los parámetros.

Referencias

Krupska A., Krupski M., Konarski J. Phase dalay effect in a thermally homogeneous system heated periodically Eur. J. Phys. 22 (2001) pp. 133-138