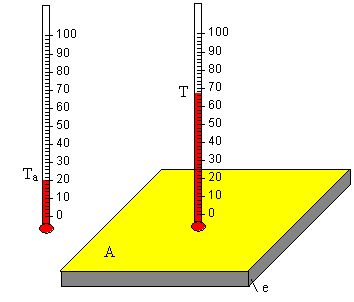
Consideremos una placa de área A y espesor e, que está a la temperatura ambiente T_a. La superficie de la placa de área A está pintada de negro. En un instante dado, se expone al Sol que ilumina la placa con una intensidad constante de I W/m². Vamos a determinar la evolución de la temperatura T de la placa a medida que transcurre el tiempo.

Supondremos que:

• La superficie de la placa pintada de negro absorbe toda la energía solar que recibe, en cada segundo I·A.
• Es aplicable la ley de enfriamiento de Newton, por lo que la placa pierde en cada segundo una energía αS(T-T_a). Donde T es la temperatura de la placa, S es el área de la placa en contacto con el ambiente y α es un parámetro a determinar experimentalmente.

La variación de la temperatura T de la placa con el tiempo se obtiene integrando la ecuación diferencial de primer orden

${\displaystyle mc\frac{dT}{dt}=-\alpha S(T-T_{\mathrm{a}})+I·A}$

donde m=ρAe es la masa de la placa y c es el calor específico y ρ la densidad del material que está hecha la placa.

${\displaystyle \frac{dT}{dt}+kT=k{T}_{\infty }k=\frac{\alpha S}{\rho Aec}{T}_{\infty }=T_{\mathrm{a}}+\frac{I}{\rho eck}}$

Integramos la ecuación diferencial de primer orden con la condición inicial siguiente: en el instante t=0, la temperatura de la placa es T_a.

${\displaystyle T=(T_{\mathrm{a}}-T_{\infty })\exp (-kt)+T_{\infty }}$

Al cabo de un tiempo muy grande t→∞ la placa alcanza la máxima temperatura T_∞.

Ejemplo:

• Intensidad de la radiación solar  I=700 W/m²

• Temperatura ambiente T_a=20ºC

• Espesor de la placa e=2 mm

• Material aluminio: ρ=2700 kg/m³ y c=880 J/(kgºC)

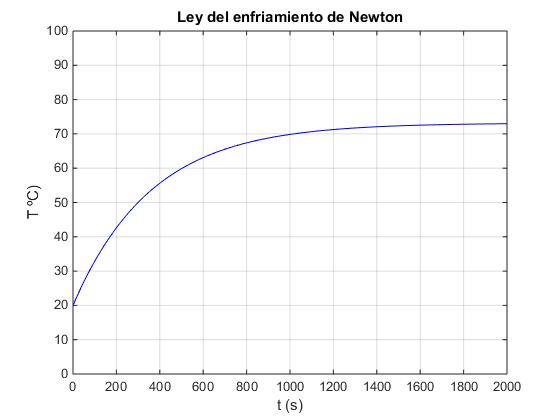
• La constante k=0.00277 s^-1

La máxima temperatura que alcanza la placa cuando se ilumina indefinidamente t→∞ es

${\displaystyle T_{\infty }=T_{\mathrm{a}}+\frac{I}{\rho eck}{T}_{\infty }=20+\frac{700}{2700·0.002·880·2.77·{10}^{-3}}=73.1º\text{C}}$

Ta=20; %temperatura inicial de la placa y ambiente
k=0.00277; %constante
I=700; %intensidad de la radiación incidente
e=0.002; %espesor de la placa
rho=2700; %densidad del aluminio
c=880; %calor específico del aluminio
Tf=Ta+I/(rho*e*c*k); %temperatura final

t=0:10:2000;
T=(Ta-Tf)*exp(-k*t)+Tf;
plot(t,T,'b')
ylim([0 100])
grid on
xlabel('t (s)')
ylabel('T (°C)')
title('Ley del enfriamiento de Newton')

Actividades

Se introduce

• La intensidad de la energía de la radiación solar que ilumina la placa en W/m² en el control titulado Intensidad sol

• El espesor de la placa e, en mm en el control de edición titulado Espesor

• La temperatura ambiente T₀ se ha fijado en 20ºC.

• El material de la placa es aluminio ρ=2700 kg/m³ y c=880 J/(kgºC)

Se pulsa el botón titulado Nuevo

La placa se calienta e incrementa su temperatura durante 20 minutos=1200 s hasta alcanzar la temperatura final T_f. Después se deja de iluminar la placa y esta se enfría.

En color rojo se dibuja la curva de calentamiento y en color azul la de enfriamiento.

La línea de puntos de color rojo es la asíntota horizontal T_∞ de la curva que describe el calentamiento de la placa.

Ejemplo:

• Intensidad de la radiación solar  I=700 W/m²
• Temperatura ambiente T₀=20ºC
• Espesor de la placa e=2 mm
• Material aluminio: ρ=2700 kg/m³ y c=880 J/(kgºC)

Se ilumina la placa, al cabo de 1200 s alcanza una temperatura de T_f=71.3 ºC

Se deja de iluminar la placa, se pone el contador de tiempo a cero, y al cabo de t=1000 s la temperatura ha bajado a 23.2 ºC

Conocida la temperatura inicial T_f =71.3º y la temperatura en el instante t=1000 s, T=23.2 durante el proceso de enfriamiento, calculamos la constante k.

T=T₀+(T_f-T₀)exp(-kt)

23.2=20+(71.3-20)exp(-k·1000)

${\displaystyle -k·1000=\ln \left(\frac{3.2}{51.3}\right)k=2.77·{10}^{-3}{\text{s}}^{-\text{1}}}$

La máxima temperatura que alcanza la placa cuando se ilumina indefinidamente t→∞ es

${\displaystyle T_{\infty }=T_0+\frac{I}{\rho eck}{T}_{\infty }=20+\frac{700}{2700·0.002·880·2.77·{10}^{-3}}=73.1º\text{C}}$

Referencias

Gil S., Mayochi M., Pelliza L. J., Experimental estimation of the luminosity of the Sun. Am. J. Phys. 74 (8) August 2006, pp. 728-733