El efecto invernadero.

Supongamos que el Sol es una esfera de radio R y medimos la intensidad de la radiación solar a una distancia r del centro del Sol, por ejemplo en la Tierra.

La energía emitida por el Sol, supuesto un cuerpo negro a la temperatura T es

P=4πR²σT⁴

Si suponemos que el Sol emite en todas las direcciones de forma isótropa. La intensidad de la radicación solar a una distancia r del centro del Sol es

$I = \frac{P}{4 π r^{2}} = σ T^{4} \frac{R^{2}}{r^{2}}$

Datos:

Constante de Stefan-Boltzmann, σ=5.67·10^-8(Wm^-2K^-4).
Radio del Sol, R=6.96·10⁸m
Distancia media entre la Tierra y el Sol, r=1.49·10¹¹ m.
Intensidad de la radiación solar medida en la órbita de la Tierra, I=1390 W/m²

Lo que nos da una temperatura T=5790 K o del orden de 6000 K.

Intensidad de la radiación solar medida en la órbita de la Tierra se denomina constante solar y el valor que aparece en muchos textos es de S=1367 W/m²

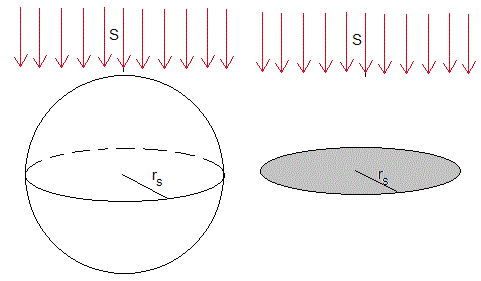
Una esfera de radio r_s (la Tierra) se encuentra a una distancia r del centro del Sol. Si r es muy grande, las ondas electromagnéticas procedentes del Sol serán aproximadamente planas, los rayos procedentes del Sol que llegan a media esfera serán paralelos tal como se muestra en la figura (más abajo).

En la página titulada Aplicaciones la ley de Stefan-Boltzmann. Equilibrio térmico, demostramos que la energía por unidad de tiempo recibida por la media esfera iluminada es igual a la energía recibida por una placa circular de radio r_s

$S π r_{s}^{2} = \frac{S}{4} 4 π r_{s}^{2}$

El modelo más simple

Una fracción a de la radiación incidente, denominada albedo, se refleja por la superficie de la Tierra. La energía neta que recibe la Tierra en la unidad de tiempo es

$(1 - a) π r_{s}^{2} S$

Supondremos que la Tierra es un cuerpo negro a la temperatura T que produce una radiación con intensidad σT⁴. La radiación total emitida por la Tierra es

$σ T^{4} (4 π r_{s}^{2})$

En el equilibrio

$\begin{array}{l} (1 - a) π r_{s}^{2} S = σ T^{4} (4 π r_{s}^{2}) \\ σ T^{4} = (1 - a) \frac{S}{4} \end{array}$

El albedo a=0.30. Sustituyendo valores obtenemos T=254.9 K que está 33 °C por debajo de la temperatura media 288 K de la superficie de la Tierra y esto es debido al efecto invernadero

Al final de la página web titulada El cuerpo negro, hay un programa interactivo que representa la intensidad por unidad de longitud de onda en el eje vertical y la longitud de onda en μm (10^-6 m) en el eje horizontal

La radiación incidente proviene del Sol, suponiendo que es un cuerpo negro a la temperatura de 5790 K

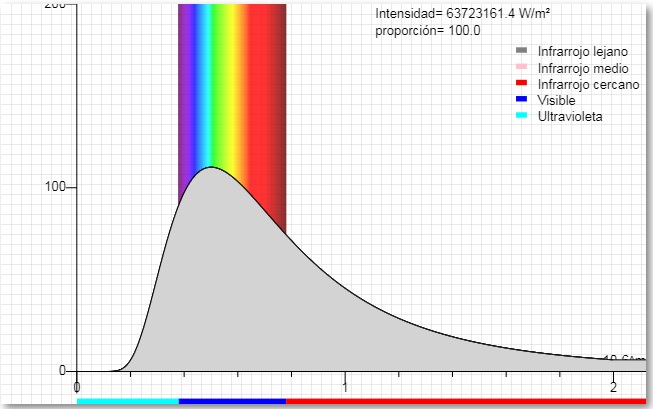
La mayor parte de la radiación se compone de infrarrojo cercano, visible y ultravioleta, de longitudes de onda cortas, medidas en décimas μm

La radiación proveniente de la Tierra, supuesto un cuerpo negro a la temperatura de 288 K

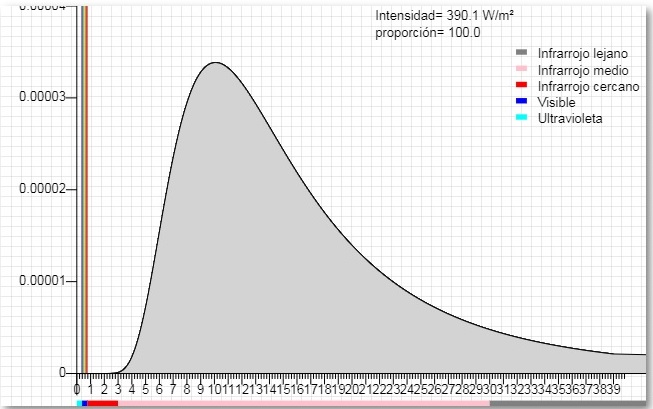
La mayor parte de la radiación se compone de infrarrojo medio y lejano, de longitudes de onda largas medidas en decenas y centenas de μm

En la tabla se recogen los datos de las distintas regiones del espectro, la longitud de onda se da en μm (10^-6 m).

Región del espectro	Intervalo (μm)
(1) Infrarrojo lejano	1000-30
(2) Infrarrojo medio	30-3
(3) Infrarrojo cercano	3-0.78
(4) Visible	0.78-0.38
(5) Ultravioleta	0.38-0006

Efecto invernadero

El efecto invernadero es el responsable de que la temperatura de la superficie de la Tierra sea más alta que la obtenida suponiendo que la Tierra se comporta como un cuerpo negro en equilibrio con la radiación proveniente del Sol.

El efecto invernadero se debe al hecho de que la atmósfera tiene un comportamiento diferente con respecto a la radiación de longitud de onda corta (entrante) y la radiación de longitud de onda larga (saliente). Mientras que la mayor parte de la radiación incidente, se compone de radiación visible, pasa a través de la atmósfera, la mayor parte de la radiación infrarroja emitida por la superficie de la Tierra es absorbida selectivamente por moléculas gaseosas.

Las moléculas de los gases que absorben radiación infrarroja son los causantes del efecto invernadero, entre ellos se encuentran vapor de agua, anhídrido de carbono CO₂, metano, óxido nitroso. Las concentraciones de metano y CO₂ se han incrementado exponencialmente en la era industrial debido a la intensa actividad humana.

Vamos a considerar un modelo simplificado formado por dos capas: la superficie de la Tierra y la atmósfera.

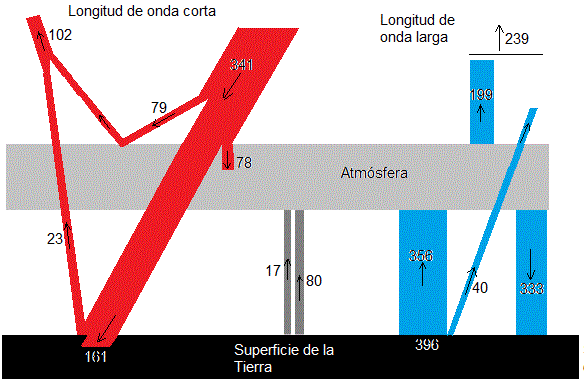
El balance de energía se agrupa en tres categorías:

La radiación incidente proveniente del Sol de longitudes de onda cortas, (en color rojo en la figura)
La radiación emitida por la superficie de la Tierra, de longitudes de onda largas, (en color azul en la figura)
La transferencia de calor entre la superficie de la Tierra y la atmósfera diferente a la radiación, (en color gris en la figura)

Radiación incidente. Radiación de longitud de onda corta

La energía solar promedio (por toda la Tierra y a lo largo del año) por unidad de superficie y tiempo (W/m²) proveniente del Sol, interceptada por la Tierra es S/4=341.7 W/m²
Una porción de la energía incidente se refleja al espacio por la atmósfera, las nubes y la superficie de la Tierra. La fracción de la radiación incidente que es reflejada se denomina albedo, alrededor del 102 W/m², un 30% de la radicación incidente
La atmósfera absorbe 23% de la radiación incidente (78 W/m²). La radiación utravioleta es absorbida por el ozono en la parte superior y media de la atmósfera. La radiación visible pasa a través del la atmósfera sin alteración
Una parte de la radiación incidente que llega a la superficie de la Tierra es absorbida (161 W/m²)

Sistema Tierra - atmósfera. Radiación de longitud de onda larga

El espectro de la radiación emitida por la superficie de la Tierra, corresponde a un cuerpo negro cuya temperatura es de 288 K (15 °C) (temperatura media global anual). La tierra emite $σ T_{s}^{4} = 396 {W/m}^{2}$
Debido a los gases y las nubes, la atmósfera absorbe el 90% de la radiación infrarroja y transmite un 10% al espacio exterior (40 W/m²). Esto ocasiona que la atmósfera se caliente e induce la emisión de radiación desde la atmósfera en todas las direcciones:

La atmósfera emite 199 W/m², hacia el espacio exterior ya que la parte superior de la atmósfera, se comporta como un cuerpo negro a la temperatura de 243 K, un valor entre las temperaturas más altas y más bajas medidas en la estratosfera

El flujo total de radiación infrarroja que escapa al espacio exterior (proveniente de la atmósfera y de la superficie de la Tierra) es de 239 W/m²

Se estima en 333 W/m² la radiación emitida por la parte inferior de la atmósfera y que llega a la superificie de la Tierra y corresponde a un cuerpo negro cuya temperatura es 276 K, que es la temperatura promedio de los primeros 5 km de la troposfera. Esta radiación es absorbida por la superficie de la Tierra

Transferencia de calor entre la superficie de la Tierra y la atmósfera

La evaporación y los cambios de fase (líquido-vapor) se estiman en 80 W/m²
La conducción del calor y convección se estiman en 17 W/m²

Balance energético

Atmósfera: 78+17+80+356-333-199=-1
Superficie de la Tierra: 161-17-80-396+333=1

La atmósfera y la superficie de la Tierra se encuentran en el estado estacionario

Modelo de dos capas

Consideremos dos capas de la misma área A:

La atmósfera de altura z_a, densidad ρ_a, calor específico c_a. Su temperatura uniforme es T_a
La superficie de la Tierra, de altura z_s, densidad ρ_s, calor específico c_s. Su temperatura uniforme es T_s

Denominamos S=1367/4=341.7 W/m² la constante solar efectiva

Radiación de longitud de onda corta

Se refleja una parte de la radiación incidente, a_aS

Se transmite una parte de la radiación incidente, t_aS

El resto de la radiación, (1-a_a-t_a)S se absorbe por la atmósfera

De la radiación que llega a la superficie de la Tierra t_aS, parte se refleja a_s(t_aS) y el resto se absorbe, (1-a_s)(t_aS). La parte reflejada en la superficie de la Tierra a_s(t_aS) llega a la atmósfera donde una parte es de nuevo reflejada, otra transmistida y el resto, absorbida. Por simplicidad, supondremos que la parte a_s(t_aS) es completamente absorbida por la atmósfera.

Radiación de longitud de onda larga

T_a es la temperatura de la atmósfera, emite hacia arriba (espacio exterior) y hacia abajo (superficie de la Tierra) radiación $e_{a} σ T_{a}^{4}$ , donde e_a es la emisividad de la atmósfera y T_a es su temperatura. La radiación que llega a la superficie de la Tierra es completamente absorbida

T_s es la temperatura de la superficie de la Tierra y emite radiación $e_{s} σ T_{s}^{4}$ , hacia la atmósfera. Donde e_s es la emisividad de la superficie

La radiación incidente en la atmósfera será reflejada $a_{a}^{'} e_{s} σ T_{s}^{4}$ , transmitida al espacio exterior, $t_{a}^{'} e_{s} σ T_{s}^{4}$ , y el resto absorbida, $(1 - a_{a}^{'} - t_{a}^{'}) e_{s} σ T_{s}^{4}$

La radiación reflejada hacia la superficie, $a_{a}^{'} e_{s} σ T_{s}^{4}$ es completamente absorbida

La transferencia de calor entre la superficie y la atmósfera

Se describe mediante k(T_s-T_a), donde k es la conductividad térmica y T_s-T_a la diferencia de temperaturas. Supondremos que es mayor la de la superficie de la Tierra

En la figura se recogen los flujos de radiación

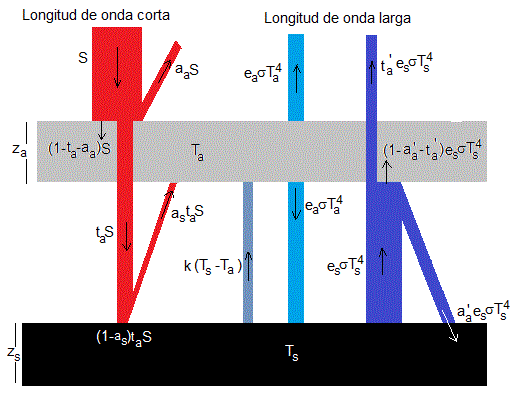
Balance energético

El flujo neto de energía por unidad de área y unidad de tiempo

Atmósfera

$\frac{δ Q_{a}}{A \cdot d t} = (1 - t_{a} - a_{a}) S + a_{s} t_{a} S - 2 e_{a} σ T_{a}^{4} + (1 - t_{a}^{'} - a_{a}^{'}) e_{s} σ T_{s}^{4} + k (T_{s} - T_{a})$

Superficie

$\frac{δ Q_{s}}{A \cdot d t} = (1 - a_{s}) t_{a} S - k (T_{s} - T_{a}) + e_{a} σ T_{a}^{4} - e_{s} σ T_{s}^{4} + a_{a}^{'} e_{s} σ T_{s}^{4}$

El calor emitido o absorbido modifica la temperatura de las capas

$\begin{array}{l} δ Q_{a} = m_{a} c_{a} d T_{a} = ρ_{a} A z_{a} c_{a} d T_{a} \\ δ Q_{s} = m_{s} c_{s} d T_{s} = ρ_{s} A z_{s} c_{s} d T_{s} \end{array}$

Llegamos al sistema de dos ecuaciones diferenciales

${\begin{cases} ρ_{a} z_{a} c_{a} \frac{d T_{a}}{d t} = (1 - t_{a} - a_{a}) S + a_{s} t_{a} S - 2 e_{a} σ T_{a}^{4} + (1 - t_{a}^{'} - a_{a}^{'}) e_{s} σ T_{s}^{4} + k (T_{s} - T_{a}) \\ ρ_{s} z_{s} c_{s} \frac{d T_{s}}{d t} = (1 - a_{s}) t_{a} S - k (T_{s} - T_{a}) + e_{a} σ T_{a}^{4} - (1 - a_{a}^{'}) e_{s} σ T_{s}^{4} \end{cases}$

Resolvemos el sistema de dos ecuaciones diferenciales por el procedimiento ode45 de MATLAB con las condiciones iniciales, en el instante t=0, las temperaturas de las capas son T_a0 y T_s0

Valores de los parámetros

S=341
σ=5.67·10^-8
a_a=0.30
t_a=0.52
a_s=0.11
a'_a=0.30
t'_a=0.06
e_s=0.90
e_a=0.90
k=2.7

Atmósfera

Calor especifico, c_a=200
Densidad, ρ_a=0.97
Espesor, z_a=3000

Superficie de la Tierra

Calor especifico, c_s=607
Densidad, ρ_s=4000
Espesor, z_s=400

En el sistema internacional de unidades S. I.

Las temperaturas iniciales se toman T_a=0, y T_s=0. El tiempo final se toma 90 años, 2.8382·10⁹ s.

S=1370/4; %constante solar efectiva
sigma=5.67e-8; %constante
a_a=0.30;
t_a=0.52;
a_s=0.11;
ap_a=0.30;
tp_a=0.06;
e_s=0.90;
e_a=0.90;
k=2.7; %conductividad térmica

rho_a=0.97; %densidad atmósfera
c_a=200; %calor específico
z_a=3000; %espesor capa
rho_s=4000; %densidad superficie
c_s=607; %calor específico
z_s=400; %espesor capa
tf=90*365*24*60*60; %tiempo final

f=@(Ta, Ts) ((1-a_a-t_a)*S+a_s*t_a*S+(1-ap_a-tp_a)*e_s*sigma*Ts^4-
2*e_a*sigma*Ta^4+k*(Ts-Ta))/(rho_a*c_a*z_a);
g=@(Ta, Ts) ((1-a_s)*t_a*S-(1-ap_a)*e_s*sigma*Ts^4+e_a*sigma*Ta^4-
k*(Ts-Ta))/(rho_s*c_s*z_s);
fg=@(t,x) [f(x(1), x(2)); g(x(1), x(2))];
[t,x]=ode45(fg,0:500000:tf,[0,0]);
plot(t,x)
grid on
xlabel('t')
legend('T_a', 'T_s', 'location', 'best')
ylabel('T_a, T_s');
title('Efecto invernadero')

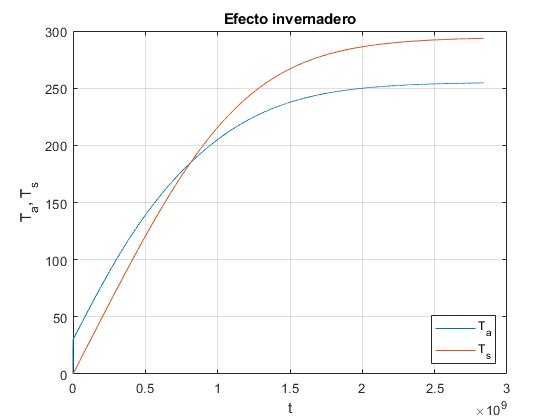
Las temperaturas en el instante t=90 años son próximas a T_a=254 K y T_s=293 K son próximas a las temperaturas en el estado estacionario. La temperatura de la superficie de la Tierra T_s no está muy lejos de la media 288 K. En cuanto a la temperatura de la atmósfera T_a, la de la parte superior (estratosfera) es 243 K y la de la parte inferior (troposfera) 276 K, el valor medio es 258 K cerca del valor calculado

>> x(end,1), x(end,2)
ans =  254.6160
ans =  293.5672

Estado estacionario

En el estado estacionario dT_a/dt=dT_b/dt=0. Resolvemos el sistema de dos ecuaciones con dos incógnitas para calcular T_a y T_s

${\begin{cases} (1 - t_{a} - a_{a}) S + a_{s} t_{a} S - 2 e_{a} σ T_{a}^{4} + (1 - t_{a}^{'} - a_{a}^{'}) e_{s} σ T_{s}^{4} + k (T_{s} - T_{a}) = 0 \\ (1 - a_{s}) t_{a} S - k (T_{s} - T_{a}) + e_{a} σ T_{a}^{4} - (1 - a_{a}^{'}) e_{s} σ T_{s}^{4} = 0 \end{cases}$

que no dependen de la composición y dimensiones de las capas, solamente de los parámetros

S=1370/4; %constante solar efectiva
sigma=5.67e-8; %constante
%parámetros
a_a=0.30;
t_a=0.52;
a_s=0.11;
ap_a=0.30;
tp_a=0.06;
e_s=0.90;
e_a=0.90;
k=2.7; %conductividad térmica

f=@(Ta, Ts) ((1-a_a-t_a)*S+a_s*t_a*S+(1-ap_a-tp_a)*e_s*sigma*Ts^4-
2*e_a*sigma*Ta^4+k*(Ts-Ta));
g=@(Ta, Ts) ((1-a_s)*t_a*S-(1-ap_a)*e_s*sigma*Ts^4+e_a*sigma*
Ta^4-k*(Ts-Ta));
fg=@(x) [f(x(1), x(2)), g(x(1), x(2))];

x0 =[300, 200]; %valor inicial
[x,fval] = fsolve(fg,x0); 
fprintf('La solución es Ta=%1.3f, Ts=%1.3f\n',x(1),x(2));
fprintf('Valores de la función = %g\n',fval)

Las temperaturas en el estado estacionario son: T_a=255.3 K y T_s=294.6 K

La solución es Ta=255.272, Ts=294.592
Valores de la función = 1.84741e-13
Valores de la función = -1.56319e-13

El lector puede cambiar el valor de uno de los parámetros, en particular a_a y a'_a, cada vez y ver su efecto sobre las temperaturas de la atmósfera T_a y de la superficie de la Tierra T_s en el estado estacionario

Referencias

Rhett Herman. Spreadsheet physics: Examples in meteorology and planetary science. Am. J. Phys. 77 (12) December 2009, pp. 1124-1129

P. Onorato, P Mascheretti, D DeAmbrosis. 'Home made' model to study the greenhouse effect and global warming. Eur. J. Phys. 32 (2011) pp. 363-376