Temperatura de un satélite

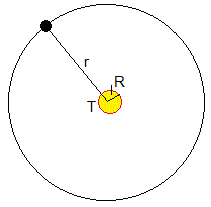
Una esfera de radio r_s se encuentra a una distancia r del centro del Sol. Si r es muy grande, las ondas electromagnéticas procedentes del Sol serán aproximadamente planas, los rayos procedentes del Sol que llegan a media esfera serán paralelos tal como se muestra en la figura (más abajo).

Denominamos $\overrightarrow{I}$ al vector que nos da la intensidad o energía emitida por el Sol en todas las frecuencias por unidad de tiempo y unidad de área. Lo pondremos, arbitrariamente, paralelo al eje Z, en el Sistema de Referencia situado en el centro de la esfera de radio r_s

${\displaystyle \overrightarrow{I}=-I\widehat{k}=-\sigma T^4\frac{4\pi R^2}{4\pi r^2}\widehat{k}\frac{W}{m^2}}$

T es la temperatura del Sol y R su radio, r es la distancia del centro del Sol a la órbita de la Tierra, supuesta circular

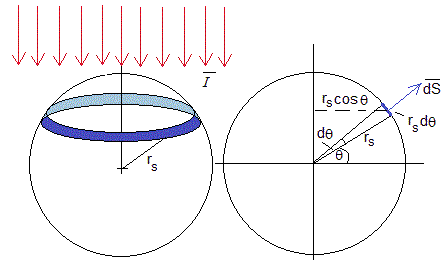
El flujo de energía (energía por unidad de tiempo) que se recibe en la porción dS de la superficie de la esfera es el producto escalar $\overrightarrow{I}·\overrightarrow{dS}$ .

La dirección del vector superficie $\overrightarrow{dS}$ es radial. El área dS es el producto de la longitud de la circunferencia 2πr_scosθ por la longitud del arco r_s·dθ, es decir, dS=2πr_s²cosθ·dθ

El flujo de energía que llega a la mitad iluminada de la esfera es

${\displaystyle \begin{array}{l}{{\displaystyle \int }}^{\text{}}\overrightarrow{I}·\overrightarrow{dS}={\displaystyle \int -IdS}\sin \theta =-2\pi I{r}_s^2{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\cos \theta \sin \theta ·d\theta =}-\pi I{r}_s^2{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\sin 2\theta ·d\theta =}\\ -I\left(\pi r_s^2\right)=-\sigma T^4\frac{R^2}{r^2}\pi r_s^2\end{array}}$

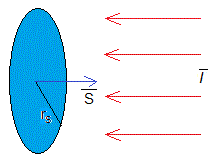
Que es lo mismo que una radiación uniforme de intensidad I W/m² incidiese perpendicularmente a una superficie plana de área πr_s²

En este problema se pretende calcular la temperatura de un satélite artificial cuya forma es la de una esfera de radio r_s=1 m. Supondremos que la temperatura del satélite es uniforme en toda su superficie y que está en una órbita cercana a la Tierra pero no en su sombra. Datos:

• Constante de Stefan-Boltzmann, σ=5.67·10^-8 (Wm^-2K^-4).
• Radio del Sol, R=6.96·10⁸ m
• Distancia entre la Tierra y el Sol, r=1.49·10¹¹ m.
• Temperatura del Sol, T=6000 K

1. El satélite absorbe en la unidad de tiempo energía procedente del Sol en todas las frecuencias

${\displaystyle \sigma T^4\frac{R^2}{r^2}\pi r_s^2}$

Supondremos que el satélite es un cuerpo negro a la temperatura T_s que emite energía por unidad de tiempo al espacio en todas las frecuencias

${\displaystyle 4\pi r_s^2\sigma T_s^4}$

En el equilibrio, igualando la emisión y absorción de energía, obtenemos

${\displaystyle T^4\frac{R^2}{r^2}=4T_s^4{6000}^4\frac{{(6.96·{10}^8)}^2}{{(1.49·{10}^{11})}^2}=4T_s^4}$

T_s=290 K=17ºC

>> r=1.49e11; %radio de la órbita circular de la Tierra
>> R=6.96e8; %radio del Sol
>> T=6000; %temperatura del Sol
>> Ts=nthroot(T^4*R^2/(4*r^2),4)
Ts =  289.9664

2. En muchas aplicaciones es necesario mantener el satélite tan frío como sea posible. Para enfriar el satélite se utiliza un recubrimiento que refleja la luz por encima de una frecuencia f_c tal que hf_c/k=1200 K

La intensidad de la radiación absorbida en el intervalo de frecuencias (0, f_c) es

$$\begin{gathered} {\displaystyle \begin{array}{l}W\left(\mathrm{0,}{f}_c\right)=\frac{2\pi k^4{T}^4}{c^2{h}^3}{\displaystyle \underset{0}{\overset{x_c}{\int }}\frac{x^3}{e^x-1}dx}x=\frac{hf}{kT}{x}_c=\frac{h{f}_c}{kT}=\frac{1200}{6000}=0.2\\ W\left(\mathrm{0,}{f}_c\right)=\frac{2\pi k^4{T}^4}{c^2{h}^3}\left({\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{x^3}{e^x-1}dx}-{\displaystyle \underset{x_c}{\overset{\infty }{\int }}\frac{x^3}{e^x-1}dx}\right)= \\ \frac{2\pi k^4{T}^4}{c^2{h}^3}\left(\frac{{\pi }^4}{15}-\frac{{\pi }^4}{15}F(x_c)\right)=\sigma T^4\left(1-F(x_c)\right)\end{array}} \end{gathered}$$

Donde la función F(x_c) se define

${\displaystyle F\left(x_c\right)=\frac{15}{{\pi }^4}{\displaystyle \underset{x_c}{\overset{\infty }{\int }}\frac{x^3}{e^x-1}}dx}$

>> format long
>> f=@(x) (x.^3)./(exp(x)-1);
>> integral(f,0.2,inf)*15/pi^4
ans =   0.999619337768793

La función F(x) se puede obtener mediante el desarrollo en serie

${\displaystyle F\left(x\right)=\frac{15}{{\pi }^4}{\displaystyle \sum _{n=1}^{\infty }\frac{\exp (-nx)}{n}}\left(x^3+\frac{3x^2}{n}+\frac{6x}{n^2}+\frac{6}{n^3}\right)}$

Tomando N=100 términos del desarrollo en serie

>> x=0.2;
>> n=1:100;
>> sum((exp(-n*x).*(x^3+(3*x^2)./n+(6*x)./n.^2+6./n.^3))./n)*15/pi^4
ans =   0.999619337768666

Lo que indica que la energía absorbida es solamente la pequeña proporción δ=1- F(0.2)=3.8066·10^-4 de la energía total incidente σT⁴ en todas las frecuencias.

La energía por unidad de tiempo absorbida por el satélite con el recubrimiento es, por tanto,

${\displaystyle \delta ·\sigma T^4\frac{R^2}{r^2}\pi r_s^2}$

Debido al recubrimiento son reflejadas hacia el interior del cuerpo cuya temperatura es T_s las radiaciones de frecuencia comprendida entre 0 a f_c

${\displaystyle \sigma T_s^4\left(1-F(x{\text{'}}_c)\right)x{\text{'}}_c=\frac{h{f}_c}{k{T}_s}=\frac{1200}{T_s}}$

La energía emitida por el cuerpo en la unidad de tiempo será

${\displaystyle 4\pi r_s^2\sigma T_s^{4}F(x{\text{'}}_c)}$

En el equilibrio, igualamos absorción y emisión

${\displaystyle \delta ·T^4\frac{R^2}{r^2}=4T_s^{4}F\left(\frac{1200}{T_s}\right)}$

Resolvemos la ecuación transcendente para calcular la temperatura T_s del satélite.

T_s=123 K

r=1.49e11; %radio de la órbita circular de la Tierra
R=6.96e8; %radio del Sol
T=6000; %temperatura del Sol
xc=0.2; %límite inferior de la integral
f=@(x) (x.^3)./(exp(x)-1);
delta=1-integral(f,xc,inf)*15/pi^4;
g=@(x) 4*x^4*integral(f,1200/x,inf)*15/pi^4-delta*T^4*R^2/r^2;
Ts=fzero(g,100)

Ts =  123.3346

3. Supongamos que el satélite artificial dispone de paneles solares que generan electricidad, la energía generada por los circuitos dentro del satélite actúa como una fuente de calor. Suponiendo que la potencia disipada es de 1000 W, calcular la temperatura final del satélite

La energía absorbida  más la generada internamente será igual a la energía disipada

$$\begin{gathered} {\displaystyle \begin{array}{l}\delta ·\sigma T^4\frac{R^2}{r^2}\pi r_s^2+1000=4\pi r_s^2\sigma T_s^{4}F(x{\text{'}}_c)x{\text{'}}_c=\frac{h{f}_c}{k{T}_s}=\frac{1200}{T_s}\\ 3.8066·{10}^{-4}·5.67·{10}^{-8}·{6000}^4\frac{{(6.96·{10}^8)}^2}{{(1.49·{10}^{11})}^2}\pi ·{1.0}^2+1000= \\ 4\pi ·{1.0}^2·5.67·{10}^{-8}{T}_s^{4}F\left(\frac{1200}{T_s}\right)\\ 0.61+1000=4\pi ·{1.0}^2·5.67·{10}^{-8}{T}_s^{4}F\left(\frac{1200}{T_s}\right)\end{array}} \end{gathered}$$

La energía generada internamente es muy superior a la energía absorbida procedente del Sol. Resolviendo la ecuación transcendente obtenemos

T_s=261 K

r=1.49e11; %radio de la órbita circular de la Tierra
R=6.96e8; %radio del Sol
T=6000; %temperatura del Sol
rs=1; %radio del satélite
sigma=5.67e-8; %constante
xc=0.2; %límite de frecuencias
f=@(x) (x.^3)./(exp(x)-1);
delta=1-integral(f,xc,inf)*15/pi^4;
g=@(x) 4*pi*rs^2*sigma*x^4*integral(f,1200/x,inf)*15/pi^4-1000-
delta*sigma*T^4*R^2*pi*rs^2/r^2;
Ts=fzero(g,200)

Ts =  261.0917

Variación de la temperatura de un pequeño cuerpo situado en el interior de una cavidad

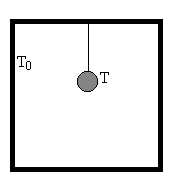
Supongamos un pequeño cuerpo esférico de radio r, suspendido en el interior de una gran cavidad en la que se ha hecho el vacío y cuyas paredes se encuentran a la temperatura T₀. Si la temperatura inicial de la bola esférica es T al cabo de un cierto tiempo, se habrá alcanzado el equilibrio en el que la temperatura de la esfera será la misma que la de las paredes de la cavidad.

Como hemos visto al estudiar las propiedades de la superficie de un cuerpo, el valor del coeficiente de absorción a está comprendido entre 0 (para un reflector perfecto) y 1 (para una superficie idealmente negra). En vez de a, se suele emplear la denominada emitancia relativa e de la superficie que es numéricamente igual a a.

1. Energía radiante emitida por el pequeño cuerpo

La cantidad de energía radiante emitida por unidad de área y por unidad de tiempo desde la superficie de un cuerpo a temperatura T, viene dada por la expresión

${\displaystyle I=e\sigma T^4{\text{W/m}}^{\text{2}}}$

La ley de Stefan-Boltzmann es también válida para cualquier otro cuerpo (gris) cuya superficie tenga un coeficiente de absorción (o emitancia) independiente de la longitud de onda.

Multiplicando por el área de la superficie del pequeño cuerpo, obtenemos la energía P_e que pierde el cuerpo en la unidad de tiempo debido a la emisión de la radiación.

${\displaystyle P_e=e\sigma T^{4}4\pi r^2}$

2. Energía radiante absorbida por el cuerpo

También incide energía radiante sobre la superficie del cuerpo. Una parte de la energía incidente es absorbida P_a que se obtiene multiplicando la intensidad de la radiación por el área de su superficie, por la fracción a de la energía incidente que es absorbida. Como hemos dicho, este factor a es numéricamente igual a e.

${\displaystyle P_a=e\sigma T_0^{4}4\pi r^2}$

3. Variación en la temperatura del cuerpo con el tiempo

La cantidad de energía neta por unidad de tiempo (perdida o ganada) es igual a la diferencia entre la energía radiante absorbida y la emitida .

${\displaystyle \frac{dQ}{dt}=P_a-P_e}$

La cantidad de energía radiante ganada (perdida) se emplea en aumentar (disminuir) la temperatura del cuerpo. Si la masa del cuerpo es m, y su calor específico del cuerpo es c_v, escribimos

${\displaystyle dQ=m{c}_{v}dT}$

La temperatura del cuerpo varía con el tiempo hasta que se establece el equilibrio térmico a la temperatura T₀ de las paredes de la cavidad.

${\displaystyle \frac{dT}{dt}=\frac{3e\sigma }{\rho c_{v}r}\left(T_0^4-T^4\right)}$

donde hemos sustituido la masa m por el producto de la densidad ρ por el volumen de la pequeña esfera de radio r.

Sabiendo que T_e es la temperatura de la esfera en el instante t=0, se integra esta ecuación diferencial.

${\displaystyle \begin{array}{l}{\displaystyle \underset{T_e}{\overset{T}{\int }}\frac{dT}{T_0^4-T^4}}=\frac{3e\sigma }{\rho c_{v}r}{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ {\displaystyle \underset{x_0}{\overset{x}{\int }}\frac{dx}{1-x^4}}=T_0^3\frac{3e\sigma }{\rho c_{v}r}t,x=\frac{T}{T_0}\\ \frac{1}{1-x^4}=\frac{Ax+B}{1+x^2}+\frac{C}{1-x}+\frac{D}{1+x}\{\begin{array}{l}A=\mathrm{0,}C=\frac{1}{4}\\ B=\frac{1}{2},D=\frac{1}{4}\end{array}\\ {\displaystyle \int \frac{dx}{1-x^4}}=\frac{1}{2}\arctan (x)+\frac{1}{4}\ln \frac{1+x}{1-x}\end{array}}$

El resultado de la integral definida es

${\displaystyle \frac{1}{2}\arctan \left(\frac{T}{T_0}\right)+\frac{1}{4}\ln \frac{T_0+T}{T_0-T}-\left\{\frac{1}{2}\arctan \left(\frac{T_e}{T_0}\right)+\frac{1}{4}\ln \frac{T_0+T_e}{T_0-T_e}\right\}=T_0^3\frac{3e\sigma }{\rho c_{v}r}t}$

Dado el tiempo t, resolvemos la ecuación transcendente en x=T/T₀ mediante la función fzero de MATLAB

El script, nos permite investigar los factores de los que depende el tiempo que tarda una bolita de radio r, densidad ρ, calor específico c_v, y emisividad e, en alcanzar el equilibrio térmico con una cavidad grande cuyas paredes se mantienen una temperatura constante T₀.

Investigaremos con cuatro materiales cuyas propiedades se proporcionan en la siguiente tabla

Se representa la temperatura del cuerpo en función del tiempo. En el eje vertical se mide la temperatura en grados centígrados, y en el eje horizontal se mide el tiempo en minutos.

sigma=5.67e-8; %constante de Stefan-Boltzmann
e=0.8; %emitancia menor que la unidad
T0=1200+273; %temperatura de la cavidad
Te=25+273;  %temperatura inicial de la esfera
rho=7880; %densidad del hierro
c=450; %calor específico del hierro
r=0.1; %radio de la bolita
k=3*e*sigma*T0^3/(rho*c*r);
cte=atan(Te/T0)/2+log((T0+Te)/(T0-Te))/4;

tt=linspace(0.1,20*60,100);
T=zeros(1,length(tt));
i=1;
for t=tt
    f=@(x) atan(x)/2+log((1+x)/(1-x))/4-cte-k*t;
    T(i)=fzero(f,[Te/T0,0.999])*T0-273; %grados C
    i=i+1;
end
plot(tt/60,T)
xlabel('t (min)')
ylabel('T ºC')
grid on
title('Temperatura de la bolita')

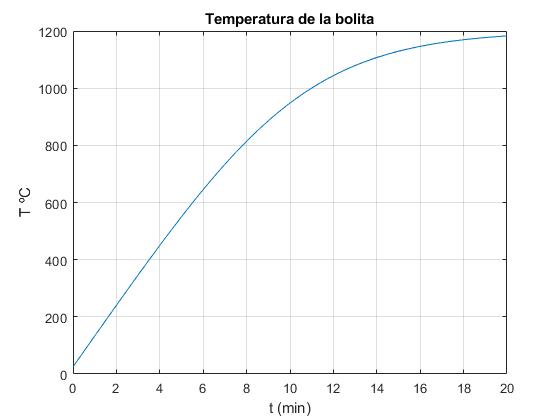
La intensidad de la radiación emitida por la esfera es proporcional a la cuarta potencia de su temperatura absoluta (cambia con dicha temperatura). La intensidad de la radiación absorbida por el pequeño cuerpo , es proporcional a la cuarta potencia de la temperatura absoluta de la cavidad (no se modifica).

El cuerpo aumenta su temperatura cuando la cantidad de energía absorbida en la unidad de tiempo es superior a la emitida, y disminuye su temperatura cuando la cantidad de energía emitida en la unidad de tiempo es superior a la absorbida. Cuando se alcanza la situación de equilibrio, ambas cantidades son iguales.

Referencias

Problema 3, propuesto en la XXIII Olimpiada Internacional de Física, Helsinki-Espoo, Finlandia (1992)