Efecto de la radiación sobre el movimiento de los cuerpos
Modelo mecánico
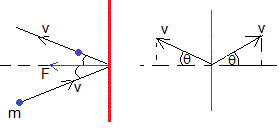
Una partícula de masa m y velocidad v choca elásticamente con una pared fija. El ángulo de incidencia θ que forma la dirección de la velocidad con la perpendicular a la pared es igual al ángulo con el que rebota
El cambio de momento lineal es 2mvcosθ. Para que la partícula cambie su momento lineal, la pared ejerce una fuerza F a lo largo de la dirección normal, igual y de sentido contrario a la que ejerce la partícula sobre la pared
Supongamos que un flujo de particulas n por unidad de volumen se mueven en un tubo de sección Sn con la misma velocidad v y chocan elásticamente con una placa de área S inclinada un ángulo θ tal como se muestra en la figura
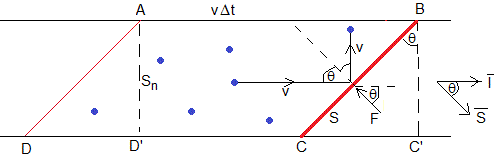
En el tiempo Δt chocan con la placa, las partículas contenidas en el volumen ABCD, que es igual al volumen ABC'D', es decir n·SnvΔt=n·SvΔt·cosθ
En cada choque, la partícula cambia el momento lineal, 2mvcosθ en la dirección perpendicular a la placa. El cambio de momento lineal en el intervalo de tiempo Δt debido al choque de todas las partículas es
(2mvcosθ)n·SvΔt·cosθ=2n·mv2cos2θ·SΔt
La fuerza que ejerce la placa para que las partículas cambien el momento lineal es
Su dirección es perpendicular a la placa. Las partículas ejercen una fuerza F sobre la placa de sentido contrario y una presión
Vela solar
Supongamos que un haz de luz monocromática de frecuencia f, de intensidad I (W/m2) ilumina la placa perfectamente reflectora, inclinada θ y de área S
En el tiempo Δt, la energía electromagnética en el volumen ABC'D' es ISnΔt y el número de fotones que chocan contra la placa en dicho intervalo de tiempo es ISnΔt/hf. Siendo hf la energía de cada fotón
En cada uno de los choques, la variación de momento lineal del fotón es 2(hf/c)cosθ. Siendo hf/c el momento lineal de un fotón
La fuerza que ejerce la placa reflectora para que las fotones cambien el momento lineal es
Independiente de la frecuencia f. La fuerza que ejercen los fotones de todas las frecuencias sobre la placa es igual y de sentido contrario. La presión de la radiación es el cociente F/S
Una vela solar es una superficie muy grande S hecha de un material de densidad muy pequeña cuya normal forma un ángulo θ con la dirección radial, que une el Sol con la vela. La masa de vela solar y la carga que puede transportar de instrumentación es pequeña
La intensidad de la radiación solar en la órbita de la Tierra supuesta circular de radio 1 UA=1.496·1011 m, denominada constante solar, es Is=1367 W/m2. Para una vela solar situada a esa distancia del Sol perpendicular a la dirección radial, θ=0, la presión de la radiación es 9.1·10-6 N/m2
Para una vela solar situada a una distancia r del Sol, la intensidad de la radiación solar (disminuye con la inversa del cuadrado de la distancia)
La vela está está sometida a dos fuerzas
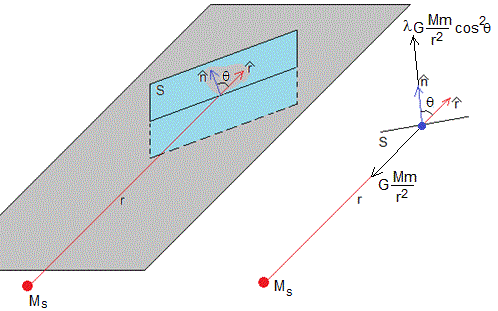
La fuerza repulsiva que ejerce la presión de la radiación sobre la superficie de la vela
La fuerza atractiva que ejerce el Sol sobre la vela
Se denomina λ (lightness number) al cociente
En términos de este parámetro, las fuerzas por unidad de masa sobre la vela solar se expresan,
Sea una vela solar de masa m=100 kg, cuadrada de 40 m de lado. La masa del Sol es Ms=1.98·1030 kg, la velocidad de la luz es c=3·108 m/s, la constante G=6.67·10-11 Nm2/kg2, la luminosidad del Sol es Ls=3.8445·1026 W
Obtenemos un número pequeño λ=0.0247. Cuyo significado es el cociente entre dos aceleraciones: la aceleración local de la gravedad g y la aceleración debida a la presión de la radiación an, cuando la vela es perpendicular a la dirección radial, θ=0
Para que λ=1, la densidad de la vela debería ser σ=m/S=0.0015 kg/m2, mucho menor que la densidad del papel de aluminio con el que se envuelven los alimentos: espesor 0.13 mm, densidad del aluminio 2700 kg/m3, el producto σ=0.351 kg/m2
Un satélite artificial perfectamente reflectante y de forma esférica
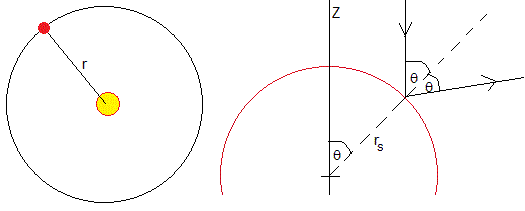
Una esfera de radio rs se encuentra a una distancia r del centro del Sol. Si r es muy grande, las ondas electromagnéticas procedentes del Sol serán aproximadamente planas, los rayos procedentes del Sol que llegan a media esfera serán paralelos tal como se muestra en la figura (más abajo).
Un fotón choca con la superficie esférica de radio rs perfectamente reflectora. La variación de momento lineal es
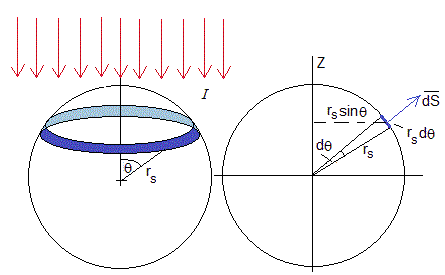
Sea If la energía por unidad de área y tiempo de la radiación monocromática de frecuencia f que llega al satélite procedente del Sol
El número de fotones de frecuencia f que inciden sobre la porción de superficie esférica comprendida entre θ y θ+dθ en el tiempo Δt es IfΔt·dS·cosθ/hf
La variación de momento lineal en dicho intervalo de tiempo es
La fuerza que ejerce la radiación monocromática de frecuencia f sobre la esfera es
La fuerza que ejerce la radiación de intensidad Is emitida por el Sol en todas las frecuencias en la posición del satélite artificial es
Ejemplo 1
Calculamos la fuerza que ejerce la radiación proveniente del Sol sobre un satélite artificial de radio rs=1 m, densidad ρ=2500 kg/m3, situado en la órbita de la Tierra alrededor del Sol, r=1.496·1011 m. La intensidad de la radiación, denominada constante solar, es Is=1367 W/m2. Comparamos esta fuerza con la fuerza de atracción que ejerce el Sol sobre el satélite artificial
Ejemplo 2
Consideremos dos esferas iguales de masa m, de radio rs situadas en el espacio exterior, en el interior de una caja cuyas paredes está a T=0 K (no emiten radiación).
Sus centros distan d>>rs. Supondremos que las esferas se comportan como cuerpos negros ideales a la temperatura T.
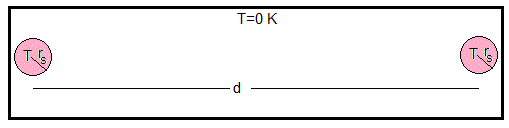
La fuerza de atracción entre las esferas es
La primera esfera ejerce una fuerza sobre la segunda debido a la radiación que emite. La condición d>>r asegura que la radiación que llega a la segunda esfera, se propaga en una dirección casi paralela a la recta que une los centros de ambas esferas
Donde Is es la intensidad de la radiación emitida por la primera esfera en la posición de la segunda, a una distancia d>>rs
La fuerza neta sobre cada esfera es la suma de una fuerza de atracción gravitatoria y una fuerza de repulsión debido a la radiación emitida por un cuerpo negro a la temperatura T
Datos: masa de la esfera m=0.5 kg, radio rs=5.0 cm, temperaturaT=300 K, distancia entre los centros de las dos esferas, d=10 m
La fuerza es respulsiva
Esta fuerza F es nula para la temperatura Tc
Con los datos anteriores
Fuerza que ejerce la radiación LASER sobre un prisma
Un haz LASER puede ejercer una fuerza apreciable sobre un prisma debido a la refracción (cambio de dirección) de los rayos de luz
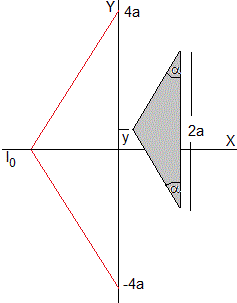
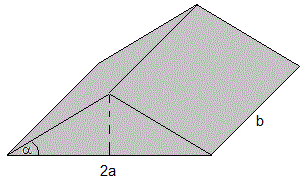
Consideremos un pequeño prisma triangular cuya base es rectangular 2a por b y ángulos adyacentes α=30°, el ángulo del prisma es 180-2α. El índice de refracción del prisma es n y su densidad ρ
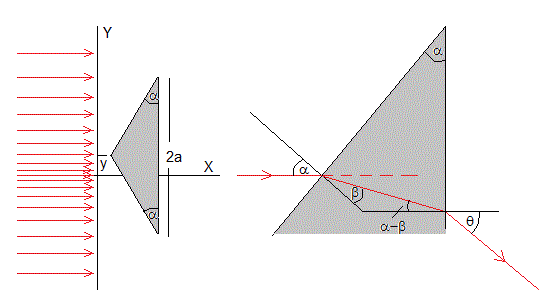
Refracción
Un rayo paralelo al eje X, se refracta en el prisma emergiendo con una dirección θ. Aplicamos dos veces la ley de Snell de la refracción para obtener este ángulo
sinα=n·sinβ
n·sin(α-β)=sinθ
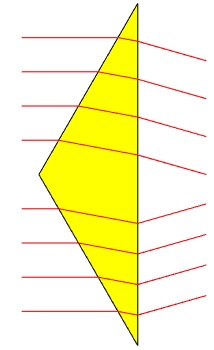
En la figura, se muestra la refracción de algunos de los rayos que inciden sobre el prisma
Supondremos que el índice de refracción del aire es n=1, y que el haz no se refleja en las caras del prisma al estar cubiertas con una sustancia antireflectante
Para dibujar esta figura se ha utilizado el código MATLAB
a=10;
alfa=pi/6;
n=1.5; %índice de refracción
%prisma
h=a/tan(pi/2-alfa);
fill([0,h,h,0],[0,a,-a,0],'y')
%rayos
for y=-a+2:2:a-2
if y==0
continue;
end
x1=sign(y)*y/tan(pi/2-alfa);
line([-1,x1],[y,y],'color','r')%incidente
beta=asin(sin(alfa)/n); %refracción
y1=-tan(alfa-beta)*(h-x1)+y;
line([x1,h], [y,y1],'color','r')
th=asin(n*sin(alfa-beta)); %refracción
x2=h+4;
y2=-sign(y)*tan(th)*(x2-h)+y1;
line([h,x2],[y1,y2],'color','r')
end
axis equal
axis off
Calculamos ahora la variación de momento lineal de un fotón que incide sobre prisma
Mitad superior del prisma
El momento lineal inicial del fotón es
El momento lineal final del fotón es
La variación de momento lineal
Mitad inferior del prisma
El momento lineal inicial del fotón es
El momento lineal final del fotón es
La variación de momento lineal
Energía por unidad de tiempo que ilumina el prisma
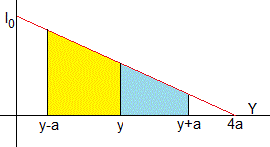
El prisma es iluminado por el haz LASER cuya dirección es el eje X, perpendicular a la base del prisma. La dimensión del haz es 8a por b, la intensidad no es uniforme a lo largo del eje Y sino que disminuye con la distancia a un lado y otro del origen, es máxima I0 en y=0 y nula en y=±4a tal como se muestra en la figura, la intensidad del haz es uniforme a lo largo del eje Z (perpendicular al plano de la figura)
Las ecuaciones de las rectas son
Supongamos que la posición del vértice del prisma es y. Vamos a calcular la energía que recibe la parte superior e inferior del prisma en la unidad de tiempo. Dividiendo esta cantidad por hf tenemos el número de fotones que inciden sobre la parte superior e inferior del prisma en la unidad de tiempo.
Para a≤y≤3a
la energía por unidad de tiempo que incide sobre la parte superior del prisma (color azul claro)
la energía por unidad de tiempo que incide sobre la parte inferior del prisma (color amarillo)
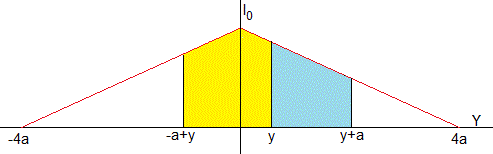
Para 0≤y<a
la energía por unidad de tiempo que incide sobre la parte superior del prisma (color azul claro)
la energía por unidad de tiempo que incide sobre la parte inferior del prisma (color amarillo)
Dividiendo la energía por unidad de tiempo, entre hf obtenemos el número de fotones por unidad de tiempo, multiplicando el resultado por la variación de momento lineal, obtenemos las componentes de la fuerza que ejerce el prisma sobre los fotones
Dividiendo la energía por unidad de tiempo, entre hf obtenemos el número de fotones por unidad de tiempo, multiplicando el resultado por la variación de momento lineal, obtenemos las componentes de la fuerza que ejerce el prisma sobre los fotones
La fuerza que ejerce el haz LASER sobre el prisma es igual y de sentido contario, sus componentes son
Comprobamos que coinciden los valores de Fx y Fy para y=a
Representamos Fx (color rojo) y Fy (color azul) en función de y, en el intervalo -3a≤y≤+3a, tomando a=10 μm. Aprovechamos las propiedades de simetría para calcular solamente la parte derecha de la curva
a=10;
Fx=@(y) (7/4-y.^2/(4*a^2)).*(y<a)+2*(1-y/(4*a)).*(y>=a);
fp=fplot(Fx,[0,3*a]);
x1=fp.XData;
y1=fp.YData;
hold on
plot([-fliplr(x1),x1],[fliplr(y1),y1],'r')
Fy=@(y) -y.*(1-y/(2*a))/(2*a).*(y<a)-(y>=a)/4;
fp=fplot(Fy,[0,3*a]);
x1=fp.XData;
y1=fp.YData;
plot([-fliplr(x1),x1],[-fliplr(y1),y1],'b')
hold off
xlabel('y')
ylabel('F_x, F_y')
grid on
title('Componentes F_x y F_y')
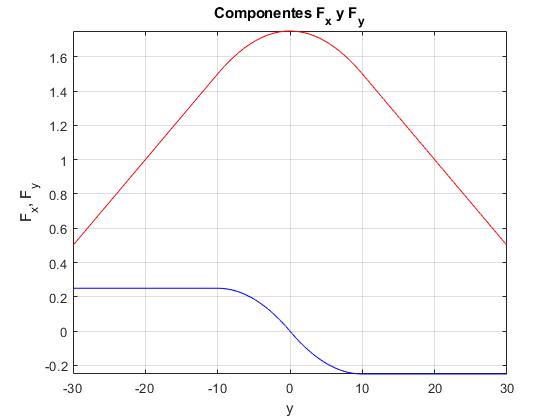
La componente Fy de la fuerza tiene una peculiaridad, la fuerza es de signo contario al desplazamiento y del vértice del prisma, lo que implica un sistema oscilante
Ejemplo
Sea el siguiente prisma
- Angulo adyacente del prisma, α=30°. Angulo del prisma, 180-2·30=120°
- Indice de refracción, n=1.5
- Densidad, ρ=2500 kg/m3
- Dimensiones de la base, a=10 μm, b=1 mm
Conocido el índice de refracción n y el ángulo del prisma α, calculamos el ángulo de desviación θ
sinα=n·sinβ
n·sin(α-β)=sinθ
θ=15.9°
Conocida la densidad ρ y las dimensiones del prisma, calculamos su masa
La masa vale m=1.4434·10-10 kg
Equilibrio
Situamos el vértice del prisma en la posición y=-a/2. La componente Fy de la fuerza que ejerce el haz LASER sobre el prisma es hacia arriba y vale lo mismo que para y=a/2
Determinamos la intensidad máxima I0 para que el prisma esté en equilibrio, es decir, la fuerza Fy se equilibre con el peso mg
I0=8.2571·108 W/m2
Oscilaciones
Supongamos que el mismo experimento se hace en ausencia de gravedad
La ecuación del movimiento del prisma en la región |y|<a
Para oscilaciones de pequeña amplitud, y<<a, hacemos la siguiente aproximación
Se trata de la ecuación diferencial de las oscilaciones libres, con frecuencia angular
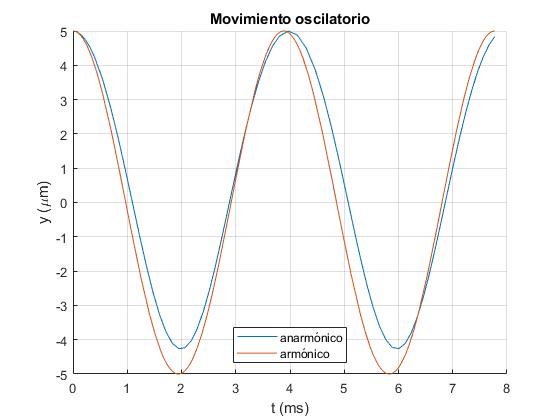
Establecemos un sistema de unidades en el que el tiempo se mide en ms y la distancia en μm. La ecuación del movimiento se escribe
Resolvemos la ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales: en el instante τ=0, Y=A/2, parte del reposo dY/dτ=0, tomamos a=10 μm, A=10
Comparamos esta solución, con la de un movimiento armónico simple de frecuencia angular ω0 o periodo P=2π/ω0 y amplitud A/2
a=10e-6; %dimensiones
b=1e-3;
n=1.5; %indice de refracción
rho=2500; %densidad
alfa=pi/6; %ángulo del prisma (adyacente)
m=rho*a^2*b*tan(alfa); %masa
beta=asin(sin(alfa)/n);
th=asin(sin(alfa-beta)*n); %ángulo desviación
y=a/2; %equilibrio
I0=4*m*9.8*a*3e8/(b*y*(2*a-y)*sin(th)); %intensidad máxima
%oscilaciones
w2=b*I0*sin(th)*1e-6/(2*m*3e8);
periodo=2*pi/sqrt(w2);
A=10; % y en micrometros, t en milisegundos
f=@(t,x) [x(2); -w2*x(1)*(1-x(1)/(2*A))];
[t,x]=ode45(f,[0,2*periodo],[A/2,0]);
hold on
plot(t, x(:,1))
fplot(@(t) A*cos(sqrt(w2)*t)/2,[0,2*periodo])
hold off
grid on
legend('anarmónico','armónico','location','south')
xlabel('t (ms)')
ylabel('y (\mum)')
title('Movimiento oscilatorio')
Referencias
Lim Yung-kuo. Problems and Solutions on Mechanics. World Scientific (1994). Problem 1037, pp. 51-53
IPhO Problems and Solutions. Problem 2, Laser forces on a transparent prism. 1993, USA
Indian Olympiad Qualifer in Astronomy (IOQA) - 2021-2022. Part II: Indian National Astronomy Olympiad (INAO). Homi Bhabha Centre for Science Education (HBCSE-TIFR), 20 March 2022, problem 2

