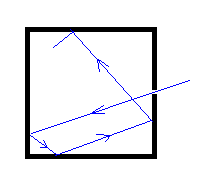
La superficie de un cuerpo negro es un caso límite, en el que toda la energía incidente desde el exterior es absorbida y toda la energía incidente desde el interior es emitida.

No existe en la naturaleza un cuerpo negro, incluso el negro de humo refleja el 1% de la energía incidente.

Sin embargo, un cuerpo negro se puede sustituir con gran aproximación por una cavidad con una pequeña abertura. La energía radiante incidente a través de la abertura, es absorbida por las paredes en múltiples reflexiones y solamente una mínima proporción escapa (se refleja) a través de la abertura.

Consideremos una cavidad cuyas paredes están a una cierta temperatura. Los átomos que componen las paredes están emitiendo radiación electromagnética y al mismo tiempo absorben la radiación emitida por otros átomos de las paredes. Cuando la radiación encerrada dentro de la cavidad alcanza el equilibrio con los átomos de las paredes, la cantidad de energía que emiten los átomos en la unidad de tiempo es igual a la que absorben. En consecuencia, la densidad de energía del campo electromagnético existente en la cavidad es constante.

A cada frecuencia corresponde una densidad de energía que depende solamente de la temperatura de las paredes y es independiente del material del que están hechas.

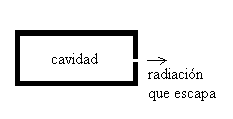
Si se abre un pequeño agujero en el recipiente, parte de la radiación se escapa y se puede analizar. El agujero se ve muy brillante cuando el cuerpo está a alta temperatura y se ve completamente negro a bajas temperaturas.

Históricamente, el nacimiento de la Mecánica Cuántica, se sitúa en el momento en el que Max Panck explica el mecanismo que hace que los átomos radiantes produzcan la distribución de energía observada. Max Planck sugirió en 1900 que

1. La radiación dentro de la cavidad está en equilibrio con los átomos de las paredes que se comportan como osciladores armónicos de frecuencia dada f.
2. Cada oscilador puede absorber o emitir energía de la radiación en una cantidad proporcional a f. Cuando un oscilador absorbe o emite radiación electromagnética, su energía aumenta o disminuye en una cantidad hf.

La segunda hipótesis de Planck, establece que la energía de los osciladores está cuantizada. La energía de un oscilador de frecuencia f sólo puede tener ciertos valores que son 0, hf, 2hf ,3hf ....nhf .

La distribución espectral de radiación es continua y tiene un máximo dependiente de la temperatura. La distribución espectral se puede expresar en términos de la longitud de onda o de la frecuencia de la radiación.

dE_f /df es la densidad de energía por unidad de frecuencia para la frecuencia f de la radiación contenida en una cavidad a la temperatura absoluta T. Su unidad es (J·m^-3)·s.

${\displaystyle \frac{d{E}_f}{df}=\frac{8\pi h}{c^3}\frac{f^3}{\exp \left(hf/kT\right)-1}}$

donde k es la constante de Boltzmann cuyo valor es k=1.3805·10^-23 J/K.

dE_λ /dλ es la densidad de energía por unidad de longitud de onda para la longitud de onda λ de la radiación contenida en una cavidad a la temperatura absoluta T. Su unidad es (J·m^-3)·m^-1.

${\displaystyle \begin{array}{l}f=\frac{c}{\lambda }\frac{df}{d\lambda }=-\frac{c}{{\lambda }^2}\\ \frac{d{E}_{\lambda }}{d\lambda }=-\frac{d{E}_f}{df}\frac{df}{d\lambda }=\frac{8\pi hc}{{\lambda }^5}\frac{1}{\exp \left(hc/\lambda kT\right)-1}\end{array}}$

La intensidad (energía por unidad de área y unidad de tiempo) por unidad de longitud de onda para la longitud de onda λ, de un cuerpo negro a la temperatura absoluta T, viene dada por la expresión.

${\displaystyle \frac{d{W}_{\lambda }}{d\lambda }=\frac{2\pi h{c}^2}{{\lambda }^5}\frac{1}{\exp \left(hc/\lambda kT\right)-1}}$

Su unidad es (W·m^-2)·m^-1.

La intensidad (energía por unidad de área y unidad de tiempo) por unidad de frecuencia para la frecuencia f, de un cuerpo negro a la temperatura absoluta T, viene dada por la expresión.

${\displaystyle \frac{d{W}_f}{df}=\frac{2\pi h}{c^2}\frac{f^3}{\exp \left(hf/kT\right)-1}}$

Su unidad es (W·m^-2)·s.

Representamos gráficamente esta función en escala doblemente logarítmica para varias temperaturas. La intensidad por unidad de frecuencia en el eje vertical y la frecuencia en el eje horizontal. El intervalo de frecuencias de la representación gráfica (de la figura) es 10¹¹ a 10¹⁶ Hz.

Datos: h=6.6256·10^-34, k=1.3805·10^-23, c=2.9979·10⁸.

h=6.6256e-34;
k=1.3805e-23;
c=2.9979e8;
f=@(x,T) ((2*pi*h/c^2)*x.^3)./(exp(h*x/(k*T))-1);
T=[500 1000 2000 5000 10000];
col=['b' 'g' 'r' 'm' 'k'];
x=linspace(11,16,50);
hold on
for i=1:length(T)
    y=log10(f(10.^x,T(i)));
    plot(x,y, col(i),'displayName',num2str(T(i)))
end
axis([11 16 -13 -6]);
title('Ley del desplazamiento de Wien')
xlabel('Frecuencia')
ylabel('Intensidad por u. de frecuencia')
legend('-DynamicLegend','location','northwest')
hold off

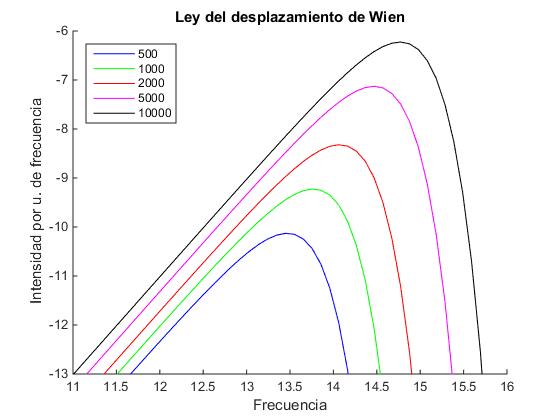
La ley del desplazamiento de Wien

La posición del máximo en el espectro de la radiación del cuerpo negro depende de la temperatura del cuerpo negro y está dado por la ley de desplazamiento de Wien. Calculando la derivada primera de la función de la distribución de Planck expresada en términos de la longitud de onda o de la frecuencia

${\displaystyle \frac{d}{d\lambda }\left(\frac{1}{{\lambda }^5}\frac{1}{\exp \left(hc/\lambda kT\right)-1}\right)=0}$

Obtenemos la ecuación trascendente

${\displaystyle 5(e^x-1)-x{e}^x=0x=\frac{hc}{\lambda {}_{m}kT}=4.965}$

Este resultado constituye la ley de desplazamiento de Wien, que establece que el máximo de la densidad de energía dE_λ /dλ por unidad de longitud de onda a distintas temperaturas T₁, T₂, T₃, .., se produce a las longitudes de onda λ₁, λ₂, λ₃...tales que

${\displaystyle {\lambda }_1{T}_1={\lambda }_2{T}_2={\lambda }_3{T}_3=\mathrm{...}=\frac{hc}{k4.965}=2.898·{10}^{-3}\text{m·K}}$

De modo similar en el dominio de las frecuencias

${\displaystyle \frac{d}{df}\left(\frac{f^3}{\exp \left(hf/kT\right)-1}\right)=0}$

Obtenemos la ecuación trascendente

${\displaystyle 3(e^x-1)-x{e}^x=0x=\frac{h{f}_m}{kT}=2.822}$

A medida que la temperatura T se incrementa, el máximo se desplaza hacia longitudes de onda menores (mayores frecuencias).

El producto

λ_m·f_m=0.5684·c.

En la ventana de comandos definimos las funciones

${\displaystyle \begin{array}{l}y=x-5\left(1-e^{-x}\right)\\ y=x-3\left(1-e^{-x}\right)\end{array}}$

calculamos la raíz de cada una de ellas empleando la función MATLAB fzero

>> f=@(x) x-5*(1-exp(-x));
>> fzero(f,4.5)
ans =
    4.9651
>> f=@(x) x-3*(1-exp(-x));
>> fzero(f,3.0)
ans =
    2.8214

La ley de Stefan-Boltzmann

La intensidad total en W·m^-2, de la radiación emitida por un cuerpo negro, se obtiene integrando la expresión anterior para todas las longitudes de onda (o frecuencias).

${\displaystyle \begin{array}{l}{W}_f=\frac{2\pi h}{c^2}{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{f^3}{\exp (hf/kT)-1}df,x=\frac{hf}{kT}}\\ W_f=\frac{2\pi k^4{T}^4}{c^2{h}^3}{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{x^3}{e^x-1}dx}=\frac{2\pi k^4{T}^4}{c^2{h}^3}\frac{{\pi }^4}{15}=\frac{2{\pi }^5{k}^4}{15c^2{h}^3}{T}^4=\sigma T^4\\ W_{\lambda }=2\pi h{c}^2{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{1}{{\lambda }^5}\frac{1}{\exp (hc/\lambda kT)-1}d\lambda },x=\frac{hc}{\lambda kT}\\ W_{\lambda }=-\frac{2\pi k^4{T}^4}{c^2{h}^3}{\displaystyle \underset{\infty }{\overset{0}{\int }}\frac{x^3}{e^x-1}dx}=\frac{2{\pi }^5{k}^4}{15c^2{h}^3}{T}^4=\sigma T^4\end{array}}$

con σ =5.670·10^-8 (Wm^-2K^-4)

Esta expresión se conoce como ley de Stefan-Boltzmann. La energía emitida por un cuerpo negro por unidad de área y unidad de tiempo es proporcional a la cuarta potencia de la temperatura absoluta T.

>> syms x;
>> int(x^3/(exp(x)-1),0,inf)
ans =pi^4/15

Intensidad de la radiación emitida en una región del espectro

Vamos a calcular, la intensidad emitida por un cuerpo negro en una región del espectro comprendida entre las frecuencias f₁ y f₂, o entre las longitudes de onda λ₁=c/f₁ y λ₂=c/f₂

La fracción de la intensidad emitida en una región del espectro es el cociente entre la intensidad emitida en dicha región dividido por la intensidad total (ley de Stefan).

${\displaystyle \begin{array}{l}F(f_1,f_2)=\frac{\frac{2\pi k^4{T}^4}{c^2{h}^3}{\displaystyle \underset{x_1}{\overset{x_2}{\int }}\frac{x^3}{e^x-1}dx}}{\frac{2{\pi }^5{k}^4}{15c^2{h}^3}{T}^4}=\frac{15}{{\pi }^4}{\displaystyle \underset{x_1}{\overset{x_2}{\int }}\frac{x^3}{e^x-1}dx}\text{,}x=\frac{hf}{kT}\\ F({\lambda }_1,{\lambda }_2)=-\frac{15}{{\pi }^4}{\displaystyle \underset{x_1}{\overset{x_2}{\int }}\frac{x^3}{e^x-1}dx},x=\frac{hc}{\lambda kT}\end{array}}$

Esta fracción no depende de λ o de T sino del producto λT. Esto quiere decir que por ejemplo la fracción de la intensidad emitida por un cuerpo negro en la región del espectro comprendida entre 0 y 10 μm a 1000º K es la misma que la fracción de la intensidad emitida en la región comprendida entre 0 y 5 μm a 2000º K.

Otra forma de expresar la inetgral definida

${\displaystyle \begin{array}{l}F(f_1,f_2)=\frac{15}{{\pi }^4}{\displaystyle \underset{x_1}{\overset{x_2}{\int }}\frac{x^3}{e^x-1}dx}=\frac{15}{{\pi }^4}\left\{{\displaystyle \underset{x_1}{\overset{\infty }{\int }}\frac{x^3}{e^x-1}dx}-{\displaystyle \underset{x_2}{\overset{\infty }{\int }}\frac{x^3}{e^x-1}dx}\right\}=\frac{15}{{\pi }^4}\left\{F(x_1)-F(x_2)\right\}\\ F(x)={\displaystyle \underset{x}{\overset{\infty }{\int }}\frac{x^3}{e^x-1}dx}\end{array}}$

El integrando es el producto

${\displaystyle \frac{x^3}{e^x-1}=x^3{e}^{-x}\frac{1}{1-e^{-x}}}$

El último término, es la suma de los infinitos términos de la progresión geométrica

${\displaystyle \begin{array}{l}\mathrm{1,}{e}^{-x},e^{-2x},e^{-3x}\mathrm{,...,}{e}^{-nx}\\ S_n={\displaystyle \sum _{n=0}^n{e}^{-nx}}=\frac{1-e^{-(n+1)x}}{1-e^{-x}}\\ \underset{n\to \infty }{\lim }{S}_n=\frac{1}{1-e^{-x}}\end{array}}$

La integral es la suma de infinitas integrales

${\displaystyle \begin{array}{l}\frac{x^3}{e^x-1}=x^3{e}^{-x}\frac{1}{1-e^{-x}}=x^3{e}^{-x}{\displaystyle \sum _{n=0}^{\infty }{e}^{-nx}}=x^3{\displaystyle \sum _{n=0}^{\infty }{e}^{-(n+1)x}}\\ {\displaystyle \underset{x}{\overset{\infty }{\int }}\frac{x^3}{e^x-1}dx={\displaystyle \underset{x}{\overset{\infty }{\int }}{x}^3\left({\displaystyle \sum _{n=0}^{\infty }{e}^{-(n+1)x}}\right)dx}}={\displaystyle \sum _{n=0}^{\infty }{\displaystyle \underset{x}{\overset{\infty }{\int }}{x}^3{e}^{-(n+1)x}}dx}\end{array}}$

Integramos tres veces por partes

${\displaystyle \begin{array}{l}{\displaystyle \int x^3{e}^{-(n+1)x}dx}\{\begin{array}{l}u=x^3,du=3x^{2}dx\\ dv=e^{-(n+1)x}dx,v=-\frac{e^{-(n+1)x}}{n+1}\end{array}\\ -\frac{e^{-(n+1)x}}{n+1}{x}^3+\frac{3}{n+1}{\displaystyle \int x^2{e}^{-(n+1)x}dx}\{\begin{array}{l}u=x^2,du=2x·dx\\ dv=e^{-(n+1)x}dx,v=-\frac{e^{-(n+1)x}}{n+1}\end{array}\\ -\frac{e^{-(n+1)x}}{n+1}{x}^3+\frac{3}{n+1}\left\{-\frac{e^{-(n+1)x}}{n+1}{x}^2+\frac{2}{n+1}{\displaystyle \int x{e}^{-(n+1)x}dx}\right\}\{\begin{array}{l}u=x,du=dx\\ dv=e^{-(n+1)x}dx,v=-\frac{e^{-(n+1)x}}{n+1}\end{array}\\ -\frac{e^{-(n+1)x}}{n+1}{x}^3+\frac{3}{n+1}\left\{-\frac{e^{-(n+1)x}}{n+1}{x}^2+\frac{2}{n+1}\left\{-\frac{e^{-(n+1)x}}{n+1}x+\frac{1}{n+1}{\displaystyle \int e^{-(n+1)x}dx}\right\}\right\}=\\ -\frac{e^{-(n+1)x}}{n+1}{x}^3+\frac{3}{n+1}\left\{-\frac{e^{-(n+1)x}}{n+1}{x}^2+\frac{2}{n+1}\left\{-\frac{e^{-(n+1)x}}{n+1}x-\frac{e^{-(n+1)x}}{{\left(n+1\right)}^2}\right\}\right\}=\\ -\frac{e^{-(n+1)x}}{n+1}\left\{x^3+\frac{3x^2}{n+1}+\frac{6x}{{\left(n+1\right)}^2}+\frac{6}{{\left(n+1\right)}^3}\right\}\end{array}}$

Evaluamos el término n de la la integral entre el límite inferior y superior, x e ∞

${\displaystyle \begin{array}{l}{\displaystyle \underset{x}{\overset{\infty }{\int }}{x}^3{e}^{-(n+1)x}}dx={-\frac{e^{-(n+1)x}}{n+1}\left\{x^3+\frac{3x^2}{n+1}+\frac{6x}{{\left(n+1\right)}^2}+\frac{6}{{\left(n+1\right)}^3}\right\}|}_x^{\infty }=\\ =\frac{e^{-(n+1)x}}{n+1}\left\{x^3+\frac{3x^2}{n+1}+\frac{6x}{{\left(n+1\right)}^2}+\frac{6}{{\left(n+1\right)}^3}\right\}\end{array}}$

El resultado final es

${\displaystyle \begin{array}{l}F(x)={\displaystyle \underset{x}{\overset{\infty }{\int }}\frac{x^3}{e^x-1}dx}={\displaystyle \sum _{n=0}^{\infty }{\displaystyle \underset{x}{\overset{\infty }{\int }}{x}^3{e}^{-(n+1)x}}dx}={\displaystyle \sum _{n=0}^{\infty }\frac{e^{-(n+1)x}}{n+1}\left\{x^3+\frac{3x^2}{n+1}+\frac{6x}{{\left(n+1\right)}^2}+\frac{6}{{\left(n+1\right)}^3}\right\}=}\\ {\displaystyle \sum _{n=1}^{\infty }\frac{e^{-nx}}{n}\left\{x^3+\frac{3x^2}{n}+\frac{6x}{n^2}+\frac{6}{n^3}\right\}}\end{array}}$

Probamos que es una serie convergente

${\displaystyle \begin{array}{l}\underset{n\to \infty }{\lim }\left|\frac{S_{n+1}}{S_n}\right|<1\\ \frac{S_{n+1}}{S_n}=\frac{\frac{e^{-(n+1)x}}{n+1}\left\{x^3+\frac{3x^2}{n+1}+\frac{6x}{{\left(n+1\right)}^2}+\frac{6}{{\left(n+1\right)}^3}\right\}}{\frac{e^{-nx}}{n}\left\{x^3+\frac{3x^2}{n}+\frac{6x}{n^2}+\frac{6}{n^3}\right\}}=\frac{n}{n+1}{e}^{-x}\frac{x^3+\frac{3x^2}{n+1}+\frac{6x}{{\left(n+1\right)}^2}+\frac{6}{{\left(n+1\right)}^3}}{x^3+\frac{3x^2}{n}+\frac{6x}{n^2}+\frac{6}{n^3}}\\ \underset{n\to \infty }{\lim }\left|\frac{S_{n+1}}{S_n}\right|=\frac{1}{e^x}\end{array}}$

Como x>0, el cociente es menor que la unidad

En vez de intervalos de frecuencias se suele utilizar intervalos de longitudes de onda

${\displaystyle \begin{array}{l}F({\lambda }_1,{\lambda }_2)=\frac{15}{{\pi }^4}\left\{F(x_2)-F(x_1)\right\},x=\frac{hc}{\lambda kT}\\ F(x)={\displaystyle \sum _{n=1}^{\infty }\frac{e^{-nx}}{n}\left\{x^3+\frac{3x^2}{n}+\frac{6x}{n^2}+\frac{6}{n^3}\right\}}\end{array}}$

Calcularemos la intensidad de la radiación emitida por un cuerpo negro a una temperatura dada en distintos intervalos de longitudes de onda. En la tabla se recogen los datos de las distintas regiones del espectro, la longitud de onda se da en μm (10^-6 m).

Fuente: Alonso M, Finn E. Campos y Ondas. Fondo Educativo Interamericano (1970), págs 791-792

Creamos un script en el que se establece mediante el comando input:

• La temperatura (K)
• El límite inferior de la longitud de onda en μm (10^-6 m) de la región del espectro elegida (ver tabla)
• El límite superior de la longitud de onda en μm (10^-6 m) de la región del espectro elegida

Utiliza la función MATLAB integral para calcular la integral definida, o la función F(x) emplenado 100 términos del desarrollo en serie

Imprime el resultado: proporción (tanto por ciento) e intensidad W/m²

Datos: h=6.6256·10^-34, k=1.3805·10^-23, c=2.9979·10⁸.

lambda1=input('límite inferior micrómetros): ');
lambda2=input('límite superior micrómetros): ');
T=input('Temperatura (K): ');
h=6.6256e-34;
k=1.3805e-23;
c=2.9979e8;
a=h*c/(lambda1*1e-6*k*T);
b=h*c/(lambda2*1e-6*k*T);
%integral definida
f=@(x) (x.^3)./(exp(x)-1);
res=-integral(f,a,b)*15/pi^4; 
fprintf('proporción : %2.3f\n',res*100)
%serie
n=1:100;
F=@(x) sum((exp(-n*x).*(x^3+(3*x^2)./n+(6*x)./n.^2+6./n.^3))./n);
res1=(F(b)-F(a))*15/pi^4;
fprintf('proporción : %2.3f\n',res1*100)

En la ventana de comandos, obtenemos para el infrarrojo (0.78 a 1000 µm) a la temperatura de 5000 K, el tanto por ciento 53.761% de la intensidad emitida en dicha región del espectro, es decir, el cociente entre la intensidad emitida en dicha región, dividido por la intensidad total (ley de Stefan), multiplicando el resultado por cien

límite inferior micrómetros): 0.78
límite superior micrómetros): 1000
Temperatura (K): 5000
proporción : 53.761
proporción : 53.761

Obtenemos los mismos resultados empleando el procedimiento integral de MATLAB o el desarrollo en serie tomando 100 términos

En la siguiente tabla, se proporcionan los datos acerca del tanto por ciento de la contribución de la radiación infrarroja, visible y ultravioleta a la radiación de un cuerpo negro a las temperaturas 1000, 2000, 3000, ..., 10 000 K.

function negro_2
    k=1.3805e-23;
    c=2.9979e8;
    h=6.6256e-34;
    for T=1000:1000:10000
        %infrarrojo
        resIr=ciento(0.78, 1000, T)*100;
        %visible
        resVi=ciento(0.38, 0.78, T)*100;      
        %ultravioleta
        resUv=ciento(0.006, 0.38, T)*100;
        fprintf('T: %5i,  Ir: %2.3f,  Vi: %2.3f,  Uv: %2.3f\n',T, resIr, 
resVi, resUv)
    end
        
    function res=ciento(lambda1, lambda2, T)
        a=h*c/(lambda1*1e-6*k*T);
        b=h*c/(lambda2*1e-6*k*T);
        %integral
        %f=@(x) (x.^3)./(exp(x)-1);
        %res=-integral(f,a,b)*15/pi^4;
        %serie
        n=1:100;
        F=@(x) sum((exp(-n*x).*(x^3+(3*x^2)./n+(6*x)./n.^2+6./n.^3))./n);
        res=(F(b)-F(a))*15/pi^4;
    end
end

T:  1000,  Ir: 99.999,  Vi: 0.001,  Uv: 0.000
T:  2000,  Ir: 98.326,  Vi: 1.673,  Uv: 0.001
T:  3000,  Ir: 87.201,  Vi: 12.668,  Uv: 0.131
T:  4000,  Ir: 69.976,  Vi: 28.617,  Uv: 1.407
T:  5000,  Ir: 53.761,  Vi: 41.029,  Uv: 5.210
T:  6000,  Ir: 40.919,  Vi: 47.472,  Uv: 11.610
T:  7000,  Ir: 31.330,  Vi: 49.030,  Uv: 19.640
T:  8000,  Ir: 24.279,  Vi: 47.496,  Uv: 28.225
T:  9000,  Ir: 19.079,  Vi: 44.323,  Uv: 36.598
T: 10000,  Ir: 15.204,  Vi: 40.461,  Uv: 44.335

• A baja temperatura prácticamente toda la radiación es infrarroja.
• A muy alta temperatura la contribución de la radiación ultravioleta es cada vez mayor y la visible e infrarroja se hacen cada vez menores.
• La contribución de la radiación visible alcanza un máximo aproximadamente a 7100º K.

Veamos ahora, la explicación del color aparente de un cuerpo caliente. Por ejemplo, a temperatura de 2000 K un cuerpo emite luz visible pero la intensidad en el extremo rojo (baja frecuencia, alta longitud de onda) del espectro visible es mucho mayor que la azul (alta frecuencia, baja longitud de onda) y el cuerpo aparece rojo brillante. A 3000 K, la temperatura aproximada de un filamento de una lámpara incandescente, la cantidad relativa de luz azul ha aumentado, pero predomina aún la componente roja. A 6000 K, que es aproximadamente la temperatura del Sol, la distribución es casi uniforme entre todas las componentes de la luz visible y el cuerpo aparece blanco brillante. Por encima de 10000 K se emite luz azul con mayor intensidad que roja y un cuerpo (estrella caliente) a esta temperatura se ve azul.

Actividades

Se introduce

• La temperatura (K), en el control titulado Temperatura
• La región del espectro, en el control titulado Región del espectro. En los controles titulados longitudes de onda desde ... hasta ... se proporcionan los datos del intervalo de longitudes de onda en μm (10^-6 m) de dicha región.

Se pulsa el botón titulado Nuevo.

En la parte superior derecha, se muestra el valor calculado de la intensidad en W/m² y muestra la fracción (tanto por ciento) de la intensidad de la radiación emitida en la región del espectro seleccionada.

La temperatura del Sol

Para determinar la temperatura de la radiación de un cuerpo negro o de una estrella de la misma temperatura se mide la longitud de onda λ_m a la cual el cuerpo negro emite con intensidad máxima. Aplicando la ley de Wien

λ_m·T=2.898·10^-3 m·K

se determina la temperatura de dicho cuerpo. Por ejemplo, si el máximo está en la longitud de onda λ_m=0.5·10^-6 m, la temperatura del cuerpo negro es de 5800 K, tal como se muestra en la figura.

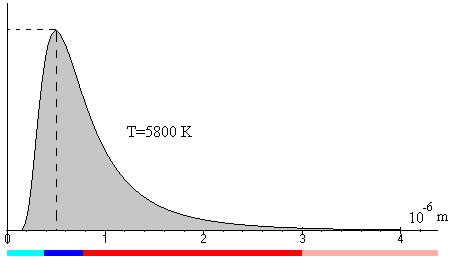
La radiación Sol es absorbida por la atmósfera de la Tierra, por lo que no es fácil determinar la longitud de onda a la cual se produce la máxima intensidad.

Otra forma de medir la temperatura del Sol, es la aplicación de la ley de Stefan-Boltzmann. La energía emitida por unidad de tiempo en todo el espectro por un cuerpo negro a la temperatura T es

P=σAT⁴

donde A es el área de la superficie del cuerpo. La temperatura T efectiva del Sol será la de un cuerpo negro de la misma área A que emita la energía P por unidad de tiempo del Sol.

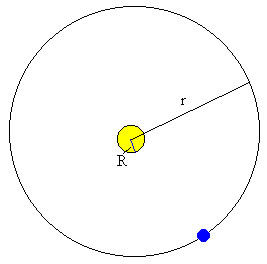
Supongamos que el Sol es una esfera de radio R y medimos la intensidad de la radiación solar a una distancia r del centro del Sol, por ejemplo en la Tierra.

La energía emitida por el Sol, supuesto un cuerpo negro a la temperatura T es

P=4πR²σT⁴

Si suponemos que el Sol emite en todas las direcciones de forma isótropa. La intensidad de la radicación solar a una distancia r del centro del Sol es

${\displaystyle I=\frac{P}{4\pi r^2}=\sigma T^4\frac{R^2}{r^2}}$

Datos:

• Constante de Stefan-Boltzmann, σ=5.67·10^-8 (Wm^-2K^-4).
• Radio del Sol, R=6.96·10⁸ m
• Distancia entre la Tierra y el Sol, r=1.49·10¹¹ m.
• Intensidad de la radiación solar medida en la órbita de la Tierra, I=1390 W/m²

Lo que nos da una temperatura T=5790 K o del orden de 6000 K.

Intensidad de la radiación solar medida en la órbita de la Tierra se denomina constante solar y el valor que aparece en muchos textos es de 1367 W/m²

Representamos la intensidad (energía por unidad de área y unidad de tiempo) por unidad de longitud de onda para la longitud de onda λ, de un cuerpo negro a la temperatura absoluta T=6000 K, según la primera expresión de esta página.

${\displaystyle \frac{d{W}_{\lambda }}{d\lambda }=\frac{2\pi h{c}^2}{{\lambda }^5}\frac{1}{\exp \left(hc/\lambda kT\right)-1}}$

Su unidad es (W·m^-2)·m^-1.

h=6.6256e-34;
k=1.3805e-23;
c=2.9979e8;
T=6000;
f=@(x) ((2*pi*h*c^2*1.0e30)./x.^5)./(exp((1.0e6*h*c)./(x*k*T))-1);
T=6000;
fplot(f,[0.25,4])
grid on
title('Cuerpo negro')
xlabel('Longitud de onda \mum')
ylabel('W·m^-^2 \mum^-^2')

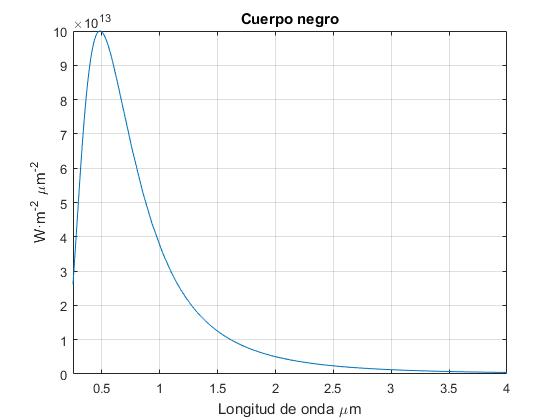
A la temperatura de 6000 K, el 47.7% de la intensidad de la radiación emitida por el Sol se encuentra en la región visible del espectro, de 0.78 (rojo) a 0.38 (violeta) micrómetros. Dividimos el área bajo la curva en la región del espectro visible entre el área total bajo la curva

>> integral(f,0.38,0.78)/integral(f,0,inf)
ans =    0.4747

O bien, utilizando el script del apartado anterior

límite inferior micrómetros): 0.78
límite superior micrómetros): 0.38
Temperatura (K): 6000
proporción : 47.5
intensidad (W/m2): 34879007.1

Dado que la órbita de la Tierra es ligeramente elíptica (excentricidad ε=0.017), la intensidad de la radiación que nos llega del Sol es máxima en el perihelio r₁=a(1-ε) y mínima en el afelio r₂=a(1+ε). Donde a es el semieje mayor de la elipse 1.496·10¹¹ m

Espectro ASTM G173-03. Air mass 1.5

A medida que la radiación procedente del Sol atraviesa la atmósfera, es absorbida, reflejada y difundida. Debido a estos procesos, la intensidad de a radiación que nos llega a la superficie de la Tierra es menor: la reducción es del orden del 30% por ciento en un día claro y del orden del 90% en un día cubierto

La radiación directa es la que nos viene directamente del disco solar y la radiación difusa es la que viene de cualquier otra dirección. En un día claro la mayor parte de la radiación que alcanza la superficie terreste es directa, vemos claramente la sombra de los objetos. En un día cubierto, la componente directa de la radiación solar es muy pequeña y los objetos no producen sombra. La radiación global es la suma de ambas contribuciones

La radiación difusa se origina por la interacción de las ondas electromagnéticas con las moléculas de nitrógeno, oxígeno, vapor de agua, gotas de agua y de polvo en suspensión en la atmósfera.

La radiación es absorbida por el ozono, el vapor de agua y el anhídrido de carbono, experimenta la denominada dispersión (scattering) Rayleigh por el polvo y el agua. El ozono absorbe radiación en la zona ultravioleta del espectro <0.3 micrómetros, el vapor de agua y el CO₂, en la zona infrarroja.

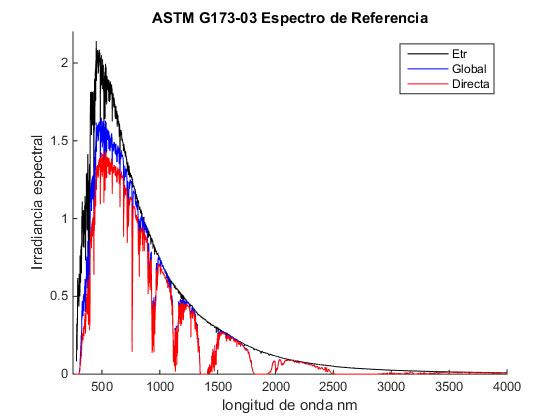
El espectro ASTM G173 nos proporciona la potencia (vatios por metro cuadrado por nanómetro de ancho de banda) en función de la longitud de onda bajo unas condiciones atmósféricas especificadas en el documento Reference Solar Spectral Irradiance: Air Mass 1.5.

La tabla se descarga directamente desde el enlace http://rredc.nrel.gov/solar/spectra/am1.5/ASTMG173.html. Con el botón derecho del ratón se selecciona la opción Guardar como... El documento se abre con Word Pad, se elimina las dos líneas de la cabecera y se guarda como documento de texto, extensión .TXT. El fichero se puede descargar en este enlace espectro.txt

Se coloca el fichero espectro.txt en una carpeta accesible por MATLAB y se selecciona File/Import data y en el asistente a la importación de datos, Import Wizard, vemos cuatro columnas de datos.

La primera columna es la longitud de onda en nanómetros nm (10^-9 m)

Las otras tres columnas miden la Irradiancia Espectral en W m^-2nm^-1:

1. Extraterreste
2. Global total
3. Normal directa

Creamos un script para importar los datos mediante el comando load y reproducir la figura que aparece enla página de dicho documento

load espectro.txt
 hold on
 plot(espectro(:,1), espectro(:,2),'k')
 plot(espectro(:,1), espectro(:,3),'b')
 plot(espectro(:,1), espectro(:,4),'r')
 xlim([250,4000])
 ylim([0 2.2])
 xlabel('longitud de onda nm')
 ylabel('Irradiancia espectral')
 legend('Etr','Global','Directa')
 title('ASTM G173-03 Espectro de Referencia')

Referencias

C Calcaneo-Roldan, O Salcido, D Santana. A semi-analytical approach to black body radiation. Eur. J. Phys. 38 (2017) 055807