La curva cicloide

La cicloide se produce cuando se hace rodar sin deslizar un disco sobre una superficie horizontal. Un punto del borde del disco describe una curva que se denomina cicloide (palabra griega que significa circular). A un giro del disco le corresponde un arco de la cicloide

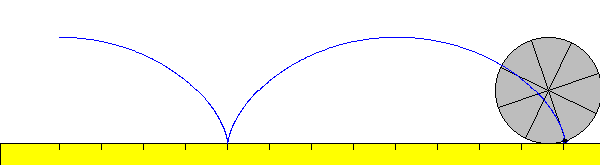
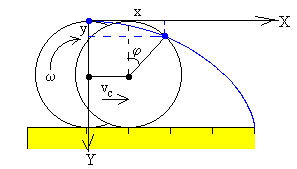
Si el punto P en el instante inicial está en la parte superior del disco, al cabo de un cierto tiempo t las coordenadas del punto P serán, tal como se muestra en la figura

x=v_c·t+R·sinφ y=R-R·cosφ

donde R es el radio del círculo y φ el ángulo girado en el tiempo t, φ=ω·t.

La relación entre la velocidad de traslación del centro de masas v_c y de rotación ω alrededor de un eje que pasa por el centro de masa es v_c=ω ·R.

La ecuaciones paramétricas de la cicloide son

x=R(φ+sinφ)
y=R(1-cosφ )

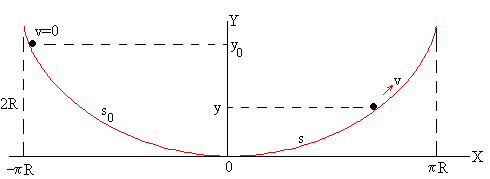
Cuando φ=0, x=0, y=0, cuando φ=π, x=πR, y=2R, cuando φ=-π, x=-πR, y=2R,

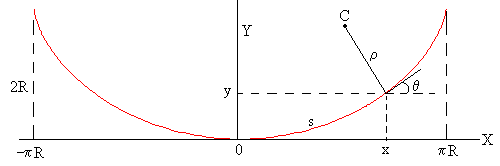
La cicloide es simétrica, por lo que situamos el eje Y como eje de simetría, y el origen en la parte más baja de la curva, tal como se muestra en la figura. La ecuación de la cicloide referida a estos ejes es

x=R(φ+sinφ)
y=R(1-cosφ)

Cuando φ=-π, x=-πR, y=2R, cuando φ=π, x=πR, y=2R,

Donde R y φ son dos parámetros

La pendiente de la cicloide en la posición x es

${\displaystyle \tan \theta =\frac{dy}{dx}=\frac{R\sin \phi ·d\phi }{R(1+\cos \phi )\text{·}d\phi }=\frac{2\sin \left(\frac{\phi }{\text{2}}\right)\cos \left(\frac{\phi }{\text{2}}\right)}{2{\cos }^2\left(\frac{\phi }{\text{2}}\right)}=\tan \left(\frac{\phi }{\text{2}}\right)}$

El parámetro φ tiene un significado geométrico, φ/2 es la pendiente θ de la recta tangente a la cicloide.

Escribimos las ecuaciones paramétricas de la cicloide de forma alternativa

x=R(2θ+sin(2θ))
y=R(1-cos(2θ))

Calculamos ahora la longitud del arco s, entre el origen y el punto de coordenadas (x, y)

${\displaystyle \begin{array}{l}d{s}^2=d{x}^2+d{y}^2=\left(4R^2{(1+\cos (2\theta ))}^2+4R^2{\sin }^2(2\theta )\right){\left(d\theta \right)}^2=16R^2{\cos }^2\theta ·{\left(d\theta \right)}^2\\ ds=4R\cos \theta ·d\theta \\ s={\displaystyle \underset{0}{\overset{\theta }{\int }}4R\cos \theta ·d\theta =4R\sin \theta }\end{array}}$

La longitud de medio arco, es decir, del arco entre el origen (0, 0) y el extremo (πR, 2R) es

${\displaystyle s={\displaystyle \underset{0}{\overset{\pi /2}{\int }}4R\cos \theta ·d\theta =4R}}$

La trayectoria de un punto situado en el borde de una rueda de radio R que rueda sin deslizar es una cicloide. Sin embargo, el radio de curvatura de la cicloide en la posición (x, y) no es constante sino

${\displaystyle \rho =\frac{ds}{d\theta }=4R\cos \theta }$

Movimiento a lo largo de una cicloide (sin rozamiento)

Establecemos el mismo origen y ejes para describir el movimiento sobre la cicloide

La cicloide es simétrica, por lo que situamos el eje Y como eje de simetría, y el origen en la parte más baja de la curva, tal como se muestra en la figura. La ecuación de la cicloide referida a estos ejes es

x=R(2θ+sin(2θ))
y=R(1-cos(2θ))

donde θ es la pendiente de la recta tangente a la cicloide en el punto x

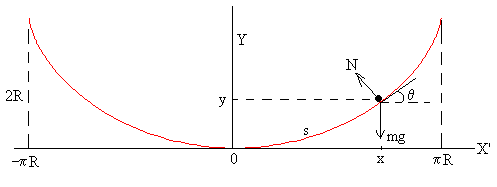
Sobre la partícula actúan dos fuerzas: el peso mg y la reacción de la superficie N. La ecuación del movimiento en la dirección tangencial es

${\displaystyle m\frac{d^{2}s}{d{t}^2}=-mg\sin \theta \frac{d^{2}s}{d{t}^2}+\frac{g}{4R}s=0}$

La partícula describe un Movimiento Armónico Simple(MAS) de frecuencia angular ω, y periodo P

${\displaystyle {\omega }^2=\frac{g}{4R}P=2\pi \sqrt{\frac{4R}{g}}}$

El aspecto más sobresaliente es que el periodo no depende de la amplitud

Si la partícula parte en el instante t=0, del extremo izquierdo (-πR, 2R) con velocidad inicial nula. La ecuación del movimiento es

s=-4R·cos(ωt)

Siendo s la posición de la partícula a lo largo del camino en forma de cicloide. La velocidad de la partícula es

${\displaystyle v=\frac{ds}{dt}=4R\omega ·\sin (\omega t)}$

Balance energético

La partícula se encuentra en inicialmente reposo a una altura 2R, su energía es potencial E=mg·2R.

Cuando pasa por el origen s=0, ωt=π/2, la velocidad de la partícula es v=4Rω. Su energía cinética es E_k=m(4Rω)²/2=2mgR

Comprobamos que la suma de la energía cinética E_k y potencial E_p es constante

${\displaystyle \begin{array}{l}{E}_p=mgy=mgR\left(1-\cos (2\theta )\right)=2mgR{\sin }^2\theta =2mgR\frac{s^2}{16R^2}=2mgR{\cos }^2\left(\omega t\right)\\ E_k=\frac{1}{2}m{v}^2=\frac{1}{2}m·16R^2{\omega }^2{\sin }^2\left(\omega t\right)=2mgR{\sin }^2\left(\omega t\right)\\ E_p+E_k=2mgR\end{array}}$

El principio de conservación de la energía, tiene la misma forma que para un oscilador armónico

${\displaystyle \begin{array}{l}\frac{1}{2}m{v}^2+mgy=E\\ \frac{1}{2}m{\left(\frac{ds}{dt}\right)}^2+mgR\left(1-\cos \left(2\theta \right)\right)=E\\ \frac{1}{2}m{\left(\frac{ds}{dt}\right)}^2+mgR\left(1-{\cos }^2\theta +{\sin }^2\theta \right)=E\\ \frac{1}{2}m{\left(\frac{ds}{dt}\right)}^2+2mgR{\sin }^2\theta =E\\ \frac{1}{2}m{\left(\frac{ds}{dt}\right)}^2+2mgR{\left(\frac{s}{4R}\right)}^2=E\\ \frac{1}{2}m{\left(\frac{ds}{dt}\right)}^2+\frac{mg}{8R}{s}^2=E\end{array}}$

Para un oscilador formado por ua partícula de masa m unida a un muelle elástico de constante k

${\displaystyle \frac{1}{2}m{\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}k{x}^2=E}$

Movimiento a lo largo de la cicloide (con rozamiento)

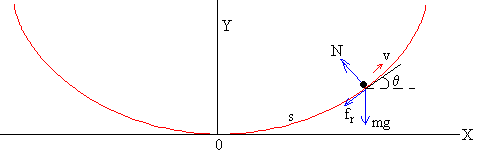
Sobre la partícula actúan tres fuerzas:

• El peso mg

• La reacción de la superficie N en el punto de contacto

• La fuerza de rozamiento, f_r  que se opone al movimiento, de sentido contrario a la velocidad v.

Descomponemos el peso y escribimos las ecuaciones del movimiento en la dirección tangencial y en la dirección normal

ma_t=-mgsinθ-f_r
ma_n=N-mgcosθ

Cuando el cuerpo está deslizando, la fuerza de rozamiento vale

f_r=μN

Teniendo en cuenta las definiciones de la aceleración tangencial a_t y la aceleración normal a_n,

${\displaystyle a_t=\frac{dv}{dt}=\frac{d^{2}s}{d{t}^2}{a}_n=\frac{v^2}{\rho }}$

y eliminando la reacción N de la superficie en el punto de contacto, expresamos las dos ecuaciones del movimiento en una única ecuación diferencial

${\displaystyle \frac{dv}{dt}=-g\sin \theta -\mu g\cos \theta -\mu \frac{v^2}{\rho }}$

La velocidad y la aceleración se expresan en términos del parámetro θ y sus derivadas respecto del tiempo.

${\displaystyle \begin{array}{l}v=\frac{ds}{dt}=4R\cos \theta \frac{d\theta }{dt}\\ \frac{dv}{dt}=-4R\sin \theta {\left(\frac{d\theta }{dt}\right)}^2+4R\cos \theta \frac{d^2\theta }{d{t}^2}\end{array}}$

Se obtiene la ecuación diferencial de segundo orden

${\displaystyle \frac{d^2\theta }{d{t}^2}=-\frac{g}{4R}\left(\mu +\tan \theta \right)+\left(-\mu +\tan \theta \right){\left(\frac{d\theta }{dt}\right)}^2}$

que se resuelve por procedimientos numéricos con las condiciones iniciales t=0, θ=θ₀, dθ/dt=0.

Cuando el cuerpo se mueve hacia la izquierda, la fuerza de rozamiento cambia de sentido, en la ecuación diferencial cambiamos +μ por – μ.

Solución numérica

mu=0.1;  %coeficiente de rozamiento
R=1; %radio
x0=zeros(1,2);
x0(1)=-89*pi/180;  %ángulo de partida
x0(2)=0;    %parte del reposo
f=@(t,x) [x(2);-(9.8/(4*R))*(sign(x(2))*mu+tan(x(1)))+
(-sign(x(2))*mu+tan(x(1)))*x(2)^2]; 
tspan=[0 8];
[t,x]=ode45(f,tspan,x0);

plot(t,4*R*sin(x(:,1)))
ylim([-4,4])
grid on
xlabel('t')
ylabel('s');
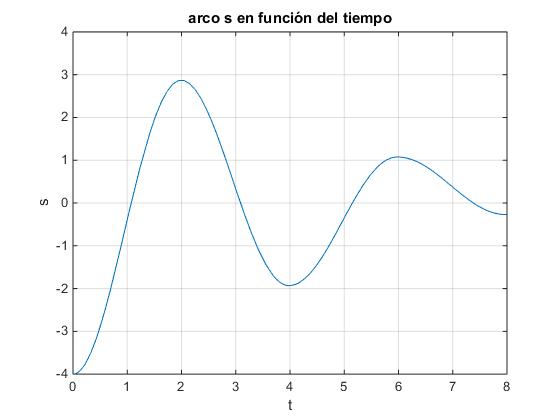
title('arco s en función del tiempo')

Velocidad de la partícula

La ecuación del movimiento se puede integrar para obtener una expresión de la velocidad v en función del parámetro θ.

${\displaystyle \begin{array}{l}\frac{dv}{dt}=-g\sin \theta -\mu g\cos \theta -\mu \frac{v^2}{\rho }\\ v\frac{dv}{ds}=-g\sin \theta -\mu g\cos \theta -\mu \frac{v^2}{4R\cos \theta }\\ \frac{1}{8R\cos \theta }\frac{d{v}^2}{d\theta }=-g\sin \theta -\mu g\cos \theta -\mu \frac{v^2}{4R\cos \theta }\end{array}}$

Llamando $x=\frac{v^2}{2Rg}$ , nos queda la ecuación diferencial

${\displaystyle \frac{dx}{d\theta }+2\mu x=-2\left(\sin \text{(2}\theta )+\mu \cos (2\theta )+\mu \right)}$

La solución de la ecuación diferencial completa es la suma de la solución de la ecuación diferencial homogénea y de la solución particular:

x₁=Asin(2θ)+Bcos(2θ)+C

Introduciendo la solución particular en la ecuación diferencial obtenemos los valores de los coeficientes A, B y C

${\displaystyle A=\frac{-2\mu }{{\mu }^2+1}B=\frac{1-{\mu }^2}{{\mu }^2+1}C=-1}$

Buscamos la solución de la ecuación diferencial homogénea

${\displaystyle \frac{dx}{d\theta }+2\mu x=0\frac{dx}{x}=-2\mu ·d\theta {\displaystyle \int \frac{dx}{x}=-{\displaystyle \int 2\mu ·d\theta }}}$

Integrando ambos miembros obtenemos lnx=-2μθ+lnD, donde lnD es la constante de integración

x₂=D·exp(-2μθ)

La solución completa de la ecuación diferencial es x=x₁+x₂

${\displaystyle \frac{v^2}{2Rg}=D\exp (-2\mu \theta )-\frac{2\mu }{1+{\mu }^2}\sin (2\theta )+\frac{1-{\mu }^2}{1+{\mu }^2}\cos (2\theta )-1}$

La constante D se determina a partir de las condiciones iniciales, en el instante t=0, θ=θ₀, v=0

${\displaystyle \frac{v^2}{2Rg}=\left\{\begin{array}{l}\frac{-2\mu }{1+{\mu }^2}\sin (2\theta )+\frac{1-{\mu }^2}{1+{\mu }^2}\text{cos}(2\theta )-1+\\ \exp \left(2\mu ({\theta }_0-\theta )\right)\left(\frac{2\mu }{1+{\mu }^2}\sin (2{\theta }_0)-\frac{1-{\mu }^2}{1+{\mu }^2}\text{cos}(2{\theta }_0)+1\right)\end{array}\right\}}$

En la figura, se representa v²/(2Rg) en función de la longitud del arco s,  para varios valores del coeficiente de rozamiento μ=0.0, μ=0.25, μ=0.5 y μ=0.75. La posición de partida es θ₀=-89º, s₀≈-4.0.

x0=-89*pi/180;  %ángulo de partida
R=1;
hold on
%sin rozamiento
f=@(x) cos(2*x)-cos(2*x0);
g=@(s) f(asin(s/(4*R)));
fplot(g,[4*R*sin(x0),4*R*sin(-x0)])
%con rozamiento
for mu=0.25:0.25:0.75
    f=@(x) exp(2*mu*(x0-x))*((2*mu*sin(2*x0)-(1-mu^2)*cos(2*x0))
/(1+mu^2)+1)+(-2*mu*sin(2*x)+(1-mu^2)*cos(2*x))/(1+mu^2)-1;
    xf= fzero(f,0) %ángulo de llegada
    g=@(s) f(asin(s/(4*R))); %representa en función del arco
    fplot(g,[4*R*sin(x0),4*R*sin(xf)]);
end
hold off
xlim([-4,4])
grid on
xlabel('s')
ylabel('v^2/(2R·g)')
title('Cuadrado de la velocidad en función del arco s')

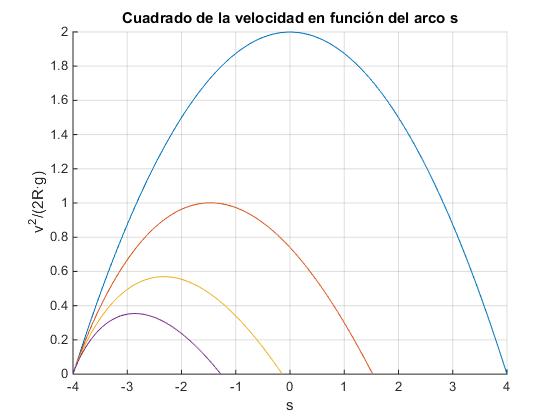
Cuando no hay rozamiento, la partícula vuelve a pararse es s=4.0. Cuando hay rozamiento la posición final es s<4.0.

Sucesivas posiciones de parada

Cuando no hay rozamiento, una partícula que parte de la posición θ₀<0, alcanza su máxima velocidad cuando pasa por el punto más bajo de la trayectoria y se detiene momentáneamente en la posición -θ₀, inicia el camino de vuelta y se detiene en la posición de partida θ₀, y así, sucesivamente.

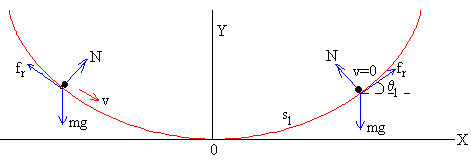
Cuando hay rozamiento, la partícula que parte de la posición θ₀, llega hasta la posición θ₁, se cumple que |θ₀|>|θ₁|. Pueden ocurrir dos casos:

• Que la componente del peso sea mayor que la fuerza de rozamiento (supondremos que μ_s= μ_k= μ)

mgsin|θ₁|≥μ·mgcosθ₁,  o bien que, tan|θ₁|≥μ

La partícula inicia su camino de vuelta, llegando a una posición |θ₂|<|θ₁|

• Que tan|θ₁|<μ

La partícula se para definitivamente

Supongamos que que la partícula prosigue el camino de vuelta hasta la posición θ₂. Si se cumple que tan|θ₂|≥μ, se inicia por segunda vez su camino de ida. En caso contrario, se detiene permanentemente.

Supongamos que la partícula parte de la posición θ_0. Para calcular la posición de parada θ₁ se pone v=0 en la ecuación y se calcula la raíz de la ecuación trascendente.

${\displaystyle \left\{\begin{array}{l}\frac{-2\mu }{1+{\mu }^2}\sin (2\theta )+\frac{1-{\mu }^2}{1+{\mu }^2}\text{cos}(2\theta )-1+\\ \exp \left(2\mu ({\theta }_0-\theta )\right)\left(\frac{2\mu }{1+{\mu }^2}\sin (2{\theta }_0)-\frac{1-{\mu }^2}{1+{\mu }^2}\text{cos}(2{\theta }_0)+1\right)\end{array}\right\}=0}$

o bien,

${\displaystyle \begin{array}{l}\left(\frac{2\mu }{1+{\mu }^2}\sin \left(2{\theta }_0\right)-\frac{1-{\mu }^2}{1+{\mu }^2}\cos \left(2{\theta }_0\right)+1\right)\exp \left(2\mu {\theta }_0\right)=\\ \left(\frac{2\mu }{1+{\mu }^2}\sin \left(2\theta \right)-\frac{1-{\mu }^2}{1+{\mu }^2}\cos \left(2\theta \right)+1\right)\exp \left(2\mu \theta \right)\end{array}}$

Si se cumple que tan|θ₁|≥μ la partícula continúa moviéndose hacia la izquierda, en caso contrario, se detiene permanentemente.

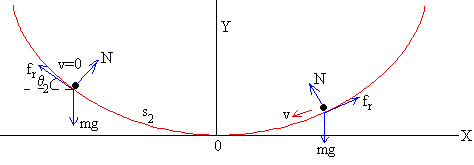
Supongamos que la partícula realiza el camino de vuelta, la fuerza de rozamiento cambia de signo, por lo que en la ecuación anterior cambiamos +μ por – μ. La posición de de parada θ₂, es la raíz de la ecuación trascendente

${\displaystyle \begin{array}{l}\left(-\frac{2\mu }{1+{\mu }^2}\sin \left(2{\theta }_1\right)-\frac{1-{\mu }^2}{1+{\mu }^2}\cos \left(2{\theta }_1\right)+1\right)\exp \left(-2\mu {\theta }_1\right)=\\ \left(-\frac{2\mu }{1+{\mu }^2}\sin \left(2\theta \right)-\frac{1-{\mu }^2}{1+{\mu }^2}\cos \left(2\theta \right)+1\right)\exp \left(-2\mu \theta \right)\end{array}}$

Si se cumple que tan|θ₂|≥μ la partícula continúa moviéndose hacia la derecha, en caso contrario, se detiene permanentemente.

Supongamos que la partícula vuelve a realizar el camino de ida, la fuerza de rozamiento cambia de signo, por lo que en la ecuación anterior cambiamos +μ por – μ. La posición de parada θ₃, es la raíz de la ecuación trascendente

${\displaystyle \begin{array}{l}\left(\frac{2\mu }{1+{\mu }^2}\sin \left(2{\theta }_2\right)-\frac{1-{\mu }^2}{1+{\mu }^2}\cos \left(2{\theta }_2\right)+1\right)\exp \left(2\mu {\theta }_2\right)=\\ \left(\frac{2\mu }{1+{\mu }^2}\sin \left(2\theta \right)-\frac{1-{\mu }^2}{1+{\mu }^2}\cos \left(2\theta \right)+1\right)\exp \left(2\mu \theta \right)\end{array}}$

y así, sucesivamente…

R=1;
x0=-89*pi/180;  %ángulo de partida
mu=0.1;  %coeficiente de rozamiento

while tan(abs(x0))>abs(mu)
    f=@(x)  exp(2*mu*x)*((2*mu*sin(2*x)-(1-mu^2)*cos(2*x))/(1+mu^2)+1);
    g=@(x) f(x)-f(x0);
    x0=fzero(g,0); %ángulo de llegada
    disp(4*R*sin(x0))
    mu=-mu;
end

  2.8765
  -1.9300
   1.0765
  -0.2690

Balance energético

El trabajo de la fuerza de rozamiento es la diferencia entre la energía final y la energía inicial

$$\begin{gathered} {\displaystyle \begin{array}{l}{W}_r=E_f-E_i=\left(\frac{1}{2}m{v}^2+mgy\right)-mg{y}_0= \\ \left(\frac{1}{2}m{v}^2+mgR\left(1-\cos (2\theta )\right)\right)-mgR\left(1-\cos (2{\theta }_0)\right)=\\ \frac{1}{2}m{v}^2+mgR\cos (2{\theta }_0)-mgR\cos (2\theta )\end{array}} \end{gathered}$$

Sustituyendo la larga expresión de v² en esta ecuación se calcula el trabajo de la fuerza de rozamiento cuando la partícula se desplaza desde la posición θ₀ a θ.

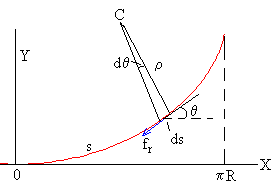
El trabajo de la fuerza de rozamiento se puede calcular también de forma directa

$$\begin{gathered} {\displaystyle d{W}_r=-\mu N·ds=-\mu \left(mg\cos \theta +m\frac{v^2}{R}\right)·ds= \\ -\mu \left(mg\cos \theta +m\frac{v^2}{R}\right)·4R\cos \theta ·d\theta } \end{gathered}$$

Sustituyendo la larga expresión de v² en esta ecuación, e integrando respecto del parámetro θ, obtenemos la expresión del trabajo de la fuerza de rozamiento entre las posiciones θ₀ y θ

Actividades

Se introduce

• El coeficiente de la fuerza de rozamiento μ, en el control titulado Rozamiento.

• El valor del parámetro θ, o ángulo de la recta tangente a la cicloide, en el control titulado Posición inicial. El ángulo tiene que ser estrictamente menor de 90º,

• El valor del parámetro R, o radio del círculo que genera la cicloide se ha fijado en R=1 m.

Se pulsa el botón titulado Nuevo.

• Con rozamiento cero, μ=0

Comprobar que el periodo de una oscilación es

${\displaystyle P=4\pi \sqrt{\frac{R}{g}}=4\pi \sqrt{\frac{1.0}{9.8}}=4.0\text{s}}$

es independiente de la posición inicial de partida

• Con rozamiento μ≠0

Observamos el movimiento de la partícula sobre la superficie cóncava en forma de cicloide, se marcan los puntos de retorno o las posiciones para los cuales la velocidad de la partícula es cero. Cuando en una de estas posiciones se cumple que tan|θ_i|<μ la partícula se para definitivamente. θ_i es el ángulo que forma la recta tangente a la cicloide en el punto de parada.

El programa interactivo, nos describe de forma cualitativa los cambios energéticos que experimenta la partícula. El círculo de mayor radio, representa la energía inicial, que se va perdiendo a causa del trabajo de la fuerza de rozamiento (en color negro). A su vez, la energía de la partícula se transforma de cinética en potencial y viceversa, tal como indican los sectores rojo y azul del círculo de menor radio que representa la energía total de la partícula en cada instante.

En la parte superior, se proporcionan los datos del tiempo t, la posición de la partícula medido por la longitud del arco s a lo largo de la cicloide y la velocidad v de la partícula.

Referencias

Villanueva J. Z. Note on the rough cycloidal slide track. Am. J. Phys. 53 (5) May 1985, pp. 490-491