La energía y el momento angular en coordenadas polares

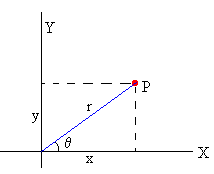
La posición del punto P es

x=r·cosθ
y=r·sinθ

Expresamos la velocidad de la partícula en coordenadas polares

${\displaystyle \overrightarrow{v}=\frac{d\overrightarrow{r}}{dt}=\widehat{r}\frac{dr}{dt}+r\frac{d\widehat{r}}{dt}}$

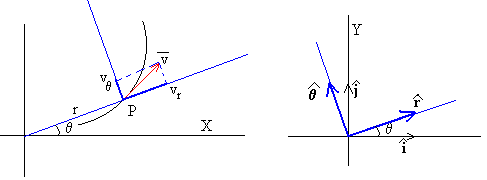
Calculamos las componentes rectangulares de los vectores unitarios $\widehat{r},\widehat{\theta }$

${\displaystyle \begin{array}{l}\widehat{r}=\widehat{i}\cos \theta +\widehat{j}\sin \theta \\ \widehat{\theta }=-\widehat{i}\sin \theta +\widehat{j}\cos \theta \end{array}}$

vemos que

${\displaystyle \frac{d\widehat{r}}{dt}=-\sin \theta \frac{d\theta }{dt}\widehat{i}+\cos \theta \frac{d\theta }{dt}\widehat{j}=\frac{d\theta }{dt}\widehat{\theta }}$

Las componentes del vector velocidad en coordenadas polares son, por tanto

${\displaystyle \overrightarrow{v}=\frac{dr}{dt}\widehat{r}+r\frac{d\theta }{dt}\widehat{\theta }}$

La expresión de la energía en coordenadas polares es

${\displaystyle \begin{array}{l}E=\frac{1}{2}m{v}^2-\frac{GMm}{r}\\ E=\frac{1}{2}m{\left(\frac{dr}{dt}\right)}^2+\frac{1}{2}m{r}^2{\left(\frac{d\theta }{dt}\right)}^2-\frac{GMm}{r}\end{array}}$

Donde -GMm/r es la energía potencial correspondiente a la fuerza conservativa F=GMm/r².

Expresamos el momento angular en coordenadas polares

${\displaystyle \overrightarrow{L}=\overrightarrow{r}\times m\overrightarrow{v}=m\overrightarrow{r}\times \left(\frac{dr}{dt}\widehat{r}+r\frac{d\theta }{dt}\widehat{\theta }\right)=m{r}^2\frac{d\theta }{dt}\widehat{k}}$

Despejamos dθ /dt en la expresión del momento angular y la introducimos en la expresión de la energía. Tenemos dos ecuaciones

${\displaystyle \begin{array}{l}E=\frac{1}{2}m{\left(\frac{dr}{dt}\right)}^2+\frac{L^2}{2m{r}^2}-\frac{GMm}{r}\\ L=m{r}^2\frac{d\theta }{dt}\end{array}}$

Movimiento en la dirección radial

Analizamos la primera ecuación de la energía. Decimos que la partícula se mueve en una región unidimensional r>0 bajo un potencial efectivo, cuyo aspecto se muestra en la figura

${\displaystyle V_{\mathrm{ef}}(r)=\frac{L^2}{2m{r}^2}-\frac{GMm}{r}}$

Se calculan los punto de retorno, la distancia de máximo acercamiento o alejamiento al centro de fuerzas, para una partícula de energía E, cuando la componente radial de la velocidad dr/dt=0

${\displaystyle E=\frac{L^2}{2m{r}^2}-\frac{GMm}{r}}$

Representamos una función de la forma f(r)=a/r²-b/r con a=1 y b=5. Calculamos los puntos de intersección con la recta horizontal e=-2

a=1; 
b=5; 
e=-2; 
f=@(r) a./r.^2-b./r;
fplot(f,[0.2,3],'color','r')
line([0,3],[e,e],'color','k')

%raíces
r1=(-b+sqrt(b^2+4*a*e))/(2*e);
r2=(-b-sqrt(b^2+4*a*e))/(2*e);
line([r1,r1],[0,e], 'lineStyle','--')
line([r2,r2],[0,e],'lineStyle','--')
grid on
xlabel('r')
ylabel('E_{ef}(r)')
title('Energía potencial')

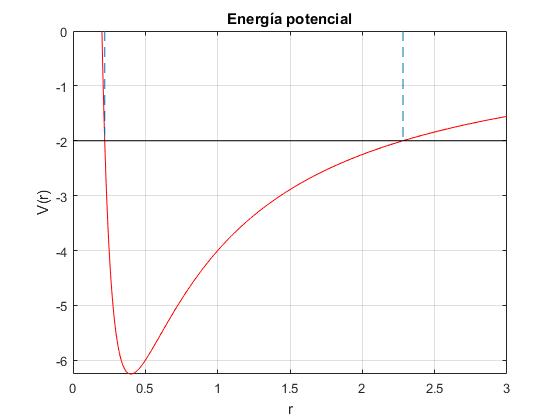
El mínimo se encuentra en la posición r_m=2a/b

>> 2*a/b
ans =    0.4000

La energía E de la partícula puede ser positiva o negativa. El valor de la energía total no puede ser menor que el mínimo de la energía potencial efectiva.

El valor mínimo de obtiene derivando E_p(r) respecto a r e igualando a cero

${\displaystyle -\frac{L^2}{m{r}^3}+\frac{GMm}{r^2}=0r_c=\frac{L^2}{GM{m}^2}}$

El cuerpo describe una trayectoria circular de radio r_c con velocidad v_c. El momento angular L=mr_cv_c.

${\displaystyle v_c^2=\frac{GM}{r_c}}$

La misma expresión, que la que se deduciría a partir de la dinámica del movimiento circular uniforme. La energía vale

${\displaystyle E=-\frac{GMm}{2r_c}}$

Cuando la energía total E es mayor que el mínimo y menor que cero, como vemos en la gráfica, la recta horizontal que señala la energía total corta a curva que describe la energía potencial E_p(r), en dos puntos r₁ y r₂, soluciones de la ecuación de segundo grado

${\displaystyle E=\frac{L^2}{2m{r}^2}-\frac{GMm}{r}}$

Llamando u=1/r

${\displaystyle \begin{array}{l}\frac{L^2}{2m}{u}^2-GMmu-E=0\\ u_{\mathrm{1,2}}=\frac{1\pm \sqrt{1+\frac{2L^{2}E}{G^2{M}^2{m}^3}}}{\frac{L^2}{GM{m}^2}}=\frac{1\pm \epsilon }{d}\\ r_1=\frac{d}{1+\epsilon }{r}_2=\frac{d}{1-\epsilon }\end{array}}$

Donde ε es la excentricidad y d un factor de escala, que obtendremos más abajo al deducir la ecuación de la trayectoria.

• Si la energía E<0 ó ε<1 hay dos raices positivas. La partícula se mueve entre r₁ y r₂
• Si E>0 ó ε>1 solamente hay una raíz positiva, la partícula se mueve entre r₁ e ∞

Fuerza central y conservativa

Utilizamos las propiedades de la fuerza de atracción: central y conservativa, para obtener la ecuación de la trayectoria

En la primera ecuación de la energía sustituímos dr/dt por

${\displaystyle \frac{dr}{dt}=\frac{dr}{d\theta }\frac{d\theta }{dt}=\frac{dr}{d\theta }\frac{L}{m{r}^2}}$

Despejamos dθ/dr para obtener la ecuación de la trayectoria

${\displaystyle \frac{d\theta }{dr}=\frac{\frac{L}{m{r}^2}}{\sqrt{\frac{2}{m}\left(E-\frac{L^2}{2m{r}^2}+\frac{GMm}{r}\right)}}}$

Para integrar se hace el cambio u=1/r

${\displaystyle d\theta =\frac{-du}{\sqrt{-u^2+2\frac{GM{m}^2}{L^2}u+\frac{2mE}{L^2}}}}$

Tenemos una integral del tipo

${\displaystyle \begin{array}{l}\theta =-{\displaystyle \int \frac{du}{\sqrt{-u^2+2bu+c}}}=-{\displaystyle \int \frac{du}{\sqrt{c+b^2-{\left(u-b\right)}^2}}}\\ b=\frac{GM{m}^2}{L^2},c=\frac{2mE}{L^2}\end{array}}$

Hacemos un nuevo cambio de variable

${\displaystyle \begin{array}{l}z=u-b,dz=du\\ \theta =-{\displaystyle \int \frac{-dz}{\sqrt{c+b^2-z^2}}}\\ \theta =-\arcsin \frac{z}{\sqrt{c+b^2}}-C\end{array}}$

Donde C es una constante de integración que determinaremos más adelante. Deshacemos los cambios

${\displaystyle \begin{array}{l}z=\sqrt{c+b^2}\sin \left(-\theta -C\right)\\ \frac{1}{r}-b=-\sqrt{c+b^2}\sin \left(\theta +C\right)\end{array}}$

Tomando C=-π/2, sin(θ-π/2)=-cos(θ).

${\displaystyle \begin{array}{l}\frac{1}{r}-\frac{GM{m}^2}{L^2}=\sqrt{\frac{2mE}{L^2}+\frac{G^2{M}^2{m}^4}{L^4}}\cos \theta \\ \frac{1}{r}-\frac{GM{m}^2}{L^2}=\frac{GM{m}^2}{L^2}\sqrt{\frac{L^4}{G^2{M}^2{m}^4}\frac{2mE}{L^2}+1}\cos \theta \\ \frac{1}{r}-\frac{1}{d}=\frac{\epsilon }{d}\cos \theta ,\{\begin{array}{l}\epsilon =\sqrt{1+\frac{2L^{2}E}{G^2{M}^2{m}^3}}\\ d=\frac{L^2}{GM{m}^2}\end{array}\\ r=\frac{d}{1+\epsilon \cos \theta }\end{array}}$

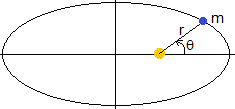
Tomando el valor de la constante C=-π/2, establecemos el origen de ángulos, el ángulo θ=0, cuando la distancia de la partícula al centro de fuerzas es mínima

La ecuación de la trayectoria es una cónica (elipse, parábola o hipérbola) dependiendo del valor de la excentricidad ε.

Las secciones cónicas (elipse, hipérbola y parábola) es el resultado de la intersección de una superficie cónica y un plano

Dibujamos las cónicas de excentricidades (0, 0.3,0.5,0.7,0.8,0.85) elipses, (1) parábola y (1.1,1.3,1.5,2.5) hipérbolas

hold on
for e=[0,0.3,0.5,0.7,0.8,0.85,0.9,1,1.1,1.3,1.5,2.5]
    f=@(x) 1./(1+e*cos(x));
    ang=pi;
    if e>1 %hipérbolas
        ang=acos(-1/e)-pi/180;
    elseif e==1 %parábola
        ang=5*pi/6;
    end
    fplot(@(x) f(x).*cos(x), @(x) f(x).*sin(x) ,[-ang,ang],
 'displayName',num2str(e))
end
legend('-DynamicLegend','Location','northwest')
plot(0,0,'ko','markersize',3,'markeredgecolor','k','markerfacecolor','k')
hold off
axis equal
axis off

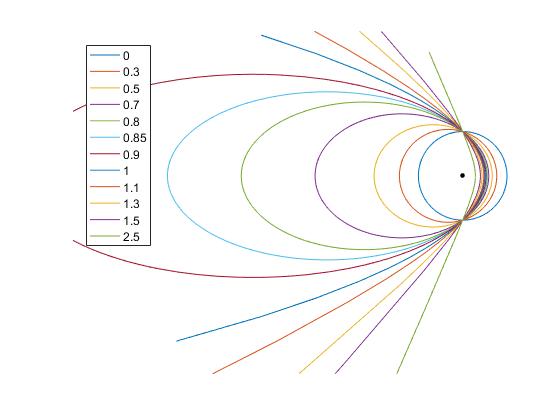
Para ver bien las trayectorias es necesario utilizar los botones Zoom In y Pan de la ventana gráfica

Ecuación del movimiento

En este apartado vamos a obtener la ecuación de la trayectoria aplicando la segunda ley de Newton.

Fuerzas atractivas

En el primer apartado hemos obtenido la expresión del vector velocidad en coordenadas polares. La expresión del vector aceleración es:

${\displaystyle \begin{array}{l}\overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}=\frac{d^{2}r}{d{t}^2}\widehat{r}+\frac{dr}{dt}\frac{d\widehat{r}}{dt}+\left(r\frac{d^2\theta }{d{t}^2}+\frac{dr}{dt}\frac{d\theta }{dt}\right)\widehat{\theta }+r\frac{d\theta }{dt}\frac{d\widehat{\theta }}{dt}=\hfill \\ \frac{d^{2}r}{d{t}^2}\widehat{r}+\frac{dr}{dt}\frac{d\theta }{dt}\widehat{\theta }+\left(r\frac{d^2\theta }{d{t}^2}+\frac{dr}{dt}\frac{d\theta }{dt}\right)\widehat{\theta }-r{\left(\frac{d\theta }{dt}\right)}^2\widehat{r}=\hfill \\ \left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)\widehat{r}+\left(r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}\right)\widehat{\theta }\hfill \end{array}}$

Sobre la partícula de masa m actúa una fuerza atractiva inversamente proporcional al cuadrado de la distancia r al centro de fuerzas. Las ecuaciones del movimiento son

${\displaystyle \begin{array}{l}m\left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)=-G\frac{Mm}{r^2}\\ m\left(r\frac{d^2\theta }{d{t}^2}+2\frac{d\theta }{dt}\frac{dr}{dt}\right)=0\end{array}}$

La segunda ecuación nos indica que el momento angular L (expresado en coordenadas polares es constante)

${\displaystyle \frac{d}{dt}\left(m{r}^2\frac{d\theta }{dt}\right)=0L=m{r}^2\frac{d\theta }{dt}=\text{cte}}$

Teniendo en cuenta la constancia del momento angular L, escribimos la primera ecuación de la forma

${\displaystyle \frac{d^{2}r}{d{t}^2}-\frac{L^2}{m^2{r}^3}=-G\frac{M}{r^2}}$

Para calcular la ecuación de la trayectoria r=r(θ), eliminamos el tiempo t del siguiente modo

${\displaystyle \begin{array}{l}\frac{dr}{dt}=\frac{dr}{d\theta }\frac{d\theta }{dt}=\frac{L}{m{r}^2}\frac{dr}{d\theta }\\ \frac{d^{2}r}{d{t}^2}=\frac{d}{dt}\left(\frac{L}{m{r}^2}\frac{dr}{d\theta }\right)=\frac{d}{d\theta }\left(\frac{L}{m{r}^2}\frac{dr}{d\theta }\right)\frac{d\theta }{dt}=\frac{L}{m{r}^2}\frac{d}{d\theta }\left(\frac{L}{m{r}^2}\frac{dr}{d\theta }\right)\\ \frac{d^{2}r}{d{t}^2}=\frac{L^2}{m^2{r}^4}\left(\frac{d^{2}r}{d{\theta }^2}-\frac{2}{r}{\left(\frac{dr}{d\theta }\right)}^2\right)\end{array}}$

Obtenemos una ecuación en términos de r y de sus derivadas respecto del ángulo θ

${\displaystyle \frac{d^{2}r}{d{\theta }^2}-\frac{2}{r}{\left(\frac{dr}{d\theta }\right)}^2-r=-\frac{GM{m}^2}{L^2}{r}^2}$

Hacemos el cambio de variable u=1/r

${\displaystyle \begin{array}{l}\frac{dr}{d\theta }=-\frac{1}{u^2}\frac{du}{d\theta }\\ \frac{d^{2}r}{d\theta }=\frac{2}{u^3}{\left(\frac{du}{d\theta }\right)}^2-\frac{1}{u^2}\frac{d^{2}u}{d{\theta }^2}\end{array}}$

la ecuación del movimiento se convierte en

${\displaystyle \frac{d^{2}u}{d{\theta }^2}+u=\frac{GM{m}^2}{L^2}}$

La solución de la ecuación diferencial es

${\displaystyle u=A\sin \theta +B\cos \theta +\frac{GM{m}^2}{L^2}}$

En forma equivalente, escribiendo

${\displaystyle \begin{array}{l}A\frac{L^2}{GM{m}^2}=\epsilon \sin {\theta }_{0}B\frac{L^2}{GM{m}^2}=\epsilon \cos {\theta }_0\\ u=\frac{GM{m}^2}{L^2}\left(\epsilon \cos (\theta -{\theta }_0)+1\right)\end{array}}$

Calculamos la constante ε a partir de la conservación de la energía.

${\displaystyle \begin{array}{l}E=\frac{1}{2}m\left\{{\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2\right\}-\frac{GMm}{r}\\ E=\frac{1}{2}\frac{L^2}{m{r}^4}\left\{{\left(\frac{dr}{d\theta }\right)}^2+r^2\right\}-\frac{GMm}{r}\\ E=\frac{1}{2}\frac{L^2}{m}{u}^4\left\{\frac{1}{u^4}{\left(\frac{du}{d\theta }\right)}^2+\frac{1}{u^2}\right\}-GMmu\\ E=\frac{1}{2}\frac{L^2}{m}\left\{{\left(\frac{du}{d\theta }\right)}^2+u^2\right\}-GMmu\end{array}}$

Introduciendo la expresión de u y su derivada du/dθ, obtenemos

${\displaystyle \epsilon =\sqrt{1+\frac{2L^2}{G^2{M}^2{m}^3}E}}$

La ecuación de la trayectoria es r=1/u

${\displaystyle \frac{1}{r}=\frac{GM{m}^2}{L^2}\left(\epsilon \cos (\theta -{\theta }_0)+1\right)}$

Ejemplo

Un planeta parte de la posición (r=2/3, θ=0). Las componentes de la velocidad son dr/dt=0 y dθ/dt=9/4 en un sistema de unidades en el que GM=1

El momento angular es

${\displaystyle \begin{array}{l}L=m{r}^2\frac{d\theta }{dt}\\ L=m{\left(\frac{2}{3}\right)}^2\frac{9}{4}=m\end{array}}$

La ecuación de la trayectoria

${\displaystyle \begin{array}{l}\frac{1}{r}=A\sin \theta +B\cos \theta +\frac{GM{m}^2}{L^2}\\ \frac{1}{r}=A\sin \theta +B\cos \theta +1\end{array}}$

Los coeficientes A y B se determinan a partir de las condiciones iniciales: distancia al origen y velocidad en la dirección radial para θ=0

${\displaystyle \begin{array}{l}\frac{3}{2}=B+1\\ B=\frac{1}{2}\\ -\frac{1}{r}\frac{dr}{d\theta }=A\cos \theta -B\sin \theta \\ A=0\end{array}}$

La ecuación de la trayectoria

${\displaystyle \frac{1}{r}=\frac{1}{2}\cos \theta +1}$

 r=@(x) 1./(cos(x)/2+1);
 hold on
 fplot(@(x) r(x).*cos(x), @(x) r(x).*sin(x), [0,2*pi])
 plot(0,0,'ro','markersize',4,'markerfacecolor','r') %Sol
 hold off
 grid on
 xlabel('x')
 ylabel('y')
 title('Trayectoria')

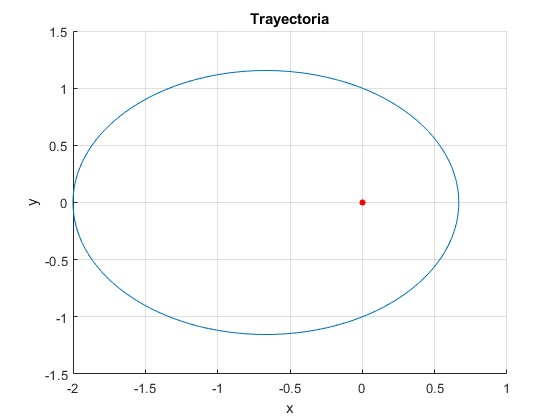
El punto de color rojo en el origen es el centro defuerzas, el Sol

Precesión

La trayectoria que siguen los planetas es elíptica, salvo la de Mercurio que tiene un movimiento de precesión que simulamos a continuación

A la ecuación diferencial del movimiento, se la añade una corrección relativista, inversamente proporcional al cuadrado de la distancia r al centro de fuerzas

${\displaystyle \frac{d^{2}u}{d{\theta }^2}+u=\frac{GM{m}^2}{L^2}+\frac{3GM}{c^2}{u}^2,u=\frac{1}{r}}$

Donde c es la velocidad de la luz

Resolvemos esta ecuación diferencial por procedimientos numéricos, tomando c=8, en el sistema de unidades elegido

function mercurio
    c=8;
    f=@(t,x) [x(2);-x(1)+1+3*x(1)^2/c^2]; 
    opts=odeset('events',@opcion1_ode45);
    [phi,u,pe,ue]=ode45(f,[0,10*pi],[3/2, 0],opts);
    hold on
    plot(cos(phi)./u(:,1), sin(phi)./u(:,1))
    plot(cos(pe)./ue(:,1),sin(pe)./ue(:,1),'o','markersize',3,
'markerfacecolor','r')
    disp(pe)
    plot(0,0,'ro','markersize',4,'markerfacecolor','r') %Sol
    hold off
    grid on
    axis equal
    xlabel('x')
    ylabel('y')
    title('Órbita de Mercurio')

    function [value,isterminal,direction]=opcion1_ode45(~,x)
       value=x(2); 
       isterminal=0;
       direction=1; 
    end
end

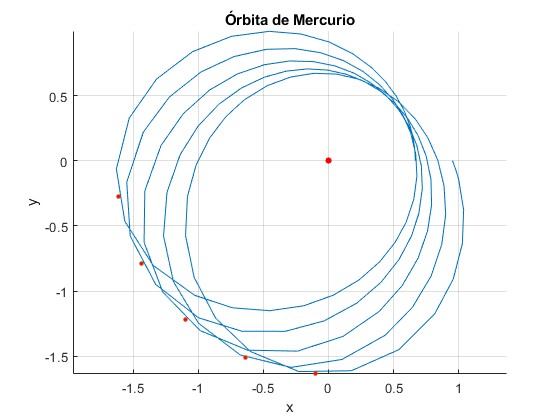
Mediante puntos de color rojo, señalamos las sucesivas posiciones del afelio, dr/dt=0

    3.3092
    9.9277
   16.5460
   23.1642
   29.7822

Su avance es δθ=θ_i+1-θ_i-2π. Por ejemplo,

9.9277-3.3092-2π=0.3353

16.5460-9.9277-2π=0.3351

23.1642-16.5460-2π=0.3350

Fuerzas repulsivas

Sobre la partícula actúa una fuerza repulsiva inversamente proporcional al cuadrado de la distancia r al centro de fuerzas. Por ejemplo, un núcleo fijo de carga Q que repele a una partícula alfa de masa m y carga q. Las ecuaciones del movimiento son

${\displaystyle \begin{array}{l}m\left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)=\frac{k}{r^2}k=\frac{Qq}{4\pi {\epsilon }_0}\hfill \\ m\left(r\frac{d^2\theta }{d{t}^2}+2\frac{d\theta }{dt}\frac{dr}{dt}\right)=0\hfill \end{array}}$

Siguiendo los mismos pasos que para la fuerza atractiva, la solución es

${\displaystyle u=A\sin \theta +B\cos \theta -\frac{km}{L^2}}$

De forma equivalente

${\displaystyle u=\frac{km}{L^2}\left(\epsilon \cos (\theta -{\theta }_0)-1\right)}$

Calculamos la constante ε a partir de la conservación de la energía.

${\displaystyle \begin{array}{l}E=\frac{1}{2}m\left\{{\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2\right\}+\frac{k}{r}\\ E=\frac{1}{2}\frac{L^2}{m}\left\{{\left(\frac{du}{d\theta }\right)}^2+u^2\right\}+ku\end{array}}$

Introduciendo la expresión de u y su derivada du/dθ, obtenemos

${\displaystyle \epsilon =\sqrt{1+\frac{2L^2}{k^{2}m}E}}$

La ecuación de la trayectoria es r=1/u

${\displaystyle \frac{1}{r}=\frac{km}{L^2}\left(\epsilon \cos (\theta -{\theta }_0)-1\right)}$

Trayectorias circulares

La energía potencial efectiva para una partícula que se mueve bajo la acción de una fuerza atractiva inversamente proporcional al cuadrado de la distancia, F=-GMM/r² es

${\displaystyle V_{\mathrm{ef}}(r)=\frac{L^2}{2m{r}^2}-\frac{GMm}{r}}$

El mínimo de esta función corresponde a trayectorias circulares estables de radio r_c=L²/(GMm²)

Supongamos una fuerza cuyo potencial es V(r)=krⁿ. Si la fuerza es atractiva k<0, repulsiva k>0. La energía potencial efectiva es

${\displaystyle V_{ef}(r)=\frac{L^2}{2m{r}^2}+k{r}^n}$

El extremo (máximo o mínimo) de esta función es

${\displaystyle \begin{array}{l}\frac{d{V}_{eff}(r)}{dr}=-\frac{L^2}{m{r}^3}+nk{r}^{n-1}=0\\ r_c^{n+2}=\frac{L^2}{mnk}\end{array}}$

para que r_c sea positivo, k>0 (repulsiva) y n>0, o k<0 (atractiva) y n<0

Calculamos la derivada segunda

${\displaystyle \frac{d^2{V}_{eff}(r)}{d{r}^2}=3\frac{L^2}{m{r}^4}+n\left(n-1\right)k{r}^{n-2}=\frac{1}{r^4}\left(3\frac{L^2}{m}+n\left(n-1\right)k{r}^{n+2}\right)}$

Para que la trayectoria circular de radio r_c sea estable

${\displaystyle \begin{array}{l}{\frac{d^2{V}_{eff}(r)}{d{r}^2}|}_{r=r_c}=\frac{1}{r_0^4}\frac{L^2}{m}\left(3+n-1\right)>0\\ n>-2\end{array}}$

• Fuerza repulsiva, k>0 y n>0
• Fuerza atractiva, k<0 y -2<n<0

Para una fuerza atractiva k<0, con n=-1, tenemos trayectorias circulares estables

Referencias

W. G. Rees. Physics by Example. 200 problems and solutions. Cambridge University Press, (1994), Problem 41, pp.90-92

Hollis Williams. An elementary approach to simulating the perihelion of Mercury. Eur. J. Phys. 44 (2023) 065602