Movimiento relativo en el Sistema de Referencia Local
Sistema de referencia local
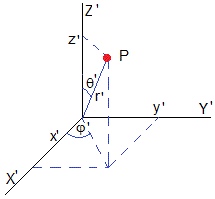
Supongamos inicialmente que la Tierra no gira. Situamos el Sistema de Referencia Inercial S' con origen en el centro de la Tierra, con el eje Z' en la dirección del eje de rotación. La posición de un punto P es
Si el punto P está en la superficie de la Tierra de radio r'=R (radio de la Tierra)
El Sistema de Referencia Local S tiene su origen en el punto P, y los ejes orientados en la dirección radial, en la dirección Este (tangente al paralelo del lugar) y la dirección Sur (tangente al meridiano del lugar). Véase la figura debajo del código, más abajo.
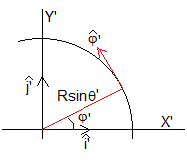
Para determinar las direcciones de estos ejes, relacionando los vectores unitarios con del siguiente modo:
El vector unitario tiene la misma dirección y sentido que el vector , por tanto
El vector unitario , es tangente al paralelo de radio Rsinθ', tal como se ve en la figura.
El vector unitario es el producto vectorial de . Utilizamos la función MATLAB
cross para realizar el producto vectorial
Su módulo es la unidad
%x=theta, y=phi >> syms x y; >> r=[sin(x)*cos(y),sin(x)*sin(y),cos(x)]; >> phi=[-sin(y),cos(y),0]; >> simplify(cross(phi,r)) ans =[ cos(x)*cos(y), cos(x)*sin(y), -sin(x)]
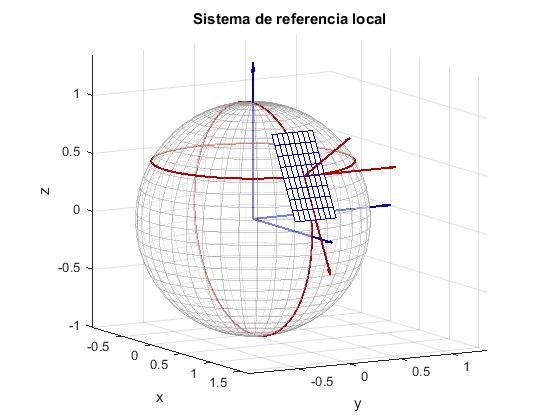
Utilizamos MATLAB para dibujar el Sistema de Referencia Inercial S' con origen en el centro de la Tierra, y los ejes X', Y' y Z' en color azul. El ángulo θ=60° o bien, la latitud es λ=30°. La longitud se ha establecido en φ=0. Se muestra el plano local, tangente a la superficie esférica en el punto P y el Sistema de Referencia Local S cuyo origen está en el punto P, en color rojo los ejes señalados por las direcciones de los vectores unitarios . Dirección radial, tangente al paralelo, hacia el Este y tangente al meridiano del lugar, hacia el Sur
%esfera
R=1;
phi=linspace(0,pi,30);
theta=linspace(0,2*pi,40);
[phi,theta]=meshgrid(phi,theta);
x=R*sin(phi).*cos(theta);
y=R*sin(phi).*sin(theta);
z=R*cos(phi);
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0.6,0.6,0.6],'EdgeAlpha',0.5,'FaceAlpha',0.5)
axis equal
%paralelo
theta=pi/3;
phi=0:0.1:2*pi;
x=sin(theta)*cos(phi);
y=sin(theta)*sin(phi);
z=cos(theta)*ones(1,length(x));
h1=line(x,y,z);
set(h1,'Color',[.7,0,0],'LineWidth',1.5)
%meridiano
phi=0;
theta=-pi:0.1:pi;
x=sin(theta)*cos(phi);
y=sin(theta)*sin(phi);
z=cos(theta);
h1=line(x,y,z);
set(h1,'Color',[.7,0,0],'LineWidth',1.5)
%plano tangente
phi=0;
theta=pi/3;
x0=sin(theta)*cos(phi);
y0=sin(theta)*sin(phi);
z0=cos(theta);
[x,y]=meshgrid(-0.2+x0:0.05:0.2+x0,-0.2+y0:0.05:0.2+y0);
z=(1-x*x0-y*y0)/z0;
hold on
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0,0,0.8])
%Sistema de referencia local S
h1=quiver3(x0,y0,z0,sin(theta)*cos(phi),sin(theta)*sin(phi), cos(theta));
set(h1,'Color',[.7,0,0],'LineWidth',1.5)
h1=quiver3(x0,y0,z0,cos(theta)*cos(phi),cos(theta)*sin(phi), -sin(theta));
set(h1,'Color',[.7,0,0],'LineWidth',1.5)
h1=quiver3(x0,y0,z0,-sin(phi),cos(phi),0);
set(h1,'Color',[.7,0,0],'LineWidth',1.5)
%sistema de referencia S'inercial
h1=quiver3(0,0,0, 1.5,0,0);
set(h1,'Color',[0,0,0.7],'LineWidth',1.5)
h1=quiver3(0,0,0, 0,1.5,0);
set(h1,'Color',[0,0,0.7],'LineWidth',1.5)
h1=quiver3(0,0,0, 0,0,1.5);
set(h1,'Color',[0,0,0.7],'LineWidth',1.5)
axis equal
view(60,10)
hold off
xlabel('x'); ylabel('y'); zlabel('z')
title('Sistema de referencia local')
Sea un punto Q cercano a la superficie de la Tierra, su posición relativa al Sistema de Referencia Local S es
El vector posición de Q relativo al Sistema de Referencia Inercial S' en el centro de la Tierra es
Relacionamos las componentes (x,y,z) del punto Q en el Sistema de Referencia Local S con las componentes de Q (x',y',z') en el Sistema de referencia S' con origen en el centro de la Tierra.
Una vez definido el Sistema de Referencia Local S, denominaremos a sus ejes X (hacia el Sur), Y (hacia el Este) y Z (vertical) y a los vectores unitarios a lo largo de los ejes . De modo, que el vector posición del punto Q se escribe ahora
Posición y velocidad de la partícula
Como la Tierra gira alrededor del eje Z' con velocidad angular constante Ω, entonces, φ'=Ω·t. Denominando α=θ'. La relación entre las componentes (x,y,z) del punto Q en el Sistema de Referencia Local S con las componentes de Q (x',y',z') en el Sistema de Referencia Inercial S' con origen en el centro de la Tierra es
Derivando con respecto del tiempo obtenemos las componentes de la velocidad de la partícula en el Sistema de Referencia Inercial S' conocidas las componentes de la velocidad de la partícula en el Sistema de Referencia Local S
Calculamos la energía cinética T de la partícula en el Sistema de Referencia Inercial S'
Para obtener esta larga expresión, se ha utilizado Math Symbolic. En primer lugar, se emplean las variables: W=Ω, vx=dx/dt, vy=dy/dt, vz=dz/dt, x, y, Rz=R+z para nombrar símbolos matemáticos.
syms a W vx vy vz x y Rz; vXp=vx*cos(a)*cos(W)-vy*sin(W)+vz*sin(a)*cos(W)-W*(x*cos(a)*sin(W)+ y*cos(W)+Rz*sin(a)*sin(W)); vYp=vx*cos(a)*sin(W)+vy*cos(W)+vz*sin(a)*sin(W)+W*(x*cos(a)*cos(W)- y*sin(W)+Rz*sin(a)*cos(W)); vZp=-vx*sin(a)+vz*cos(a); vp2=expand(vXp^2+vYp^2+vZp^2); vp2=simplify(vp2) collect(vp2, W)
La respuesta
>> latex(ans)
ans =
\left( - {\mathrm{Rz}}^2\, {\cos\!\left(a\right)}^2 + {\mathrm{Rz}}^2 +
\sin\!\left(2\, a\right)\, \mathrm{Rz}\, x + x^2\, {\cos\!\left(a\right)}^2 +
y^2\right)\, W^2 + \left(2\, \mathrm{vy}\, x\, \cos\!\left(a\right) - 2\,
\mathrm{vx}\, y\, \cos\!\left(a\right) - 2\, \mathrm{vz}\, y\,
\sin\!\left(a\right) + 2\, \mathrm{Rz}\, \mathrm{vy}\,
\sin\!\left(a\right)\right)\, W + \left({\mathrm{vx}}^2 + {\mathrm{vy}}^2 +
{\mathrm{vz}}^2\right)
Determinaremos la energía potencial V(x,y,z) en cada una de las situaciones que vamos a estudiar.
Ecuaciones del movimiento
La lagrangiana L=T-V de la partícula en el Sistema de Referencia Inercial S' es
Las ecuaciones del movimiento se escriben
Caída de una partícula
El primer ejemplo que vamos a estudiar es una partícula que se deja caer desde una altura h. La energía potencial V(x,y,z)=mg0z
Como el radio de la Tierra R es muy grande comparado con x o z, las ecuaciones del movimiento se pueden aproximar a las siguientes
Resolvemos por dos métodos, este sistema de ecuaciones con las siguientes condiciones iniciales
Denominamos g=g0-Ω2Rsin2α y k=Ω2Rsin(2α)/2
Resolvemos el sistema de tres ecuaciones diferenciales por el procedimiento
R=6.378e6; %radio de la tierra en m
W=2*pi/(24*3600); %velocidad angular de rotación de la Tierra
alfa=pi/6; %posición
k=W^2*R*sin(2*alfa)/2;
g=9.81-W^2*R*sin(alfa)^2;
h=1000; %altura de caída
%x es x(1), dx/dt es x(2), y es x(3), dy/dt es x(4), z es x(5) y dz/dt es x(6)
f=@(t,x)[x(2); 2*W*x(4)*cos(alfa)+k;x(4); -2*W*(x(2)*cos(alfa)+x(6)*sin(alfa));
x(6); 2*W*x(4)*sin(alfa)-g];
[t,x]=ode45(f,[0,sqrt(2*h/g)],[0,0,0,0,h,0]);
plot3(x(:,1),x(:,3),x(:,5))
grid on
xlabel('X: N-S')
ylabel('y: O-E')
zlabel('z, radial')
title('Caída de un cuerpo sobre la superficie de la tierra')
view(107,12)
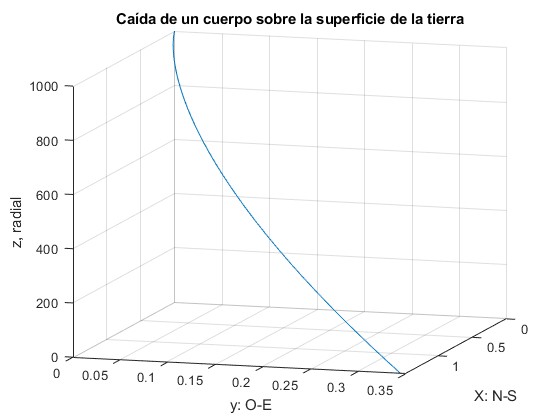
>> x(end,1) ans = 1.4903 >> x(end,3) ans = 0.3454
Los números que aparecen en este cuadro se interpretan del siguiente modo (véase la gráfica): cuando la partícula llega al suelo z=0, la desviación hacia el Sur es x=1.4903, en el código
Aproximaciones sucesivas
Integramos la primera y tercera ecuación diferencial, (variables separadas) con las condiciones iniciales especificadas.
Se sustituye dx/dt y dz/dt en la segunda ecuación diferencial
La solución de esta ecuación diferencial es la suma de una particular yp=At y de la homogénea. Introducimos en la ecuación diferencial para determinar A
La ecuación diferencial homogénea es similar a la de un movimiento armónico simple, xh=C=cos(2Ωt)+Dsin(2Ωt). La solución completa es. La solución completa es
Donde C y D se determinan a partir de las condiciones iniciales: en el instante t=0, y=0, y dy/dt=0.
Conocido y, integramos las ecuaciones de primer orden en x con las condiciones iniciales: en el instante t=0, x=0.
Conocido y, integramos las ecuaciones de primer orden en z con las condiciones iniciales: en el instante t=0, z=h.
R=6.378e6; %radio de la tierra en m
W=2*pi/(24*3600); %velocidad angular de rotación de la Tierra
alfa=pi/6; %posición
k=W^2*R*sin(2*alfa)/2;
g=9.81-W^2*R*sin(alfa)^2;
h=1000; %altura de caída
y=@(t) (g*sin(alfa)-k*cos(alfa))*(t-sin(2*W*t)/(2*W))/(2*W);
x=@(t) (g*sin(alfa)*cos(alfa)-k*cos(alfa)^2+k)*t.^2/2-(g*sin(alfa)-k*cos(alfa))
*cos(alfa)*(1-cos(2*W*t))/(4*W^2);
z=@(t) h-(g*cos(alfa)+k*sin(alfa))*cos(alfa)*t.^2/2-(g*sin(alfa)-k*cos(alfa))
*sin(alfa)*(1-cos(2*W*t))/(4*W^2);
fplot3(x,y,z,[0,sqrt(2*h/g)])
grid on
xlabel('X: N-S')
ylabel('y: O-E')
zlabel('z, radial')
title('Caída de un cuerpo sobre la superficie de la tierra')
view(107,12)
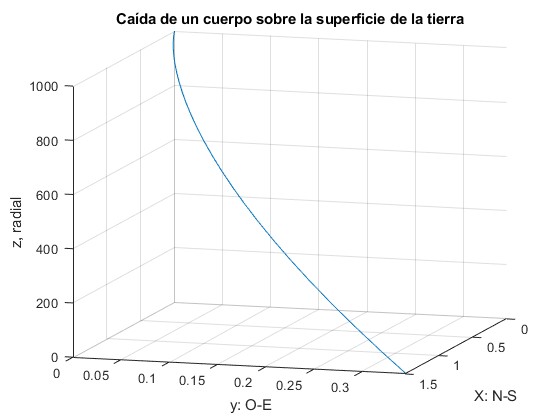
>> x(sqrt(2*h/g)) ans = 1.4903 >> y(sqrt(2*h/g)) ans = 0.3454
Los números que aparecen en este cuadro se interpretan del siguiente modo (véase la gráfica): cuando la partícula llega al suelo z=0, la desviación hacia el Sur es x=1.4903, en el código y la desviación hacia el Este es y=0.3454. El mismo resultado que resolviendo por procedimientos numéricos el sistema de tres ecuaciones diferenciales
Efecto de la fuerza de Coriolis
La velocidad angular de rotación de la Tierra Ω=2π/(24·60·60)=7.2722·10-5 rad/s es pequeña, por lo que despreciamos en el sistema de tres ecuaciones diferenciales los dos términos en Ω2. El sistema de tres ecuaciones diferenciales que tenemos que resolver por el procedimiento de aproximaciones sucesivas es el siguiente
Integramos
Con las condiciones iniciales especificadas, las tres constantes valen
El sistema de tres ecuaciones diferenciales es
Introducimos dx/dt y dz/dt en la segunda ecuación diferencial
La solución de esta ecuación diferencial se compone de la solución particular yp=Ct
y la solución de la ecuación diferencial homogénea yh=Acos(2Ωt)+Bsin(2Ωt). La solución completa es
Donde A y B se determinan a partir de las condiciones iniciales
Insertamos la y en las ecuaciones diferenciales
Integramos con la condición inicial x(0)=0
Hacemos lo mismo para z
La constante c se determina a partir de la condición inicial z(0)=h
La solución es
Aproximaciones, como Ωt<<1
>> syms t w; >> taylor(sin(2*w*t)) ans =(4*t^5*w^5)/15 - (4*t^3*w^3)/3 + 2*t*w >> taylor(cos(2*w*t)) ans =(2*t^4*w^4)/3 - 2*t^2*w^2 + 1
Despreciamos términos proporcionales a Ω2
R=6.378e6; %radio de la tierra en m
W=2*pi/(24*3600); %velocidad angular de rotación de la Tierra
alfa=pi/6; %posición
g=9.81;
h=1000; %altura de caída
x=@(t) g*W^2*t.^4*sin(alfa)*cos(alfa)/6;
y=@(t) g*W*t.^3*sin(alfa)/3;
z=@(t) h-g*t.^2/2+g*W^2*t.^4*sin(alfa)^2/6;
fplot3(x,y,z,[0,sqrt(2*h/g)])
grid on
xlabel('X: N-S')
ylabel('y: O-E')
zlabel('z, radial')
title('Caída de un cuerpo sobre la superficie de la tierra')
view(107,12)
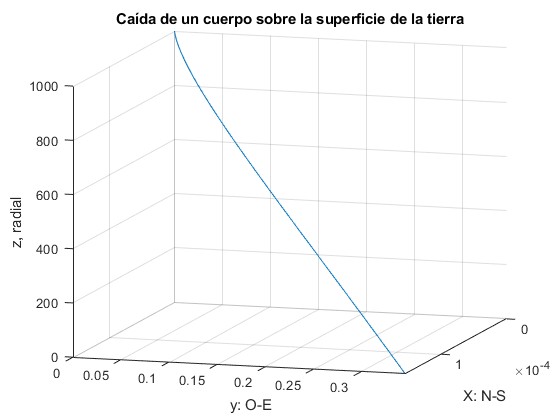
>> x(sqrt(2*h/g)) ans = 1.5562e-04 >> y(sqrt(2*h/g)) ans = 0.3461
La desviación hacia el este 0.3461 m coincide, aproximadamente, con el cálculo anterior
Se lanza verticalmente una partícula
Volvemos a resolver el sistema de tres ecuaciones diferenciales por el procedimiento de aproximaciones sucesivas con condiciones iniciales diferentes
Integramos
Con las condiciones iniciales especificadas, las tres constantes valen
El sistema de tres ecuaciones diferenciales es
Introducimos dx/dt y dz/dt en la segunda ecuación diferencial
La solución de esta ecuación diferencial se compone de la solución particular yp=Ct+D
y la solución de la ecuación diferencial homogénea yh=Acos(2Ωt)+Bsin(2Ωt). La solución completa es
Donde A y B se determinan a partir de las condiciones iniciales
Insertamos la y en las ecuaciones diferenciales
Integramos con la condición inicial x(0)=0
Hacemos lo mismo para z sabiendo que z(0)=0
La solución es
Aproximaciones, como Ωt<<1
El resultado es
Simplificando
Despreciamos términos proporcionales a Ω2
R=6.378e6; %radio de la tierra en m
W=2*pi/(24*3600); %velocidad angular de rotación de la Tierra
alfa=pi/6; %posición
g=9.81;
h=1000; %altura máxima
v0=sqrt(2*g*h); %velocidad inicial
x=@(t) W^2*(g*t/2-2*v0).*t.^3*sin(alfa)*cos(alfa)/3;
y=@(t) W*(g*t/3-v0).*t.^2*sin(alfa);
z=@(t) v0*t+W^2*(g*t/6-2*v0/3).*t.^3*sin(alfa)^2-g*t.^2/2;
fplot3(x,y,z,[0,2*v0/g])
grid on
xlabel('X: N-S')
ylabel('y: O-E')
zlabel('z, radial')
title('Se lanza un cuerpo verticalmente')
view(107,12)
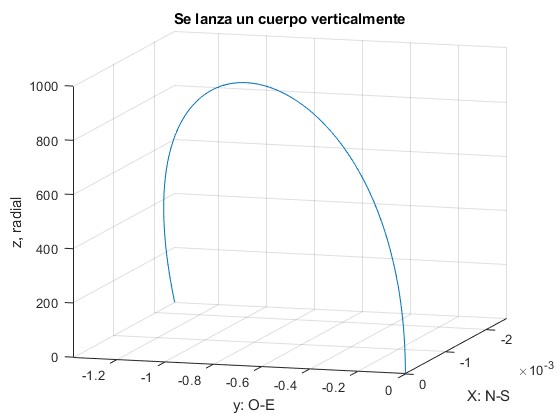
>> T=2*v0/g T = 28.5569 >> x(T) ans = -0.0025 >> y(T) ans = -1.3845 >> y=(g*T/3-v0)*W*T^2*sin(alfa) y = -1.3845
La desviación hacia el oeste es 1.3845 m
Tiro parabólico
Volvemos a resolver el sistema de tres ecuaciones diferenciales por el procedimiento de aproximaciones sucesivas con condiciones iniciales diferentes
Integramos
Con las condiciones iniciales especificadas, las tres constantes valen
El sistema de tres ecuaciones diferenciales es
Introducimos dx/dt y dz/dt en la segunda ecuación diferencial
La solución de esta ecuación diferencial se compone de la solución particular yp=Ct+D
y la solución de la ecuación diferencial homogénea yh=Acos(2Ωt)+Bsin(2Ωt). La solución completa es
Donde A y B se determinan a partir de las condiciones iniciales
Insertamos la y en las ecuaciones diferenciales
Integramos con la condición inicial x(0)=0
Hacemos lo mismo para z, sabiendo que z(0)=0
La solución es
Aproximaciones, como Ωt<<1
El resultado es
Simplificando
Despreciamos términos proporcionales a Ω2
Tiro parabólico Norte - Sur
La velocidad inicial de disparo es v0=140 m/s, el ángulo de tiro θ=π/3 (60°). v0x=v0cosθ, v0y=0, v0z=v0sinθ
Utilizamos la función
R=6.378e6; %radio de la tierra en m
W=2*pi/(24*3600); %velocidad angular de rotación de la Tierra
alfa=pi/6; %posición
a_tiro=pi/3; %ángulo de tiro
v0x=140*cos(a_tiro);
v0z=140*sin(a_tiro);
v0y=0;
g=9.81;
x=@(t) v0x*t+W*t.^2*v0y*cos(alfa);
y=@(t) W*t.^3*g*sin(alfa)/3-(v0x*cos(alfa)+v0z*sin(alfa))*W*t.^2+v0y*t;
z=@(t) v0z*t-g*t.^2/2+W*t.^2*v0y*sin(alfa);
T=fzero(z,2*v0/g);
fplot3(x,y,z,[0,T])
xlabel('X: N-S')
ylabel('y: O-E')
zlabel('z, radial')
title('Tiro parabólico N-->S')
view(107,12)
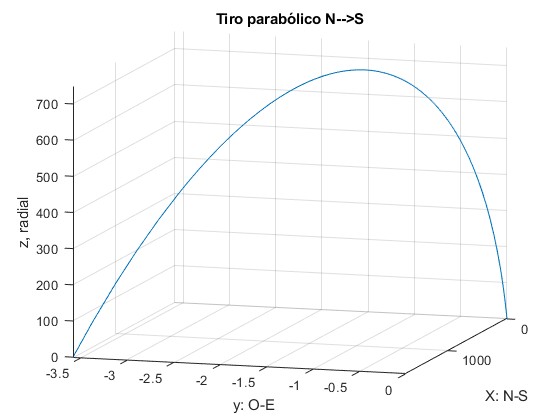
>> T T = 24.7184 >> x(T) ans = 1.7303e+03 >> y(T) ans = -3.5915
El alcance es 1730 m y la desviación hacia el oeste y=3.5915 m
Tiro parabólico Oeste-Este
La velocidad inicial de disparo es v0=140 m/s, el ángulo de tiro θ=π/3 (60°). v0x=0, v0y=v0cosθ, v0z=v0sinθ
R=6.378e6; %radio de la tierra en m
W=2*pi/(24*3600); %velocidad angular de rotación de la Tierra
alfa=pi/6; %posición
a_tiro=pi/3; %ángulo de tiro
v0y=140*cos(a_tiro);
v0z=140*sin(a_tiro);
v0x=0;
g=9.81;
x=@(t) v0x*t+W*t.^2*v0y*cos(alfa);
y=@(t) W*t.^3*g*sin(alfa)/3-(v0x*cos(alfa)+v0z*sin(alfa))*W*t.^2+v0y*t;
z=@(t) v0z*t-g*t.^2/2+W*t.^2*v0y*sin(alfa);
T=fzero(z,2*v0/g);
fplot3(x,y,z,[0,T])
xlabel('X: N-S')
ylabel('y: O-E')
zlabel('z, radial')
title('Tiro parabólico, O-->E')
view(107,12)
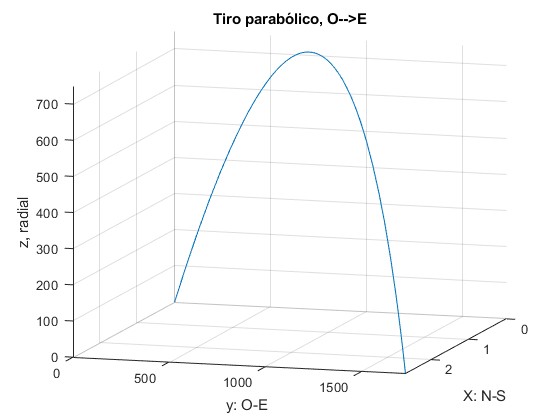
>> T T = 24.7312 >> y(T) ans = 1.7303e+03 >> x(T) ans = 2.6964
El alcance es 1730 m y la desviación hacia el sur y=2.6964 m
Fuerzas sobre la partícula en el Sistema de Referencia Local
En el Sistema de Referencia Local, las fuerzas que actúan sobre la partícula que se deja caer desde una altura h, son: el peso (en la dirección radial Z), la fuerza de Coriolis y la fuerza centrífuga. Dividiendo entre la masa m obtenemos la ecuación vectorial
Aceleración de Coriolis
La aceleración de Coriolis es
donde Ω es la velocidad angular de rotación de la Tierra y es la velocidad del cuerpo medida en el Sistema de Referencia Local. Supongamos que la posición del observador es α.
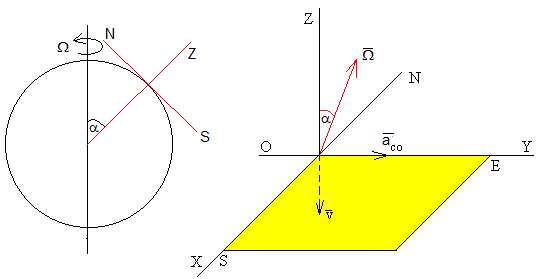
La aceleración de Coriolis en el hemisferio Norte está dirigida hacia el Este y su módulo es
ay=2Ωv·sinα
Aceleración centrífuga
Si estamos en el hemisferio Norte, en un lugar α, una partícula situada en este punto describe una circunferencia de radio r=R·sinα. La aceleración centrífuga es radial y dirigida hacia afuera, tal como se indica en la figura, su módulo es
ac=Ω2r=Ω2R·sinα
Los datos del planeta Tierra son:
- Velocidad angular de rotación Ω, una vuelta (2·π cada 24 horas (86400 s).
- El radio de la Tierra es de R=6370 km.
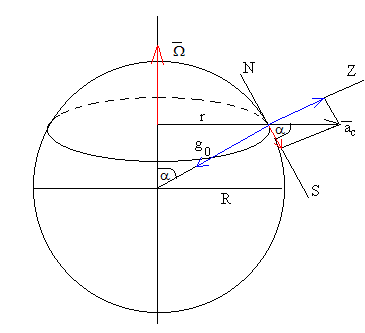
La aceleración centrífuga tiene dos componenentes:
- Componente en la dirección radial, que disminuye la aceleración g0 de la gravedad
- Componente en la dirección Norte-Sur (eje X), que desvía los cuerpos hacia el Sur. El
valor de esta componente es
ax=ac·cosα=Ω2R·cosα·sinα. Esta aceleración es nula cuando estamos en el plano ecuatorial α=90º.
g=g0-Ω2R·sin2α
La aceleración centrífuga en el ecuador α=90º, es máxima Ω2R, pero es muy pequeña comparada con g0
Ecuaciones del movimiento
En el Sistema de Referencia Local, el movimiento de un cuerpo que se deja caer, desde la posición z=h, x=0, y=0, es la composición de tres movimientos:
A lo largo del eje X, es un movimiento uniformente acelerado
A lo largo del eje Z, es un movimiento uniformente acelerado, la aceleración es de la gravedad efectiva g
A lo largo del eje Y, es acelerado (aceleración variable)
La aceleración de Coriolis ay de un cuerpo que cae es máxima en el ecuador α=90º y es nula en los polos α=0º. En el polo coinciden las direcciones de los vectores velocidad angular de rotación y la velocidad del cuerpo que cae, el producto vectorial de ambos vectores es por tanto, cero.
Si estamos situados en el plano del ecuador α=90° y el cuerpo se deja caer desde una altura de h=100 m, tenemos una desviación y=2.2 cm, que no se puede apreciar a simple vista.
R=6.378e6; %radio de la tierra en m
w=2*pi/(24*3600); %velocidad angular de rotación
h=1000; %altura
alfa=pi/6; %posición
g=9.8-w^2*R*sin(alfa)^2; %aceleración de la gravedad
t=0:0.025:sqrt(2*h/g);
z=h-g*t.^2/2; %en m
y=w*g*t.^3*sin(alfa)/3; %en m
x=w^2*R*cos(alfa)*sin(alfa)*t.^2/2; %en m
plot3(x,y,z)
grid on
xlabel('X: N-S')
ylabel('y: O-E')
zlabel('Z, radial')
title('Caída de un cuerpo sobre la superficie de la tierra')
view(107,12)
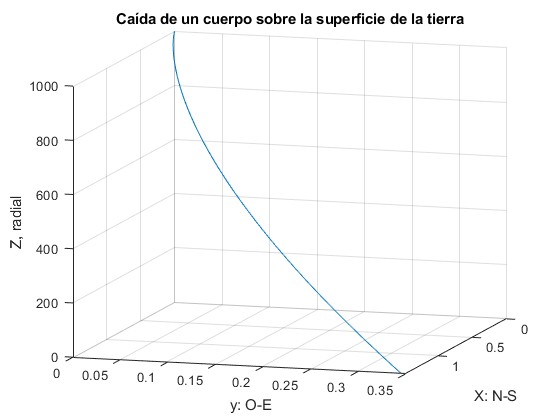
>> x(end) ans = 1.4881 >> y(end) ans = 0.3452
Los números que aparecen en este cuadro se interpretan del siguiente modo (véase la gráfica): cuando la partícula llega al suelo z=0, la desviación hacia el Sur es x=1.4881, en el código
Referencias
Eric Poisson. Advanced mechanics PHYS*3400. Lecture notes (January 2008). Department of Physics. University of Guelph.
Walter Greiner. Classical Mechanics. System of Particles and Hamiltonian Dynamics. Second Edition. Springer. pp. 11-17

