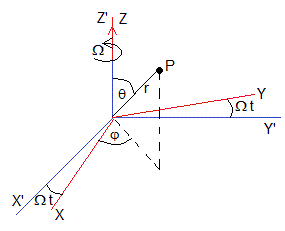
Sea S'un sistema de referencia inercial X',Y',Z' y sea S un sistema de referencia X,Y,Z en rotación. Los orígenes de ambos sistemas de referencia coinciden así como los ejes Z y Z'.

Vamos a utilizar coordenadas esféricas de modo que la posición de un punto P en el sistema S es (r, φ, θ) y el sistema inercial S' es (r', φ', θ'). Dado que el origen de S y S' es el mismo r=r', y como los ejes Z y Z' coinciden θ=θ'. Los ángulos φ y φ' están relacionados por φ'=φ+Ωt

La posición de P en el sistema inercial S' y en el sistema S en rotación son, respectivamente

${\displaystyle S\{\begin{array}{l}x=r\sin \theta \cos \phi \\ y=r\sin \theta \sin \phi \\ z=r\cos \theta \end{array}S\text{'}\{\begin{array}{l}x\text{'}=r\sin \theta \cos \phi \text{'}\\ y\text{'}=r\sin \theta \sin \phi \text{'}\\ z\text{'}=r\cos \theta \end{array}}$

Como vemos z'=z. Relacionamos utilizando notación compleja x',y' con x,y

${\displaystyle \begin{array}{l}x+iy=r\sin \theta \left(\cos \phi +i\sin \phi \right)=r\sin \theta \exp (i\phi )\\ x\text{'}+iy\text{'}=r\sin \theta \exp (i\phi \text{'})=r\sin \theta \exp (i\phi +i\Omega t)=\\ \exp (i\Omega t)·r\sin \theta \exp (i\phi )=\exp (i\Omega t)·\left(x+iy\right)\\ x\text{'}+iy\text{'}=\left(x\cos \left(\Omega t\right)-y\sin \left(\Omega t\right)\right)+i\left(y\cos \left(\Omega t\right)+x\sin \left(\Omega t\right)\right)\end{array}}$

El resultado es

${\displaystyle \{\begin{array}{l}x\text{'}=x\cos \left(\Omega t\right)-y\sin \left(\Omega t\right)\\ y\text{'}=y\cos \left(\Omega t\right)+x\sin \left(\Omega t\right)\\ z\text{'}=z\end{array}}$

Derivando con respecto del tiempo relacionamos las componentes de la velocidad en ambos sistemas de referencia

${\displaystyle \{\begin{array}{l}\frac{dx\text{'}}{dt}=\frac{dx}{dt}\cos \left(\Omega t\right)-\frac{dy}{dt}\sin \left(\Omega t\right)-\Omega \left(x\sin \left(\Omega t\right)+y\cos \left(\Omega t\right)\right)\\ \frac{dy\text{'}}{dt}=\frac{dy}{dt}\cos \left(\Omega t\right)+\frac{dx}{dt}\sin \left(\Omega t\right)-\Omega \left(y\sin \left(\Omega t\right)-x\cos \left(\Omega t\right)\right)\\ \frac{dz\text{'}}{dt}=\frac{dz}{dt}\end{array}}$

Calculamos el cuadrado del módulo de la velocidad para obtener la expresión de la energía cinética T'=mv'²/2 en términos de la energía cinética T=mv²/2 en el sistema S

${\displaystyle \begin{array}{l}\left({\left(\frac{dx\text{'}}{dt}\right)}^2+{\left(\frac{dy\text{'}}{dt}\right)}^2+{\left(\frac{dz\text{'}}{dt}\right)}^2\right)\\ =\left({\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2+{\left(\frac{dz}{dt}\right)}^2\right)-2\Omega \left(y\frac{dx}{dt}-x\frac{dy}{dt}\right)+{\Omega }^2\left(x^2+y^2\right)\end{array}}$

Sea V(x,y,z) la energía potencial de la partícula en el sistema S o V(x',y',z') en el sistema inercial S'

La lagrangiana L=T'-V de la partícula en el sistema inercial S' es

${\displaystyle \begin{array}{l}L=\frac{1}{2}m\left({\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2+{\left(\frac{dz}{dt}\right)}^2\right)-m\Omega \left(y\frac{dx}{dt}-x\frac{dy}{dt}\right)+\frac{1}{2}m{\Omega }^2\left(x^2+y^2\right)-V(x,y,z)\\ L=\frac{1}{2}m\left({\dot{x}}^2+{\dot{y}}^2+{\dot{z}}^2\right)-m\Omega \left(y\dot{x}-x\dot{y}\right)+\frac{1}{2}m{\Omega }^2\left(x^2+y^2\right)-V(x,y,z)\end{array}}$

Ecuaciones del movimiento

• Ecuación del movimiento a lo largo del eje X

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right)-\frac{\partial L}{\partial x}=0\\ m\frac{d^{2}x}{d{t}^2}-2m\Omega \frac{dy}{dt}-m{\Omega }^{2}x+\frac{\partial V}{\partial x}=0\end{array}}$

• Ecuación del movimiento a lo largo del eje Y

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{y}}\right)-\frac{\partial L}{\partial y}=0\\ m\frac{d^{2}y}{d{t}^2}+2m\Omega \frac{dx}{dt}-m{\Omega }^{2}y+\frac{\partial V}{\partial y}=0\end{array}}$

• Ecuación del movimiento a lo largo del eje Z

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{z}}\right)-\frac{\partial L}{\partial z}=0\\ m\frac{d^{2}z}{d{t}^2}+\frac{\partial V}{\partial z}=0\end{array}}$

Las tres ecuaciones se pueden expresar en una sola ecuación vectorial:

La velocidad angular de rotación $\overrightarrow{\Omega }$ , es un vector que tiene la dirección del eje Z, sentido la regla del sacacorchos, $\overrightarrow{\Omega }=\Omega \widehat{k}$

${\displaystyle \begin{array}{l}m\frac{d^2\overrightarrow{r}}{d{t}^2}=-\left(\frac{\partial V}{\partial x}\widehat{i}+\frac{\partial V}{\partial y}\widehat{j}+\frac{\partial V}{\partial z}\widehat{k}\right)+2m\left(\Omega \frac{dy}{dt}\widehat{i}-\Omega \frac{dx}{dt}\widehat{j}\right)+m({\Omega }^{2}x\widehat{i}+{\Omega }^{2}y\widehat{j})\hfill \\ m\frac{d^2\overrightarrow{r}}{d{t}^2}=-\overrightarrow{\nabla }V-2m\overrightarrow{\Omega }\times \frac{d\overrightarrow{r}}{dt}-m\overrightarrow{\Omega }\times (\overrightarrow{\Omega }\times \overrightarrow{r})\hfill \end{array}}$

El primer término es la fuerza aplicada, el segundo término es la fuerza de Coriolis y el tercer término la fuerza centrífuga.

${\displaystyle m\frac{d^2\overrightarrow{r}}{d{t}^2}=\overrightarrow{F_a}+\overrightarrow{F_{co}}+\overrightarrow{F_c}}$

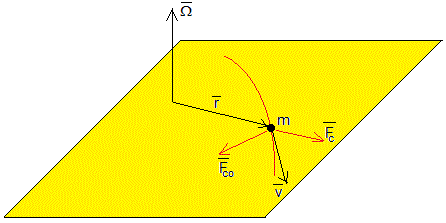
La fuerza centrífuga $\overrightarrow{F_c}$ tiene dirección radial, es la responsable del incremento del radio de la trayectoria y la fuerza de Coriolis $\overrightarrow{F_{co}}$ es perpendicular a la velocidad $\overrightarrow{v}=\frac{d\overrightarrow{r}}{dt}$ es responsable de su curvatura.

Movimiento de una partícula a lo largo del eje X

El ejemplo más sencillo es el de una partícula se lanza con velocidad v₀ desde el origen a lo largo del eje X sobre una plataforma en rotación con velocidad angular constante Ω. Vamos a determinar la trayectoria vista por el observador inercial.

En este caso V(x,y,z)=0. El movimiento tiene lugar en el plano XY de la plataforma. Las ecuaciones del movimiento son

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}-2\Omega \frac{dy}{dt}-{\Omega }^{2}x=0\\ \frac{d^{2}y}{d{t}^2}+2\Omega \frac{dx}{dt}-{\Omega }^{2}y=0\end{array}}$

Utilizando notación compleja

${\displaystyle \begin{array}{l}\xi =x+iy\\ \frac{d^2\xi }{d{t}^2}-2\Omega \left(\frac{dy}{dt}-i\frac{dx}{dt}\right)-{\Omega }^2\xi =0\\ \frac{d^2\xi }{d{t}^2}+2\Omega i\left(\frac{dx}{dt}+i\frac{dy}{dt}\right)-{\Omega }^2\xi =0\\ \frac{d^2\xi }{d{t}^2}+2\Omega i\frac{d\xi }{dt}-{\Omega }^2\xi =0\end{array}}$

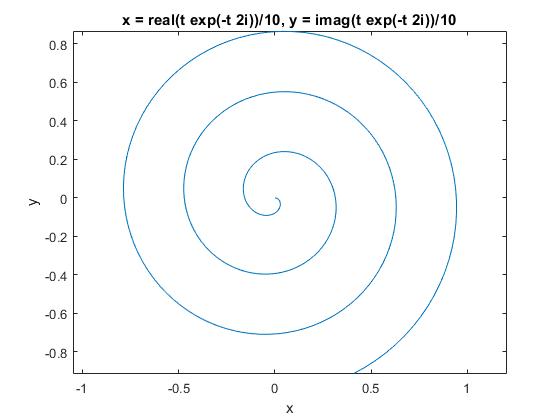
Resolvemos la ecuación diferencial utilizando la función MATLAB dsolve

>> syms W x;
>> z=dsolve('D2x+2*1i*W*Dx-W^2*x=0','Dx(0)=0.1','x(0)=0');
>> z=subs(z,W,2);
>> ezplot(real(z),imag(z),[0,10])

Las raíces de la ecuación característica son

${\displaystyle s^2+2\Omega is-{\Omega }^2=0\{\begin{array}{l}{s}_1=-i\Omega \\ s_2=-i\Omega \end{array}}$

La solución de esta ecuación diferencial lineal con raíces repetidas es

${\displaystyle \begin{array}{l}\xi =C\exp (-i\Omega t)+Dt\exp (-i\Omega t)=\left(C+Dt\right)\exp (-i\Omega t)\\ \frac{d\xi }{dt}=-i\Omega \left(C+Dt\right)\exp (-i\Omega t)+D\exp (-i\Omega t)=\left(D-i\Omega \left(C+Dt\right)\right)\exp (-i\Omega t)\end{array}}$

Donde C y D son números complejos cuya parte real e imaginaria se determinan a partir de las condiciones iniciales:

${\displaystyle t=0\{\begin{array}{l}x=x_0,y=y_0\\ \frac{dx}{dt}=v_{0x},\frac{dy}{dt}=v_{0y}\end{array}\{\begin{array}{l}{\xi }_0=x_0+i{y}_0\\ {\frac{d\xi }{dt}|}_0=v_{0x}+i{v}_{0y}\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}C=x_0+i{y}_0\hfill \\ D=\left(v_{0x}-\Omega y_0\right)+i\left(v_{0y}+\Omega x_0\right)\hfill \end{array}}$

Las expresiones de x e y en función del tiempo son:

${\displaystyle \begin{array}{l}x=\left(C_r+D_{r}t\right)\cos (\Omega t)+\left(C_i+D_{i}t\right)\sin (\Omega t)\\ y=-\left(C_r+D_{r}t\right)\sin (\Omega t)+\left(C_i+D_{i}t\right)\cos (\Omega t)\end{array}}$

Una plataforma de radio R=1, gira con velocidad angular Ω=0.5 rad/s. Las partículas parten del origen con velocidades v_0x=0, y v_0y=0.1, 0.3, 0.6 m/s, respectivamente

El programa calcula el instante en el que la partícula alcanza el borde de la plataforma, mediante la función fzero de MATLAB

${\displaystyle \{\begin{array}{l}x(t)=\left(x_0+v_{0x}t\right)\cos \left(\Omega t\right)+\left(v_{0y}+\Omega x_0\right)t\sin \left(\Omega t\right)\\ y(t)=-\left(x_0+v_{0x}t\right)\sin \left(\Omega t\right)+\left(v_{0y}+\Omega x_0\right)t\cos \left(\Omega t\right)\end{array}}$

W=0.5; %velocidad angular de rotación
v0x=0;
x0=0; %posición inicial (origen)
R=1; %radio de la plataforma
hold on
for v0y=[0.1,0.3,0.6]
    x=@(t) (x0+v0x*t).*cos(W*t)+(v0y+W*x0)*t.*sin(W*t);
    y=@(t) -(x0+v0x*t).*sin(W*t)+(v0y+W*x0)*t.*cos(W*t);
    r=@(t) sqrt(x(t).^2+y(t).^2);
    g=@(t) r(t)-R;
    tf=fzero(g,[1,50]);
    fplot(x,y,[0,tf])
end
fplot(@(th) cos(th), @(th) sin(th),[0,2*pi],'color','k') %plataforma
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
title('Movimiento sobre una plataforma giratoria')

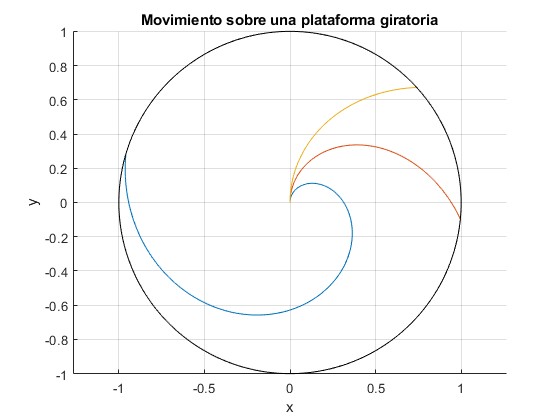
Obtenemos la misma trayectoria que en la página Movimiento relativo de rotación uniforme

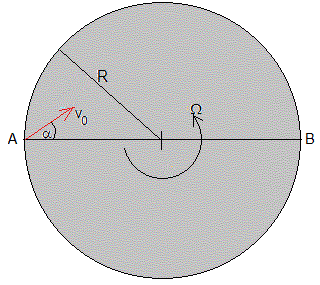
Otro ejemplo estudiado en la misma página. La partícula sale de la posición A, x₀=-R, y₀=0, y llega a B (R, 0) después de un tiempo t=2π/Ω

Las condiciones finales en B en el instante t=2π/Ω implican las dos relaciones

${\displaystyle \begin{array}{l}R=C_r+D_r\frac{2\pi }{\Omega }\hfill \\ 0=C_i+D_i\frac{2\pi }{\Omega }\hfill \end{array}}$

Las condiciones iniciales en A el instante t=0, implican

${\displaystyle \begin{array}{l}C=-R\hfill \\ D=v_0\cos \alpha +i(v_0\sin \alpha -\Omega R)\hfill \end{array}}$

C_r=-R, C_i=0, D_i=0, por lo que v₀sinα=ΩR. La velocidad del móvil respecto al Sistema de Referencia Intercial tiene la dirección del diámetro AB. La posición (x,y) en función del tiempo t es

${\displaystyle \begin{array}{l}x=R\left(\frac{\Omega t}{\pi }-1\right)\cos (\Omega t)\hfill \\ y=-R\left(\frac{\Omega t}{\pi }-1\right)\sin (\Omega t)\hfill \end{array}}$

R=1; %radio del disco
W=1; %velocidad angular de rotación
x=@(t) R*(W*t/pi-1).*cos(W*t);
y=@(t) -R*(W*t/pi-1).*sin(W*t);
fplot(x,y,[0,2*pi])
axis equal
grid on
xlabel('x')
ylabel('y')
title('Movimiento sobre una plataforma en rotación')

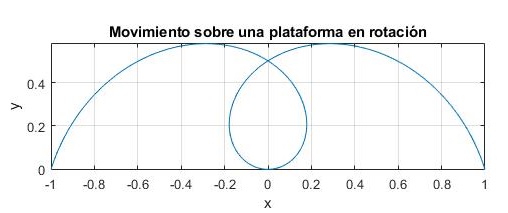
Movimiento de una partícula unida a un muelle elástico

Vamos a estudiar el comportamiento de una partícula de masa m unida a uno de los extremos de un muelle elástico de constante k mientras que el otro está sujeto al eje de la plataforma en rotación. Si el muelle está sobre la plataforma, en el plano XY, la energía potencial del muelle será

${\displaystyle V(x,y)=\frac{1}{2}k\left(x^2+y^2\right)=\frac{1}{2}m{\omega }^2\left(x^2+y^2\right)}$

Las ecuaciones del movimiento para este sistema son

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}-2\Omega \frac{dy}{dt}+\left({\omega }^2-{\Omega }^2\right)x=0\\ \frac{d^{2}y}{d{t}^2}+2\Omega \frac{dx}{dt}+\left({\omega }^2-{\Omega }^2\right)y=0\\ \frac{d^{2}z}{d{t}^2}=0\end{array}}$

La trayectoria de la partícula está confinado al plano XY de la plataforma en rotación. Utilizando notación compleja ξ=x+iy

${\displaystyle \begin{array}{l}\xi =x+iy\\ \frac{d^2\xi }{d{t}^2}-2\Omega \left(\frac{dy}{dt}-i\frac{dx}{dt}\right)+\left({\omega }^2-{\Omega }^2\right)\xi =0\\ \frac{d^2\xi }{d{t}^2}+2\Omega i\frac{d\xi }{dt}+\left({\omega }^2-{\Omega }^2\right)\xi =0\end{array}}$

Resolvemos la ecuación diferencial utilizando la función MATLAB dsolve

Probamos el siguiente ejemplo:

• Velocidad angular de rotación, Ω=0.8
• Frecuencia angular (vibración) k/m=ω²=1
• Posición inicial, ξ₀=1
• Velocidad inicial, (dξ/dt)₀=0.4·i

>> syms w W x;
>> z=dsolve('D2x+2*1i*W*Dx+(w^2-W^2)*x=0','Dx(0)=0+0.4*1i','x(0)=1+0*1i');
>> z=subs(z,{w,W},{1,0.8});
>> ezplot(real(z),imag(z),[0,40])

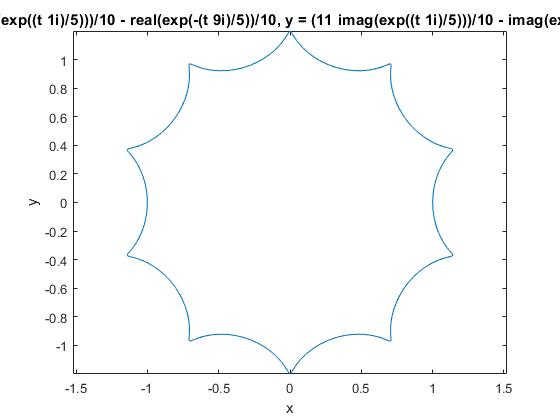
Las raíces de la ecuación característica

${\displaystyle s^2+2\Omega is+\left({\omega }^2-{\Omega }^2\right)=0\{\begin{array}{l}{s}_1=i\left(\omega -\Omega \right)\\ s_2=-i\left(\omega +\Omega \right)\end{array}}$

La solución de la ecuación diferencial es

${\displaystyle \xi =C\exp \left(i(\omega -\Omega )t\right)+D\exp \left(-i(\omega +\Omega )t\right)}$

Donde C y D son números complejos cuya parte real e imaginaria se determinan a partir de las condiciones iniciales:

${\displaystyle t=0\{\begin{array}{l}\frac{dx}{dt}=v_{0x},\frac{dy}{dt}=v_{0y}\\ x=x_0,y=y_0\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}C=\frac{1}{2}\left(\left(1+\frac{\Omega }{\omega }\right)x_0+\frac{v_{0y}}{\omega }\right)+i\left(\left(1+\frac{\Omega }{\omega }\right)y_0-\frac{v_{0x}}{\omega }\right)\\ D=\frac{1}{2}\left(\left(1-\frac{\Omega }{\omega }\right)x_0-\frac{v_{0y}}{\omega }\right)+i\left(\left(1-\frac{\Omega }{\omega }\right)y_0+\frac{v_{0x}}{\omega }\right)\end{array}}$

La posición de la partícula en la plataforma, sus coordenadas x e y en función del tiempo t son:

${\displaystyle \begin{array}{l}x=C_r\cos (\omega -\Omega )t+D_r\cos (\omega +\Omega )t-C_i\sin (\omega -\Omega )t+D_i\sin (\omega +\Omega )t\\ y=C_i\cos (\omega -\Omega )t+D_i\cos (\omega +\Omega )t+C_r\sin (\omega -\Omega )t-D_r\sin (\omega +\Omega )t\end{array}}$

Donde C_r es la parte real del coeficiente C, C_i es la parte imaginaria y lo mismo cabe decir del coeficiente D

Probamos el siguiente ejemplo:

• Velocidad angular de rotación, Ω=0.25
• Frecuencia angular (vibración) k/m=ω²=1
• Posición inicial, x₀=1, y₀=0
• Velocidad inicial, v_0x=0, v_0y=0

w=1;  %sqrt(k/m)
W=0.25;  %velocidad rotación
x0=1;   %posición inicial
y0=0;
vx0=0; %velocidad inicial
vy0=0;
%coeficientes
C=((1+W/w)*x0+vy0/w+1i*((1+W/w)*y0-vx0/w))/2;
D=((1-W/w)*x0-vy0/w+1i*((1-W/w)*y0+vx0/w))/2;
x=@(t) real(C)*cos((w-W)*t)+real(D)*cos((w+W)*t)-imag(C)*sin((w-W)*t)+
imag(D)*sin((w+W)*t);
y=@(t) imag(C)*cos((w-W)*t)+imag(D)*cos((w+W)*t)+real(C)*sin((w-W)*t)-
real(D)*sin((w+W)*t);
fplot(x,y,[0,40])
grid on
axis equal
xlabel('x')
ylabel('y')
title('Muelle sobre una plataforma en rotación')

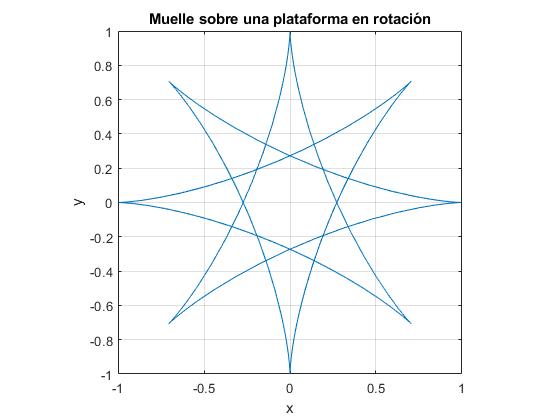
Trayectoria circular

Cuando y₀=0, y v_0x=0, C_i=0, y D_i=0.

${\displaystyle \begin{array}{l}x=C_r\cos (\omega -\Omega )t+D_r\cos (\omega +\Omega )t\hfill \\ \begin{array}{l}y=C_r\sin (\omega -\Omega )t-D_r\sin (\omega +\Omega )t\\ x^2+y^2=C_r^2+D_r^2+2C_r{D}_r\cos (2\omega t)\end{array}\hfill \end{array}}$

La trayectoria es circular centrada en el origen (0,0) cuando C_r=0, $v_{0x}=-\left(\omega +\Omega \right)x_0$ o D_r=0, $v_{0y}=\left(\omega -\Omega \right)x_0$

w=1;  %sqrt(k/m)
W=0.7;  %velocidad rotación
x0=1;   %posición inicial
y0=0;
vx0=0; %velocidad inicial
vy0=-(w+W)*x0;
%coeficientes
Cr=(1+W/w)*x0+vy0/w;
Dr=(1-W/w)*x0-vy0/w;
x=@(t) Cr*cos((w-W)*t)+Dr*cos((w+W)*t);
y=@(t) Cr*sin((w-W)*t)-Dr*sin((w+W)*t);
fplot(x,y,[0,40])
grid on
axis equal
xlabel('x')
ylabel('y')
title('Muelle sobre una plataforma en rotación')

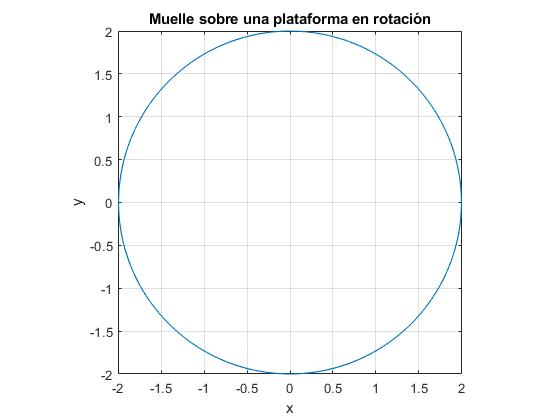
Cuando Ω=ω la trayectoria es circular

${\displaystyle \begin{array}{l}x-C_r=D_r\cos \left(2\omega t\right)+D_i\sin \left(2\omega t\right)\\ y-C_i=D_i\cos \left(2\omega t\right)-D_r\sin \left(2\omega t\right)\end{array}}$

Elevando al cuadrado y sumando

${\displaystyle {\left(x-C_r\right)}^2+{\left(y-C_i\right)}^2=D_i^2+D_r^2}$

Con los datos del ejemplo, C_r=1.2, C_i=0, (centro de la circunferencia). D_r=-0.2, D_i=0, el radio es 0.2

Actividades

Especificamos los parámetros del sistema

• La velocidad angular de rotación, el control titulado Velocidad rotación Ω
• El cociente ω²=k/m, donde k es la constante del muelle y m la masa de la partícula se ha fijado en ω=1

Especificamos las condiciones iniciales

• La posición inicial x₀ e y₀, en los controles titulados Posición, X y Posición, Y
• La velocidad inicial (dx/dt)₀ e (dy/dt)₀, en los controles titulados Velocidad, X y Velocidad, Y

Si la trayectoria aparece grande o se ve pequeña, se puede reducir o aumentar la escala para ajustarla a la ventana gráfica, en el control titulado Escala

Se sugiere al lector probar los siguientes casos: Ω=1, y Ω=0.2

La velocidad angular de rotación Ω no es constante

Cuando la velocidad angular de rotación Ω no es constante, hay que añadir una fuerza de inercia más, denominada fuerza de Euler $-m\frac{d\overrightarrow{\Omega }}{dt}\times \overrightarrow{r}$

Sobre la partícula actúan: la fuerza que ejerce el muelle, la fuerza de Coriolis, la centrífuga y la de Euler. La ecuación del movimiento de la partícula es

${\displaystyle \begin{array}{l}\begin{array}{l}m\frac{d^2\overrightarrow{r}}{d{t}^2}=-\overrightarrow{\nabla }V-2m\left(\overrightarrow{\Omega }\times \frac{d\overrightarrow{r}}{dt}\right)-m\overrightarrow{\Omega }\times \left(\overrightarrow{\Omega }\times \overrightarrow{r}\right)-m\frac{d\overrightarrow{\Omega }}{dt}\times \overrightarrow{r}\hfill \end{array}\\ m\frac{d^2\overrightarrow{r}}{d{t}^2}=-\left(\frac{\partial V}{\partial x}\widehat{i}+\frac{\partial V}{\partial y}\widehat{j}+\frac{\partial V}{\partial z}\widehat{k}\right)+2m\left(\Omega \frac{dy}{dt}\widehat{i}-\Omega \frac{dx}{dt}\widehat{j}\right)+m\left({\Omega }^{2}x\widehat{i}+{\Omega }^{2}y\widehat{j}\right)-m\left(-y\frac{d\Omega }{dt}\widehat{i}+x\frac{d\Omega }{dt}\widehat{j}\right)\end{array}}$

Para una partícula unida a un muelle elástico, hay que resolver el sistema de dos ecuaciones diferenciales

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}-2\Omega \frac{dy}{dt}+({\omega }^2-{\Omega }^2)x-\frac{d\Omega }{dt}y=0\hfill \\ \frac{d^{2}y}{d{t}^2}+2\Omega \frac{dx}{dt}+({\omega }^2-{\Omega }^2)y+\frac{d\Omega }{dt}x=0\hfill \end{array}}$

Los dos términos adicionales y·dΩ/dt y x·dΩ/dt corresponden a la fuerza de Euler

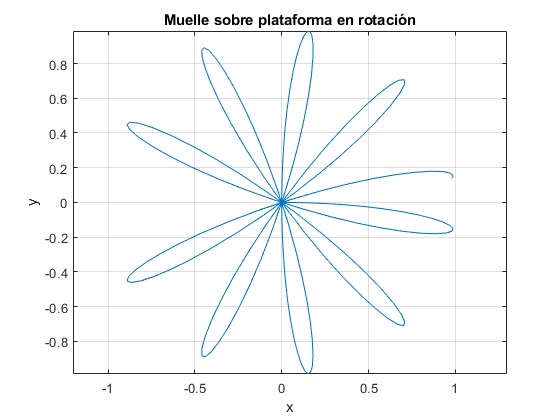
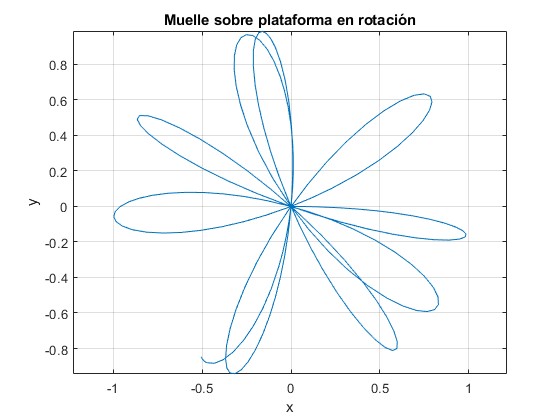
Supongamos que la velocidad angular de rotación varía linealmente con el tiempo, Ω=Ω₀+kt.

Resolvemos numéricamente el sistema de dos ecuaciones diferenciales utilizando el procedimiento ode45 de MATLAB con las siguientes condiciones iniciales, para t=0, x=1, dx/dt=0, y=0, dy/dt=0

W0=0.1; %velocidad angular de rotación
w=1; %frecuencia angular
k=5e-3;
%x(1) es x, x(2) es dx/dt, x(3) es y y x(4) es dy/dt
fg=@(t,x)[x(2); ((W0+k*t)^2-w^2)*x(1)+2*(W0+k*t)*x(4)+k*x(3); x(4); 
((W0+k*t)^2-w^2)*x(3)-2*(W0+k*t)*x(2)-k*x(1)];
[~,x]=ode45(fg,[0,30],[1, 0, 0, 0]);
plot(x(:,1),x(:,3))
axis equal
grid on
xlabel('x')
ylabel('y');
title('Muelle sobre plataforma en rotación')

• k=0. Sin fuerza de Euler



• k=0.005. Con fuerza de Euler

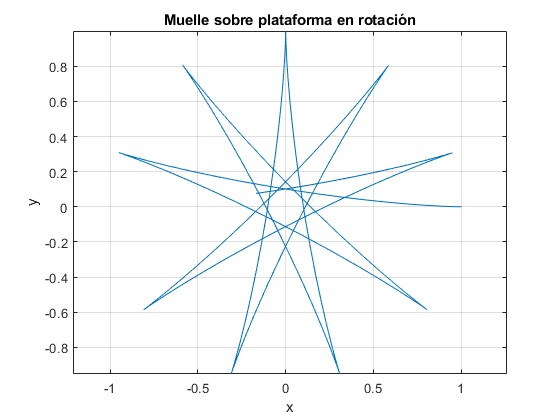
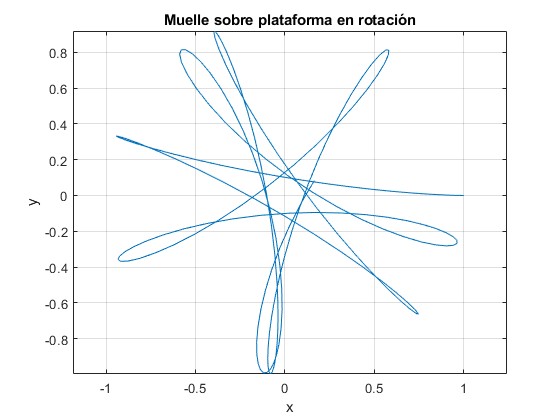
Cambiamos las condiciones iniciales, para t=0, x=0, dx/dt=1, y=0, dy/dt=0

• k=0. Sin fuerza de Euler



• k=0.005. Con fuerza de Euler

Referencias

J Barcelos-Neto, M B Dias da Silva. An example of motion in a rotating frame. Eur. J. Phys. 10 (1989) pp. 305-308

Vladimir Ivchenko. On the "Forgoten" Euler Inertial Force. Resonance, Volume 29, Issue 6, June 2024. pp. 815-823