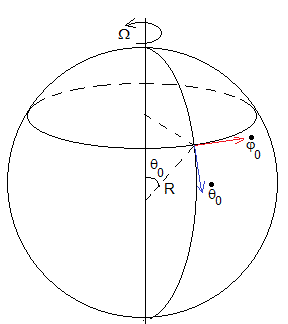
Movimiento relativo sobre la superficie de la Tierra
La ecuación del movimiento de una partícula de masa m que se mueve sobre la superficie de la Tierra, en movimiento de rotación con velocidad angular constante Ω es:
Donde es la fuerza aplicada. Si el eje de giro coincide con el eje Z, es decir, si el vector velocidad angular lleva esta la dirección, entonces
Una partícula situada sobre la superficie de la Tierra está sometida a dos fuerzas de dirección radial y de sentido contrario, el peso mg y la reacción de la superficie T
Las ecuaciones del movimiento a lo largo de los tres ejes son:
El cuerpo se moverá sobre la superficie de la Tierra siempre que T>0. Expresamos el sistema de tres ecuaciones diferenciales en coordenadas polares. Designamos R como radio de la Tierra, supuesta esférica
Calculamos la derivada primera de x, y, z respecto del tiempo t
Calculamos la derivada segunda de x, y, z respecto del tiempo t
Introducimos estos resultados en las ecuaciones del movimiento. Despejamos T en la tercera ecuación y la sustituimos en las dos primeras. Se simplifica, la masa m y el radio R y nos queda un sistema de dos ecuaciones diferenciales
Despejamos en este sistema de dos ecuaciones,las derivadas segundas, y
- Multiplicamos la primera ecuación por cosφ, la segunda por sinφ y las sumamos
- Multiplicamos la primera ecuación por -sinφ, la segunda por cosφ y las sumamos
Nos queda el siguiente sistema de dos ecuaciones diferenciales
Que se resuelve por procedimientos numéricos con las siguientes condiciones iniciales
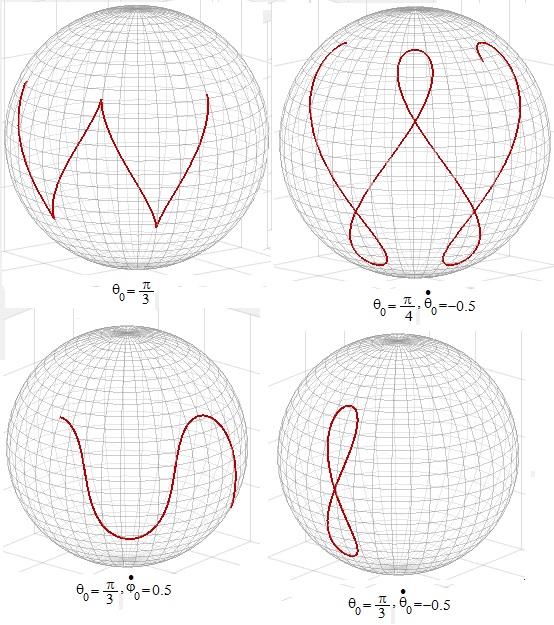
Se obtiene una gran variedad de trayectorias modificando las condiciones iniciales. Fijamos la posición de lanzamiento: θ0=π/3 y φ0=0. Modificamos la velocidad inicial:
- Hacia el este, ,
- Hacia el sur, ,
- Hacia el oeste, ,
- Hacia el norte, ,
En el código, el vector
La partícula se mantiene sobre la superficie de la Tierra siempre que T≥0
En caso contrario, se podría imaginar que una fuerza en dirección radial mantendría la partícula sobre la superficie de la Tierra.
Creamos un script, para trazar las trayectorias de la partícula sobre la superficie esférica, integrando el sistema de dos ecuaciones diferenciales mediante ode45. En la figura (más abajo), se representa la trayectoria seguida por la partícula cuando se lanza hacia el norte con velocidad 0.5
R=1; %radio de la Tierra
W=1; %velocidad angular de rotación
x0=[pi/3,-0.5,0,0]; %condiciones iniciales: [theta, dtheta/dt, phi,dphi/dt]
tspan=[0,7];
% x(1)=theta, x(2)=dtheta/dt,x(3)=phi, x(4)=dphi/dt
fg=@(t,x)[x(2); sin(x(1))*cos(x(1))*(x(4)^2+2*W*x(4)+W^2); x(4);
-2*cos(x(1))*(W*x(2)+x(2)*x(4))/sin(x(1))];
[t,x]=ode45(fg,tspan,x0);
xp=R*sin(x(:,1)).*cos(x(:,3));
yp=R*sin(x(:,1)).*sin(x(:,3));
zp=R*cos(x(:,1));
%esfera
phi=linspace(0,pi,30);
theta=linspace(0,2*pi,40);
[phi,theta]=meshgrid(phi,theta);
x=R*sin(phi).*cos(theta);
y=R*sin(phi).*sin(theta);
z=R*cos(phi);
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0.6,0.6,0.6],'EdgeAlpha',0.5,'FaceAlpha',0.5)
axis equal
%trayectoria
h1=line(xp,yp,zp);
set(h1,'Color',[.7,0,0],'LineWidth',1.5)
view (130,20)
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
zlabel('z')
title('Movimiento sobre la superficie de la Tierra')
Referencias
A. Amengual. Noninertial trajectories on a fast rotating planet. Am. J. Phys. 68 (12) December 2000, pp. 1106-1108

