Método de los multiplicadores de Lagrange

Sea z=f(x₁,x₂,x₃,...x_n) una función de n variables. Supongamos que las variables están relacionados por m<n condiciones complementarias

g₁(x₁,x₂,x₃,...x_n)=0
g₂(x₁,x₂,x₃,...x_n)=0
.........
g_m(x₁,x₂,x₃,...x_n)=0

Consideremos una nueva función F(x₁,x₂,x₃,...x_n)

${\displaystyle F=f+{\displaystyle \sum _{i=1}^m{\lambda }_i{g}_i}}$

donde λ_i son factores indeterminados

Formamos el sistema de ecuaciones

${\displaystyle \{\begin{array}{l}\frac{\partial F}{\partial x_1}=0\\ \frac{\partial F}{\partial x_2}=0\\ \mathrm{....}\\ \frac{\partial F}{\partial x_n}=0\end{array}}$

Que junto a m condiciones, g_i(x₁,x₂,x₃,...x_n)=0, determinan los valores de los m parámetros λ₁, λ₂...λ_m y las n coordenadas x₁, x₂...x_n de los posibles puntos extremos (máximos o mínimos) condicionados de la función z=f(x₁,x₂,x₃,...x_n)

Hallar el extremo de la función, $f(x,y)={\cos }^{2}x+{\cos }^{2}y$, con la condición, y-x=π/4

Formamos la función de Lagrange

${\displaystyle F(x,y)={\cos }^{2}x+{\cos }^{2}y+\lambda \left(y-x-\frac{\pi }{4}\right)}$

El sistema de ecuaciones para determinar el parámetro λ y las coordenadas de los posibles puntos extremos (x,y) es

${\displaystyle \{\begin{array}{l}\frac{\partial F}{\partial x}=-2\cos x·\sin x-\lambda =0\\ \frac{\partial F}{\partial y}=-2\cos y·\sin y+\lambda =0\\ y-x-\frac{\pi }{4}=0\end{array}}$

La solución de este sistema de ecuaciones es

${\displaystyle \{\begin{array}{l}\sin \left(2x\right)=-\lambda \\ \sin \left(2y\right)=\lambda \\ y-x=\frac{\pi }{4}\end{array}}$

Teniendo en cuenta la relación trigonométrica

${\displaystyle \sin \left(2A\right)+\sin \left(2B\right)=2\left(\sin \left(A+B\right)\cos \left(A-B\right)\right)}$

sin(x+y)cos(y-x)=0
sin(x+y)·cos(π/4)=0
x+y=nπ, n=0, ±1,±2...

que con la ecuación y-x=π/4, da lugar a los siguientes puntos

${\displaystyle x=n\frac{\pi }{2}-\frac{\pi }{8}y=n\frac{\pi }{2}+\frac{\pi }{8}n=\mathrm{0,}\pm \mathrm{1,}\pm \mathrm{2...}}$

Hallar el extremo condicionado de la función f(x,y,z)=xyz con la condición de que

${\displaystyle \{\begin{array}{l}{g}_1(x,y,z)=x+y-z-3=0\\ g_2(x,y,z)=x-y-z-8=0\end{array}}$

Formamos la función de Lagrange

${\displaystyle F(x,y,z)=xyz+{\lambda }_1\left(x+y-z-3\right)+{\lambda }_2\left(x-y-z-8\right)}$

El sistema de ecuaciones para determinar los λ y las coordenadas de los posibles puntos de extremo es

${\displaystyle \{\begin{array}{l}\frac{\partial F}{\partial x}=yz+{\lambda }_1+{\lambda }_2=0\\ \frac{\partial F}{\partial y}=xz+{\lambda }_1-{\lambda }_2=0\\ \frac{\partial F}{\partial z}=xy-{\lambda }_1-{\lambda }_2=0\end{array}}$

Que junto con las dos condiciones, dan lugar a 5 ecuaciones con cinco incógnitas, cuya solución es

${\displaystyle x=\frac{11}{4}y=-\frac{5}{2}z=-\frac{11}{4}{\lambda }_1=\frac{11}{32}{\lambda }_2=-\frac{231}{32}}$

Ecuación de Euler-Lagrange

Dada una función $f(x,y,\dot{y})$, tenemos que encontrar la curva y=y(x) que hace que la integral

${\displaystyle I(y)={\displaystyle \underset{x_1}{\overset{x_2}{\int }}f(x,y,\dot{y})dx}}$

denominado funcional, sea un extremo (máximo o mínimo), con las condiciones de contorno

${\displaystyle \{\begin{array}{l}y(x_1)=y_1\\ y(x_2)=y_2\end{array}}$

El símbolo $\dot{y}=\frac{dy}{dx}$

La curva y=y(x) deberá cumplir la ecuación de Euler-Lagrange

${\displaystyle \frac{\partial f}{\partial y}-\frac{d}{dx}\left(\frac{\partial f}{\partial \dot{y}}\right)=0}$

o bien, la equivalente

${\displaystyle \frac{\partial f}{\partial x}-\frac{d}{dx}\left(f-\frac{\partial f}{\partial \dot{y}}\dot{y}\right)=0}$

La demostración se puede encontrar en los textos de Matemáticas que incluyan un capítulo dedicado al cálculo de variaciones. Como veremos en los ejemplos

• Cuando f no depende de y, la primera ecuación diferencial se convierte en

${\displaystyle \frac{\partial f}{\partial \dot{y}}=C_1}$

• Cuando f no depende de x, la segunda ecuación diferencial se convierte en

${\displaystyle f-\frac{\partial f}{\partial \dot{y}}\dot{y}=C_1}$

donde C₁ es una constante a determinar

¿En qué curva puede alcanzar su extremo el funcional

${\displaystyle I(y)={\displaystyle \underset{1}{\overset{2}{\int }}\left({\dot{y}}^2-2xy\right)}dx}$

con las condiciones de contorno

y(1)=0 , y(2)=-1?

Aplicamos la ecuación Euler-Lagrange a la función $f(x,y,\dot{y})={\dot{y}}^2-2xy$. Las derivadas parciales valen

${\displaystyle \begin{array}{l}\frac{\partial f}{\partial \dot{y}}=2\dot{y}\frac{\partial f}{\partial y}=-2x\\ \frac{d}{dx}\left(\frac{\partial f}{\partial \dot{y}}\right)=2\ddot{y}\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}\frac{d^{2}y}{d{x}^2}=-x\\ \frac{dy}{dx}=-\frac{x^2}{2}+C_1\\ y=-\frac{x^3}{6}+C_{1}x+C_2\end{array}}$

Con las condiciones de contorno determinamos C₁=1/6 y C₂=0. El extremo puede alcanzarse sólamente en la curva

${\displaystyle y=\frac{x}{6}\left(1-x^2\right)}$

Entre las curvas que unen los puntos A(1,3) y B(2,5), hallar la curva y=y(x) en la que puede alcanzar su extremo la funcional

${\displaystyle I(y)={\displaystyle \underset{1}{\overset{2}{\int }}\dot{y}(1+x^2\dot{y})dx}}$

En este caso, la función $f(x,y,\dot{y})=\dot{y}(1+x^2\dot{y})$, no depende de y, por lo que ∂f/∂y=0. La ecuación de Euler-Lagrange es

${\displaystyle \begin{array}{l}\frac{\partial f}{\partial \dot{y}}=1+2x^2\dot{y}\\ 1+2x^2\frac{dy}{dx}=C_1\end{array}}$

Cuya solución es

${\displaystyle \begin{array}{l}1+2x^2\frac{dy}{dx}=C_1\\ \frac{dy}{dx}=\frac{C_1-1}{2x^2}\\ y=\frac{1-C_1}{2x}+C_2\end{array}}$

Con las condiciones de contorno determinamos C₁=9 y C₂=7. El extremo puede alcanzarse sólo en la curva

${\displaystyle y=7-\frac{4}{x}}$

Entre las curvas que unen los puntos A(x₁,y₁) y B (x₂,y₂) hallar la curva y=y(x) en la que puede alcanzar su extremo la funcional

${\displaystyle I(y)={\displaystyle \underset{x_1}{\overset{x_2}{\int }}\frac{\sqrt{1+{\dot{y}}^2}}{y}dx}}$

En este caso, la función

${\displaystyle f(x,y,\dot{y})=\frac{\sqrt{1+{\dot{y}}^2}}{y}}$

no depende de x. Utilizamos la segunda forma de la ecuación de Euler-Lagrange

${\displaystyle \begin{array}{l}f-\frac{\partial f}{\partial \dot{y}}\dot{y}=C_1\\ \frac{\sqrt{1+{\dot{y}}^2}}{y}-\frac{{\dot{y}}^2}{y\sqrt{1+{\dot{y}}^2}}=C_1\end{array}}$

La solución es

${\displaystyle \begin{array}{l}y\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}=C_1\\ {\displaystyle \int \frac{y·dy}{\sqrt{C_1^2-y^2}}}=x+C_2\\ \sqrt{C_1^2-y^2}=x+C_2\\ {\left(x+C_2\right)}^2+y^2=C_1^2\end{array}}$

Con las condiciones de contorno determinamos C₁y C₂. El extremo puede alcanzarse sólo en la curva y=y(x) que es una circunferencia con centro en el eje X que pasa por los puntos A(x₁,y₁) y B(x₂,y₂)

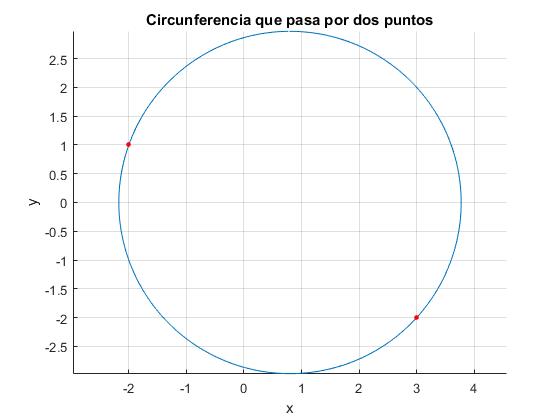
Como ejemplo, consideremos la circunferencia con centro en el eje X que pasa por los puntos A(-2,1), B(3,-2).

Calculamos el radio C₁ y el centro C₂, resolviendo el sistema de dos ecuaciones con dos incógnitas y las guardamos en las variables k1 y k2

>> syms x y c1 c2 t;
>> eq=(x+c2)^2+y^2-c1^2;
>> eq1=subs(eq,{x,y},{-2,1});
>> eq2=subs(eq,{x,y},{3,-2});
>> [k1,k2]=solve(eq1,eq2,c1,c2)
k1 =
 -221^(1/2)/5
  221^(1/2)/5
k2 =
 -4/5
 -4/5

Representamos la circunferencia y los puntos por los que pasa

>> hold on
>> fplot(-k2(1)+k1(2)*cos(t),k1(2)*sin(t),[0,2*pi])
>> plot(-2,1,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
>> plot(3,-2,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
>> axis equal
>> xlabel('x')
>> ylabel('y')
>> title('Circunferencia que pasa por dos puntos')
>> grid on
>> hold off

Extremo condicionado

En esta sección añadimos condiciones al extremo de la funcional de la sección anterior, resolveremos problemas de extremo condicionado. El más interesante se denomina problema de Dido

Ejemplo 1

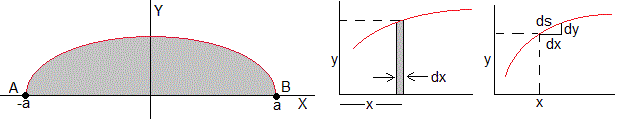
Entre todas las curvas cerradas de longitud l que pasan por los puntos A(-a,0) y B(a,0), hallar la curva y=y(x) que encierra el área máxima.

El problema se reduce a calcular el extremo de la funcional (área bajo la curva)

${\displaystyle A(y)={\displaystyle \underset{-a}{\overset{a}{\int }}y(x)·dx}}$

Con las condiciones de contorno y(-a)=0, e y(a)=0, y la condición complementaria

${\displaystyle L(y)={\displaystyle \underset{-a}{\overset{a}{\int }}ds}={\displaystyle \underset{-a}{\overset{a}{\int }}\sqrt{d{x}^2+d{y}^2}=}{\displaystyle \underset{-a}{\overset{a}{\int }}\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}·dx}=ll>2a}$

Formamos la función auxiliar, dependiente de un parámetro λ, $F(x,y,\dot{y})=y+\lambda \sqrt{1+{\dot{y}}^2}$. Aplicamos la ecuación Euler-Lagrange

${\displaystyle \frac{\partial F}{\partial y}-\frac{d}{dx}\left(\frac{\partial F}{\partial \dot{y}}\right)=0}$

El resultado es

${\displaystyle \begin{array}{l}\frac{\partial F}{\partial \dot{y}}=\frac{\lambda \dot{y}}{\sqrt{1+{\dot{y}}^2}}\frac{\partial F}{\partial y}=1\\ \frac{d}{dx}\left(\frac{\lambda \dot{y}}{\sqrt{1+{\dot{y}}^2}}\right)=1\\ \lambda \frac{\dot{y}}{\sqrt{1+{\dot{y}}^2}}=x+C_1\end{array}}$

La solución es

${\displaystyle \begin{array}{l}\frac{dy}{dx}=\frac{x+C_1}{\sqrt{{\lambda }^2-{\left(x+C_1\right)}^2}}\\ y+C_2={\displaystyle \int \frac{x+C_1}{\sqrt{{\lambda }^2-{\left(x+C_1\right)}^2}}dx}\\ y+C_2=-\sqrt{{\lambda }^2-{\left(x+C_1\right)}^2}\\ {\left(x+C_1\right)}^2+{\left(y+C_2\right)}^2={\lambda }^2\end{array}}$

Se calculan las constantes C₁ y C₂ sabiendo que la circunferencia pasa por los puntos A(-a,0) y B(a,0)

${\displaystyle \begin{array}{l}{\left(-a+C_1\right)}^2+C_2^2={\lambda }^2\\ {\left(a+C_1\right)}^2+C_2^2={\lambda }^2\end{array}\}{C}_1=0C_2=\sqrt{{\lambda }^2-a^2}}$

Calculamos el parámetro λ sabiendo que la longitud de la curva y=y(x) es l

${\displaystyle \begin{array}{l}y=\sqrt{{\lambda }^2-x^2}-\sqrt{{\lambda }^2-a^2}\\ \frac{dy}{dx}=-\frac{x}{\sqrt{{\lambda }^2-x^2}}\\ l={\displaystyle \underset{-a}{\overset{a}{\int }}\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx}=\lambda {\displaystyle \underset{-a}{\overset{a}{\int }}\sqrt{\frac{1}{\sqrt{{\lambda }^2-x^2}}}}dx={\lambda \arcsin \left(\frac{x}{\lambda }\right)|}_{-a}^a=2\lambda \arcsin \left(\frac{a}{\lambda }\right)\\ \frac{a}{\lambda }=\sin \left(\frac{l}{2\lambda }\right)\end{array}}$

Dado a y l, se resuelve esta última ecuación trascendente y se calcula λ.

a=1;
L=2.5; %longitud

f=@(x) sin(L./(2*x))-a./x;
lambda=fzero(f,1);
c2=sqrt(lambda^2-a^2);
%circunferencia
x1=@(th) lambda*cos(th);
y1=@(th) -c2+lambda*sin(th);
hold on
fplot(x1,y1,[0,2*pi])
%centro de la circunferencia
line([-0.1,0.1],[-c2,-c2], 'color','k');
line([0,0],[-c2+0.1,-c2-0.1], 'color','k');
%puntos (-a,0) (a,0)
plot(-1,0,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
plot(1,0,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
%área
ang=atan(c2/a);
phi=ang:pi/180:pi-ang;
xArea=x1(phi);
yArea=y1(phi);
fill(xArea,yArea,'y')
hold off
grid on
axis equal
ylim([-1,1])
xlabel('x')
ylabel('y')
title('problema de Dido')

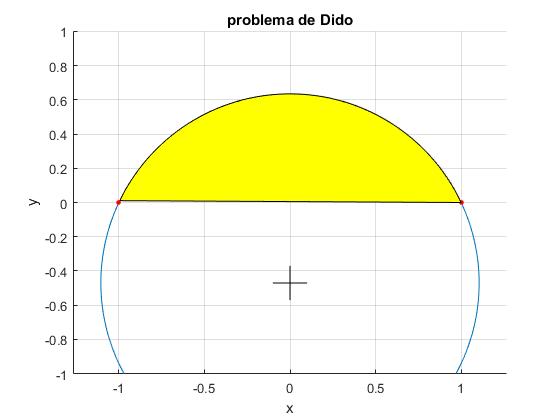
Mostramos el área en color amarillo, el centro (0,-C₂) y radio λ de la circunferencia son

>> c2
c2 =    0.4704
>> lambda
lambda =    1.1051

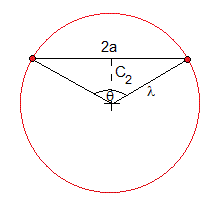
Calculamos la longitud de la circunferencia con los datos del centro C₂ y del radio λ. Como vemos en la figura

${\displaystyle \tan \left(\frac{\theta }{2}\right)=\frac{a}{C_2}}$

Comprobamos que la longitud del arco de circunferencia, l=2θ·λ, es

>> 2*lambda*atan(a/c2)
ans =    2.5000

Ejemplo 2. Ecuación de la superficie de un líquido en rotación

En este apartado utilizaremos el cálculo de variaciones para obtener la ecuación de la parábola z=z(r). La diferencia L=E_k-E_p entre la energía cinética y potencial deberá ser mínima con la condición de que el volumen de líquido permanezca constante.

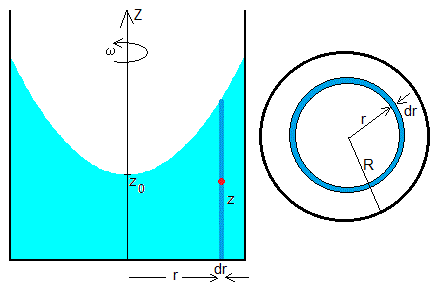
Energía potencial

Consideremos una capa cilíndrica de de radio r, espesor dr y altura z tal como se muestra en la figura. La masa del líquido contenido en esta capa es ρ(2πr·dr·z), el centro de masa, señalado por un punto de color rojo, está a una altura z/2. La energía potencial de esta capa cilíndrica es ρ(2πr·dr·z)z/2. Siendo ρ la densidad del líquido y g la aceleración de la gravedad. La energía potencial del líquido contenido en el cubo cuando está girando alrededor de su eje con velocidad angular constante ω es

${\displaystyle E_p={\displaystyle \underset{0}{\overset{R}{\int }}\rho g\left(2\pi r·dr·z\right)\frac{z}{2}}=\pi \rho g{\displaystyle \underset{0}{\overset{R}{\int }}{z}^{2}r·dr}}$

Energía cinética

La fórmula de la energía cinética de un cuerpo rígido en rotación es

${\displaystyle E_k=\frac{1}{2}I{\omega }^2}$

El momento de inercia respecto del eje de rotación, de una capa cilíndrica de radio r, anchura dr y altura z, es, \rho \left(2\pi r·dr·z\right)r^2. La energía cinética del líquido contenido en el cubo es

${\displaystyle E_k=\frac{1}{2}\left\{{\displaystyle \underset{0}{\overset{R}{\int }}\rho \left(2\pi r·dr·z\right)r^2}\right\}{\omega }^2=\rho {\omega }^2\pi {\displaystyle \underset{0}{\overset{R}{\int }}z{r}^{3}dr}}$

Volumen de líquido en el cubo

El volumen de líquido es πR²h cuando el cubo está en reposo, cuando gira el volumen es

${\displaystyle V={\displaystyle \underset{0}{\overset{R}{\int }}2\pi r·dr·z=2\pi }{\displaystyle \underset{0}{\overset{R}{\int }}zr·dr}}$

Extremo condicionado

Tenemos un problema de extremo condicionado, hallar el extremo de la funcional L=E_k-E_p

${\displaystyle L(z)=\pi {\displaystyle \underset{0}{\overset{R}{\int }}\left(\rho {\omega }^{2}z{r}^3-\rho g{z}^{2}r\right)dr}}$

sujeto a la condición de que el volumen permanezca constante

${\displaystyle V(z)=\pi {\displaystyle \underset{0}{\overset{R}{\int }}\left(2zr\right)}dr}$

Formamos la función

${\displaystyle F(r,z,\dot{z})=L+\lambda V=\pi \left(\rho {\omega }^{2}z{r}^3-\rho g{z}^{2}r\right)+\lambda \pi \left(2zr\right)}$

donde λ es un parámetro que determinaremos más adelante. Aplicamos la ecuación de Euler-Lagrange

${\displaystyle \frac{\partial F}{\partial z}-\frac{d}{dr}\left(\frac{\partial F}{\partial \dot{z}}\right)=0}$

Dado que la función F no depende de la derivada dz/dr, el segundo término es nulo. Nos queda una ecuación muy sencilla ∂F/∂z=0

${\displaystyle \begin{array}{l}\rho {\omega }^2{r}^3-2\rho gzr+2\lambda r=0\\ z=\frac{{\omega }^2}{2g}{r}^2+\frac{\lambda }{\rho g}\end{array}}$

El parámetro desconocido λ se determina sabiendo que el volumen de agua permanece constante, πR²h

${\displaystyle \begin{array}{l}\pi R^{2}h=\pi {\displaystyle \underset{0}{\overset{R}{\int }}\left(2zr\right)}dr\\ R^{2}h=2{\displaystyle \underset{0}{\overset{R}{\int }}\left(\frac{{\omega }^2}{2g}{r}^2+\frac{\lambda }{\rho g}\right)}r·dr\\ R^{2}h=\frac{{\omega }^2}{g}\frac{R^4}{4}+\frac{\lambda }{\rho g}{R}^2\\ \lambda =\rho gh-\rho \frac{{\omega }^2{R}^2}{4}\end{array}}$

Ecuación de la parábola

Finalmente, la ecuación de la superficie del líquido es la de un paraboloide de revolución cuyo eje es el del cilindro. La ecuación de la parábola que genera dicha superficie es

${\displaystyle z=\frac{{\omega }^2}{2g}{r}^2+h-\frac{{\omega }^2{R}^2}{4g}}$

El vértice de la parábola, z₀=h-ω²R²/(4g) se hace cero para una velocidad angular máxima, ω_m

${\displaystyle \frac{{\omega }_m^2}{4g}{R}^2=h}$

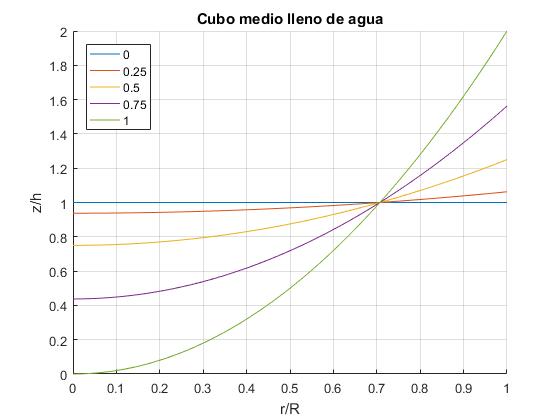
Para esta velocidad la altura z de la capa de fluido más externa, en contacto con las paredes del recipiente, r=R, vale z=2h. El agua empieza a derramarse por el borde del cubo medio lleno de agua. La altura del cubo es 2h

Cuando, $r=\sqrt{2}R$, z=h, independientemente de la velocidad angular ω

La ecuación de la parábola se puede escribir de forma alternativa

${\displaystyle \frac{z}{h}=1-{\left(\frac{\omega }{{\omega }_m}\right)}^2\left(1-2{\left(\frac{r}{R}\right)}^2\right)}$

Representación z/h en términos de r/R, para varios valores de ω/ω_m. Como la parábola es simétrica respecto del eje de rotación, solamente representamos la mitad derecha

hold on
for w=[0,0.25,0.5,0.75,1]
    f=@(x) 1-w^2*(1-2*x.^2);
    fplot(f,[0,1], 'displayName',num2str(w))
end
grid on
legend('-DynamicLegend','location','northwest')
xlabel('r/R')
ylabel('z/h')
title('Cubo medio lleno de agua')

Ejemplo 3

Hallar la curva y=y(x), z=z(x) en la que la funcional

${\displaystyle I(x,y,z)={\displaystyle \underset{0}{\overset{1}{\int }}\left({\dot{y}}^2+{\dot{z}}^2-4x\dot{z}-4z\right)dx}}$

alcanza su valor extremo, con las condiciones de que la funcional

${\displaystyle K(x,y,z)={\displaystyle \underset{0}{\overset{1}{\int }}\left({\dot{y}}^2-x\dot{y}-{\dot{z}}^2\right)dx}=2}$

y en los extremos y(0)=0, y(1)=1, z(0)=0, z(1)=1

Existe un parámetro λ, tal que la curva y=y(x), z=z(x) hace que el funcional

${\displaystyle L(y)={\displaystyle \underset{0}{\overset{1}{\int }}\left({\dot{y}}^2+{\dot{z}}^2-4x\dot{z}-4z+\lambda \left({\dot{y}}^2-x\dot{y}-{\dot{z}}^2\right)\right)dx}}$

alcance su extremo. La ecuación de Euler-Lagrange se escribe ahora para dos variables y, z

${\displaystyle \begin{array}{l}F(x,y,\dot{y},z,\dot{z})=f(x,y,\dot{y},z,\dot{z})+\lambda g(x,y,\dot{y},z,\dot{z})\\ \{\begin{array}{l}\frac{\partial F}{\partial y}-\frac{d}{dx}\left(\frac{\partial F}{\partial \dot{y}}\right)=0\\ \frac{\partial F}{\partial z}-\frac{d}{dx}\left(\frac{\partial F}{\partial \dot{z}}\right)=0\end{array}\end{array}}$

lo que resulta

${\displaystyle \{\begin{array}{l}-\frac{d}{dx}\left(2\dot{y}+2\lambda \dot{y}-\lambda x\right)=0\\ -4-\frac{d}{dx}\left(2\dot{z}-4x-2\lambda \dot{z}\right)=0\end{array}}$

La solución es

${\displaystyle \begin{array}{l}\{\begin{array}{l}\left(2+2\lambda \right)\frac{dy}{dx}-\lambda x=C_1\\ \left(2-2\lambda \right)\frac{dz}{dx}-4x=-4x+C_3\end{array}\\ \{\begin{array}{l}y=\frac{\lambda x^2+2C_{1}x}{4(1+\lambda )}+C_2\\ z=\frac{C_{3}x}{2(1-\lambda )}+C_4\end{array}\end{array}}$

Calculamos las constantes C₁, C₂, C₃ y C₄, a partir de las condiciones en los extremos

${\displaystyle C_1=\frac{3\lambda +4}{2}{C}_2=0C_3=2(1-\lambda )C_4=0}$

La curva buscada y=y(x), z=z(x) en función del parámetro λ es

${\displaystyle \{\begin{array}{l}y=\frac{\lambda x^2+(3\lambda +4)x}{4(1+\lambda )}\\ z=x\end{array}}$

Calculamos el valor del parámetro λ a partir de la condición de que el funcional K(x,y,z) valga 2

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{1}{\int }}\left({\left(\frac{dy}{dx}\right)}^2-x\frac{dy}{dx}-{\left(\frac{dz}{dx}\right)}^2\right)dx}=2\\ {\displaystyle \underset{0}{\overset{1}{\int }}\left\{{\left(\frac{2\lambda x+3\lambda +4}{4(1+\lambda )}\right)}^2+\frac{2\lambda x+3\lambda +4}{4(1+\lambda )}x-1\right\}dx}=2\end{array}}$

La integral es sencilla pero requiere muchas operaciones algebraicas, por lo que utilizamos MATLAB para realizar esta tarea. La integral definida que se iguala a 2 da como resultado una ecuación de segundo grado en λ (en el código k es λ), que tiene dos raíces reales λ₁=-12/11 y λ₂=-10/11. Calculamos el funcional I(x,y,z) y nos da como resultado 1 para la primera raíz, y 1/12 para la segunda

>> syms x k;
>> yp=(2*k*x+3*k+4)/(4+4*k);
>> z=int(yp^2-x*yp-1,x,0,1)
z =1/(48*(k + 1)^2) - 25/48
>> s=solve(z-2)
 s = -12/11
 -10/11
>> y1=subs(yp,k,s(1))
 y1 =6*x - 2
>> y2=subs(yp,k,s(2))
y2 =7/2 - 5*x
>> int(y1^2 + 1 - 4*x - 4*x,x,0,1)
 ans =1
>> int(y2^2 + 1 - 4*x - 4*x,x,0,1)
 ans =1/12

La curva buscada y=y(x), z=z(x) para cada una de las raíces es

${\displaystyle \begin{array}{l}{\lambda }_1=-\frac{12}{11}\{\begin{array}{l}y=3x^2-2x\\ z=x\end{array}\\ {\lambda }_2=-\frac{10}{11}\{\begin{array}{l}y=\frac{1}{2}\left(-5x^2+7x\right)\\ z=x\end{array}\end{array}}$

Integrando en el código las derivadas y1=6x-2 e y2=7/2-5x, obtenemos los resultados anteriores

El cálculo de variaciones en otras páginas del Curso de Física

Alcance máximo en un plano inclinado

Viaje en tren en un tiempo mínimo

Función de distribución de Boltzmann (II)

Distancia más corta, superficie mínima, forma de un cuerpo

La braquistócrona

El principio de Fermat

La catenaria

El viaje más rápido a través de un túnel por el interior de la Tierra

Braquistócrona en el campo gravitatorio no uniforme de la Tierra

Película jabonosa entre dos aros

La forma que adopta una cuerda bajo la acción de su peso y de la tensión superficial

El perfil de una gota de rocío

Referencias

M. L. Krasnov, G. I. Makarenko, A. I. Kiseliov. Cálculo Variacional (ejemplos y problemas). Editorial Mir (1992)