Escalón lineal y barrera de potencial de forma triangular

Escalón de potencial

En este apartado, resolveremos la ecuación de Schrödinger unidimensional e independiente del tiempo

$\frac{- ℏ^{2}}{2 m} \frac{d^{2} Ψ}{d x^{2}} + V (x) Ψ = E Ψ$

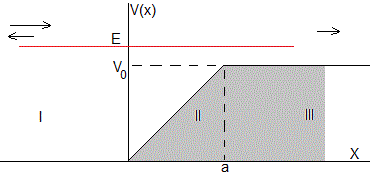
en el potencial

$V (x) = {\begin{cases} 0, x < 0 \\ V_{0} \frac{x}{a}, 0 \leq x < a \\ V_{0}, x \geq a \end{cases}$

Ya se ha estudiado la solución de la ecuación de Schrödinger para E>V₀ en las regiones I y III

$\begin{array}{l} \frac{d^{2} ψ_{I} (x)}{d x^{2}} + \frac{2 m}{ℏ^{2}} E \cdot ψ_{I} (x) = 0, ψ_{I} (x) = A \exp (i k x) + B \exp (- i k x), k^{2} = \frac{2 m}{ℏ^{2}} E \\ \frac{d^{2} ψ_{I I I} (x)}{d x^{2}} + \frac{2 m}{ℏ^{2}} (E - V_{0}) \cdot ψ_{I I I} (x) = 0, ψ_{I I I} (x) = C \exp (i q x) + D \exp (- i q x), q^{2} = \frac{2 m}{ℏ^{2}} (E - V_{0}) \end{array}$

No hay partículas que viajen de derecha a izquierda por lo que el coeficiente D=0. En la región II la solución de la ecuación de Schrödinger es más complicada

$\begin{array}{l} \frac{d^{2} ψ_{I I} (x)}{d x^{2}} + \frac{2 m}{ℏ^{2}} (E - V_{0} \frac{x}{a}) \cdot ψ_{I I} (x) = 0 \\ \frac{d^{2} ψ_{I I} (x)}{d x^{2}} - ((k^{2} - q^{2}) \frac{x}{a} - k^{2}) \cdot ψ_{I I} (x) = 0 \end{array}$

Hacemos el cambio de variable z=αx+β, dz=α·dx, de modo que la ecuación diferencial se transforme

$\frac{d^{2} ψ_{I I} (z)}{d z^{2}} - z \cdot ψ_{I I} (z) = 0, ψ_{I I} (z) = E \cdot Ai (z) + F \cdot Bi (z)$

cuya solución es una combinación lineal de las funciones de Airy, Ai(x) y Bi(x). El resultado es

$\begin{array}{l} z = \frac{1}{α^{2}} ((k^{2} - q^{2}) \frac{x}{a} - k^{2}) = α x + β, {\begin{cases} α^{3} = \frac{k^{2} - q^{2}}{a} \\ β = - \frac{k^{2}}{α^{2}} \end{cases} \\ z = {(\frac{2 m}{ℏ^{2}} a^{2} V_{0})}^{1 / 3} (\frac{x}{a} - \frac{E}{V_{0}}) = r (\frac{x}{a} - \frac{E}{V_{0}}) \end{array}$

siendo r un número adimensional

Continuidad

La función de onda y su derivada primera son continuas en x=0 y en x=a que se corresponden con los valores z₀ y z_a de la variable z.

$\begin{array}{l} z_{0} = - r \frac{E}{V_{0}} \\ z_{a} = r (1 - \frac{E}{V_{0}}) \end{array}$

Condiciones de continuidad en x=0

$\begin{array}{l} ψ_{I} (0) = ψ_{I I} (z_{0}) \\ {\frac{d ψ_{I} (x)}{d x} |}_{x = 0} = {\frac{d ψ_{I I} (x)}{d x} |}_{x = 0} \end{array}$

La segunda condición se expresa en términos de la variable z

$\begin{array}{l} \frac{d ψ_{I I} (x)}{d x} = \frac{d ψ_{I I} (z)}{d z} \frac{d z}{d x} = \frac{r}{a} \frac{d ψ_{I I} (z)}{d z} \\ {\frac{d ψ_{I} (x)}{d x} |}_{x = 0} = \frac{r}{a} {\frac{d ψ_{I I} (z)}{d z} |}_{z = z_{0}} \end{array}$

La continuidad en x=0, es

$x = 0 {\begin{cases} A + B = E \cdot Ai (z_{0}) + F \cdot Bi (z_{0}) \\ i k a (A - B) = r (E \cdot Ai' (z_{0}) + F \cdot Bi' (z_{0})) \end{cases}$

El símbolo ' significa la derivada de las función de Airy Ai(z) o Bi(z) respecto de la variable z. Esta derivada se evalúa en z=z₀

Condiciones de continuidad en x=a

Del mismo modo

$x = a {\begin{cases} E \cdot Ai (z_{a}) + F \cdot Bi (z_{a}) = C \exp (i q a) \\ r (E \cdot Ai' (z_{a}) + F \cdot Bi' (z_{a})) = i q a C \exp (i q a) \end{cases}$

Coeficiente de transmisión T

El sistema de cuatro ecuaciones con cuatro incógnitas, B, C, E y F se expresa en forma matricial

$\begin{array}{l} {(\begin{matrix} e^{i k x} & e^{- i k x} \\ i k a e^{i k x} & - i k a e^{- i k x} \end{matrix})}_{0} (\begin{matrix} A \\ B \end{matrix}) = {(\begin{matrix} Ai (x) & Bi (x) \\ r \cdot Ai' (x) & r \cdot Bi' (x) \end{matrix})}_{z_{0}} (\begin{matrix} E \\ F \end{matrix}) \\ {(\begin{matrix} Ai (x) & Bi (x) \\ r \cdot Ai' (x) & r \cdot Bi' (x) \end{matrix})}_{z_{a}} (\begin{matrix} E \\ F \end{matrix}) = {(\begin{matrix} e^{i q x} & e^{- i q x} \\ i q a e^{i q x} & - i q a e^{- i q x} \end{matrix})}_{a} (\begin{matrix} C \\ D \end{matrix}) \end{array}$

Despejamos el vector (C; D) en términos del vector (A; B)

$(\begin{matrix} C \\ D \end{matrix}) = {Q^{- 1} (a) A (z_{a})} {A^{- 1} (z_{0}) K (0)} (\begin{matrix} A \\ B \end{matrix})$

Matrices inversas

$\begin{array}{l} {(\begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix})}^{- 1} = \frac{1}{| \begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix} |} (\begin{matrix} a_{22} & - a_{12} \\ - a_{21} & a_{11} \end{matrix}) \\ {(\begin{matrix} e^{i k x} & e^{- i k x} \\ i k a e^{i k x} & - i k a e^{- i k x} \end{matrix})}^{- 1} = \frac{1}{2} (\begin{matrix} e^{- i k x} & \frac{e^{- i k x}}{i k a} \\ e^{i k x} & - \frac{e^{i k x}}{i k a} \end{matrix}) \\ {(\begin{matrix} Ai (x) & Bi (x) \\ r \cdot Ai' (x) & r \cdot Bi' (x) \end{matrix})}^{- 1} = \frac{π}{r} (\begin{matrix} r \cdot Bi' (x) & -Bi (x) \\ - r \cdot Ai' (x) & Ai (x) \end{matrix}) \end{array}$

Hemos utilizado la propiedad de las funciones de Airy

$Ai (x) \cdot Bi' (x) - Bi (x) Ai' (x) = \frac{1}{π}$

El resultado del producto de las cuatro matrices es una matriz T de 2×2. Asignamos a A=1 y D=0

$\begin{array}{l} (\begin{matrix} C \\ 0 \end{matrix}) = (\begin{matrix} t_{11} & t_{12} \\ t_{21} & t_{22} \end{matrix}) (\begin{matrix} A \\ B \end{matrix}), {\begin{cases} C = t_{11} A + t_{12} B \\ 0 = t_{21} A + t_{22} B \end{cases} \\ B = - \frac{t_{21}}{t_{22}} A, C = (t_{11} - \frac{t_{21} t_{12}}{t_{22}}) A \end{array}$

Se definen los coeficiente de reflexión R y transmisión T

$R = \frac{{| B |}^{2}}{{| A |}^{2}}, T = \frac{v'}{v} \frac{{| C |}^{2}}{{| A |}^{2}} = \frac{q}{k} \frac{{| C |}^{2}}{{| A |}^{2}}$

Hemos calculado el coeficiente de transmisión para un escalón de potencial de altura V₀

$T = \frac{4 \sqrt{E} \sqrt{E - V_{0}}}{{(\sqrt{E} + \sqrt{E - V_{0}})}^{2}}$

Establecemos un sistema de unidades en el que ℏ=m=1. Representamos los dos coeficientes de transmisión para V₀=1.5

a=1; %anchura escalón
V0=1.5; %altura
ee=linspace(V0,4*V0,200);
T=zeros(1,length(ee));
R=zeros(1,length(ee));
T1=zeros(1,length(ee));
i=1;
rr=(2*a^2*V0)^(1/3); %constante
for e=ee
    q=sqrt(2*(e-V0));
    k=sqrt(2*e);
    z0=-rr*(e/V0);
    za=rr*(1-e/V0);
    f=@(z,r) [exp(1i*r*z), exp(-1i*r*z); 1i*r*a*exp(1i*r*z), 
-1i*r*a*exp(-1i*r*z)]; 
    g=@(z,r) [exp(-1i*r*z), exp(-1i*r*z)/(1i*r*a); exp(1i*r*z), 
-exp(1i*r*z)/(1i*r*a)]/2;  %inversa
    h=@(z) [airy(0,z),airy(2,z); rr*airy(1,z),rr*airy(3,z)];
    l=@(z) [rr*airy(3,z),-airy(2,z); -rr*airy(1,z),airy(0,z)]*(pi/rr);
    M=(g(a,q)*h(za))*(l(z0)*f(0,k));
    B=-M(2,1)/M(2,2);
    C=M(1,1)+M(1,2)*B;
    T(i)=abs(C)^2*q/k;
    R(i)=abs(B)^2;
    T1(i)=4*sqrt(e)*sqrt(e-V0)/(sqrt(e)+sqrt(e-V0))^2;
    i=i+1;
end
hold on
plot(ee,T);
plot(ee,T1);
hold off
grid on
ylim([0.5,1.05])
legend('lineal','rectangular','location','best')
xlabel('E')
ylabel('T')
title('Coeficiente de transmisión')

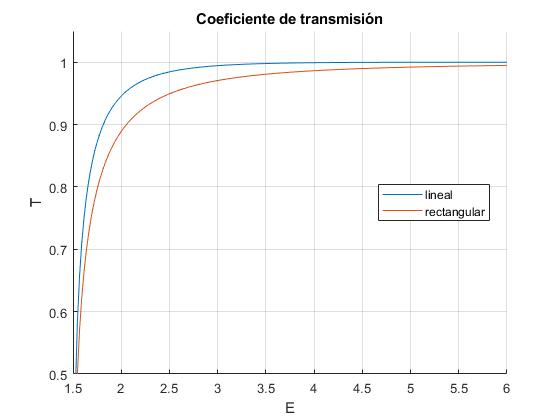
La barrera triangular produce un coeficiente de transmisión mayor que la rectangular de la misma altura V₀

Comprobamos que la suma de los coeficientes R y T es la unidad

>> R(5:11)+T(5:11)
ans =    1.0000    1.0000    1.0000    1.0000    1.0000    1.0000    1.0000

Barrera de potencial de forma triangular

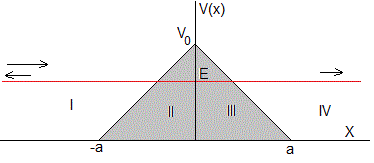
En este apartado, resolveremos la ecuación de Schrödinger unidimensional e independiente del tiempo en el potencial

$V (x) = {\begin{cases} 0, x < - a \\ V_{0} \frac{x}{a} + V_{0}, - a \leq x < 0 \\ - V_{0} \frac{x}{a} + V_{0}, 0 \leq x \leq a \\ 0, x > a \end{cases}$

Ya se ha estudiado la solución de la ecuación de Schrödinger para E<V₀ en las regiones I y IV

$\begin{array}{l} \frac{d^{2} ψ_{I} (x)}{d x^{2}} + \frac{2 m}{ℏ^{2}} E \cdot ψ_{I} (x) = 0, ψ_{I} (x) = A \exp (i k x) + B \exp (- i k x), k^{2} = \frac{2 m}{ℏ^{2}} E \\ \frac{d^{2} ψ_{I V} (x)}{d x^{2}} - \frac{2 m}{ℏ^{2}} (V) E \cdot ψ_{I V} (x) = 0, ψ_{I V} (x) = C \exp (i k x) + D \exp (- i k x) \end{array}$

No hay partículas que viajen de derecha a izquierda por lo que el coeficiente D=0. En las regiones II y III la solución de la ecuación de Schrödinger es más complicada

$\begin{array}{l} \frac{d^{2} ψ_{I I} (x)}{d x^{2}} - \frac{2 m}{ℏ^{2}} (V_{0} + V_{0} \frac{x}{a} - E) \cdot ψ_{I I} (x) = 0 \\ \frac{d^{2} ψ_{I I} (x)}{d x^{2}} - (q^{2} (1 + \frac{x}{a}) - k^{2}) \cdot ψ_{I I} (x) = 0, q^{2} = \frac{2 m}{ℏ^{2}} V_{0} \end{array}$

En la región II, hacemos el cambio de variable z=αx+β, dz=α·dx, de modo que la ecuación diferencial se transforme

$\frac{d^{2} ψ_{I I} (z)}{d z^{2}} - z \cdot ψ_{I I} (z) = 0, ψ_{I I} (z) = E \cdot Ai (z) + F \cdot Bi (z)$

cuya solución es una combinación lineal de las funciones de Airy, Ai(x) y Bi(x). El resultado es

$\begin{array}{l} z = \frac{1}{α^{2}} (q^{2} \frac{x}{a} + q^{2} - k^{2}) = α x + β, {\begin{cases} α^{3} = \frac{q^{2}}{a} \\ β = \frac{q^{2} - k^{2}}{α^{2}} \end{cases} \\ z = {(\frac{2 m}{ℏ^{2}} a^{2} V_{0})}^{1 / 3} (\frac{x}{a} + \frac{V_{0} - E}{V_{0}}) = r (\frac{x}{a} + \frac{V_{0} - E}{V_{0}}) \end{array}$

siendo r un número adimensional. En la región III la solución de la ecuación de Schrödinger es similar

$\begin{array}{l} \frac{d^{2} ψ_{I I I} (x)}{d x^{2}} - \frac{2 m}{ℏ^{2}} (V_{0} - V_{0} \frac{x}{a} - E) \cdot ψ_{I I I} (x) = 0 \\ \frac{d^{2} ψ_{I I I} (x)}{d x^{2}} - (q^{2} (1 - \frac{x}{a}) - k^{2}) \cdot ψ_{I I I} (x) = 0 \end{array}$

Hacemos el cambio de variable y=αx+β, dy=α·dx, de modo que la ecuación diferencial se transforme

$\frac{d^{2} ψ_{I I I} (y)}{d y^{2}} - y \cdot ψ_{I I I} (y) = 0, ψ_{I I I} (y) = M \cdot Ai (y) + N ·Bi (y)$

cuya solución es una combinación lineal de las funciones de Airy, Ai(x) y Bi(x). El resultado es similar

$\begin{array}{l} y = \frac{1}{α^{2}} (- q^{2} \frac{x}{a} + q^{2} - k^{2}) = α x + β, {\begin{cases} α^{3} = - \frac{q^{2}}{a} \\ β = \frac{q^{2} - k^{2}}{α^{2}} \end{cases} \\ y = r (- \frac{x}{a} + \frac{V_{0} - E}{V_{0}}) \end{array}$

Continuidad

La función de onda y su derivada primera son continuas en x=-a, x=0 y en x=a. Los valores de las variables z e y en estos puntos son

$\begin{array}{l} x = - a, z_{a} = - r \frac{E}{V_{0}} \\ x = a, y_{a} = z_{a} \\ x = 0, y_{0} = z_{0} = r (\frac{V_{0} - E}{V_{0}}) \end{array}$

Condiciones de continuidad en x=-a

$\begin{array}{l} ψ_{I} (- a) = ψ_{I I} (z_{a}) \\ {\frac{d ψ_{I} (x)}{d x} |}_{x = - a} = {\frac{d ψ_{I I} (x)}{d x} |}_{x = - a} \end{array}$

La segunda condición (continuidad de la derivada primera) se expresa en términos de la variable z

$\begin{array}{l} \frac{d ψ_{I I} (x)}{d x} = \frac{d ψ_{I I} (z)}{d z} \frac{d z}{d x} = \frac{r}{a} \frac{d ψ_{I I} (z)}{d z} \\ {\frac{d ψ_{I} (x)}{d x} |}_{x = - a} = \frac{r}{a} {\frac{d ψ_{I I} (z)}{d z} |}_{z = z_{a}} \end{array}$

La continuidad en x=-a, es

$x = - a {\begin{cases} A \exp (- i k a) + B \exp (i k a) = E \cdot Ai (z_{a}) + F \cdot Bi (z_{a}) \\ i k a (A \exp (- i k a) - B \exp (i k a)) = r (E \cdot Ai' (z_{a}) + F \cdot Bi' (z_{a})) \end{cases}$

Condiciones de continuidad en x=0

La segunda condición se expresa en términos de la variable y

$\begin{array}{l} \frac{d ψ_{I I I} (x)}{d x} = \frac{d ψ_{I I I} (y)}{d y} \frac{d y}{d x} = - \frac{r}{a} \frac{d ψ_{I I I} (y)}{d y} \\ {\frac{r}{a} \frac{d ψ_{I I} (z)}{d z} |}_{z = z_{0}} = - \frac{r}{a} {\frac{d ψ_{I I I} (y)}{d y} |}_{y = z_{0}} \end{array}$

La continuidad en x=0, es

$x = 0 {\begin{cases} E \cdot Ai (z_{0}) + F \cdot Bi (z_{0}) = M \cdot Ai (z_{0}) + N \cdot Bi (z_{0}) \\ r (E \cdot Ai' (z_{0}) + F \cdot Bi' (z_{0})) = - r (M \cdot Ai' (z_{0}) + N \cdot Bi' (z_{0})) \end{cases}$

Condiciones de continuidad en x=a

$x = a {\begin{cases} M \cdot Ai (z_{a}) + N \cdot Bi (z_{a}) = C \exp (i k a) \\ - r (M \cdot Ai' (z_{a}) + N \cdot Bi' (z_{a})) = i k a C \exp (i k a) \end{cases}$

Coeficiente de transmisión T

El sistema de seis ecuaciones con seis incógnitas, B, C, E, F, M, N se expresa en forma matricial

$\begin{array}{l} {(\begin{matrix} e^{i k x} & e^{- i k x} \\ i k a e^{i k x} & - i k a e^{- i k x} \end{matrix})}_{- a} (\begin{matrix} A \\ B \end{matrix}) = {(\begin{matrix} Ai (x) & Bi (x) \\ r \cdot Ai' (x) & r \cdot Bi' (x) \end{matrix})}_{z_{a}} (\begin{matrix} E \\ F \end{matrix}) \\ {(\begin{matrix} Ai (x) & Bi (x) \\ r \cdot Ai' (x) & r \cdot Bi' (x) \end{matrix})}_{z_{0}} (\begin{matrix} E \\ F \end{matrix}) = {(\begin{matrix} Ai (x) & Bi (x) \\ - r \cdot Ai' (x) & - r \cdot Bi' (x) \end{matrix})}_{z_{0}} (\begin{matrix} M \\ N \end{matrix}) \\ {(\begin{matrix} Ai (x) & Bi (x) \\ - r \cdot Ai' (x) & - r \cdot Bi' (x) \end{matrix})}_{z_{a}} (\begin{matrix} M \\ N \end{matrix}) = {(\begin{matrix} e^{i k x} & e^{- i k x} \\ i k a e^{i k x} & - i k a e^{- i k x} \end{matrix})}_{a} (\begin{matrix} C \\ D \end{matrix}) \end{array}$

Despejamos el vector (C; D) en términos del vector (A; B)

$(\begin{matrix} C \\ D \end{matrix}) = {K^{- 1} (a) A_{-} (z_{a})} {A_{-}^{- 1} (z_{0}) A_{+} (z_{0})} {A_{+}^{- 1} (z_{a}) K (- a)} (\begin{matrix} A \\ B \end{matrix})$

Matrices inversas

En el apartado anterior hemos calculado las inversas de dos matrices cuadradas

${(\begin{matrix} Ai (x) & Bi (x) \\ - r \cdot Ai' (x) & - r \cdot Bi' (x) \end{matrix})}^{- 1} = \frac{π}{r} (\begin{matrix} r \cdot Bi' (x) & Bi (x) \\ - r \cdot Ai' (x) & - Ai (x) \end{matrix})$

El resultado del producto de las seis matrices es una matriz T de 2×2. Asignamos a A=1 y D=0

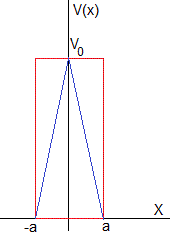
Se definen los coeficiente de reflexión R y transmisión T para la barrera de forma triangular (color azul)

$R = \frac{{| B |}^{2}}{{| A |}^{2}}, T = \frac{{| C |}^{2}}{{| A |}^{2}}$

El coeficiente de transmisión para una barrera de potencial rectangular (color rojo) de altura V₀ y anchura 2a es

$T = \frac{4 E (V_{0} - E)}{4 E (V_{0} - E) + V_{0}^{2} \sinh^{2} (2 q a)}, q = \frac{2 m (V_{0} - E)}{ℏ^{2}}$

Establecemos un sistema de unidades en el que ℏ=m=1. Representamos los dos coeficientes de transmisión para una barrera de altura V₀=10 y de anchura 2a=2·0.25

a=0.25; %la anchura barrera es 2a
V0=10; %altura
ee=linspace(0.1,V0,200);
T=zeros(1,length(ee));
R=zeros(1,length(ee));
T1=zeros(1,length(ee));
i=1;
rr=(2*a^2*V0)^(1/3); %constante
q=sqrt(2*V0);
for e=ee
    k=sqrt(2*e);
    za=rr*(-1+(V0-e)/V0);
    z0=rr*(V0-e)/V0;
    f=@(z,r) [exp(1i*r*z), exp(-1i*r*z); 1i*r*a*exp(1i*r*z), 
-1i*r*a*exp(-1i*r*z)]; 
    g=@(z,r) [exp(-1i*r*z), exp(-1i*r*z)/(1i*r*a); exp(1i*r*z), 
-exp(1i*r*z)/(1i*r*a)]/2;  %inversa
    h1=@(z) [airy(0,z),airy(2,z); rr*airy(1,z),rr*airy(3,z)];
    l1=@(z) [rr*airy(3,z),-airy(2,z); -rr*airy(1,z),airy(0,z)]*(pi/rr);
    h2=@(z) [airy(0,z),airy(2,z); -rr*airy(1,z),-rr*airy(3,z)];
    l2=@(z) [rr*airy(3,z),airy(2,z); -rr*airy(1,z),-airy(0,z)]*(pi/rr);
    M=(g(a,k)*h2(za))*(l2(z0)*h1(z0))*(l1(za)*f(-a,k));
    B=-M(2,1)/M(2,2);
    C=M(1,1)+M(1,2)*B;
    T(i)=abs(C)^2; %barrera triangular
    R(i)=abs(B)^2;
    qq=sqrt(2*(V0-e));
    T1(i)=4*e*(V0-e)/(4*e*(V0-e)+(V0*sinh(qq*2*a))^2); %barrera rectangular
    i=i+1;
end
hold on
plot(ee,T);
plot(ee,T1);
hold off
grid on
legend('triangular','rectangular','location','best')
xlabel('E')
ylabel('T')
title('Coeficiente de transmisión')

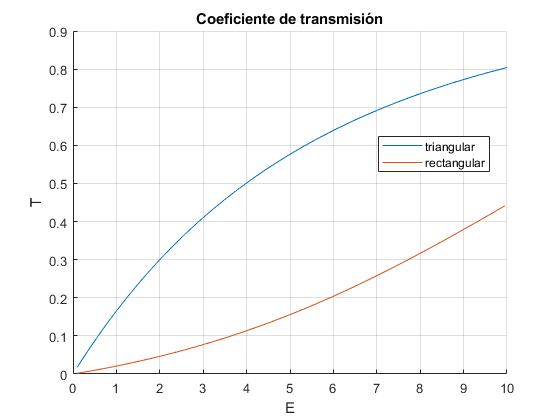
Comprobamos que la suma de los coeficientes R y T es la unidad

>> R(5:11)+T(5:11)
ans =    1.0000    1.0000    1.0000    1.0000    1.0000    1.0000    1.0000

Función de onda

Representamos la función de onda

$\begin{array}{l} ψ_{I} (x) = A \exp (i k x) + B \exp (- i k x), - \infty < x < a, k^{2} = \frac{2 m}{ℏ^{2}} E, \\ ψ_{I I} (z) = E \cdot Ai (z) + F \cdot Bi (z), - a \leq x < 0, z = {(\frac{2 m}{ℏ^{2}} a^{2} V_{0})}^{1 / 3} (\frac{x}{a} + \frac{V_{0} - E}{V_{0}}) \\ ψ_{I I I} (y) = M \cdot Ai (y) + N ·Bi (y), 0 \leq x < a, y = r (- \frac{x}{a} + \frac{V_{0} - E}{V_{0}}) \\ ψ_{I V} (x) = C \exp (i k x), x \geq a \end{array}$

Para la energía E=2.5. Los datos de la barrera triangular son a=0.25 y la altura V₀=2.5

a=0.25; %la anchura barrera es 2a
V0=10; %altura
rr=(2*a^2*V0)^(1/3); %constante
q=sqrt(2*V0);
e=2.5; %nergía (cambiar)
k=sqrt(2*e);
za=rr*(-1+(V0-e)/V0);
z0=rr*(V0-e)/V0;
f=@(z,r) [exp(1i*r*z), exp(-1i*r*z); 1i*r*a*exp(1i*r*z), -1i*r*a*exp(-1i*r*z)]; 
g=@(z,r) [exp(-1i*r*z), exp(-1i*r*z)/(1i*r*a); exp(1i*r*z),
 -exp(1i*r*z)/(1i*r*a)]/2;  %inversa
h1=@(z) [airy(0,z),airy(2,z); rr*airy(1,z),rr*airy(3,z)];
l1=@(z) [rr*airy(3,z),-airy(2,z); -rr*airy(1,z),airy(0,z)]*(pi/rr);
h2=@(z) [airy(0,z),airy(2,z); -rr*airy(1,z),-rr*airy(3,z)];
l2=@(z) [rr*airy(3,z),airy(2,z); -rr*airy(1,z),-airy(0,z)]*(pi/rr);
S=(g(a,k)*h2(za))*(l2(z0)*h1(z0))*(l1(za)*f(-a,k));
A=1;
B=-S(2,1)/S(2,2);
C=S(1,1)+S(1,2)*B;
R=(l1(za)*f(-a,k))*[A;B];
E=R(1); F=R(2);
R=(l2(za)*f(a,k))*[C;0];
M=R(1); N=R(2);
hold on
line([-a,-a],[-1,-0.5], 'lineStyle','--','color','k')
line([a,a],[-1,-0.5], 'lineStyle','--','color','k')
fplot(@(x) real(A*exp(1i*k*x)+B*exp(-1i*k*x)),[-3,-a]) %incidente + reflejada
%fplot(@(x) real(A*exp(1i*k*x)),[-3,-a]) %incidente
%fplot(@(x) real(B*exp(-1i*k*x)),[-3,-a]) %reflejada
fplot(@(x) real(C*exp(1i*k*x)),[a,3]) %transmitida
fplot(@(x) real(E*airy(0,rr*(x/a+(V0-e)/V0))+
F*airy(2,rr*(x/a+(V0-e)/V0))),[-a,0])
fplot(@(x) real(M*airy(0,rr*(-x/a+(V0-e)/V0))+
N*airy(2,rr*(-x/a+(V0-e)/V0))),[0,a])
hold off
grid on
xlabel('x')
ylabel('\Psi(x)')
title('Función de onda')

Las dos líneas verticales a trazos, marcan las regíones II y III de anchura 2a

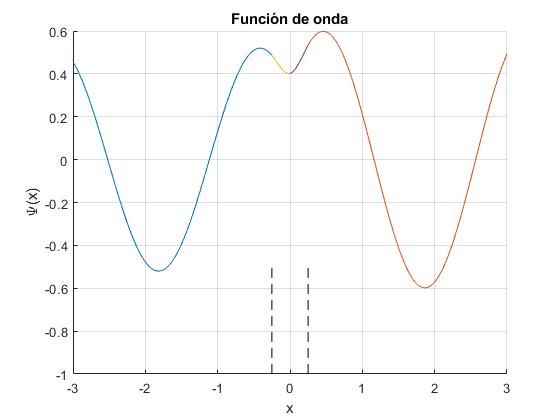
En la región I, se separa la función de onda de las partículas incidentes (en color azul) de las reflejadas (color anaranjado). En la región IV tenemos la función de onda de las partículas transmitidas

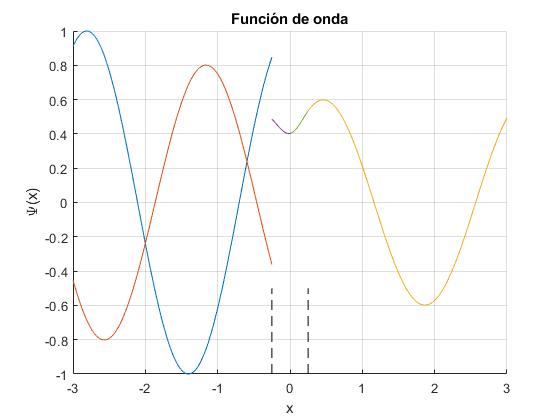
Referencias

R. Delbourgo. On the linear potential hill. Am. J. Phys. 45 (11) November 1977, pp. 1110-1112

I.I. Gol'dma. V.D. Krivchenkov. V.I. Kogan. V.M. Galitskii. Problems In Quantum Mehcanics. D. Ter Haar (Editor). pion-london. Problema 2.7, pág 11, solución, 135-136