Sistema simple

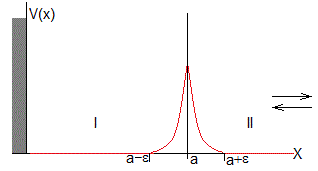
Resolveremos la ecuación de Schrödinger para una barrera de potencial delta de Dirac, centrada en la posición x=a, y una pared de potencial de altura infinita situda en el origen x≤0

${\displaystyle \begin{array}{l}-\frac{{\hslash }^2}{2m}\frac{d^2\psi (x)}{d{x}^2}+V(x)·\psi (x)=E·\psi (x)\\ V(x)=\{\begin{array}{l}\infty ,x\le 0\\ \frac{{\hslash }^2}{2m}\alpha ·\delta (x-a),x>0\end{array}\end{array}}$

Representamos el potencial delta de Dirac por la función que se muestra en la figura, una barrera de anchura 2ε y altura que tiende a infinito, siendo ε→0

• Región I, V(x)=0

${\displaystyle \begin{array}{l}\frac{d^2\psi }{d{x}^2}+\frac{2m}{{\hslash }^2}E·\psi =\mathrm{0,}E<0\\ \frac{d^2\psi }{d{x}^2}-k^2·\psi =\mathrm{0,}{k}^2=-\frac{2m}{{\hslash }^2}E\\ {\psi }_I(x)=A\exp (-kx)+B\exp (kx)\end{array}}$

En la pared de altura infinita Ψ_I(0)=0, por lo que A+B=0. La función de onda es

${\displaystyle {\psi }_I(x)=2iA\sin (kx),0<x<a}$

• Región II, V(x)=0

${\displaystyle \begin{array}{l}\frac{d^2\psi }{d{x}^2}+\frac{2m}{{\hslash }^2}E·\psi =\mathrm{0,}{k}^2=\frac{2m}{{\hslash }^2}E\\ {\psi }_{II}(x)=C\exp (ikx)+D\exp (-ikx),x>a\end{array}}$

D es la amplitud de la función de onda de las partículas incidentes (se mueven de derecha a izquierda) y C de las reflejadas. Se tendrá que cumplir que |D|²=|C|²

En x=a

• La función de onda es continua

${\displaystyle \begin{array}{l}{\psi }_I(a)={\psi }_{II}(a)\\ 2iA\sin (ka)=C\exp (ika)+D\exp (-ika)\end{array}}$

• Pero no lo es su derivada primera. Integramos la ecuación de Schrödinger en el pequeño intervalo de (a-ε, a+ε)

${\displaystyle \begin{array}{l}-\frac{{\hslash }^2}{2m}{\displaystyle \underset{a-\epsilon }{\overset{a+\epsilon }{\int }}\frac{d^2\psi (x)}{d{x}^2}}dx+{\displaystyle \underset{a-\epsilon }{\overset{a+\epsilon }{\int }}\alpha \frac{{\hslash }^2}{2m}\delta (x-a)·\psi (x)·dx}=E·{\displaystyle \underset{a-\epsilon }{\overset{a+\epsilon }{\int }}\psi (x)·dx}\\ -\frac{{\hslash }^2}{2m}\underset{\epsilon \to 0}{\lim }\left({\frac{d{\psi }_{II}(x)}{dx}|}_{a+\epsilon }-{\frac{d{\psi }_I(x)}{dx}|}_{a-\epsilon }\right)-\alpha \frac{{\hslash }^2}{2m}{\psi }_I(a)=0\\ \underset{\epsilon \to 0}{-\lim }\left({ikC\exp (ikx)-ikD\exp (-ikx)|}_{a+\epsilon }{-\left(2ikA\cos (kx)\right)|}_{a-\epsilon }\right)+\alpha \left(2iA\sin (ka)\right)=0\\ -\underset{\epsilon \to 0}{\lim }\left(\left(ikC\exp \left(ik(a+\epsilon )\right)-ikD\exp \left(-ik(a+\epsilon )\right)\right)-\left(2ikA\cos \left(k(a-\epsilon )\right)\right)\right)+\alpha \left(2iA\sin (ka)\right)=0\\ -kC\exp \left(ika\right)+kD\exp \left(-ika\right)+2kA\cos \left(ka\right)+2\alpha A\sin (ka)=0\end{array}}$

Vamos a calcular el cuadrado del módulo de la amplitud |A|² en función de el coeficiente D, resolviendo el sistema de dos ecuaciones

${\displaystyle \begin{array}{l}\{\begin{array}{l}2iA\sin (ka)=C\exp (ika)+D\exp (-ika)\\ 2kA\cos \left(ka\right)+2\alpha A\sin (ka)=kC\exp \left(ika\right)-kD\exp \left(-ika\right)\end{array}\\ A=D\frac{k\left(\cos (ka)-i\cos (ka)\right)}{-k\cos \left(ka\right)-\alpha \sin (ka)+ik\sin (ka)}\\ A=Dk\frac{\left(\cos (ka)-i\cos (ka)\right)\left(-k\cos \left(ka\right)-\alpha \sin (ka)-ik\sin (ka)\right)}{\left(-k\cos \left(ka\right)-\alpha \sin (ka)+ik\sin (ka)\right)\left(-k\cos \left(ka\right)-\alpha \sin (ka)-ik\sin (ka)\right)}=\\ A=-Dk\frac{\left(\alpha \sin (ka)\cos \left(ka\right)+k\right)-i\alpha {\sin }^2(ka)}{{\left(k\cos \left(ka\right)+\alpha \sin (ka)\right)}^2+k^2{\sin }^2(ka)}\\ A^2=D^2{k}^2\frac{{\left(\alpha \sin (ka)\cos \left(ka\right)+k\right)}^2+{\alpha }^2{\sin }^4(ka)}{{\left(k^2+2k\alpha \sin (ka)\cos \left(ka\right)+{\alpha }^2{\sin }^2(ka)\right)}^2}=D^2\frac{k^2}{k^2+2k\alpha \sin (ka)\cos \left(ka\right)+{\alpha }^2{\sin }^2(ka)}\\ A^2=D^2\frac{k^2}{k^2+k\alpha \sin (2ka)+\frac{{\alpha }^2}{2}\left(1-\cos (2ka)\right)}\end{array}}$

Derivamos respecto de k, para calcular los extremos (máximos y mínimos) de |A|²

${\displaystyle \begin{array}{l}\frac{d{A}^2}{dk}=0\\ k\left(1-\alpha a\right)\sin (2ka)-\left(\alpha +2k^{2}a\right)\cos (2ka)+\alpha =0\end{array}}$

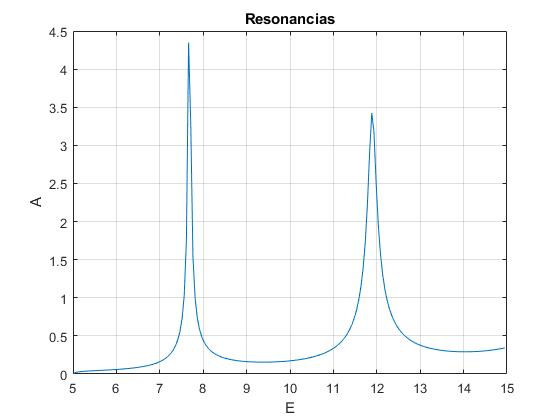
Establecemos un sistema de unidades en el que ℏ=m=1. Representamos la amplitud |A|² en función de la energía E, $k=\sqrt{2E}$. Resolvemos la ecuacion transcendente en k, calculando las energías E de los máximos y minimos de la amplitud

La posición de la barrera es a=3, el parámetro α=10

function resonancias
    ee=linspace(0,5,100); %energías
    a=3; %posición barrera
    alfa=20; %parámetro
    hold on
    g=@(k) (1-alfa*a)*k.*sin(2*k*a)-(alfa+2*k.^2*a).*cos(2*k*a)+alfa;
    k=sqrt(2*ee);
    rr=raices(g,k);
    disp(rr.^2/2)
    plot(rr.^2/2,0,'ro','markersize',3,'markerfacecolor','r')
    f=@(k) k./sqrt(k.^2+alfa*k.*sin(2*k*a)+alfa^2*(1-cos(2*k*a))/2);
    plot(ee,f(k))
    hold off
    xlabel('E')
    ylabel('A')
    grid on
    title('Resonancias')
    
    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for m=1:length(indices)
            r(m)=fzero(f, [x(indices(m)), x(indices(m)+1)]);
        end
    end 
end

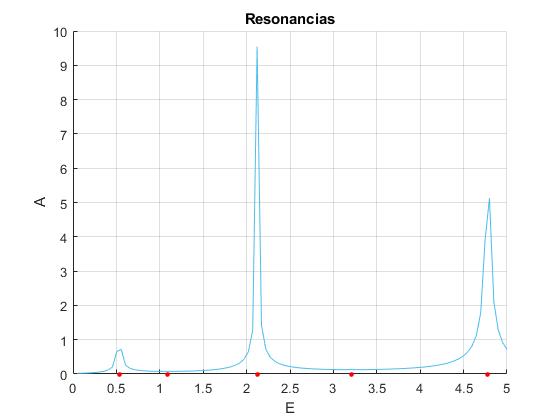
Los extremos se señalan mediante puntos de color rojo en la figura. Los mínimos corresponden al índice par y los máximos al impar

    0.5305    1.0866    2.1229    3.2131    4.7790

Caso particular

Cuando el parámetro α es muy grande, tenemos un pozo de potencial de anchura a y altura infinita.

${\displaystyle \begin{array}{l}k\left(\frac{1}{\alpha }-a\right)\sin (2ka)-\left(1+\frac{2k^{2}a}{\alpha }\right)\cos (2ka)+1=0\\ -ka\sin (2ka)-\cos (2ka)+1\approx 0\\ -2ka\sin (ka)\cos (ka)+2{\sin }^2(ka)=\mathrm{0,}\{\begin{array}{l}\sin (ka)=\mathrm{0,}ka=n\pi \\ \tan (ka)=ka\end{array}\end{array}}$

Los primeros corresponden a los niveles de energía de un pozo de potencial de altura infinita y de anchura a. Se advierte que en el apartado 'Pozo de potencial de profundidad infinita', la anchura del pozo de potencial es 2a

${\displaystyle \frac{n\pi }{a}=\sqrt{\frac{2m}{{\hslash }^2}E},E_n=\frac{n^2{\pi }^2{\hslash }^2}{2m{a}^2},n=\mathrm{1,2,3...}}$

function resonancia_1
    ee=linspace(0,5,100);
    a=3; %posición barrrera
    alfa=50; %parámetro
    %exacto
    g=@(k) (1-alfa*a)*k.*sin(2*k*a)-(alfa+2*k.^2*a).*cos(2*k*a)+alfa; %exacto
    k=sqrt(2*ee);
    rr=raices(g,k);
    disp(rr.^2/2)
    %aproximado (alfa grande)
    g=@(k) sin(k*a)-a*k.*cos(k*a); 
    rr=raices(g,k);
    aprox=sort([(1:length(rr))*pi/a,rr]);
    disp(aprox.^2/2)

    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for m=1:length(indices)
            r(m)=fzero(f, [x(indices(m)), x(indices(m)+1)]);
        end
    end 
end

Los mínimos corresponden al índice par y los máximos al impar

    0.5411    1.1071    2.1644    3.2725    4.8700 %exacto
    0.5483    1.1217    2.1932    3.3155           %aproximado

Funciones de onda

${\displaystyle \begin{array}{l}\{\begin{array}{l}{\psi }_I(x)=2iA\sin (kx),0<x<a\\ A=-Dk\frac{\left(\alpha \sin (ka)\cos \left(ka\right)+k\right)-i\alpha {\sin }^2(ka)}{{\left(k\cos \left(ka\right)+\alpha \sin (ka)\right)}^2+k^2{\sin }^2(ka)}\end{array}\\ \{\begin{array}{l}{\psi }_{II}(x)=C\exp (ikx)+D\exp (-ikx),x>a\\ C\exp (ika)=2iA\sin (ka)-D\exp (-ika)\end{array}\end{array}}$

Sea a=3, α=20, tomamos D=1. Representamos la función de onda, por ejemplo, para el segundo máximo de amplitud |A|², E=2.1229

a=3; %posición barrera
alfa=20; %parámetro
hold on
e=2.1229; %energía (máximo)
k=sqrt(2*e);
D=1;
A=-D*k*(alfa*sin(k*a)*cos(k*a)+k-1i*alfa*sin(k*a)^2)/
((k*cos(k*a)+alfa*sin(k*a))^2+k^2*sin(k*a)^2);
 C=(2*1i*A*sin(k*a)-D*exp(-1i*k*a))*exp(-1i*k*a);
disp(C*C') %comprobación |C|^2=1
fplot(@(x) real(2*1i*A*sin(k*x)),[0,a])
fplot(@(x) real(C*exp(1i*k*x)+D*exp(-1i*k*x)),[a,3*a]) 
hold off
xlabel('x')
ylabel('\Psi(x)')
grid on
title('Función de onda')

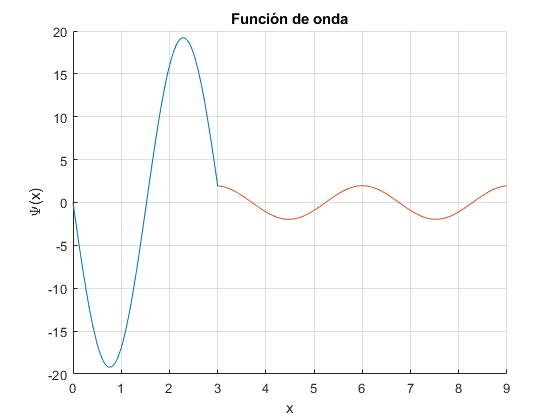
Cambiamos la energía al segundo mínimo, E=3.2131

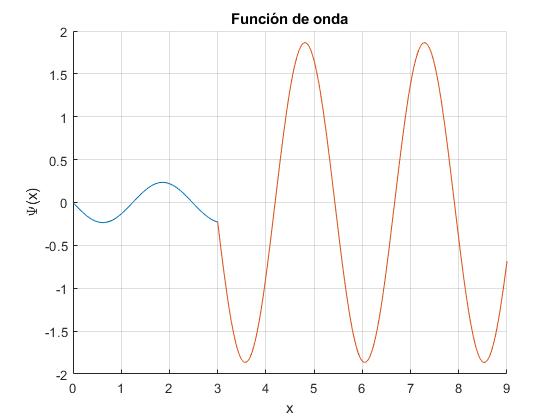
Comprobamos que el cuadrado de la amplitud de la función de onda de las partículas incidentes |D|² es igual a la de las reflejadas |C|²=1

   1.0000

Desfase

La representación gráfica de la función de onda en los intervalos 0<x<a y x>a, nos sugiere que la función de onda se puede simplificar cambiando de escala

${\displaystyle \{\begin{array}{l}{\psi }_I(x)=A\sin (kx),0<x<a\\ {\psi }_{II}(x)=\sin \left(k(x-a)+\delta \right),x>a\end{array}}$

La amplitud A y la fase δ se calculan a partir de las condiciones de continuidad

${\displaystyle \begin{array}{l}\{\begin{array}{l}{\psi }_I(a)={\psi }_{II}(a)\\ -\frac{{\hslash }^2}{2m}\left({\frac{d{\psi }_{II}(x)}{dx}|}_a-{\frac{d{\psi }_I(x)}{dx}|}_a\right)+\alpha \frac{{\hslash }^2}{2m}{\psi }_I(a)=0\end{array}\\ \{\begin{array}{l}A\sin (ka)=\sin \delta \\ -\left(k\cos \delta -kA\cos (ka)\right)+\alpha A\sin (ka)=0\end{array}\end{array}}$

Dividiendo las dos ecuaciones, eliminamos la amplitud A y despejamos la fase δ

${\displaystyle \tan \delta =\frac{\sin (ka)}{\cos (ka)+\frac{\alpha }{k}\sin (ka)}=\frac{\tan (ka)}{1+\frac{\alpha }{k}\tan (ka)}}$

La fase se anula, cuando sin(ka)=0, la energía es

${\displaystyle ka=n\pi ,E=\frac{n^2{\pi }^2}{2a^2},n=\mathrm{1,2,3...}}$

Tomamos la primera ecuación, utilizando la relación entre sinδ y tanδ, despejamos la amplitud A

${\displaystyle \begin{array}{l}\sin \delta =\frac{\tan \delta }{\sqrt{1+{\tan }^2\delta }}\\ A\sin (ka)=\frac{\sin (ka)}{\sqrt{{\sin }^2(ka)+{\left(\cos (ka)+\frac{\alpha }{k}\sin (ka\right)}^2}}\\ A=\frac{k}{\sqrt{k^2+2k\alpha \sin (ka)\cos \left(ka\right)+{\alpha }^2{\sin }^2(ka)}}\end{array}}$

El mismo resultado que hemos obtenido anteriormente

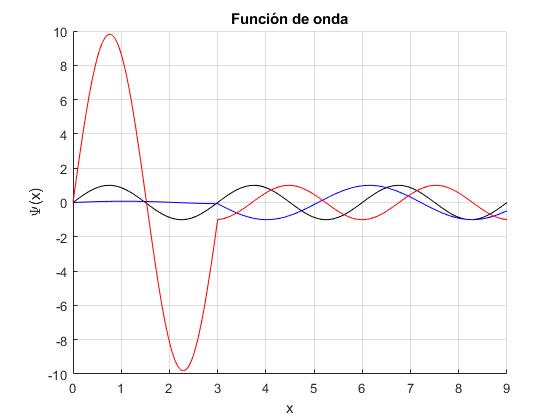
Con los datos, a=3, y α=20. Representamos la función de onda, para tres valores de la energía:

• Cuando están en fase, δ=0, para n=1, E=π²/(2a²)=2.1932, en color negro
• Primer mínimo, E=1.0866, en color azul
• Segundo máximo, E=2.1229, en color rojo

a=3; %posición barrera
alfa=20; %parámetro
hold on
colores=['k','b','r'];
j=1;
for e=[2.1932,1.0866,2.1229]
    k=sqrt(2*e);
    A=k/sqrt(k^2+2*alfa*k*sin(k*a)*cos(k*a)+(alfa*sin(k*a))^2);
    delta=atan2(sin(k*a), cos(k*a)+alfa*sin(k*a)/k);
    fplot(@(x) A*sin(k*x),[0,a], 'color',colores(j))
    fplot(@(x) sin(k*(x-a)+delta),[a,3*a],'color',colores(j))
    j=j+1;
end
hold off
xlabel('x')
ylabel('\Psi(x)')
grid on
title('Función de onda')

Pozo de potencial asimétrico con barrera

En la página titulada Otros potenciales rectangulares de potencial, estudiamos el potencial asimétrico de profundidad V₀ y anchura a, calculamos los niveles de energía y representamos las funciones de onda

En este apartado, le añadimos una barrera de potencial de altura V₁ y de anchura b, tal como se muestra en la figura

El interés de este ejemplo, estriba en el estudio de la amplitud de la función de onda en la cavidad (región I) cuando las partículas de masa m y energía V₀<E<V₀+V₁ inciden sobre la barrera

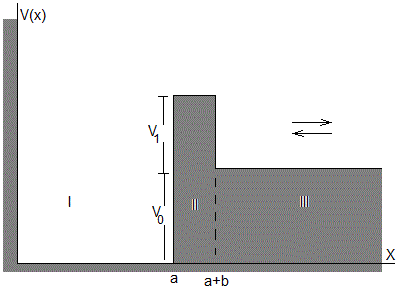
Estudiaremos las soluciones de la ecuación de Schrödinger para el potencial V(x) en los intervalos de energías E<V₀ y V₀<E<V₀+V₁

${\displaystyle \begin{array}{l}-\frac{{\hslash }^2}{2m}\frac{d^2\psi (x)}{d{x}^2}+V(x)·\psi (x)=E·\psi (x)\\ V(x)=\{\begin{array}{l}\infty ,x\le 0\\ \mathrm{0,}0<x\le a\\ V_0+V_1,a<x\le a+b\\ V_0,x>a+b\end{array}\end{array}}$

E<V₀

• Región I

${\displaystyle \begin{array}{l}\frac{d^2\psi }{d{x}^2}+\frac{2m}{{\hslash }^2}E·\psi =\mathrm{0,}{k}_1^2=\frac{2m}{{\hslash }^2}E\\ {\psi }_I(x)=A\exp (i{k}_{1}x)+B\exp (-i{k}_{1}x),0<x\le a\end{array}}$

Como el potencial es infinito en x=0, Ψ(0)=0, lo que implica que A+B=0. Las función de onda en este intervalo es

${\displaystyle {\psi }_I(x)=2iA\sin (k_{1}x),0<x\le a}$

• Región II

${\displaystyle \begin{array}{l}\frac{d^2\psi }{d{x}^2}-\frac{2m}{{\hslash }^2}\left(V_0+V_1-E\right)·\psi =\mathrm{0,}{\alpha }_2^2=\frac{2m}{{\hslash }^2}\left(V_0+V_1-E\right)\\ {\psi }_{II}(x)=C\exp (-{\alpha }_{2}x)+D\exp ({\alpha }_{2}x),a<x\le a+b\end{array}}$

• Región III

${\displaystyle \begin{array}{l}\frac{d^2\psi }{d{x}^2}-\frac{2m}{{\hslash }^2}\left(V_0-E\right)\psi =\mathrm{0,}{\alpha }_3^2=\frac{2m}{{\hslash }^2}\left(V_0-E\right)\\ {\psi }_{III}(x)=F\exp (-{\alpha }_{3}x)+G\exp ({\alpha }_{3}x),x>a+b\end{array}}$

El coeficiente G deberá de ser nulo para mantener la función de onda finita cuando x→∞

${\displaystyle {\psi }_{III}(x)=F\exp (-{\alpha }_{3}x),x>a+b}$

Las condiciones de continuidad de la función de onda y de su derivada primera son

• En x=a

${\displaystyle \begin{array}{l}\{\begin{array}{l}{\psi }_I(a)={\psi }_{II}(a)\\ {\frac{d{\psi }_I(x)}{dx}|}_{x=a}={\frac{d{\psi }_{II}(x)}{dx}|}_{x=a}\end{array}\\ \{\begin{array}{l}2iA\sin (k_{1}a)=C\exp (-{\alpha }_{2}a)+D\exp ({\alpha }_{2}a)\\ 2i{k}_{1}A\cos (k_{1}a)=-{\alpha }_{2}C\exp (-{\alpha }_{2}a)+{\alpha }_{2}D\exp ({\alpha }_{2}a)\end{array}\end{array}}$

Despejamos los coeficientes C y D en este sistema de dos ecuaciones

${\displaystyle \begin{array}{l}C=iA\frac{{\alpha }_2\sin (k_{1}a)-k_1\cos (k_{1}a)}{{\alpha }_2}\exp ({\alpha }_{2}a)\\ D=iA\frac{{\alpha }_2\sin (k_{1}a)+k_1\cos (k_{1}a)}{{\alpha }_2}\exp (-{\alpha }_{2}a)\end{array}}$

• En x=a+b

${\displaystyle \begin{array}{l}\{\begin{array}{l}{\psi }_{II}(a)={\psi }_{III}(a)\\ {\frac{d{\psi }_{II}(x)}{dx}|}_{x=a+b}={\frac{d{\psi }_{III}(x)}{dx}|}_{x=a+b}\end{array}\\ \{\begin{array}{l}C\exp \left(-{\alpha }_2(a+b)\right)+D\exp \left({\alpha }_2(a+b)\right)=F\exp \left(-{\alpha }_3(a+b)\right)\\ -{\alpha }_{2}C\exp \left(-{\alpha }_2(a+b)\right)+{\alpha }_{2}D\exp \left({\alpha }_2(a+b)\right)=-{\alpha }_{3}F\exp \left(-{\alpha }_3(a+b)\right)\end{array}\end{array}}$

Niveles de energía

Eliminamos F en este sistema de dos ecuaciones

${\displaystyle \left({\alpha }_3-{\alpha }_2\right)C\exp \left(-{\alpha }_2(a+b)\right)+\left({\alpha }_3+{\alpha }_2\right)D\exp \left({\alpha }_2(a+b)\right)=0}$

Junto con las expresiones de C y D obtenemos la ecuación transcendente de la energía E

${\displaystyle \left(\frac{{\alpha }_3}{{\alpha }_2}-1\right)\left({\alpha }_2\sin (k_{1}a)-k_1\cos (k_{1}a)\right)\exp \left(-{\alpha }_{2}b\right)+\left(\frac{{\alpha }_3}{{\alpha }_2}+1\right)\left({\alpha }_2\sin (k_{1}a)+k_1\cos (k_{1}a)\right)\exp \left({\alpha }_{2}b\right)=0}$

Calculamos y representamos los niveles de energía para un pozo de potencial de anchura a=3, profundidad V₀=5 y una barrera de anchura b=1 y altura V₁=2

function resonancia_3
    V0=5; %profundidad pozo
    a=3; %anchura pozo
    V1=2; %altura barrera
    b=1; %anchura barrera
    
    ee=linspace(0,V0, 20);
    rr=raices(@ecuacion,ee);
    disp(rr)
    %potencial
    xx=[-0.1, 0, 0, a, a, a+b, a+b,2*a, 2*a, -0.1, -0.1];
    yy=[V0+V1+1, V0+V1+1, 0, 0, V0+V1, V0+V1 V0, V0, -0.1, -0.1, V0+1];
    fill(xx,yy, [0.5 0.5 0.5])
    %niveles de energía
    for E=rr
        line([0,a+1],[E,E],'color','b')
        text(a, E,num2str(E),'VerticalAlignment','bottom', 
'HorizontalAlignment','right')
   end
    xlabel('')
    ylabel('E')
    title('Niveles de energía')
    
    function res=ecuacion(E)
        alfa_2=sqrt(2*(V1+V0-E));
        alfa_3=sqrt(2*(V0-E));
        k1=sqrt(2*E);
        res=(alfa_3./alfa_2-1).*(alfa_2.*sin(k1*a)-k1.*cos(k1*a)).*
exp(-alfa_2*b)+(alfa_3./alfa_2+1).*(alfa_2.*sin(k1*a)+k1.*cos(k1*a)).
*exp(alfa_2*b);
    end
    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

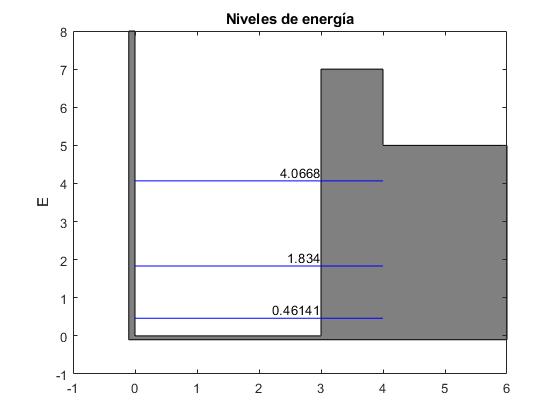
Los niveles de energía que hemos obtenido son muy parecidos a los de un potencial asimétrico para los mismo valores de la anchura a=3 y profundidad V₀=5

Funciones de onda

${\displaystyle \begin{array}{l}\{\begin{array}{l}{\psi }_I(x)=2iA\sin (k_{1}x),0<x\le a\\ {\psi }_{II}(x)=C\exp (-{\alpha }_{2}x)+D\exp ({\alpha }_{2}x),a<x\le a+b\\ {\psi }_{III}(x)=F\exp (-{\alpha }_{3}x),x>a+b\end{array}\\ C=iA\frac{{\alpha }_2\sin (k_{1}a)-k_1\cos (k_{1}a)}{{\alpha }_2}\exp ({\alpha }_{2}a)\\ D=iA\frac{{\alpha }_2\sin (k_{1}a)+k_1\cos (k_{1}a)}{{\alpha }_2}\exp (-{\alpha }_{2}a)\\ F=\left(C\exp \left(-{\alpha }_2(a+b)\right)+D\exp \left({\alpha }_2(a+b)\right)\right)\exp \left({\alpha }_3(a+b)\right)\end{array}}$

El coeficiente A o iA se calcula de modo que la integral

${\displaystyle {\displaystyle \underset{0}{\overset{a}{\int }}{\left|{\psi }_I(x)\right|}^{2}dx}+{\displaystyle \underset{a}{\overset{a+b}{\int }}{\left|{\psi }_{II}(x)\right|}^{2}dx}+{\displaystyle \underset{a+b}{\overset{\infty }{\int }}{\left|{\psi }_{III}(x)\right|}^{2}dx}=1}$

El resultado es

${\displaystyle \begin{array}{l}2A^2\left(a-\frac{\sin (2k_{1}a)}{2k_1}\right)+2CD·b-\frac{C^2}{2{\alpha }_2}\left(\exp \left(-2{\alpha }_2(a+b)\right)-\exp \left(-2{\alpha }_{2}a\right)\right)+\\ \frac{D^2}{2{\alpha }_2}\left(\exp \left(2{\alpha }_2(a+b)\right)-\exp \left(2{\alpha }_{2}a\right)\right)+\frac{F^2}{2{\alpha }_2}\exp \left(-2{\alpha }_3(a+b)\right)=1\end{array}}$

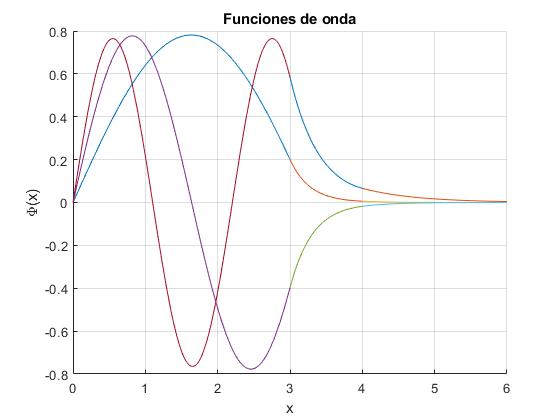
Representamos las funciones de onda, correspondientes a los tres niveles de energía. Vemos que son similares a las representadas para un pozo de potencial asimétrico, salvo que tienden a cero más rápidamente, al estar por encima, en la región II, una barrera de potencial de altura V₁.

function resonancia_4
    V0=5; %profundidad pozo
    a=3; %anchura pozo
    V1=2; %altura barrera
    b=1; %anchura barrera 
    ee=linspace(0,V0, 20);
    rr=raices(@ecuacion,ee);
    disp(rr)
    %funciones de onda
    hold on
    for E=rr
        alfa_2=sqrt(2*(V1+V0-E));
        alfa_3=sqrt(2*(V0-E));
        k1=sqrt(2*E);
        C=(alfa_2*sin(k1*a)-k1*cos(k1*a))*exp(alfa_2*a)/alfa_2;
        D=(alfa_2*sin(k1*a)+k1*cos(k1*a))*exp(-alfa_2*a)/alfa_2;
        F=(C*exp(-alfa_2*(a+b))+D*exp(alfa_2*(a+b)))*exp(alfa_3*(a+b));
       suma=2*(a-sin(2*k1*a)/(2*k1))+2*C*D*b-C^2*(exp(-2*alfa_2*(a+b))-
exp(-2*alfa_2*a))/(2*alfa_2)+D^2*(exp(2*alfa_2*(a+b))-exp(2*alfa_2*a))
/(2*alfa_2)+F^2*exp(-2*alfa_3*(a+b))/(2*alfa_3);
       A=1/sqrt(suma);
       f1=@(x) 2*A*sin(k1*x);
       f2=@(x) (C*exp(-alfa_2*x)+D*exp(alfa_2*x))*A;
       f3=@(x) A*F*exp(-alfa_3*x);
       fplot(f1,[0,a])
       fplot(f2,[a,a+b])
       fplot(f3,[a+b,2*a])
    end
    hold off
    grid on
    xlabel('x')
    ylabel('\Phi(x)')
    title('Funciones de onda')

     function res=ecuacion(E)
        alfa_2=sqrt(2*(V1+V0-E));
        alfa_3=sqrt(2*(V0-E));
        k1=sqrt(2*E);
        res=(alfa_3./alfa_2-1).*(alfa_2.*sin(k1*a)-k1.*cos(k1*a)).*
exp(-alfa_2*b)+(alfa_3./alfa_2+1).*(alfa_2.*sin(k1*a)+k1.*cos(k1*a)).
*exp(alfa_2*b);
    end
    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

V₀<E<V₁

• Región I

${\displaystyle \begin{array}{l}\frac{d^2\psi }{d{x}^2}+\frac{2m}{{\hslash }^2}E·\psi =\mathrm{0,}{k}_1^2=\frac{2m}{{\hslash }^2}E\\ {\psi }_I(x)=2iA\sin (k_{1}x),0<x\le a\end{array}}$

• Región II

${\displaystyle \begin{array}{l}\frac{d^2\psi }{d{x}^2}-\frac{2m}{{\hslash }^2}\left(V_0+V_1-E\right)\psi =\mathrm{0,}{\alpha }_2^2=\frac{2m}{{\hslash }^2}\left(V_0+V_1-E\right)\\ {\psi }_{II}(x)=C\exp (-{\alpha }_{2}x)+D\exp ({\alpha }_{2}x),a<x\le a+b\end{array}}$

• Región III

${\displaystyle \begin{array}{l}\frac{d^2\psi }{d{x}^2}+\frac{2m}{{\hslash }^2}\left(E-V_0\right)\psi =\mathrm{0,}{k}_3^2=\frac{2m}{{\hslash }^2}\left(E-V_0\right)\\ {\psi }_{III}(x)=F\exp (-i{k}_{3}x)+G\exp (i{k}_{3}x),x>a+b\end{array}}$

F es la amplitud del las partículas incidentes sobre la barrera (se mueven de derecha a izquierda) y G es la amplitud de las reflejadas (de izquierda a derecha), se deberá cumplir que los módulos |F|=|G|

Las condiciones de continuidad de la función de onda y de su derivada primera son

• En x=a

${\displaystyle \begin{array}{l}\{\begin{array}{l}{\psi }_I(a)={\psi }_{II}(a)\\ {\frac{d{\psi }_I(x)}{dx}|}_{x=a}={\frac{d{\psi }_{II}(x)}{dx}|}_{x=a}\end{array}\\ \{\begin{array}{l}2iA\sin (k_{1}a)=C\exp (-{\alpha }_{2}a)+D\exp ({\alpha }_{2}a)\\ 2i{k}_{1}A\cos (k_{1}a)=-{\alpha }_{2}C\exp (-{\alpha }_{2}a)+{\alpha }_{2}D\exp ({\alpha }_{2}a)\end{array}\end{array}}$

Despejamos los coeficientes C y D en el sistema de dos ecuaciones

${\displaystyle \begin{array}{l}C=iA\frac{{\alpha }_2\sin (k_{1}a)-k_1\cos (k_{1}a)}{{\alpha }_2}\exp ({\alpha }_{2}a)\\ D=iA\frac{{\alpha }_2\sin (k_{1}a)+k_1\cos (k_{1}a)}{{\alpha }_2}\exp (-{\alpha }_{2}a)\end{array}}$

• En x=a+b

${\displaystyle \begin{array}{l}\{\begin{array}{l}{\psi }_{II}(a)={\psi }_{III}(a)\\ {\frac{d{\psi }_{II}(x)}{dx}|}_{x=a+b}={\frac{d{\psi }_{III}(x)}{dx}|}_{x=a+b}\end{array}\\ \{\begin{array}{l}C\exp \left(-{\alpha }_2(a+b)\right)+D\exp \left({\alpha }_2(a+b)\right)=F\exp \left(-i{k}_3(a+b)\right)+G\exp \left(i{k}_3(a+b)\right)\\ -{\alpha }_{2}C\exp \left(-{\alpha }_2(a+b)\right)+{\alpha }_{2}D\exp \left({\alpha }_2(a+b)\right)=-i{k}_{3}F\exp \left(-i{k}_3(a+b)\right)+i{k}_{3}G\exp \left(i{k}_3(a+b)\right)\end{array}\end{array}}$

Despejamos F y G en este sistema de dos ecuaciones

${\displaystyle \{\begin{array}{l}\left(i{k}_3+{\alpha }_2\right)C\exp \left(-{\alpha }_2(a+b)\right)+\left(i{k}_3-{\alpha }_2\right)D\exp \left({\alpha }_2(a+b)\right)=2i{k}_{3}F\exp \left(-i{k}_3(a+b)\right)\\ \left(i{k}_3-{\alpha }_2\right)C\exp \left(-{\alpha }_2(a+b)\right)+\left(i{k}_3+{\alpha }_2\right)D\exp \left({\alpha }_2(a+b)\right)=2i{k}_{3}G\exp \left(i{k}_3(a+b)\right)\end{array}}$

Sustituyendo C y D en la primera ecuación, relacionamos A y F

${\displaystyle F=\frac{A}{{\alpha }_2{k}_3}\exp \left(i{k}_3(a+b)\right)\left\{\begin{array}{l}-{\alpha }_2\left({\alpha }_2\sin (k_{1}a)\sinh ({\alpha }_{2}b)+k_1\cos (k_{1}a)\cosh ({\alpha }_{2}b)\right)\\ +i{k}_3\left({\alpha }_2\sin (k_{1}a)\cosh ({\alpha }_{2}b)+k_1\cos (k_{1}a)\sinh ({\alpha }_{2}b)\right)\end{array}\right\}}$

Sustituyendo C y D en la segunda ecuación, relacionamos A y G

${\displaystyle G=\frac{A}{{\alpha }_2{k}_3}\exp \left(-i{k}_3(a+b)\right)\left\{\begin{array}{l}{\alpha }_2\left({\alpha }_2\sin (k_{1}a)\sinh ({\alpha }_{2}b)+k_1\cos (k_{1}a)\cosh ({\alpha }_{2}b)\right)+\\ i{k}_3\left({\alpha }_2\sin (k_{1}a)\cosh ({\alpha }_{2}b)+k_1\cos (k_{1}a)\sinh ({\alpha }_{2}b)\right)\end{array}\right\}}$

Comprobamos que los módulos de F y G son iguales

Despejamos el módulo de la amplitud |A| tomando el de |F| como unidad

${\displaystyle \left|A\right|=\frac{{\alpha }_2{k}_3}{\sqrt{{\alpha }_2^2{\left({\alpha }_2\sin (k_{1}a)\sinh ({\alpha }_{2}b)+k_1\cos (k_{1}a)\cosh ({\alpha }_{2}b)\right)}^2+k_3^2{\left({\alpha }_2\sin (k_{1}a)\cosh ({\alpha }_{2}b)+k_1\cos (k_{1}a)\sinh ({\alpha }_{2}b)\right)}^2}}\left|F\right|}$

Representamos el módulo de |A| en función de la energía V₀<E<V₀+V₁, para la anchura del pozo a=3, profundidad V₀=5, anchura de la barrera b=0.5, altura V₁=10. Observamos que para ciertos valores de la energía E el módulo de |A| presenta máximos, similares al ejemplo estudiado en el apartado anterior

V0=5; %profundidad pozo
a=3; %anchura pozo
V1=10; %altura barrera
b=0.5; %anchura barrera
ee=linspace(V0,V0+V1, 200);
j=1;
A=zeros(1, length(ee));
for E=ee
    alfa_2=sqrt(2*(V1+V0-E));
    k3=sqrt(2*(E-V0));
    k1=sqrt(2*E);
    A(j)=alfa_2*k3/sqrt(alfa_2^2*(alfa_2*sin(k1*a)*sinh(alfa_2*b)
+k1*cos(k1*a)*cosh(alfa_2*b))^2+k3^2*(alfa_2*sin(k1*a)*cosh(alfa_2*b)
+k1*cos(k1*a)*sinh(alfa_2*b))^2);
    j=j+1;
end
plot(ee,A)
grid on
xlabel('E')
ylabel('A')
title('Resonancias')

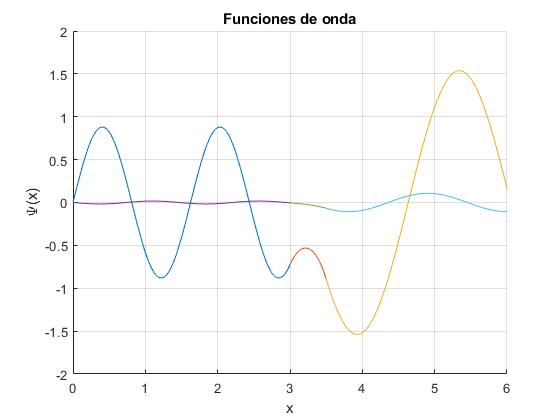
Representamos la función de onda para un valor de la energía E cercano a un máximo y para un valor cercano a un mínimo.

V0=5; %profundidad pozo
a=3; %anchura pozo
V1=10; %altura barrera
b=0.5; %anchura barrera
%funciones de onda
hold on
for E=[7.47,9.12]
    alfa_2=sqrt(2*(V1+V0-E));
    k3=sqrt(2*(E-V0));
    k1=sqrt(2*E);
    F=1;
    A=alfa_2*k3*exp(-1i*k3*(a+b))/(-alfa_2*(alfa_2*sin(k1*a)*
sinh(alfa_2*b)+k1*cos(k1*a)*cosh(alfa_2*b))+1i*k3*(alfa_2*sin(k1*a)*
cosh(alfa_2*b)+k1*cos(k1*a)*sinh(alfa_2*b)));
    C=(alfa_2*sin(k1*a)-k1*cos(k1*a))*exp(alfa_2*a)*1i*A/alfa_2;
    D=(alfa_2*sin(k1*a)+k1*cos(k1*a))*exp(-alfa_2*a)*1i*A/alfa_2;
    G=(C*exp(-alfa_2*(a+b))+D*exp(alfa_2*(a+b))-F*exp(-1i*k3*(a+b)))*
exp(-1i*k3*(a+b));
    f1=@(x) real(2*A*1i*sin(k1*x));
    f2=@(x) real(C*exp(-alfa_2*x)+D*exp(alfa_2*x));
    f3=@(x) real(F*exp(-1i*k3*x)+G*exp(1i*k3*x));
    fplot(f1,[0,a])
    fplot(f2,[a,a+b])
    fplot(f3,[a+b,2*a])
end
hold off
grid on
xlabel('x')
ylabel('\Psi(x)')
title('Funciones de onda')

Referencias

Herbert Massmann. Illustration of resonances and the law of exponential decay in a simple quantum-mechanical problem. Am. J. Phys. 53 (7) July 1985, pp. 679-683

One Dimensional Scattering.