Barrera de potencial de forma cualesquiera

Consideremos un haz de partículas de masa m y energía E que inciden sobre una barrera de potencial V(x).

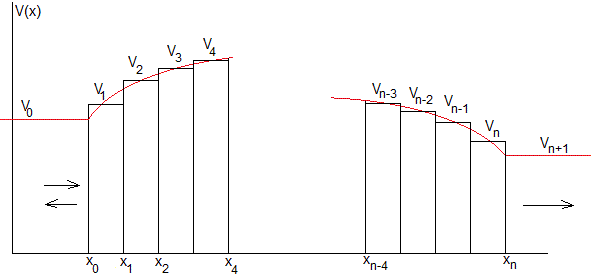
El potencial descrito por la función continua V(x) (color rojo) se aproxima por una función escalonada de altura V_j (j=1, 2, 3,..n), en color negro, valor medio

$\begin{array}{l} V_{j} = \frac{1}{2} (V (x_{j - 1}) + V (x_{j})), j = 1,2,3... n \\ x_{j} = x_{0} + j h \end{array}$

Otro posible criterio para definir V_j es que el área del rectángulo V_j·h, sea igual al área bajo la curva en el intervalo (x_j-1, x_j)

$V_{j} = \frac{1}{h} \int_{x_{j - 1}}^{x_{j}} V (x) d x$

Vamos a obtener la solución de la ecuación de Schrödinger

Para el potencial constante V_j, en el intervalo (x_j-1, x_j)

$\begin{array}{l} \frac{d^{2} ψ_{j}}{d x^{2}} + \frac{2 m}{ℏ^{2}} (E - V_{j}) ψ_{j} = 0, k_{j} = \sqrt{\frac{2 m}{ℏ^{2}} (E - V_{j})}, j = 1,2... n \\ ψ_{j} (x) = A_{j} \exp (i k_{j} x) + B_{j} \exp (- i k_{j} x), x_{j - 1} < x \leq x_{j} \end{array}$

En el extremo izquierdo, la solución es

$\begin{array}{l} \frac{d^{2} ψ_{0}}{d x^{2}} + \frac{2 m}{ℏ^{2}} (E - V_{0}) ψ_{0} = 0, k_{0} = \sqrt{\frac{2 m}{ℏ^{2}} (E - V_{0})} \\ ψ_{0} (x) = A_{0} \exp (i k_{0} x) + B_{0} \exp (- i k_{0} x), - \infty < x \leq x_{0} \end{array}$

En el extremo derecho, la solución es

$\begin{array}{l} \frac{d^{2} ψ_{n + 1}}{d x^{2}} + \frac{2 m}{ℏ^{2}} (E - V_{n + 1}) ψ_{n + 1} = 0, k_{n + 1} = \sqrt{\frac{2 m}{ℏ^{2}} (E - V_{n + 1})} \\ ψ_{n + 1} (x) = A_{n + 1} \exp (i k_{n + 1} x), x > x_{n} \end{array}$

No hay partículas que se muevan de derecha hacia la izquierda, por lo que B_n+1=0

V_j puede ser mayor o menor que la energía E.

Las condiciones de continuidad de la función de onda y de su derivada primera en los puntos x₀, x₁, x₂, ...x_n son

En x₀

$\begin{array}{l} {\begin{cases} A_{0} e^{i k_{0} x_{0}} + B_{0} e^{- i k_{0} x_{0}} = A_{1} e^{i k_{1} x_{0}} + B_{1} e^{- i k_{1} x_{0}} \\ i k_{0} A_{0} e^{i k_{0} x_{0}} - i k_{0} B_{0} e^{- i k_{0} x_{0}} = i k_{1} A_{1} e^{i k_{1} x_{0}} - i k_{1} B_{1} e^{- i k_{1} x_{0}} \end{cases} \\ (\begin{matrix} e^{i k_{0} x_{0}} & e^{- i k_{0} x_{0}} \\ i k_{0} e^{i k_{0} x_{0}} & - i k_{0} e^{- i k_{0} x_{0}} \end{matrix}) (\begin{matrix} A_{0} \\ B_{0} \end{matrix}) = (\begin{matrix} e^{i k_{1} x_{0}} & e^{- i k_{1} x_{0}} \\ i k_{1} e^{i k_{1} x_{0}} & - i k_{1} e^{i k_{1} x_{0}} \end{matrix}) (\begin{matrix} A_{1} \\ B_{1} \end{matrix}) \\ (\begin{matrix} A_{1} \\ B_{1} \end{matrix}) = {(K_{1}^{- 1} K_{0})}_{x_{0}} (\begin{matrix} A_{0} \\ B_{0} \end{matrix}) \end{array}$

En x₁

$\begin{array}{l} {\begin{cases} A_{1} e^{i k_{1} x_{1}} + B_{1} e^{- i k_{1} x_{1}} = A_{2} e^{i k_{2} x_{1}} + B_{2} e^{- i k_{2} x_{1}} \\ i k_{1} A_{1} e^{i k_{1} x_{1}} - i k_{1} B_{1} e^{- i k_{1} x_{1}} = i k_{2} A_{2} e^{i k_{2} x_{1}} - i k_{2} B_{2} e^{- i k_{2} x_{1}} \end{cases} \\ (\begin{matrix} e^{i k_{1} x_{1}} & e^{- i k_{1} x_{1}} \\ i k_{1} e^{i k_{1} x_{1}} & - i k_{1} e^{- i k_{1} x_{1}} \end{matrix}) (\begin{matrix} A_{1} \\ B_{1} \end{matrix}) = (\begin{matrix} e^{i k_{2} x_{1}} & e^{- i k_{2} x_{1}} \\ i k_{2} e^{i k_{2} x_{1}} & - i k_{2} e^{- i k_{2} x_{1}} \end{matrix}) (\begin{matrix} A_{2} \\ B_{2} \end{matrix}) \\ (\begin{matrix} A_{2} \\ B_{2} \end{matrix}) = {(K_{2}^{- 1} K_{1})}_{x_{1}} (\begin{matrix} A_{1} \\ B_{1} \end{matrix}) \end{array}$

En x_j

$\begin{array}{l} {\begin{cases} A_{j} e^{i k_{j} x_{j}} + B_{j} e^{- i k_{j} x_{j}} = A_{j + 1} e^{i k_{j + 1} x_{j}} + B_{j + 1} e^{- i k_{j + 1} x_{j}} \\ i k_{j} A_{j} e^{i k_{j} x_{j}} - i k_{j} B_{j} e^{- i k_{j} x_{j}} = i k_{j + 1} A_{j + 1} e^{i k_{j + 1} x_{j}} - i k_{j + 1} B_{j + 1} e^{- i k_{j + 1} x_{j}} \end{cases} \\ (\begin{matrix} e^{i k_{j} x_{j}} & e^{- i k_{j} x_{j}} \\ i k_{j} e^{i k_{j} x_{j}} & - i k_{j} e^{- i k_{j} x_{j}} \end{matrix}) (\begin{matrix} A_{j} \\ B_{j} \end{matrix}) = (\begin{matrix} e^{i k_{j + 1} x_{j}} & e^{- i k_{j + 1} x_{j}} \\ i k_{j + 1} e^{i k_{j + 1} (x_{0} + j h)} & - i k_{j + 1} e^{- i k_{j + 1} x_{j}} \end{matrix}) (\begin{matrix} A_{j + 1} \\ B_{j + 1} \end{matrix}) \\ (\begin{matrix} A_{j + 1} \\ B_{j + 1} \end{matrix}) = {(K_{j + 1}^{- 1} K_{j})}_{x_{j}} (\begin{matrix} A_{j} \\ B_{j} \end{matrix}) \\ (\begin{matrix} A_{j + 1} \\ B_{j + 1} \end{matrix}) = \frac{1}{2} (\begin{matrix} (1 + \frac{k_{j}}{k_{j + 1}}) \exp (- i (k_{j + 1} - k_{j}) x_{j}) & (1 - \frac{k_{j}}{k_{j + 1}}) \exp (- i (k_{j + 1} + k_{j}) x_{j}) \\ (1 - \frac{k_{j}}{k_{j + 1}}) \exp (i (k_{j + 1} + k_{j}) x_{j}) & (1 + \frac{k_{j}}{k_{j + 1}}) \exp (i (k_{j + 1} - k_{j}) x_{j}) \end{matrix}) (\begin{matrix} A_{j} \\ B_{j} \end{matrix}) \end{array}$

En x_n

$\begin{array}{l} {\begin{cases} A_{n} e^{i k_{n} x_{n}} + B_{n} e^{- i k_{n} x_{n}} = A_{n + 1} e^{i k_{n + 1} x_{n}} + B_{n + 1} e^{- i k_{n + 1} x_{n}} \\ i k_{n} A_{n} e^{i k_{n} x_{n}} - i k_{n} B_{n} e^{- i k_{n} x_{n}} = i k_{n + 1} A_{n + 1} e^{i k_{n + 1} x_{n}} - i k_{n + 1} B_{n + 1} e^{- i k_{n + 1} x_{n}} \end{cases} \\ (\begin{matrix} e^{i k_{n} x_{n}} & e^{- i k_{n} x_{n}} \\ i k_{n} e^{i k_{n} x_{n}} & - i k_{n} e^{- i k_{n} x_{n}} \end{matrix}) (\begin{matrix} A_{n} \\ B_{n} \end{matrix}) = (\begin{matrix} e^{i k_{n + 1} x_{n}} & e^{- i k_{n + 1} x_{n}} \\ i k_{n + 1} e^{i k_{n + 1} x_{n}} & - i k_{n + 1} e^{- i k_{n + 1} x_{n}} \end{matrix}) (\begin{matrix} A_{n + 1} \\ B_{n + 1} \end{matrix}) \\ (\begin{matrix} A_{n + 1} \\ B_{n + 1} \end{matrix}) = {(K_{n + 1}^{- 1} K_{n})}_{x_{n}} (\begin{matrix} A_{n} \\ B_{n} \end{matrix}) \end{array}$

El resultado final es

$\begin{array}{l} (\begin{matrix} A_{n + 1} \\ B_{n + 1} \end{matrix}) = {(K_{n + 1}^{- 1} K_{n})}_{x_{n}} .... {(K_{j + 1}^{- 1} K_{j})}_{x_{j}} ... {(K_{2}^{- 1} K_{1})}_{x_{1}} {(K_{1}^{- 1} K_{0})}_{x_{0}} (\begin{matrix} A_{0} \\ B_{0} \end{matrix}) \\ (\begin{matrix} A_{n + 1} \\ 0 \end{matrix}) = (\begin{matrix} t_{11} & t_{12} \\ t_{21} & t_{22} \end{matrix}) (\begin{matrix} A_{0} \\ B_{0} \end{matrix}), {\begin{cases} A_{n + 1} = t_{11} A + t_{12} B_{0} \\ 0 = t_{21} A + t_{22} B_{0} \end{cases} \\ B_{0} = - \frac{t_{21}}{t_{22}} A_{0}, A_{n + 1} = (t_{11} - \frac{t_{21} t_{12}}{t_{22}}) A_{0} \end{array}$

Se definen los coeficientes de reflexión R y transmisión T

$R = \frac{{| B_{0} |}^{2}}{{| A_{0} |}^{2}}, T = \frac{k_{n + 1}}{k_{0}} \frac{{| A_{n + 1} |}^{2}}{{| A_{0} |}^{2}}$

Nota: Matriz inversa de una matriz cuadrada

$\begin{array}{l} {(\begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix})}^{- 1} = \frac{1}{| \begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix} |} (\begin{matrix} a_{22} & - a_{12} \\ - a_{21} & a_{11} \end{matrix}) \\ {(\begin{matrix} e^{i k x} & e^{- i k x} \\ i k e^{i k x} & - i k e^{- i k x} \end{matrix})}^{- 1} = \frac{1}{2} (\begin{matrix} e^{- i k x} & \frac{e^{- i k x}}{i k} \\ e^{i k x} & - \frac{e^{i k x}}{i k} \end{matrix}) \end{array}$

Coeficiente de transmisión del potencial V(x)

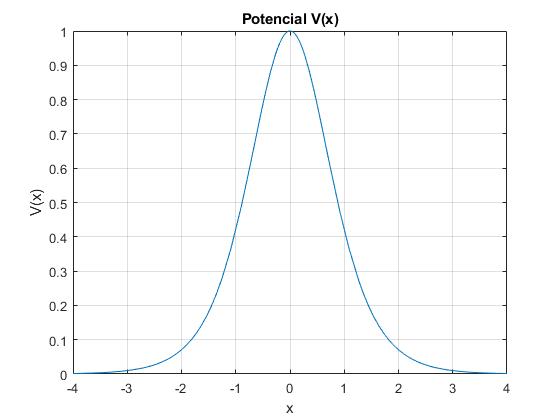
Sea una potencial en forma de campana

$V (x) = \frac{V_{0}}{\cosh^{2} (\frac{x}{a})}$

V0=1;
a=1;
V=@(x) V0./cosh(x/a).^2;
fplot(V, [-4*a,4*a])
xlabel('x')
ylabel('V(x)')
grid on
title('Potencial V(x)')

Solución exacta

La solución de la ecuación de Schrödinger para este potencial es complicada. La fórmula para el coeficiente de transmisión es (Landau, Lifshitz)

$\begin{array}{l} T = {\begin{cases} \frac{\sinh^{2} (π k a)}{\sinh^{2} (π k a) + \cos^{2} (\frac{1}{2} π \sqrt{1 - \frac{8 m V_{0} a^{2}}{ℏ^{2}}})}, \frac{8 m V_{0} a^{2}}{ℏ^{2}} < 1 \\ \frac{\sinh^{2} (π k a)}{\sinh^{2} (π k a) + \cosh^{2} (\frac{1}{2} π \sqrt{\frac{8 m V_{0} a^{2}}{ℏ^{2}} - 1})}, \frac{8 m V_{0} a^{2}}{ℏ^{2}} > 1 \end{cases} \\ k = \sqrt{\frac{2 m}{ℏ^{2}} E} \end{array}$

En este script comparamos la solución aproximada y la exacta para este potencial V(x) con V₀=10, a=0.25. La solución exacta es la segunda de las dos posibles fórmulas

V0=10;
a=0.25;
ee=linspace(0,V0,100);
T=zeros(1,length(ee));
R=zeros(1,length(ee));
%aproximada
x0=-4*a; %partida
n=50;
h=8*a/(n-1); %intervalo h
V=@(x) V0./cosh(x/a).^2; %función potencial
m=1;
for e=ee
    Vp=V(x0);
    k1=sqrt(2*(e-Vp));
    Vp=(V(x0)+V(x0+h))/2;
    k2=sqrt(2*(e-Vp));
    M=[(1+k1/k2)*exp(-1i*(k2-k1)*x0), (1-k1/k2)*exp(-1i*(k2+k1)*x0); 
(1-k1/k2)*exp(1i*(k2+k1)*x0),(1+k1/k2)*exp(1i*(k2-k1)*x0)]/2; 
    k1=k2;
    for j=1:n
        if j==n 
            break;
        end
        Vp=(V(x0+j*h)+V(x0+(j+1)*h))/2;
        k2=sqrt(2*(e-Vp));
        K=[(1+k1/k2)*exp(-1i*(k2-k1)*(x0+j*h)), (1-k1/k2)*exp(-1i*(k2+k1)*
(x0+j*h)); (1-k1/k2)*exp(1i*(k2+k1)*(x0+j*h)),(1+k1/k2)*exp(1i*(k2-k1)*
(x0+j*h))]/2; 
        M=K*M;
        k1=k2;
    end
    Vp=V(x0+n*h);
    k2=sqrt(2*(e-Vp));
    K=[(1+k1/k2)*exp(-1i*(k2-k1)*(x0+n*h)), (1-k1/k2)*exp(-1i*(k2+k1)*
(x0+n*h)); (1-k1/k2)*exp(1i*(k2+k1)*(x0+n*h)),(1+k1/k2)*exp(1i*(k2-k1)*
(x0+n*h))]/2; 
    M=K*M;
    B=-M(2,1)/M(2,2);
    C=M(1,1)+M(1,2)*B;
    T(m)=abs(C)^2;
    R(m)=abs(B)^2;
    m=m+1;
end
%exacta
k=sqrt(2*ee);
if 8*V0*a^2<1
    T1=sinh(pi*k*a).^2./(sinh(pi*k*a).^2+cos(pi*sqrt(1-8*V0*a^2)/2)^2);
else
    T1=sinh(pi*k*a).^2./(sinh(pi*k*a).^2+cosh(pi*sqrt(8*V0*a^2-1)/2)^2);
end
hold on
plot(ee,T); %aproximada
plot(ee,T1); %excata
hold off
grid on
legend('aproximada','exacta','location','best')
xlabel('E')
ylabel('T')
title('Coeficiente de transmisión')

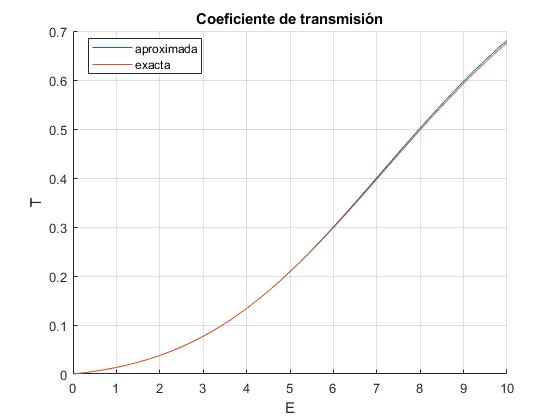
La solución exacta y aproximada apenas se diferencian

Cambiamos el valor del parámetro a=0.1, de modo que la solución exacta del coeficiente de transmisión sea la primera fórmula

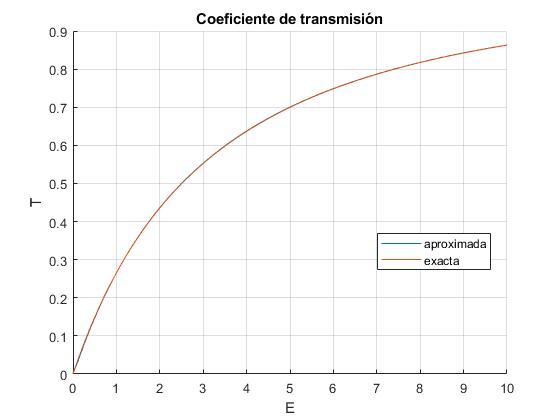
La solución exacta y aproximada coinciden.

Barrera en forma triangular

En la página titulada Escalón lineal y barrera de potencial de forma triangular calculamos el coeficiente de transmisión de una barrera de forma triangular como una aplicación de la funciones de Airy

Aproximamos la doble función lineal V(x) mediante una función escalonada

V0=10;
a=0.25;
ee=linspace(0,V0,100);
T=zeros(1,length(ee));
R=zeros(1,length(ee));
x0=-a;
n=20;
h=2*a/(n-1);
V=@(x) (x>-a & x<0).*(V0*x/a+V0)+(x>=0 & x<a).*(-V0*x/a+V0); %función potencial
m=1;
for e=ee
    Vp=V(x0);
    k1=sqrt(2*(e-Vp));
    Vp=(V(x0)+V(x0+h))/2;
    k2=sqrt(2*(e-Vp));
    M=[(1+k1/k2)*exp(-1i*(k2-k1)*x0), (1-k1/k2)*exp(-1i*(k2+k1)*x0); 
(1-k1/k2)*exp(1i*(k2+k1)*x0),(1+k1/k2)*exp(1i*(k2-k1)*x0)]/2; 
    k1=k2;
    for j=1:n
        if j==n 
            break;
        end
        Vp=(V(x0+j*h)+V(x0+(j+1)*h))/2;
        k2=sqrt(2*(e-Vp));
        K=[(1+k1/k2)*exp(-1i*(k2-k1)*(x0+j*h)), (1-k1/k2)*exp(-1i*(k2+k1)*
(x0+j*h)); (1-k1/k2)*exp(1i*(k2+k1)*(x0+j*h)),(1+k1/k2)*exp(1i*(k2-k1)*
(x0+j*h))]/2; 
        M=K*M;
        k1=k2;
    end
    Vp=V(x0+n*h);
    k2=sqrt(2*(e-Vp));
    K=[(1+k1/k2)*exp(-1i*(k2-k1)*(x0+n*h)), (1-k1/k2)*exp(-1i*(k2+k1)*
(x0+n*h)); (1-k1/k2)*exp(1i*(k2+k1)*(x0+n*h)),(1+k1/k2)*exp(1i*(k2-k1)
*(x0+n*h))]/2; 
    M=K*M;
    B=-M(2,1)/M(2,2);
    C=M(1,1)+M(1,2)*B;
    T(m)=abs(C)^2; %barrera 
    R(m)=abs(B)^2;
    m=m+1;
end
plot(ee,T); %aproximada
grid on
xlabel('E')
ylabel('T')
title('Coeficiente de transmisión')

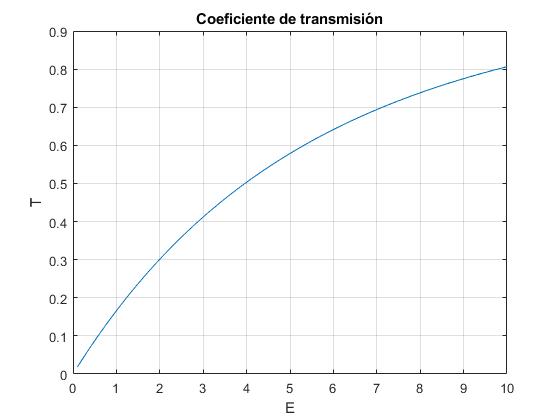
Obtenemos una gráfica similar a la que aparece al final de la página titulada Escalón lineal y barrera de potencial de forma triangular

Referencias

T. M. Kalotas, A. R. Lee. A new approach to one-dimensional scattering. Am. J. Phys. 59 (1) January 1991, pp. 48-51

Landau, Lifshitz. Física Teórica. Mecánica Cuántica (Teoría No-Relativista). Editorial Reverté (1972), pág. 94