Un modelo simple de núcleo radioactivo

Un núcleo está formado por protones y neutrones, la agrupación de dos protones y dos neutrones se denomina partícula alfa. La partícula alfa está confinada en el núcleo por las fuerzas de interacción fuerte, su energía E es menor que la altura de la barrera de potencial V₀.

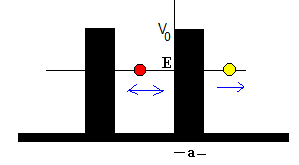
La partícula alfa se mueve en el interior del núcleo reflejándose en las paredes de la barrera con cierta frecuencia característica pero sin poderlo abandonar.

Las partículas alfa en cada choque con las paredes del núcleo, tienen cierta probabilidad de abandonarlo y ésta, depende fuertemente de la anchura de la barrera de potencial. Cuando una partícula alfa abandona el núcleo de un elemento radioactivo por efecto túnel, se transforma en otro cuya masa es cuatro unidades menor y está situado dos lugares antes en la Tabla Periódica.

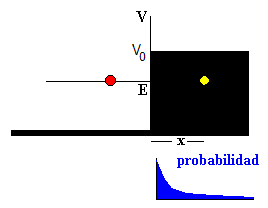
En la figura se muestra la probabilidad de encontrar una partícula de energía E<V₀, a una distancia x del origen en el interior de la región prohibida desde el punto de vista de la Mecánica Clásica. Como vimos en el estudio del escalón de potencial, la probabilidad por unidad de longitud viene dada por una función exponencial decreciente.

Por tanto, una partícula no puede penetrar demasiado a la derecha del origen. La probabilidad también disminuye con la masa de la partícula. Partículas como un protón o una partícula alfa tienen muy poca probabilidad de penetrar más allá del origen.

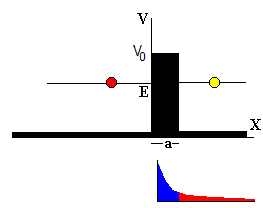
Una barrera de potencial consta de dos escalones. Una partícula incidente cuya energía E<V₀, no puede encontrarse en la región x>a ya que tendría que pasar a través de una región (la barrera de potencial) en la que su energía cinética es negativa. Desde el punto de vista cuántico tal paso es posible.

En una primera aproximación, podemos decir, que si la partícula penetra una distancia x>a en el escalón de potencial, al cortar el escalón y formar una barrera de anchura a, la partícula atravesará dicha dicha barrera encontrándose en la región x>a, y moviéndose hacia la derecha con una velocidad igual a la incidente (la energía potencial es cero). Decimos que dicha partícula ha atravesado la barrera de potencial por "efecto túnel".

Supongamos que sea T el coeficiente de transmisión de la partícula alfa a través de las paredes del núcleo radioactivo. Y sea P el periodo del movimiento de la partícula alfa en el interior del núcleo. La partícula alfa realiza 2/P intentos por unidad de tiempo de atravesar el núcleo por efecto túnel. La probabilidad en la unidad de tiempo de que se desintegre será λ=2T/P. La probabilidad de que el núcleo se desintegre en el tiempo dt es de λdt.

Si hay N núcleos presentes (siendo N muy grande) entonces en un tiempo dt se desintegrarán N(λdt) núcleos. El número de núcleos radiactivos disminuye a consecuencia de la desintegración

dN=-N(λdt)

integrando y teniendo en cuenta que en el instante t=0, el número inicial de núcleos radioactivos presentes es N₀.

${\displaystyle {\displaystyle \underset{N_0}{\overset{N}{\int }}\frac{dN}{N}}={\displaystyle \underset{0}{\overset{t}{\int }}-\lambda dt}N=N_0\exp (-\lambda t)}$

Actividades

Se introduce

• la anchura de la barrera entre los valores indicados en en el control titulado Anchura
• la energía de la partícula, en el control de edición titulado Energía, entre los valores indicados.

Se pulsa en el botón Nuevo, para que la partícula alfa comience a moverse hacia atrás y hacia adelante dentro del núcleo radioactivo, en cada intento tiene una probabilidad no nula de atravesar la barrera de potencial por efecto túnel.

Observar que no podemos predecir cuando un núcleo radioactivo se desintegra, tan sólo que la probabilidad de desintegración disminuye fuertemente al incrementar la anchura de la barrera de potencial.

Modelo de desintegración radioactiva alfa

Un núcleo tiene forma esférica pero no tiene un contorno bien definido, por lo que se ha de definir lo que se entiende por radio del núcleo.

La densidad del material de que está hecho el núcleo varía con la distancia al centro, siendo aproximadamente constante hasta cierta distancia y luego, decrece a cero en la superficie del núcleo. El radio R del núcleo se define como la distancia al centro desde el punto en que la densidad ha disminuido a la mitad de su valor en el centro. El radio del núcleo se determina experimentalmente a partir de experimentos de dispersión

Los resultados muestran que el R radio del núcleo

${\displaystyle R=r_0{A}^{\frac{1}{3}}}$

donde A es el número másico (número de protones Z más número de neutrones) y r₀=1.4·10^-15 m es constante para todos los núcleos

El volumen de un núcleo, una esfera de radio R

${\displaystyle V=\frac{4}{3}\pi {\left(r_0{A}^{\frac{1}{3}}\right)}^3=\frac{4}{3}\pi r_0^{3}A}$

La masa de un núcleo es m=1.66·10^-27·A, donde 1.66·10^-27 kg es la masa de un nucleón (protón o neutrón)

La densidad es constante e independiente de A, ρ=m/V=1.44·10¹⁷ kg/m³

Sea un núcleo radioactivo de número másico A y carga (número de protones) Z. Las partículas alfa (A=4, Z=2) oscilan en el interior del núcleo, deformándolo. La barrera de potencial les impide salir del núcleo. Cuando la partícula alfa penetra la barrera de potencial, el núcleo resultante (A-4, Z-2) y la partícula alfa se repelen produciéndose la desintegración del núcleo radioactivo.

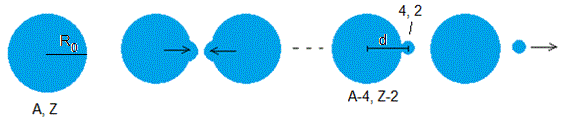
La constante de desintegración es $\lambda =\frac{v}{2R_0}T$ , donde v es la velocidad de la partícula alfa en el interior del núcleo radioactivo, R₀ es el radio del núcleo sin desintegrar y T es el coeficiente de transmisión que vamos a determinar mediante el siguiente modelo

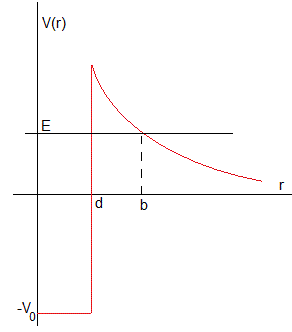
El potencial V(r) se debe a la influencia mutua de las dos partículas, la partícula alfa (Z=2) y el núcleo resultante de la desintegración radioactiva (Z_D=Z-2)

$d=4^{1/3}+A_D^{1/3}$ es la distancia entre el núcleo resultante y el centro de la partícula alfa, A_D=A-4, que es la suma de los dos radios. La figura, representa el potencial V(r)

${\displaystyle V(r)=\{\begin{array}{l}-V_0,r\le d\\ \frac{1}{4\pi {\epsilon }_0}\frac{2Z_D{e}^2}{r},r>d\end{array}}$

-V₀ es la energía potencial constante en el interior del núcleo y b es la distancia a la que V(r)=E. Siendo E la energía de la partícula alfa

${\displaystyle \frac{1}{4\pi {\epsilon }_0}\frac{2Z_D{e}^2}{b}=E}$

La energía cinética de la partícula alfa en el interior del núcleo radioactivo es E+V₀

Fórmula del coeficiente de transmisión

Deducimos la expresión analítica aproximada del coeficiente de transmisión para un potencial V(x), que en la página titulada Barrera de potencial de forma cualesquiera calculamos mediante procedimientos numéricos

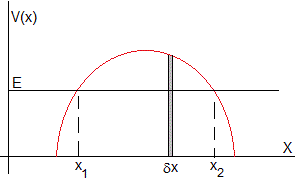
Hemos visto que la función de onda en la barrera de potencial es, Ψ₂(x)=Cexp(qx)+Dexp(-qx), q^2=\frac{2m\left(V_0-E\right)}{{\hslash }^2} . Comprobamos que el coeficiente C es pequeño comparado con D, por lo que la función de onda en esta región es casi una exponencial decreciente con x. Si el potencial V(x) no es constante q y D variarán con x

Sea el potencial V(x) de la figura. Una partícula de masa m tiene una energía E, la función de onda en la posición x+δx se puede aproximar a

${\displaystyle \begin{array}{l}\psi (x+\delta x)=\psi \left(x\right)\exp \left(-q(x)\delta x\right)\\ q^2(x)=\frac{2m\left(V(x)-E\right)}{{\hslash }^2}\end{array}}$

Desarrollamos en serie (hasta el primer término) el miembro izquierdo y derecho

>> syms q x;
>> taylor(exp(-q*x),x,0,'Order',2)
ans =1 - q*x

${\displaystyle \begin{array}{l}\psi (x)+\frac{d\psi (x)}{dx}\delta x\approx \psi (x)\left(1-q(x)·\delta x\right)\\ {\displaystyle \underset{x_1}{\overset{x_2}{\int }}\frac{d\psi }{\psi }}=-{\displaystyle \underset{x_1}{\overset{x_2}{\int }}q(x)·dx}\\ \frac{\psi (x_2)}{\psi (x_1)}\approx \exp \left(-{\displaystyle \underset{x_1}{\overset{x_2}{\int }}q(x)·dx}\right)\end{array}}$

El coeficiente de transmisión T es

${\displaystyle T={\left|\frac{\psi (x_2)}{\psi (x_1)}\right|}^2\approx \exp \left(-2\frac{\sqrt{2m}}{\hslash }{\displaystyle \underset{x_1}{\overset{x_2}{\int }}\sqrt{V(x)-E}·dx}\right)}$

Constante de desintegración

Con esta fórmula, calculamos el coeficiente de transmisón para nuestro modelo de desintegración alfa, teniendo en cuenta que la masa m se corresponde con la masa reducida del sistema formado por la partícula alfa (A=4) y el núcleo resultante de la desintegración (A_D=A-4)

${\displaystyle \mu =\frac{4m_D}{4+m_D}=\frac{4A_D}{4+A_D}}$

El coeficiente de transmisión T es

${\displaystyle \begin{array}{l}T=\exp \left(-2\frac{\sqrt{2\mu }}{\hslash }{\displaystyle \underset{d}{\overset{b}{\int }}\sqrt{\frac{1}{4\pi {\epsilon }_0}\frac{2Z_D{e}^2}{r}-E}·dr}\right)\\ T=\exp \left(-2\frac{\sqrt{2\mu E}}{\hslash }{\displaystyle \underset{d}{\overset{b}{\int }}\sqrt{\left(\frac{b}{r}-1\right)}·dr}\right)\end{array}}$

Para resolver la integral hacemos el cambio de variable r=bcos²θ, dr=-2bsinθ·cosθ·dθ

${\displaystyle \begin{array}{l}{\displaystyle \int \sqrt{\frac{b}{r}-1}·dr=-{\displaystyle \int 2b{\sin }^2\theta ·d\theta }}=-b{\displaystyle \int \left(1-\cos 2\theta \right)d\theta }-b\left(\theta -\frac{1}{2}\sin 2\theta \right)\\ =-b\left(\theta -\sin \theta ·\cos \theta \right)=-b\left(\arccos \sqrt{\frac{r}{b}}-\sqrt{\frac{r}{b}}\sqrt{1-\frac{r}{b}}\right)\end{array}}$

La integral definida vale

${\displaystyle \begin{array}{l}{\displaystyle \underset{d}{\overset{b}{\int }}\sqrt{\left(\frac{b}{r}-1\right)}·dr}={b\left(\arccos \sqrt{\frac{r}{b}}-\sqrt{\frac{r}{b}}\sqrt{1-\frac{r}{b}}\right)|}_b^d=\\ b\left(\arccos \sqrt{\frac{d}{b}}-\sqrt{\frac{d}{b}}\sqrt{1-\frac{d}{b}}\right)\end{array}}$

El coeficiente de transmisión es

${\displaystyle T=\exp \left(-2\frac{b\sqrt{2\mu E}}{\hslash }\left(\arccos \left(\sqrt{\frac{d}{b}}\right)-\sqrt{\frac{d}{b}}\sqrt{1-\frac{d}{b}}\right)\right)}$

La constante de desintegración λ y la vida media τ (en la siguiente sección titulada 'Desintegración radioactiva' se define esta propiedad) son

${\displaystyle \begin{array}{l}\lambda =\frac{vT}{2R_0},\tau =\frac{\ln 2}{\lambda }\\ \ln \lambda =\ln \frac{v}{2R_0}-2\frac{b\sqrt{2\mu E}}{\hslash }\left(\arccos \sqrt{\frac{d}{b}}-\sqrt{\frac{d}{b}}\sqrt{1-\frac{d}{b}}\right)\end{array}}$

Ejemplo

Calculamos la vida media τ de un isótopo de torio, A=234, Z=90. La energía de la partícula alfa es E=4.2 MeV. En la primera referencia, no se proporciona el dato del potencial V₀, necesario para calcular la velocidad de las partículas alfa en el interior del núcleo sin desintegrar (quizás no se tiene en cuenta por ser próximo a cero). Despreciando efectos relativistas que seguramente hay que tener en cuenta

${\displaystyle v=\sqrt{\frac{2\left(E+V_0\right)}{m}}}$

Donde m es la masa de la partícula alfa

e=1.6021e-19;% carga elemental
h=1.0545e-34; %constante h/2pi
A=234; %isótopo radioactivo de torio
Z=90;
A_D=A-4; %núcleo resultante de la desintegración
mu=4*A_D*1.66e-27/(4+A_D); %masa reducida 
d=1.4e-15*(4^(1/3)+A_D^(1/3)); %distancia núcleo resultante - p. alfa
E=4.2*1e6*e; %energía de la partícula alfa, 4.2 MeV
b=9e9*2*(Z-2)*e^2/E;
%coef. transmisión
T=exp(-2*b*sqrt(2*mu*E)*(acos(sqrt(d/b))-sqrt(d/b)*sqrt(1-d/b))/h);
m=4*1.66e-27; %masa de la partícula alfa
V0=0; %potencial dentro del núcleo (no se dispone del dato)
v=sqrt(2*(E+V0)/m); %velocidad de la partícula alfa dentro del núcleo
R_0=1.4e-15*A^(1/3);%radio del núcleo sin desintegrar
lambda=v*T/(2*R_0); %constante de desintegración
t_medio=log(2)/lambda; %vida media
disp(t_medio)

El resultado es τ=9.1·10¹³ s. Este resultado difiere del proporcionado en la primera referencia, primera fila de la tabla 1

  9.1238e+13

La desintegración radioactiva

Los núcleos están compuestos por protones y neutrones, que se mantienen unidos por la denominada fuerza fuerte. Algunos núcleos tienen una combinación de protones y neutrones que no conducen a una configuración estable. Estos núcleos son inestables o radiactivos. Los núcleos inestables tienden a aproximarse a la configuración estable emitiendo ciertas partículas. Los tipos de desintegración radiactiva se clasifican de acuerdo a la clase de partículas emitidas.

Desintegración alfa: El elemento radiactivo de número atómico Z, emite un núcleo de Helio (dos protones y dos neutrones), el número atómico disminuye en dos unidades y el número másico en cuatro unidades, produciéndose un nuevo elemento situado en el lugar Z-2 de la Tabla Periódica.

Desintegración beta: El núcleo del elemento radiactivo emite un electrón, en consecuencia, su número atómico aumenta en una unidad, pero el número másico no se altera. El nuevo elemento producido se encuentra el lugar Z+1 de la Tabla Periódica.

Desintegración gamma: El núcleo del elemento radiactivo emite un fotón de alta energía, la masa y el número atómico no cambian, solamente ocurre un reajuste de los niveles de energía ocupados por los nucleones.

El programa interactivo describe un modelo de sustancia radiactiva A que se desintegra en una sustancia estable B. Se disponen N núcleos radiactivos de la sustancia inestable A. Se introduce la constante de desintegración λ. A medida que transcurre el tiempo se anota el número de núcleos que permanecen sin desintegrar. Posteriormente, se comprobará la ley exponencial decreciente a partir de los datos tomados.

De la observación del proceso de desintegración podemos extraer las siguientes relaciones cualitativas:

• La velocidad de desintegración decrece a medida que los núcleos radiactivos se van desintegrando.
• No podemos predecir en que instante se desintegrará un núcleo concreto, ni qué núcleo se va a desintegrar en un determinado instante.

Se ha observado que todos los procesos radiactivos simples siguen una ley exponencial decreciente. Si N₀ es el número de núcleos radiactivos en el instante inicial, después de un cierto tiempo t, el número de núcleos radiactivos presentes N se ha reducido a

N=N₀exp(-λt)

donde λ es una característica de la sustancia radiactiva denominada constante de desintegración.

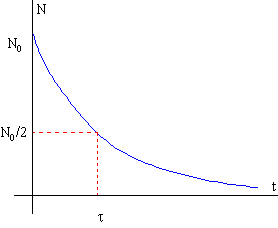
Para cada sustancia radiactiva hay un intervalo τ fijo, denominado vida media, durante el cual el número de núcleos que había al comienzo se reduce a la mitad. Poniendo en la ecuación N=N₀/2 se obtiene

${\displaystyle \tau =\frac{\ln 2}{\lambda }}$

que relaciona la vida media y la constante de desintegración.

El modelo simple de núcleo radioactivo estudado en el primer apartado nos ha permitido conocer el significado de la constante de desintegración.

La ley de desintegración puede deducirse del siguiente modo: si λ es la probabilidad de desintegración por unidad de tiempo, la probabilidad de que un núcleo se desintegre en un tiempo dt es λ·dt. Si hay N núcleos presentes, en el tiempo dt podemos esperar que se desintegren (λ dt)N núcleos

dN=-(λdt)N

El signo menos aparece por que N disminuye con el tiempo a consecuencia de la desintegración. Integrando esta ecuación obtenemos la ley exponencial decreciente.

${\displaystyle {\displaystyle \underset{N_0}{\overset{N}{\int }}\frac{dN}{N}}={\displaystyle \underset{0}{\overset{t}{\int }}-\lambda dt}N=N_0\exp (-\lambda t)}$

N₀ es el número inicial de núcleos radioactivos presentes en el instante t=0.

Fenómenos análogos

Un fenómeno análogo a la desintegración radioactiva es la descarga de un condensador a través de una resistencia, y la descarga de un tubo que contiene fluido viscoso a través de un capilar.

Un fenómeno análogo a la carga de un condensador es la producción y posterior desintegración de núcleos radioactivos en un reactor nuclear. El fenómeno análogo en fluidos es la carga y descarga de un tubo-capilar.

Disponiendo varios tubos-capilares uno encima del otro, de modo que el superior descargue en el inferior y el último, en un tubo cerrado estudiamos el comportamiento de una serie de desintegración radioactiva.

Actividades

• Se introduce la constante de desintegración, en el control titulado Constante, un valor mayor que cero pero menor que 1.
• Se pulsa en el botón Nuevo para comenzar el proceso de desintegración. El núcleo de color azul al desintegrarse se transforma en el núcleo estable de color rojo.

Análisis de los datos

Datos tomados de la experiencia simulada: en el eje X el tiempo en segundos, en el eje Y, el número de átomos sin desintegrar .

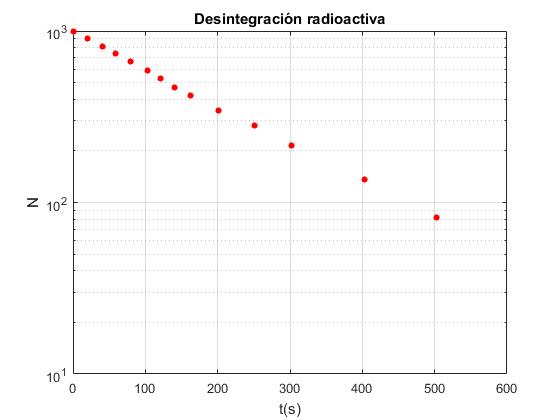
Representamos los datos en un gráfico semilogarítmico

x=[0,19.7,41,59.3,79.8,102.6,120.9,141,162.5,201.4,251.4,301.9,403.4,502.1];
y=[1000,904,812,740,665,588,532,470,421,343,283,215,137,82];
semilogy(x,y,'ro','markersize',4,'markerfacecolor','r')
grid on
xlabel('t(s)')
ylabel('N')
title('Desintegración radioactiva')

Alternativamente, en un gráfico normal representamos log(N) en el eje Y

x=[0,19.7,41,59.3,79.8,102.6,120.9,141,162.5,201.4,251.4,301.9,403.4,502.1];
y=[1000,904,812,740,665,588,532,470,421,343,283,215,137,82];
plot(x,log(y),'ro','markersize',4,'markerfacecolor','r')
grid on
xlabel('t(s)')
ylabel('N')
title('Desintegración radioactiva')

Seleccionamos en el menú Tools/Basic Fitting, y activamos la casilla linear (polinomio de grado 1) en el primer panel titulado Plot fits. Observamos en la ventana Figure 1 la recta que mejor ajusta a los datos experimentales. La ecuación de dicha recta se muestra en la ventana gráfica, activando la casilla Show equations.

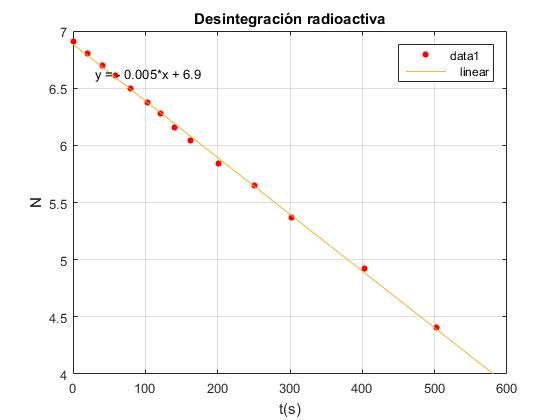
Ampliamos el cuadro de diálogo pulsando en el botón con la flecha inferior derecha -->. Seleccionamos en el segundo panel titulado Numerical results Fit/linear y nos aparece

y = p1*x + p2 

Coefficients:
  p1 = -0.0049633
  p2 = 6.8855

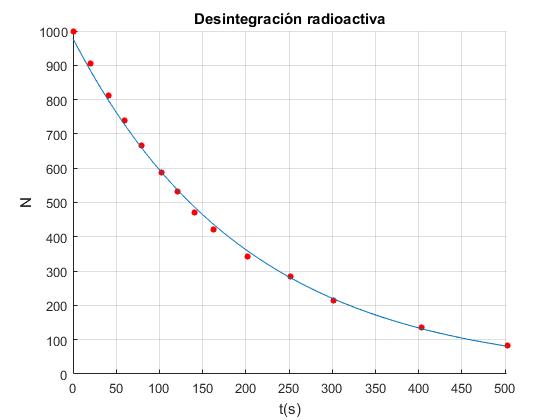
Finalmente, representamos los datos experimentales y curva exponencial decreciente que ajusta a los datos

x=[0,19.7,41,59.3,79.8,102.6,120.9,141,162.5,201.4,251.4,301.9,403.4,502.1];
y=[1000,904,812,740,665,588,532,470,421,343,283,215,137,82];
hold on
plot(x,y,'ro','markersize',4,'markerfacecolor','r')
z=@(t) exp(6.8855)*exp(-0.0049633*t);
fplot(z,[x(1),x(end)])
grid on
xlabel('t(s)')
ylabel('N')
title('Desintegración radioactiva')

Referencias

Mohamed E. Kelabi. Half-life of Alpha Decay from A Straight-line Potential Barrier

Yung-Kuo Lim. Problems and Solutions on Atomic, Nuclear and Particle Physics. World Scientific. (2000). Problem 2033, pp. 249-251