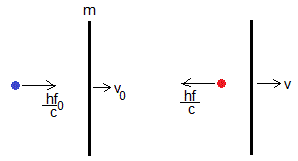
Supongamos que un fotón de energía E=hf₀ y momento lineal p=hf₀/c choca normalmente a un espejo perfectamente reflectante de masa m y que se mueve con velocidad v₀.

La conservación del momento lineal y de la energía se escriben

${\displaystyle \{\begin{array}{l}m{v}_0+\frac{h{f}_0}{c}=-\frac{hf}{c}+mv\\ \frac{1}{2}m{v}_0^2+h{f}_0=\frac{1}{2}m{v}^2+hf\end{array}}$

En este sistema de dos ecuaciones,

${\displaystyle \begin{array}{l}\{\begin{array}{l}m\left(v^2-v_0^2\right)=2h\left(f_0-f\right)\\ m(v-v_0)=\frac{h}{c}\left(f_0+f\right)\end{array}\\ \frac{v+v_0}{2c}=\frac{f_0-f}{f_0+f}\end{array}}$

Para pequeños cambios en la frecuencia y velocidad v+v₀≈2v₀, f+f₀≈2f₀. La variación de frecuencia Δf=f-f₀ es

${\displaystyle \frac{\Delta f}{f_0}\approx -\frac{v_0}{2c}}$

Efector Doppler

Un espejo móvil perfectamente refectante se mueve con velocidad constante v. Un rayo de luz de longitud de onda λ₀ incide sobre el espejo, formando un ángulo θ₁ con la dirección normal

Sea A y B las posiciones consecutivas de dos frentes de onda separados una longitud de onda λ₀. El frente de onda en la posición B se refleja en el espejo móvil en el instante t₀. El frente de onda en A tiene que viajar una distancia c(t-t₀) antes de reflejase en el espejo. La reflexión ocurre en el punto A' en el instante t cuando el espejo se ha desplazado desde B hasta C una distancia v(t-t₀), desde su posición inicial en el instante t₀.

${\displaystyle \begin{array}{l}\overline{\text{AA'}}=\overline{\text{AB}}+\overline{\text{BA'}}\\ \overline{\text{BA'}}=c(t-t_0)-{\lambda }_0\end{array}}$

En el mismo intervalo de tiempo, t-t₀, el frente de onda reflejado en B habrá avanzado hasta el punto B', de modo que la distancia de B a B' es c(t-t₀).

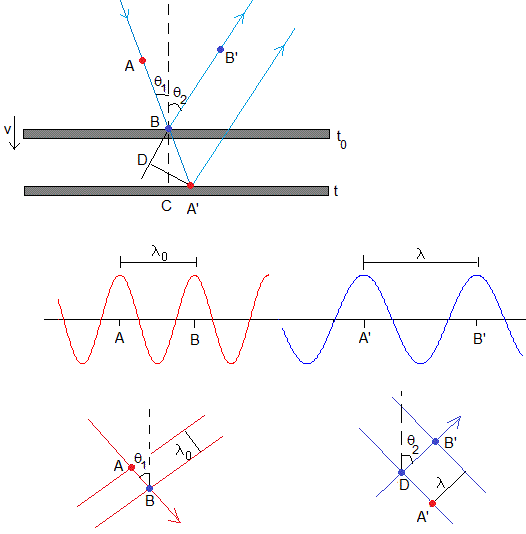
La longitud de onda de la luz reflejada será la distancia entre los puntos A' y B' o bien, la distancia entre D (proyección de A') y B' tal como se muestra en las figuras.

${\displaystyle \begin{array}{l}\overline{\text{DB'}}=\overline{\text{DB}}+\overline{\text{BB'}}\\ \overline{\text{DB}}=\lambda -c(t-t_0)\end{array}}$

Para relacionar las longitudes de la onda electromagnética incidente λ₀ y reflejada λ, examinamos los dos triángulos de la figura ampliada

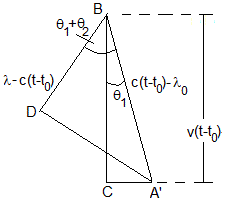
• Triángulo BCA'

${\displaystyle \begin{array}{l}\overline{\text{BA'}}=\frac{\overline{\text{BC}}}{\cos {\theta }_1}=\frac{v(t-t_0)}{\cos {\theta }_1}\\ c(t-t_0)-{\lambda }_0=\frac{v(t-t_0)}{\cos {\theta }_1}\end{array}}$

• Triángulo BDA'

${\displaystyle \begin{array}{l}\overline{\text{DB}}=\overline{\text{BA'}}\cos \left({\theta }_1+{\theta }_2\right)=\frac{v(t-t_0)}{\cos {\theta }_1}\cos \left({\theta }_1+{\theta }_2\right)\\ \lambda -c(t-t_0)=\frac{v(t-t_0)}{\cos {\theta }_1}\cos \left({\theta }_1+{\theta }_2\right)\end{array}}$

Despejando (t-t₀) en la primera ecuación y sustituyendo en la segunda

${\displaystyle t-t_0=\frac{{\lambda }_0}{c-\frac{v}{\cos {\theta }_1}}}$

Queda la ecuación

${\displaystyle \begin{array}{l}\frac{\lambda }{{\lambda }_0}=\frac{c·\cos {\theta }_1+v\cos \left({\theta }_1+{\theta }_2\right)}{c·\cos {\theta }_1-v}\\ \frac{\lambda }{{\lambda }_0}=\frac{c·\cos {\theta }_1+v\left(\cos {\theta }_1\cos {\theta }_2-\sin {\theta }_1\sin {\theta }_2\right)}{c·\cos {\theta }_1-v}\end{array}}$

Utilizamos la relación entre el ángulo de incidencia θ₁ y de reflexión θ₂. Conocemos cosθ₂

${\displaystyle \cos {\theta }_2=\frac{\left(1+\frac{v^2}{c^2}\right)\cos {\theta }_1-2\frac{v}{c}}{1+\frac{v^2}{c^2}-2\frac{v}{c}\cos {\theta }_1}}$

y calculamos sinθ₂

${\displaystyle \sin {\theta }_2=\sqrt{1-{\cos }^2{\theta }_2}=\frac{\left(1-\frac{v^2}{c^2}\right)\sin {\theta }_1}{1+\frac{v^2}{c^2}-2\frac{v}{c}\cos {\theta }_1}}$

Introducimos sinθ₂ y cosθ₂ en la expresión de λ/λ₀.

${\displaystyle \frac{\lambda }{{\lambda }_0}=\frac{c\cos {\theta }_1-v+\frac{v^3}{c^2}-\frac{v^2}{c}\cos {\theta }_1}{\left(c·\cos {\theta }_1-v\right)\left(1+\frac{v^2}{c^2}-2\frac{v}{c}\cos {\theta }_1\right)}}$

Simplificamos

${\displaystyle \frac{\lambda }{{\lambda }_0}=\frac{1-\frac{v^2}{c^2}}{1+\frac{v^2}{c^2}-2\frac{v}{c}\cos {\theta }_1}}$

En términos de la frecuencia de la onda electromagnética incidente λ₀=c/f₀ y reflejada λ=c/f

${\displaystyle f=f_0\frac{1+\frac{v^2}{c^2}-2\frac{v}{c}\cos {\theta }_1}{1-\frac{v^2}{c^2}}}$

En primer lugar, la onda electromagnética no se refleja en el espejo, si la componente vertical de su velocidad, c·cosθ₁ es menor que la velocidad v del espejo, c·cosθ₁<v. El ángulo máximo es cosθ_1m=v/c para el cual f=f₀ no hay cambio en la frecuencia

Representamos el cociente de frecuencias f/f₀ en función del ángulo de incidencia θ₁, para varios valores del cociente v/c positivos (cuando el espejo se aleja de las fuente, la frecuencia disminuye) y negativos (cuando se acerca, la frecuencia aumenta). Cuando v=0, (espejo inmóvil), las frecuencias son iguales f/f₀=1, la representación es una línea recta horizontal

hold on
for k=-0.6:0.3:0.6
    f=@(x) (1+k^2-2*k*cos(x))/(1-k^2);
    if k>0
        fplot(f,[0,acos(k)], 'displayName',num2str(k))
    else
        fplot(f,[0,pi/2], 'displayName',num2str(k))
    end
end
hold off
grid on
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','15','30','45','60','75','90'})
xlabel('\theta_1')
ylabel('f/f_0')
legend('-DynamicLegend','location','northwest')
title('Espejo móvil')

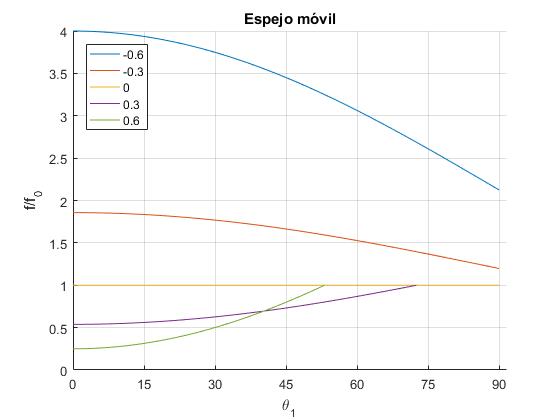
Por ejemplo, para v/c=0.3, θ_1m=72.5° la componente de la velocidad de la onda electromagnética c·cosθ₁ se hace igual a la velocidad v del espejo, no hay cambio de frecuencia f/f₀=1. Véase la línea de color morado marcada con la etiqueta 0.3

Cuando la velocidad del espejo es mucho menor que la velocidad de la luz, v<<c y la incidencia es normal θ₁=0, obtenemos la relación aproximada

${\displaystyle \begin{array}{l}f\approx f_0\left(1-2\frac{v}{c}\right)\\ \frac{\Delta f}{f_0}\approx -\frac{v_0}{2c}\end{array}}$

Referencias

Aleksandar Gjurchinovski. The Doppler effect from a uniformly moving object. Eur. J. Phys. 26 (2005) pp. 643-646

Warren Hirsch, Mark Kobrak. Doppler shift and energy transfer to solar sail. Physics Education, September 2002, pp. 422-423