Transformaciones termodinámicas

Denominamos estado de equilibrio de un sistema cuando las variables macroscópicas presión p, volumen V y temperatura T, no cambian. El estado de equilibrio es dinámico en el sentido de que los constituyentes del sistema se mueven continuamente.

El estado del sistema se representa por un punto en un diagrama p-V. Podemos llevar al sistema desde un estado inicial a otro final a través de una sucesión de estados de equilibrio.

Se denomina ecuación de estado a la relación que existe entre las variables p, V y T. La ecuación de estado más sencilla es la de un gas ideal pV=nRT, donde n representa el número de moles y R la constante de los gases R=0.082 atm·l/(K·mol)=8.3143 J/(K·mol).

Se denomina energía interna del sistema a la suma de las energías de todas sus partículas. En un gas ideal las moléculas solamente tienen energía cinética, los choques entre las moléculas se suponen perfectamente elásticos, la energía interna solamente depende de la temperatura.

El trabajo total realizado cuando el sistema pasa del estado A cuyo volumen es V_A al estado B cuyo volumen es V_B.

$W = \int_{V_{A}}^{V_{B}} p d V$

Cuando una sustancia incrementa su temperatura de T_A a T_B, el calor absorbido se obtiene multiplicando la masa (o el número de moles n) por el calor específico c y por la diferencia de temperatura T_B-T_A.

Q=nc(T_B-T_A)

Cuando no hay intercambio de energía (en forma de calor) entre dos sistemas, decimos que están en equilibrio térmico. Las moléculas individuales pueden intercambiar energía, pero en promedio, la misma cantidad de energía fluye en ambas direcciones, no habiendo intercambio neto. Para que dos sistemas estén en equilibrio térmico deben de estar a la misma temperatura.

Primera ley de la Termodinámica

La primera ley no es otra cosa que el principio de conservación de la energía aplicado a un sistema de muchísimas partículas. A cada estado del sistema le corresponde una energía interna U. Cuando el sistema pasa del estado A al estado B, su energía interna cambia en

ΔU=U_B-U_A

Supongamos que el sistema está en el estado A y realiza un trabajo W, expandiéndose. Dicho trabajo mecánico da lugar a un cambio (disminución) de la energía interna de sistema

ΔU=-W

Cambiamos el estado del sistema poniéndolo en contacto térmico con otro sistema a diferente temperatura. Si fluye una cantidad de calor Q del segundo al primero, aumenta su energía interna en

ΔU=Q

Si el sistema experimenta una transformación cíclica, el cambio en la energía interna es cero, ya que se parte del estado A y se regresa al mismo estado, ΔU=0. Sin embargo, durante el ciclo el sistema ha efectuado un trabajo, que ha de ser proporcionado por los alrededores en forma de transferencia de calor, para preservar el principio de conservación de la energía, W=Q.

Si la transformación no es cíclica, ΔU≠ 0
Si no se realiza trabajo mecánico, ΔU=Q
Si el sistema está aislado térmicamente, ΔU=-W
Si el sistema realiza trabajo, U disminuye
Si se realiza trabajo sobre el sistema, U aumenta
Si el sistema absorbe calor al ponerlo en contacto térmico con un foco a temperatura superior, U aumenta.
Si el sistema cede calor al ponerlo en contacto térmico con un foco a una temperatura inferior, U disminuye.

Todo estos casos, los resumimos en una única ecuación que describe la conservación de la energía del sistema.

ΔU=Q-W

Si el estado inicial y final están muy próximos entre sí, el primer principio se escribe

dU=dQ-pdV

Transformaciones

La energía interna U del sistema depende únicamente del estado del sistema, en un gas ideal depende solamente de su temperatura. Mientras que la transferencia de calor o el trabajo mecánico dependen del tipo de transformación o camino seguido para ir del estado inicial al final.

Isócora o a volumen constante

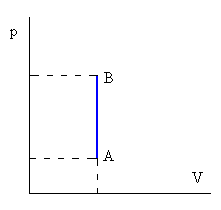
No hay variación de volumen del gas, luego

W=0

Q=nc_V(T_B-T_A)

Donde c_V es el calor específico a volumen constante

Isóbara o a presión constante

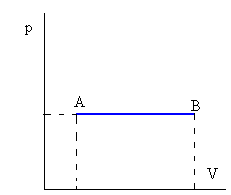
W=p(V_B-V_A)

Q=nc_P(T_B-T_A)

Donde c_P es el calor específico a presión constante

Calores específicos a presión constante c_P y a volumen constante c_V

En una transformación a volumen constante, dU=dQ=nc_VdT

En una transformación a presión constante, dU=nc_PdT-pdV

Como la variación de energía interna dU no depende del tipo de transformación, sino solamente del estado inicial y del estado final, la segunda ecuación se puede escribir como nc_VdT=nc_PdT-pdV

Empleando la ecuación de estado de un gas ideal pV=nRT, obtenemos la relación entre los calores específicos a presión constante y a volumen constante

c_V=c_P-R

Para un gas monoatómico $U = \frac{3}{2} n R T c_{V} = \frac{3}{2} R c_{P} = \frac{5}{2} R$

Para un gas diatómico $U = \frac{5}{2} n R T c_{V} = \frac{5}{2} R c_{P} = \frac{7}{2} R$

La variación de energía interna en un proceso AB es ΔU=nc_V(T_B-T_A)

Se denomina índice adiabático de un gas ideal al cociente $γ = \frac{c_{P}}{c_{V}}$

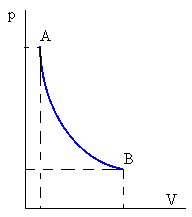
Isoterma o a temperatura constante

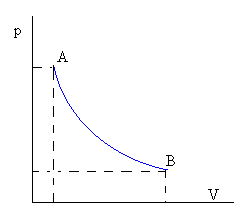
pV=nRT

La curva p=cte/V que representa la transformación en un diagrama p-V es una hipérbola cuyas asíntotas son los ejes coordenados.

$W = \int_{V_{A}}^{V_{B}} p d V = \int_{V_{A}}^{V_{B}} \frac{n R T}{V} d V = n R T \ln \frac{V_{B}}{V_{A}}$

ΔU=0

Q=W

Adiabática o aislada térmicamente, Q=0

Ecuación de la transformación adiabática

Del primer principio dU=-pdV

$n c_{V} d T = - \frac{n R T}{V} d V \frac{d T}{T} = - \frac{R}{c_{V}} \frac{d V}{V}$

Integrando

$\ln T = \frac{R}{c_{V}} \ln V + cte T V^{R / c_{V}} = cte P V^{R / c_{V} + 1} = cte$

Donde el exponente de V se denomina índice adiabático γ del gas ideal

$γ = \frac{R}{c_{V}} + 1 = \frac{c_{P} - c_{V}}{c_{V}} + 1 = \frac{c_{P}}{c_{V}}$

Si A y B son los estados inicial y final de una transformación adiabática se cumple que

$p_{A} V_{A}^{γ} = p_{B} V_{B}^{γ}, T_{A} V_{A}^{γ - 1} = T_{B} V_{B}^{γ - 1}$

Para calcular el trabajo, es necesario efectuar una integración similar a la transformación isoterma.

$W = \int_{V_{A}}^{V_{B}} p d V = \int_{V_{A}}^{V_{B}} \frac{cte}{V^{γ}} d V = \frac{cte}{- γ + 1} (V_{B}^{- γ + 1} - V_{A}^{- γ + 1}) = \frac{1}{- γ + 1} (p_{B} V_{B} - p_{A} V_{A})$

El trabajo es igual a la variación de energía interna cambiada de signo

Si Q=0, entonces W=-ΔU=-nc_V(T_B-T_A)

Cuadro-resumen de las transformaciones termodinámicas

Ecuación de estado de un gas ideal	pV=nRT
Ecuación de una transformación adiabática	$p V^{γ} = cte$
Relación entre los calores específicos	c_p-c_V=R
Índice adiabático de un gas ideal	$γ = \frac{c_{p}}{c_{V}}$
Primer Principio de la Termodinámica	ΔU=Q-W

Transformación	Calor	Trabajo	Var. Energía Interna
Isócora (v=cte)	Q=nc_V(T_B-T_A)	0	ΔU=nc_V(T_B-T_A)
Isóbara (p=cte)	Q=nc_p(T_B-T_A)	W=p(V_B-V_A)	ΔU=nc_V(T_B-T_A)
Isoterma (T=cte)	Q=W	$W = n R T \ln \frac{V_{B}}{V_{A}}$	ΔU=0
Adibática (Q=0)	0	W=-ΔU	ΔU=nc_V(T_B-T_A)