Conservación de la energía

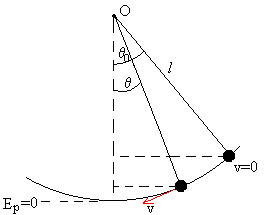
Como hemos visto en la página anterior. El principio de conservación de la energía se expresa

${\displaystyle E=\frac{1}{2}m{\left(l\frac{d\theta }{dt}\right)}^2+mgl\left(1-\cos \theta \right)}$

El máximo desplazamiento angular del péndulo θ₀ se obtiene para dθ/dt=0

E=mgl(1-cosθ₀)

Alcanza la velocidad máxima v_m cuando pasa por el punto más bajo de la trayectoria θ=0

${\displaystyle E=\frac{1}{2}m{v}_m^2}$

Curva de la energía potencial

Las curvas de energía potencial nos suministran información cualitativa acerca del comportamiento del sistema físico.

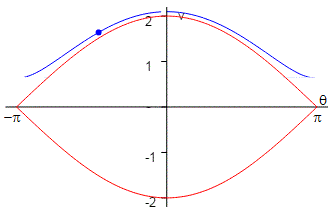
La energía potencial del péndulo es E_p=mgl(1-cosθ). La energía potencial máxima del péndulo es 2mgl, cuando está en posición invertida. Representamos en la parte superior derecha, el cociente de la energía potencial E_p entre la energía potencia máxima, en función del ángulo θ, es decir la función

${\displaystyle e_p=\frac{1}{2}\left(1-\cos \theta \right)}$

En estas unidades, la energía potencial máxima es la unidad para θ=π, cuando el péndulo está invertido (posición de equilibrio inestable) y la mínima (cero) para θ=0, posición de equilibrio estable.

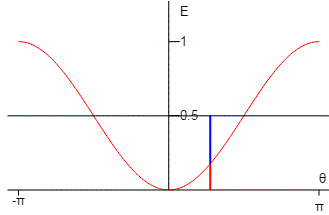
En dicho diagrama, representamos mediante una recta de color negro la energía total E, suma de la energía potencial y de la energía cinética. Un segmento vertical de color rojo, señala la energía potencial del péndulo para la posición θ, y un segmento de color azul, la energía cinética del péndulo en dicha posición. Los valores de la energía total, cinética y potencial se han dividido por la energía potencial máxima 2mgl.

El principio de conservación de la energía establece que la suma de la energía cinética y la energía potencial es constante. De modo que, la energía cinética es máxima cuando la energía potencial es mínima (cuando el péndulo pasa por la posición de equilibrio estable) y la energía cinética es mínima (cero) cuando el péndulo alcanza la desviación máxima.

El espacio de las fases

En el diagrama de fases, representamos la velocidad angular dθ/dt en función del desplazamiento angular θ.

Si el movimiento de un sistema físico es periódico el sistema vuelve al mismo estado después de un ciclo completo. La representación de su trayectoria en el espacio de las fases es una curva cerrada.

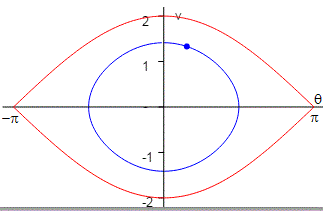
Observamos que la trayectoria en el espacio de las fases es simétrica respecto del eje vertical (de la velocidad angular). Esta simetría quiere decir, que el movimiento del péndulo es el mismo en el sentido de las agujas del reloj que en sentido contrario. Pueden ocurrir dos casos:

Oscilaciones

Que la energía total E del péndulo sea menor que el máximo valor de la energía potencia (E<2mgl) o bien (e<1). En el diagrama de la energía potencial vemos que la energía total es menor que la altura de la barrera de potencial. El péndulo oscila entre dos posiciones extremas θ₀ y -θ₀.

Si la amplitud es pequeña, el péndulo describe un Movimiento Armónico Simple y la trayectoria en el espacio de las fases se aproxima a una elipse.

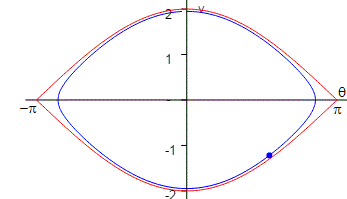
A medida que se aumenta la energía, la trayectoria en el espacio de las fases se desvía de la forma elíptica y la oscilación deja de ser armónica. Como el péndulo pasa mucho más tiempo en las proximidades de su desviación máxima θ₀, la trayectoria en el espacio de las fases se hace más aguda en los extremos izquierdo y derecho, y más plana en la parte superior e inferior.

Rotaciones

Cuando la energía total E del péndulo es mayor que el máximo valor de la energía potencial (E>2mgl) o bien (e>1), el péndulo da vueltas completas.

El movimiento de rotación no es uniforme, la velocidad es máxima cuando pasa por la posición de equilibrio estable y es mínima cuando pasa por la posición de péndulo invertido. La posición angular del péndulo se incrementa continuamente y la velocidad angular es siempre positiva (si la rotación es en sentido contrario a las agujas del reloj).

El péndulo repite el mismo movimiento cuando su posición angular θ se incrementa en 2π , 4π , etc. Para describir este movimiento en el espacio de las fases, es suficiente con considerar la parte de dicho espacio comprendida entre -π y π . El punto que representa la posición y la velocidad angular del péndulo en el espacio de las fases sale de dicha región por la derecha y entra por la izquierda.

Trayectoria separatriz

Cuando la energía total del péndulo E=2mgl, (e=1) estamos en el caso límite. La trayectoria del punto representativo en el espacio de las fases está señalada en color rojo y se denomina separatriz.

Poniendo E=2mgl en el principio de conservación de la energía, obtenemos la ecuación de la separatriz

${\displaystyle \begin{array}{l}2mgl=\frac{1}{2}m{\left(l\frac{d\theta }{dt}\right)}^2+mgl\left(1-\cos \theta \right)\\ \left(\frac{d\theta }{dt}\right)=2\sqrt{\frac{g}{l}}\cos \left(\frac{\theta }{2}\right)\end{array}}$

La separatriz divide al espacio de las fases en regiones que corresponden a dos tipos distintos de movimiento.

Cuando el péndulo alcanza la posición θ=-π o θ=π, su velocidad angular dθ/dt=0, el péndulo se encuentra en un estado de equilibrio inestable, en la denominada posición invertida. Un pequeño desplazamiento en uno u otro sentido hace que el péndulo oscile con una amplitud muy próxima a π . Y un pequeño empuje hace que describa un movimiento de rotación.

Actividades

Se introduce el valor de la energía total e en el control de edición titulado Energía. Este valor es el cociente entre la energía total del péndulo E y la energía potencial máxima 2mgl.

Se pulsa el botón titulado Nuevo.

Se observa el movimiento del punto representativo en el espacio de las fases y la forma de la trayectoria que describe.

En la parte superior derecha, observamos cómo cambia la energía cinética (línea gruesa de color azul) y la energía potencial (en color rojo) con la posición θ del péndulo.

En la parte superior izquierda, se proporciona el valor del tiempo t, la posición angular θ y la velocidad angular dθ/dt

Oscilaciones

En este apartado, vamos a examinar el comportamiento del péndulo cuando su energía E<2mgl y por tanto, describe oscilaciones de amplitud 0<θ₀<π

Aplicamos el principio de conservación de la energía. Véase la primera figura de esta página

En la posición extrema θ=θ₀, la energía es solamente potencial.

E=mg(l-lcosθ)

En la posición θ, la energía del péndulo es parte cinética y la otra parte potencial

${\displaystyle E=\frac{1}{2}m{\left(l\frac{d\theta }{dt}\right)}^2+mgl\left(1-\cos \theta \right)}$

La conservación de la energía se escribe

${\displaystyle \begin{array}{l}mgl(1-\cos {\theta }_0)=\frac{1}{2}m{\left(l\frac{d\theta }{dt}\right)}^2+mgl\left(1-\cos \theta \right)\\ {\left(\frac{d\theta }{dt}\right)}^2=\frac{4g}{l}\left({\sin }^2\frac{{\theta }_0}{2}-{\sin }^2\frac{\theta }{2}\right)\end{array}}$

Se ha utilizado la relación trigonométrica, cosθ=cos²(θ/2)-sin²(θ/2)=1-2·sin²(θ/2). Despejando el tiempo dt en la ecuación diferencial

${\displaystyle 2\sqrt{\frac{g}{l}}t={\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{d\theta \text{'}}{\sqrt{{\sin }^2\left(\frac{{\theta }_0}{2}\right)-{\sin }^2\left(\frac{\theta \text{'}}{2}\right)}}}}$

Se hace el cambio de variable

${\displaystyle \begin{array}{l}\sin \left(\frac{\theta }{2}\right)=\sin \phi ·\sin \left(\frac{{\theta }_0}{2}\right)\\ \frac{1}{2}\cos \left(\frac{\theta }{2}\right)d\theta =\sin \left(\frac{{\theta }_0}{2}\right)·\cos \phi ·d\phi \end{array}}$

La integral se expresa

${\displaystyle \begin{array}{l}\sqrt{\frac{g}{l}}t={\displaystyle \underset{0}{\overset{\phi }{\int }}\frac{d\phi \text{'}}{\sqrt{1-{\sin }^2\left(\frac{{\theta }_0}{2}\right){\sin }^2\phi \text{'}}}}\\ 2\pi \tau ={\displaystyle \underset{0}{\overset{\phi }{\int }}\frac{d\phi \text{'}}{\sqrt{1-k^2{\sin }^2\phi \text{'}}}}\\ 2\pi \tau =F(\phi ,k)\end{array}}$

Donde τ=t/P₀, siendo P₀ el periodo del péndulo para pequeñas amplitudes. Con

${\displaystyle \sin \phi =\frac{1}{k}\sin \frac{\theta }{2}k=\sin \frac{{\theta }_0}{2}}$

El resultado de la integral es u=2πτ. Despejamos la posición angular θ en función del tiempo τ del siguiente modo

${\displaystyle \begin{array}{l}\text{sn}u=\sin \phi \\ \text{sn}u=\frac{1}{k}\sin \frac{\theta }{2}\\ \theta =2\arcsin \left(k·\text{sn}(2\pi \tau ,k)\right)\end{array}}$

sn es una función elíptica de Jacobi,

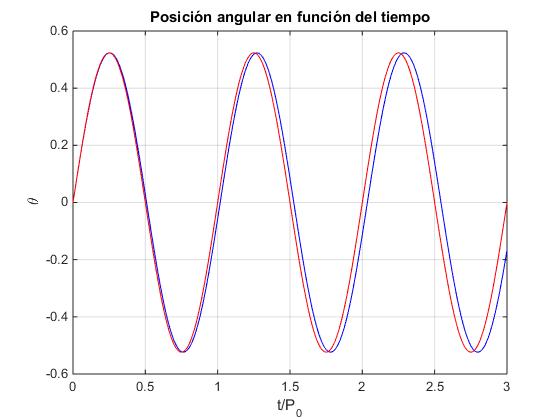
Representamos en color azul la posición angular θ en función del tiempo τ=t/P₀ y la comparamos con la aproximación de las oscilaciones de pequeña amplitud θ=θ₀·sin(2π·τ) en color rojo. La amplitud es θ₀=π/6 (30°).

ang=pi/6; %30°
k=sin(ang/2);
t=0:0.01:3; 
x=2*asin(k*ellipj(2*pi*t,k^2));
xx=ang*sin(2*pi*t);
plot(t,x,'b',t,xx,'r');
xlabel('t/P_0')
ylabel('\theta')
title('Posición angular en función del tiempo')
grid on

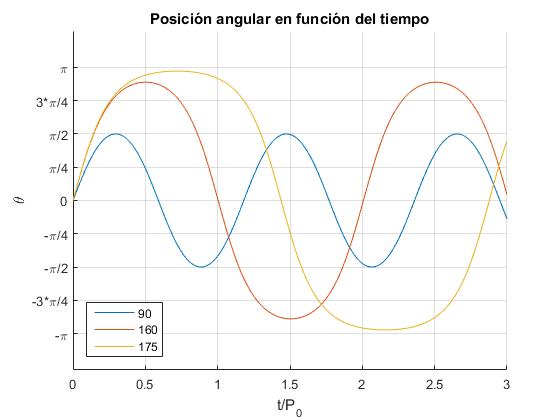
Representamos el desplazamiento θ en función del tiempo τ=t/P₀ para las siguientes amplitudes θ₀=90°, θ₀=160°, θ₀=175°

hold on
for ang=[90,160, 175]
    k=sin(ang*pi/(2*180));
    t=0:0.01:3; 
    x=2*asin(k*ellipj(2*pi*t,k^2));
    plot(t,x, 'displayName',num2str(ang));
end
hold off
set(gca,'YTick',-pi:pi/4:pi)
set(gca,'YTickLabel',{'-\pi','-3*\pi/4','-\pi/2','-\pi/4',
'0', '\pi/4', '\pi/2', '3*\pi/4','\pi'})
legend('-DynamicLegend','location','southwest')
xlabel('t/P_0')
ylabel('\theta')
title('Posición angular en función del tiempo')
grid on

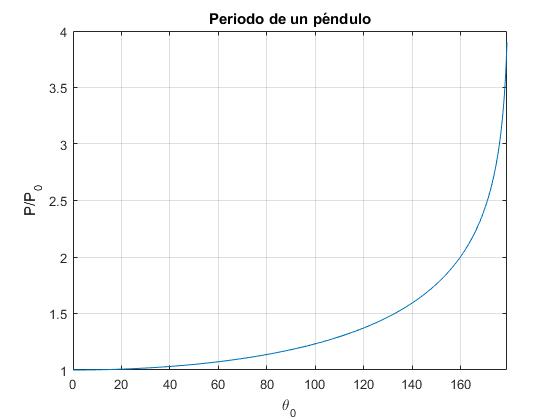
Periodo del péndulo

Cuando θ=θ₀, entonces φ=π/2. El tiempo que tarda el péndulo en ir de θ=0, a θ=θ₀ es un cuarto de periodo.

${\displaystyle \sqrt{\frac{g}{l}}\frac{P}{4}={\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{d\phi \text{'}}{\sqrt{1-{\sin }^2\left(\frac{{\theta }_0}{2}\right){\sin }^2\phi \text{'}}}}}$

El periodo P/P₀ de una oscilación es

${\displaystyle \begin{array}{l}\frac{P}{P_0}=\frac{2}{\pi }{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{d\phi \text{'}}{\sqrt{1-k^2{\sin }^2\phi \text{'}}}}\\ \frac{P}{P_0}=\frac{2}{\pi }K(k),k=\sin \frac{{\theta }_0}{2}\end{array}}$

La integral se denomina elíptica completa de primera especie.

Representemos el periodo P/P₀ de un péndulo en función de la amplitud θ₀ expresada en grados

P=@(x) ellipke(sin(x*pi/(2*180))^2)*2/pi;
fplot(P,[0,179])
xlabel('\theta_0')
ylabel('P/P_0')
title('Periodo de un péndulo')
grid on

Aproximaciones

Desarrollamos en serie el denominador de la integral elíptica

${\displaystyle {(1-k^2{\sin }^2\phi )}^{-1/2}=1+\frac{1}{2}{k}^2{\sin }^2\phi +\frac{3}{8}{k}^4{\sin }^4\phi +\mathrm{...}}$

En el código, llamamos t al producto k²sin²φ. Obtenemos los tres primeros términos del desarrollo en serie (en orden inverso) con el comando series

>> syms t;
>> series('(1-t^2)^(-1/2)',t)
ans =(3*t^4)/8 + t^2/2 + 1

La integral se convierte en

${\displaystyle {\displaystyle \underset{0}{\overset{\pi /2}{\int }}\left(1+\frac{1}{2}{k}^2{\sin }^2\phi +\frac{3}{8}{k}^4{\sin }^4\phi +\mathrm{...}\right)}d\phi =\frac{\pi }{2}+\frac{1}{2}{k}^2\frac{\pi }{4}+\frac{3}{8}{k}^4\frac{3\pi }{16}+\mathrm{...}}$

>> syms t;
>> int('sin(t)^2',t,0,pi/2)
ans =pi/4 

>> int('sin(t)^4',t,0,pi/2)
ans =(3*pi)/16

>> int('sin(t)^6',t,0,pi/2)
ans =(5*pi)/32

El desarrollo en serie del periodo P es

${\displaystyle P=P_0\left(1+\frac{1}{4}{\sin }^2\frac{{\theta }_0}{2}+\frac{9}{64}{\sin }^4\frac{{\theta }_0}{2}+\mathrm{...}\right)}$          (2)

Si la amplitud es pequeña

${\displaystyle {\sin }^2\left(\frac{{\theta }_0}{2}\right)\approx \frac{{\theta }_0^2}{4}}$

y el periodo es, aproximadamente

${\displaystyle P\approx P_0\left(1+\frac{{\theta }_0^2}{16}\right)}$

Esta es la primera aproximación a la fórmula del periodo de un péndulo. Se conocen varias fórmulas aproximadas del periodo del péndulo para cualquier amplitud.

La conclusión final, es que el periodo P crece con la amplitud θ₀. Mientras que el periodo P₀ es independiente de la amplitud siempre que la amplitud no sea muy grande y se pueda aplicar la aproximación sinθ ≈θ.

Rotaciones

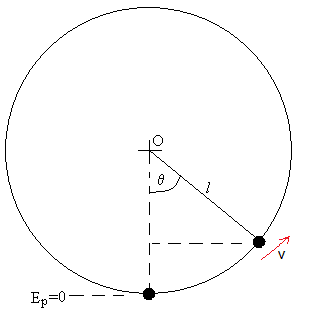
En este caso, la energía E>2mgl. Siendo 2mgl la energía potencial en el punto más alto de la trayectoria circular

En la posición θ, la energía del péndulo es parte cinética y la otra parte potencial

${\displaystyle E=\frac{1}{2}m{\left(l\frac{d\theta }{dt}\right)}^2+mgl\left(1-\cos \theta \right)}$

Integrando, obtenemos el ángulo θ en función del tiempo t

${\displaystyle \begin{array}{l}{\left(\frac{d\theta }{dt}\right)}^2=\frac{2E}{m{l}^2}\left(1-\frac{2mgl}{E}{\sin }^2\left(\frac{\theta }{2}\right)\right)\\ \sqrt{\frac{2E}{m{l}^2}}t={\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{d\theta \text{'}}{\sqrt{1-\frac{2mgl}{E}{\sin }^2\left(\frac{\theta \text{'}}{2}\right)}}}\end{array}}$

Hacemos el cambio de variable φ=θ/2

${\displaystyle \sqrt{\frac{E}{2m{l}^2}}t={\displaystyle \underset{0}{\overset{\theta /2}{\int }}\frac{d\phi }{\sqrt{1-k^2{\sin }^2\phi }}}{k}^2=\frac{2mgl}{E}}$

En términos de τ=t/P₀

${\displaystyle \begin{array}{l}\frac{2\pi }{k}\tau ={\displaystyle \underset{0}{\overset{\theta /2}{\int }}\frac{d\phi }{\sqrt{1-k^2{\sin }^2\phi }}}\\ \frac{2\pi }{k}\tau =F\left(\frac{\theta }{2},k\right)\end{array}}$

Despejamos la posición θ en función del tiempo t, utilizando la función sn de Jacobi

El resultado de la integral es u=2πτ/k. Despejamos la posición angular θ en función del tiempo τ del siguiente modo: sn(u)=sin(θ/2)

${\displaystyle \begin{array}{l}\theta =2\arcsin \left(\text{sn}\left(\frac{2\pi }{k}\tau ,k\right)\right)0\le t\le \frac{P}{2}\\ \theta =2\pi -2\arcsin \left(\text{sn}\left(\frac{2\pi }{k}\tau ,k\right)\right)\frac{P}{2}<t<P\end{array}}$

k=1/1.01;  %v0/vc
P=k*ellipke(k^2)/pi;
t1=0:0.01:P/2; 
x1=2*asin(ellipj(2*pi*t1/k,k^2));
t2=P/2+0.01:0.01:P-0.01;
x2=2*pi-2*asin(ellipj(2*pi*t2/k,k^2));
hold on
plot([t1,t2],[x1,x2])
plot([t1+P,t2+P],[x1,x2])
hold off
xlabel('t/P_0')
ylabel('\theta')
title('Posición angular en función del tiempo')
grid on

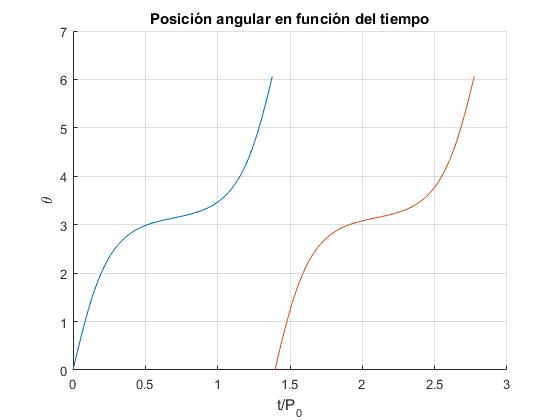
Periodo

El tiempo que tarda el péndulo en desplazarse desde θ=0 a θ=π es la mitad de un periodo P.

${\displaystyle \begin{array}{l}\sqrt{\frac{E}{2m{l}^2}}\frac{P}{2}={\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{d\phi }{\sqrt{1-k^2{\sin }^2\phi }}}\\ \frac{P}{P_0}=\frac{k}{\pi }{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{d\phi }{\sqrt{1-k^2{\sin }^2\phi }}}{k}^2=\frac{2mgl}{E}\end{array}}$

La integral se denomina elíptica completa de primera especie.

Velocidad crítica.

Se denomina velocidad crítica v_c a la velocidad en el punto más bajo de la trayectoria circular para que el péndulo llegue a la posición θ=π de equilibrio inestable (péndulo invertido).

${\displaystyle 2mgl=\frac{1}{2}m{v}_c^2}$

Denominaremos v₀ a la velocidad en el punto más bajo de la trayectoria cuando la energía de la partícula es E.

${\displaystyle E=\frac{1}{2}m{v}_0^2}$

• Para E>2mgl, k=v_c/v₀
• Para E<2mgl, régimen oscilatorio

${\displaystyle \begin{array}{l}E=mgl(1-\cos {\theta }_0)=2mgl{\sin }^2\frac{{\theta }_0}{2}\\ k=\sin \frac{{\theta }_0}{2}=\sqrt{\frac{E}{2mgl}}=\sqrt{\frac{\frac{1}{2}m{v}_0^2}{\frac{1}{2}m{v}_c^2}}=\frac{v_0}{v_c}\end{array}}$

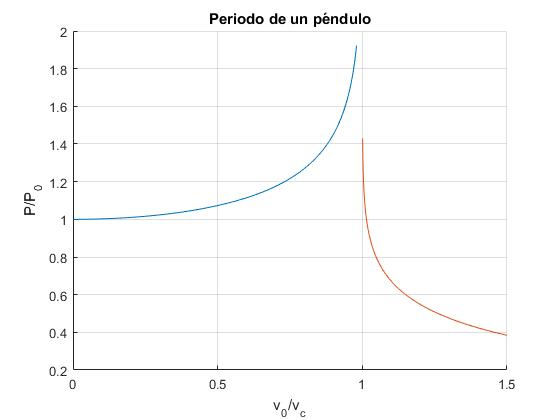
Representemos el periodo P/P₀ de un péndulo en función del cociente v₀/v_c. Distinguiendo dos regiones: v₀/v_c<1 (oscilaciones) y v₀/v_c>1 (rotaciones)

P_1=@(k) ellipke(k^2)*2/pi;
P_2=@(k) ellipke(1/k^2)/(pi*k);
hold on
fplot(P_1,[0,0.98])
fplot(P_2,[1.001,1.5])
hold off
xlim([0,1.5])
xlabel('v_0/v_c')
ylabel('P/P_0')
title('Periodo de un péndulo')
grid on

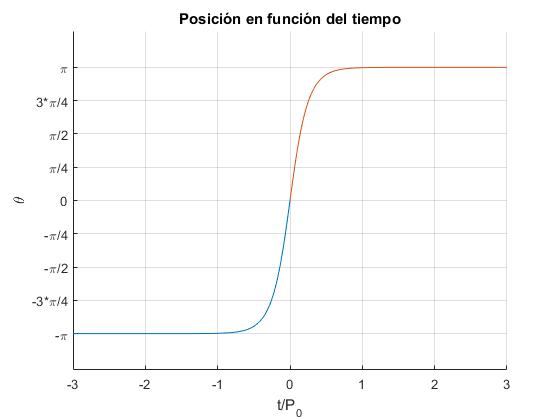
Situación límite

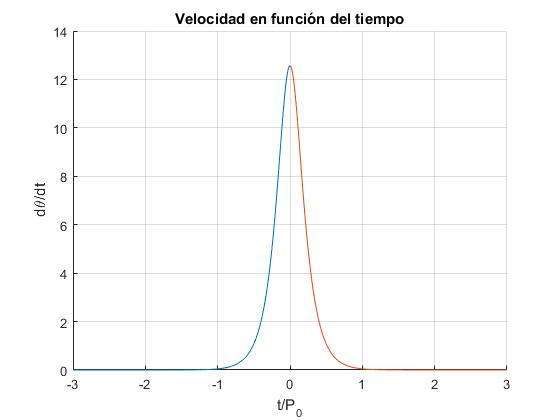
Cuando la energía E del oscilador es igual crítico 2mgl, el péndulo alcanza una posición invertida que es una posición de equilibrio inestable. Si la energía E es un poco mayor que 2mgl, el péndulo experimenta rotaciones y si la energía E del péndulo es un poco menor de 2mgl el péndulo experimenta oscilaciones. Cuando el péndulo alcanza una posición próxima a θ=π, se mueve muy lentamente y tarda un tiempo infinito en alcanzar esta posición

El principio de conservación de la energía con E=2mgl se escribe

${\displaystyle \begin{array}{l}2mgl=\frac{1}{2}m{\left(l\frac{d\theta }{dt}\right)}^2+mgl\left(1-\cos \theta \right)\\ {\left(\frac{d\theta }{dt}\right)}^2=4\frac{g}{l}{\cos }^2\frac{\theta }{2}\end{array}}$

Integrando, obtenemos la posición θ en función del tiempo t.

${\displaystyle 2\sqrt{\frac{g}{l}}t={\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{d\theta }{\cos \frac{\theta }{2}}}}$

Para calcula la integral se hace el cambio x=θ/2 y se utilizan las siguientes relaciones, derivadas del seno y coseno del ángulo doble:

${\displaystyle \begin{array}{l}\cos x=\frac{1-z^2}{1+z^2}z=\tan \frac{x}{2}\\ \sin x=\frac{2z}{1+z^2}\\ dx=\frac{2}{1+z^2}dz\end{array}}$

El integrando es

${\displaystyle \begin{array}{l}2{\displaystyle \int \frac{dx}{\cos x}}=2{\displaystyle \int \frac{2dz}{1-z^2}}=2\log \left(\frac{1+z}{1-z}\right)=2\log \left(\frac{1+\tan (x/2)}{1-\tan (x/2)}\right)=\\ 2\log \left(\frac{1+\tan (\theta /4)}{1-\tan (\theta /4)}\right)\end{array}}$

>> syms t;
>> int('1/cos(t/2)',t)
ans =2*log((sin(t/2) + 1)/cos(t/2))

Evaluamos la integral para los límites 0 y θ

${\displaystyle \begin{array}{l}2\sqrt{\frac{g}{l}}t=2\log \left(\frac{1+\tan (\theta /4)}{1-\tan (\theta /4)}\right)\\ \sqrt{\frac{g}{l}}t=\log \left(\frac{\cos (\theta /4)+\sin (\theta /4)}{\cos (\theta /4)-\sin (\theta /4)}\right)\\ 2\pi \tau =\log \left(\tan \left(\frac{\theta +\pi }{4}\right)\right)\end{array}}$

Donde τ=t/P₀, siendo P₀ el periodo del péndulo para pequeñas amplitudes.

Despejamos el desplazamiento θ en función del tiempo τ.

${\displaystyle \theta =4\text{arctan}\left(\exp (2\pi \tau )\right)-\pi }$

theta_1=@(t) pi-4*atan(exp(-2*pi*t));
theta_2=@(t) 4*atan(exp(2*pi*t))-pi;
hold on
fplot(theta_1,[-3,0])
fplot(theta_2,[0,3])
hold off
xlim([-3,3])
set(gca,'YTick',-pi:pi/4:pi)
set(gca,'YTickLabel',{'-\pi','-3*\pi/4','-\pi/2','-\pi/4',
'0', '\pi/4', '\pi/2', '3*\pi/4','\pi'})
grid on
xlabel('t/P_0')
ylabel('\theta')
title('Posición en función del tiempo')

Derivamos con respecto del tiempo τ, para obtener la velocidad dθ/dτ

${\displaystyle \frac{d\theta }{d\tau }=\frac{8\pi \exp (2\pi \tau )}{1+\exp (4\pi \tau )}=\frac{4\pi }{\cosh (2\pi \tau )}}$

w_1=@(t) 4*pi/cosh(-2*pi*t);
w_2=@(t)  4*pi/cosh(2*pi*t);
hold on
fplot(w_1,[-3,0])
fplot(w_2,[0,3])
hold off
xlim([-3,3])
grid on
xlabel('t/P_0')
ylabel('d\theta/dt')
title('Velocidad en función del tiempo')

Ecuación del movimiento y condiciones iniciales

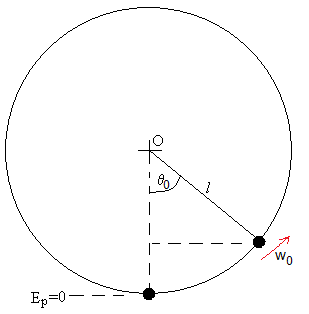
En este apartado, vamos a estudiar con más detalle la ecuación del movimiento del péndulo, cuando en el instante t=0, parte de una posición angular θ₀ con velocidad angular w₀=(dθ/dt)₀

Cuando el péndulo describe oscilaciones de pequeña amplitud, sinθ≈θ. La solución de la ecuación diferencial es

${\displaystyle \theta ={\theta }_0\cos (\omega t)+\frac{w_0}{\omega }\sin (\omega t)}$

Vamos a buscar una solución similar en términos de las funciones elípticas de Jacobi, cualquiera que sean las condiciones iniciales

La conservación de la energía se escribe

${\displaystyle \begin{array}{l}\frac{1}{2}m{\left(l\frac{d\theta }{dt}\right)}^2+mgl(1-\cos \theta )=\frac{1}{2}m{\left(l\frac{d\theta }{dt}\right)}_0^2+mgl(1-\cos {\theta }_0)\\ {\left(\frac{d\theta }{dt}\right)}^2=2{\omega }^2\left(\cos \theta -\cos {\theta }_0\right)+w_0^2\end{array}}$

Despejamos el tiempo t

${\displaystyle \begin{array}{l}\pm t={\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\frac{d\theta }{\sqrt{w_0^2-2{\omega }^2\cos {\theta }_0+2{\omega }^2\cos \theta }}}=\\ {\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{d\theta }{\sqrt{w_0^2-2{\omega }^2\cos {\theta }_0+2{\omega }^2\cos \theta }}}-{\displaystyle \underset{0}{\overset{{\theta }_0}{\int }}\frac{d\theta }{\sqrt{w_0^2-2{\omega }^2\cos {\theta }_0+2{\omega }^2\cos \theta }}}\end{array}}$

En el libro titulado 'Table of Integrals, Series, and Products' buscamos la solución a integrales de este tipo y la encontramos en el apartado 2.571, n° 4 de la página 179

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{d\phi }{\sqrt{a+b\cos \phi }}},\{\begin{array}{l}b=2{\omega }^2\\ a=w_0^2-2{\omega }^2\cos {\theta }_0\end{array}\\ \{\begin{array}{l}\frac{2}{\sqrt{a+b}}F\left(\frac{\theta }{2},r\right),a>b>\mathrm{0,}0\le \theta \le \pi \\ \sqrt{\frac{2}{b}}F\left(\gamma ,\frac{1}{r}\right),b\ge \left|a\right|>\mathrm{0,}0\le \theta <\arccos \left(-\frac{a}{b}\right)\end{array}\\ r=\sqrt{\frac{2b}{a+b}},\gamma =\arcsin \sqrt{\frac{b(1-\cos \theta )}{a+b}}\end{array}}$

La segunda tarea es identificar qué solución corresponde a oscilaciones del péndulo y cuál a rotaciones

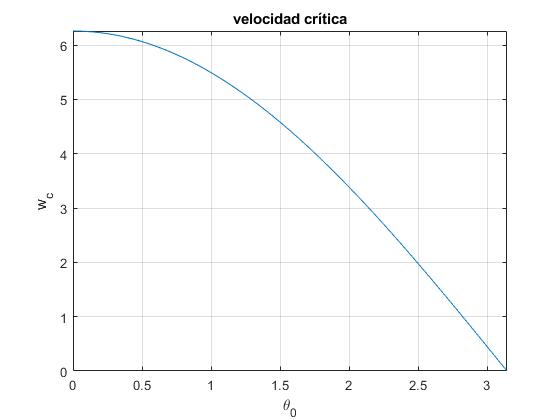
Velocidad angular crítica

Si la energía E es mayor que 2mgl, el péndulo experimenta rotaciones y si la energía E del péndulo es menor de 2mgl el péndulo experimenta oscilaciones.

Supongamos que la posición angular del péndulo es θ₀, vamos a calcular la velocidad angular crítica w_c, para que el péndulo llegue justamente a la posicón final invertida θ=π de equilibrio inestable

${\displaystyle \begin{array}{l}\frac{1}{2}m{l}^2{w}_c^2+mgl(1-\cos {\theta }_0)=2mgl\\ w_c=2\omega \cos \frac{{\theta }_0}{2}\end{array}}$

w=sqrt(9.8);  %sqrt(g/l), l=1 m
f=@(x) 2*w*cos(x/2);
fplot(f,[0,pi])
grid on
xlabel('\theta_0')
ylabel('w_c')
title('velocidad crítica')

Oscilaciones

Se producen cuando la velocidad angular inicial es menor que la crítica, w₀<w_c. El máximo desplazamiento del péndulo se produce cuando dθ/dt=0. En la ecuación de la conservación de la energía despejamos el ángulo θ=θ_m

${\displaystyle \cos {\theta }_m=\cos {\theta }_0-\frac{w_0^2}{2{\omega }^2}}$

que es el cociente -a/b. La segunda solución corresponde a las oscilaciones, ya que en ésta, la posición angular θ<θ_máx

El tiempo t, diferencia de las dos integrales se expresa

${\displaystyle \begin{array}{l}\pm t=\sqrt{\frac{2}{b}}F\left(\gamma ,\frac{1}{r}\right)-\sqrt{\frac{2}{b}}F\left({\gamma }_0,\frac{1}{r}\right)\\ \pm t=\sqrt{\frac{2}{b}}F\left(\gamma ,\frac{1}{r}\right)-t_0\\ \sqrt{\frac{b}{2}}\left(\pm t+t_0\right)=F\left(\gamma ,\frac{1}{r}\right)\end{array}}$

Donde

${\displaystyle \begin{array}{l}\frac{1}{r}=\sqrt{\frac{a+b}{2b}}=\sqrt{\frac{w_0^2-2{\omega }^2\cos {\theta }_0+2{\omega }^2}{4{\omega }^2}}=\sin \frac{{\theta }_m}{2}\\ \gamma =\arcsin \sqrt{\frac{b(1-\cos \theta )}{a+b}}=\arcsin \left(\sqrt{\frac{2b}{a+b}}\sin \frac{\theta }{2}\right)=\arcsin \left(\frac{\sin \frac{\theta }{2}}{\sin \frac{{\theta }_m}{2}}\right)\end{array}}$

Posición angular

Despejamos la posición angular θ en función del tiempo t, utilizando la función elíptica sn de Jacobi

${\displaystyle \begin{array}{l}\sin \gamma =\text{sn}\left(\sqrt{\frac{b}{2}}\left(\pm t+t_0\right),\frac{1}{r}\right)\\ \sin \frac{\theta }{2}\text{=}\sin \frac{{\theta }_m}{2}\text{sn}\left(\omega \left(\pm t+t_0\right),\sin \frac{{\theta }_m}{2}\right)\\ \theta =2\arcsin \left(\sin \frac{{\theta }_m}{2}\text{·sn}\left(\omega \left(\pm t+t_0\right),\sin \frac{{\theta }_m}{2}\right)\right)\end{array}}$

El signo (+) delante de t, se corresponde con una velocidad angular inicial w₀≥0, y el signo (-) con w₀<0

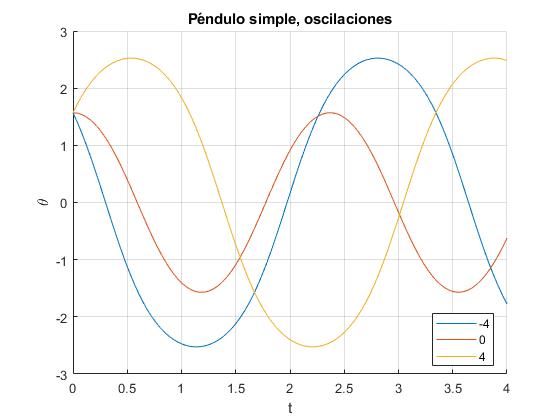
Representamos la posición angular θ en función del tiempo t, para tres velocidades angulares iniciales distintas: w₀=-4, 0, 4 rad/s. La posición angular inicial θ₀=π/2. Para esta posición, la velocidad angular crítica es w_c=4.4272 rad/s. Por tanto, en los tres casos el péndulo oscila

th_0=pi/2; %posición angular inicial
w=sqrt(9.8); %sqrt(g/l), l=1 m
t=linspace(0,4,100);
hold on
for w0=[-4,0,4] %velocidad angular inicial
    th_m=acos(cos(th_0)-w0^2/(2*w^2));
    gamma=asin(sin(th_0/2)/sin(th_m/2));
    t0=ellipticF(gamma,sin(th_m/2)^2)/w;
    signo=1;
    if w0<0
        signo=-1;
    end
    sn=ellipj(w*(signo*t+t0),sin(th_m/2)^2);
    th=2*asin(sn*sin(th_m/2));
    plot(t,th)
end
hold off
grid on
legend('-4','0','4', 'location','best')
xlabel('t')
ylabel('\theta')
title('Péndulo simple, oscilaciones')

Comprobamos que la solución analítica que hemos obtenido, es similar a la solución aplicando procedimientos numéricos

th_0=pi/2; %posición angular inicial
w=sqrt(9.8); %sqrt(g/l), l=1 m
f=@(t,x) [x(2);-w^2*sin(x(1))]; 
hold on
for w0=[-4,0,4] %velocidad angular inicial  
   [t,x]=ode45(f,[0,4],[th_0, w0]);
   plot(t,x(:,1)) %posición angular
end
hold off
grid on
legend('-4','0','4', 'location','best')
xlabel('t')
ylabel('\theta')
title('Péndulo simple, oscilaciones')

Velocidad angular

Dada la posición angular θ(t) respecto del tiempo, derivamos para calcular la velocidad angular, dθ/dt. El lector puede consultar la fórmula de la derivada de la función elíptica de Jacobi, sn(x)

${\displaystyle \begin{array}{l}\theta =2\arcsin (u),u=\sin \frac{{\theta }_m}{2}\text{·sn}\left(\omega \left(\pm t+t_0\right),\sin \frac{{\theta }_m}{2}\right)=\sin \frac{{\theta }_m}{2}·\text{sn}(z)\\ \frac{d\theta }{dt}=2\frac{1}{\sqrt{1-u^2}}\frac{du}{dt}=2\frac{1}{\sqrt{1-{\sin }^2\frac{{\theta }_m}{2}·{\text{sn}}^2(z)}}\frac{du}{dt}\\ \frac{du}{dt}=\sin \frac{{\theta }_m}{2}\frac{d}{dt}\text{sn}(z)=\sin \frac{{\theta }_m}{2}\text{cn}(z)\text{dn}(z)\frac{dz}{dt}=\omega \sin \frac{{\theta }_m}{2}\text{cn}(z)\text{dn}(z)\\ \frac{d\theta }{dt}=\sin \frac{{\theta }_m}{2}\frac{2\omega }{\sqrt{1-{\sin }^2\frac{{\theta }_m}{2}·{\text{sn}}^2\left(\omega \left(\pm t+t_0\right),\sin \frac{{\theta }_m}{2}\right)}}\text{cn}\left(\omega \left(\pm t+t_0\right),\sin \frac{{\theta }_m}{2}\right)\text{dn}\left(\omega \left(\pm t+t_0\right),\sin \frac{{\theta }_m}{2}\right)\end{array}}$

th_0=pi/2; %posición angular inicial
w=sqrt(9.8); %sqrt(g/l), l=1 m
t=linspace(0,4,100);
hold on
for w0=[-4,0,4] %velocidad angular inicial
    th_m=acos(cos(th_0)-w0^2/(2*w^2));
    gamma=asin(sin(th_0/2)/sin(th_m/2));
    t0=ellipticF(gamma,sin(th_m/2)^2)/w;
    signo=1;
    if w0<0
        signo=-1;
    end
    [sn,cn,dn]=ellipj(w*(signo*t+t0),sin(th_m/2)^2);
    v_ang=signo*2*w*sin(th_m/2)*cn.*dn./sqrt(1-(sin(th_m/2)*sn).^2); 
    plot(t,v_ang)
end
hold off
grid on
legend('-4','0','4', 'location','best')
xlabel('t')
ylabel('d\theta/dt')
title('Péndulo simple, oscilaciones')

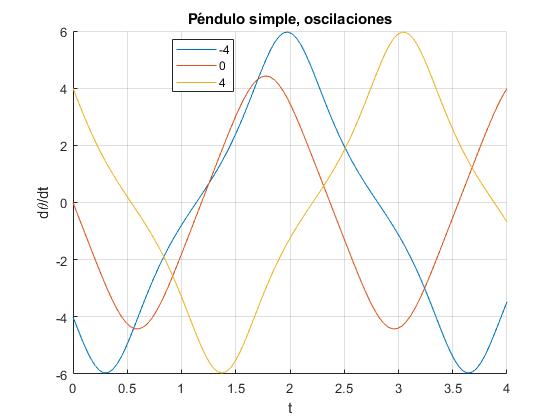
Comprobamos que la solución analítica que hemos obtenido, es similar a la solución aplicando procedimientos numéricos

th_0=pi/2; %posición angular inicial
w=sqrt(9.8); %sqrt(g/l), l=1 m
f=@(t,x) [x(2);-w^2*sin(x(1))]; 
hold on
for w0=[-4,0,4] %velocidad angular inicial  
   [t,x]=ode45(f,[0,4],[th_0, w0]);
   plot(t,x(:,2)) %velocidad angular
end
hold off
grid on
legend('-4','0','4', 'location', 'best')
xlabel('t')
ylabel('d\theta/dt')
title('Péndulo simple, oscilaciones')

Periodo

En el caso de un péndulo cuya posición inicial es θ₀ y su velocidad inicial es w₀, el máximo desplazamiento es

${\displaystyle \cos {\theta }_m=\cos {\theta }_0-\frac{w_0^2}{2{\omega }^2}}$

El periodo es cuatro veces el tiempo que tarda el péndulo en desplazarse desde θ=0, hasta θ_m

${\displaystyle \begin{array}{l}P=4{\displaystyle \underset{0}{\overset{{\theta }_{\max }}{\int }}\frac{d\theta }{\sqrt{w_0^2-2{\omega }^2\cos {\theta }_0+2{\omega }^2\cos \theta }}}\\ P=4\sqrt{\frac{2}{b}}F\left({\gamma }_m,\frac{1}{r}\right)=\frac{4}{\omega }F\left(\frac{\pi }{2},\sin \frac{{\theta }_m}{2}\right)=\frac{4}{\omega }K\left(\sin \frac{{\theta }_m}{2}\right)\end{array}}$

En un Movimiento Armónico Simple, x=Asin(ωt+φ), es una función periódica de periodo P, tal que cuando se incrementa el tiempo t en P, la fase (argumento del seno) se incrementa en 2π

ω(t+P)+φ=ωt+φ+2π, P=2π/ω

Del mismo modo sn(ω(t+t₀), sin(θ_m/2)) es una función periódica que cuando el tiempo se incrementa en P, el argumento de sn se incrementa en 4K(sin(θ_m/2))

${\displaystyle P=\frac{4}{\omega }K\left(\sin \frac{{\theta }_m}{2}\right)}$

Elaboramos un script para calcular los periodos para las velocidades angulares w₀=0, 4, cuando el péndulo parte de la posición inicial θ₀=π/2

th_0=pi/2; %posición angular inicial
w=sqrt(9.8); %sqrt(g/l), l=1 m
for w0=[0,4] %velocidad angular inicial
    th_m=acos(cos(th_0)-w0^2/(2*w^2));
    P=4*ellipke(sin(th_m/2)^2)/w; %periodo 
    disp(P)
end

    2.3690
    3.3455

Representamos las oscilaciones en el espacio de las fases, en el eje X, la posición angular θ, en el eje Y la velocidad angular dθ/dt durante un tiempo igual al periodo de oscilación P. Las trayectorias, para la velocidad angular inicial w₀=4 y w₀=-4 coinciden ya que tienen la misma energía, aunque el sentido del movimiento sea opuesto.

th_0=pi/2; %posición angular inicial
w=sqrt(9.8); %sqrt(g/l), l=1 m
t=linspace(0,4,100);
hold on
for w0=[-4,0,4] %velocidad angular inicial
    th_m=acos(cos(th_0)-w0^2/(2*w^2));
    gamma=asin(sin(th_0/2)/sin(th_m/2));
    t0=ellipticF(gamma,sin(th_m/2)^2)/w;
    signo=1;
    if w0<0
        signo=-1;
    end
    [sn,cn,dn]=ellipj(w*(signo*t+t0),sin(th_m/2)^2);
    th=2*asin(sn*sin(th_m/2));
    v_ang=signo*2*w*sin(th_m/2)*cn.*dn./sqrt(1-(sin(th_m/2)*sn).^2); 
    plot(th,v_ang)
end
hold off
grid on
legend('-4','0','4', 'location','best')
xlabel('\theta')
ylabel('d\theta/dt')
title('Péndulo simple, oscilaciones')

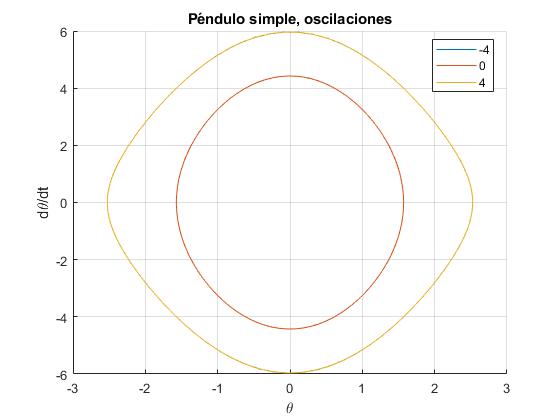
Rotaciones

Se producen cuando la velocidad angular inicial es mayor que la crítica, w₀>w_c. Cuando la energía del péndulo es mayor que la potencial del péndulo invertido, 2mgl

${\displaystyle \begin{array}{l}\frac{1}{2}m{l}^2{w}_0^2+mgl(1-\cos {\theta }_0)>2mgl\\ w_0^2-2{\omega }^2\cos {\theta }_0>2{\omega }^2\\ a>b\end{array}}$

La primera solución que aparece en la tabla de integrales corresponde a las rotaciones del péndulo, para el intervalo 0≤θ≤π

${\displaystyle \begin{array}{l}t={\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{d\theta }{\sqrt{w_0^2-2{\omega }^2\cos {\theta }_0+2{\omega }^2\cos \theta }}}-{\displaystyle \underset{0}{\overset{{\theta }_0}{\int }}\frac{d\theta }{\sqrt{w_0^2-2{\omega }^2\cos {\theta }_0+2{\omega }^2\cos \theta }}}\\ t=\frac{2}{\sqrt{a+b}}F\left(\frac{\theta }{2},r\right)-\frac{2}{\sqrt{a+b}}F\left(\frac{{\theta }_0}{2},r\right),r=\sqrt{\frac{2b}{a+b}}\\ t=\frac{2}{\sqrt{a+b}}F\left(\frac{\theta }{2},r\right)-t_0\\ \frac{\sqrt{a+b}}{2}(t+t_0)=F\left(\frac{\theta }{2},r\right)\end{array}}$

Posición angular

Despejamos la posición angular θ en función del tiempo t, utilizando la función elíptica sn de Jacobi

${\displaystyle \begin{array}{l}\sin \left(\frac{\theta }{2}\right)=\text{sn}\left(\frac{\sqrt{a+b}}{2}(t+t_0),r\right)\\ \theta =2\arcsin \left(\text{sn}\left(\frac{\sqrt{a+b}}{2}(t+t_0),r\right)\right),\frac{1}{r}=\sqrt{\frac{w_0^2}{4{\omega }^2}+{\sin }^2\left(\frac{{\theta }_0}{2}\right)}\end{array}}$

Periodo

El periodo es doble del tiempo que tarda en desplazarse de 0 a π

${\displaystyle \begin{array}{l}P=2{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{d\theta }{\sqrt{w_0^2-2{\omega }^2\cos {\theta }_0+2{\omega }^2\cos \theta }}}\\ P=\frac{4}{\sqrt{a+b}}F\left(\frac{\pi }{2},r\right)=\frac{4}{\sqrt{a+b}}K(r)\end{array}}$

Representamos la posición angular θ en función del tiempo t, para la posición angular inicial θ₀=π/2 y la velocidad angular inicial w₀=5 rad/s. Para esta posición angular inicial, la velocidad angular crítica es w_c=4.4272 rad/s. Por tanto, el péndulo describe una rotación

Dividimos el movimiento del péndulo en dos etapas:

• Desde θ₀ a π, o bien, entre los instantes t=0 y t₁=P/2-t₀

${\displaystyle \begin{array}{l}{t}_1={\displaystyle \underset{{\theta }_0}{\overset{\pi }{\int }}\frac{d\theta }{\sqrt{w_0^2-2{\omega }^2\cos {\theta }_0+2{\omega }^2\cos \theta }}}=\\ {\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{d\theta }{\sqrt{w_0^2-2{\omega }^2\cos {\theta }_0+2{\omega }^2\cos \theta }}}-{\displaystyle \underset{0}{\overset{{\theta }_0}{\int }}\frac{d\theta }{\sqrt{w_0^2-2{\omega }^2\cos {\theta }_0+2{\omega }^2\cos \theta }}}=\\ \frac{P}{2}-t_0\end{array}}$

La posición angular θ en función del tiempo t es

${\displaystyle \theta =2\arcsin \left(\text{sn}\left(\frac{\sqrt{a+b}}{2}(t+t_0),r\right)\right)}$

• Desde π a 2π+θ₀ o bien, entre los instantes P/2-t₀ a P

La posición angular θ en función del tiempo t es

${\displaystyle \theta =2\pi -2\arcsin \left(\text{sn}\left(\frac{\sqrt{a+b}}{2}(t+t_0),r\right)\right)}$

th_0=pi/2; %posición angular inicial
w=sqrt(9.8); %sqrt(g/l), l=1 m
w0=5; %velocidad angular inicial
b=2*w^2;
a=w0^2-2*w^2*cos(th_0);
r=sqrt(2*b/(a+b));
P=4*ellipke(r^2)/sqrt(a+b); %periodo
t0=2*ellipticF(th_0/2,r^2)/sqrt(a+b); 
t1=linspace(0,P/2-t0,100); 
sn=ellipj(sqrt(a+b)*(t1+t0)/2,r^2);  
th1=2*asin(sn);  %de th_0 a pi
t2=linspace(P/2-t0,P,100); 
sn=ellipj(sqrt(a+b)*(t2+t0)/2,r^2); 
th2=2*pi-2*asin(sn); %de pi a 2pi+th_0

hold on
plot([t1,t2],[th1,th2])
plot(P/2-t0, pi, 'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
line([P/2-t0, P/2-t0],[0,pi], 'lineStyle','--','color','k')
line([0, P/2-t0],[pi,pi], 'lineStyle','--','color','k')
hold off
grid on
xlabel('t')
ylabel('\theta')
title('Péndulo simple, rotaciones')

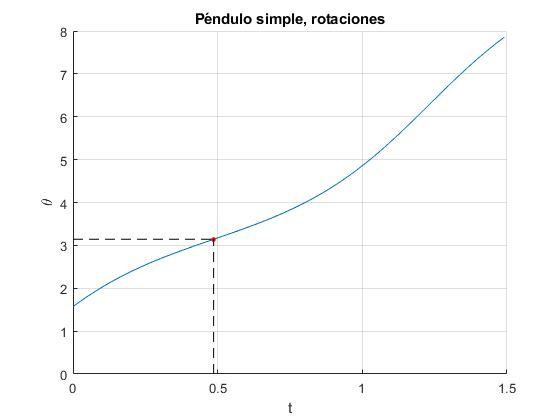
Comprobamos que la solución analítica que hemos obtenido, es similar a la solución aplicando procedimientos numéricos

th_0=pi/2; %posición angular inicial
w0=5; %velocidad angular inicial
w=sqrt(9.8); %sqrt(g/l), l=1 m
b=2*w^2;
a=w0^2-2*w^2*cos(th_0);
r=sqrt(2*b/(a+b));
P=4*ellipke(r^2)/sqrt(a+b); %periodo

f=@(t,x) [x(2);-w^2*sin(x(1))]; 
[t,x]=ode45(f,[0,P],[th_0, w0]);
plot(t,x(:,1)) %velocidad angular
grid on
xlabel('t')
ylabel('\theta')
title('Péndulo simple, rotaciones')

Cuando la velocidad angular inicial w₀ es cercana a la velocidad crítica w_c, en péndulo pasa mucho tiempo en las proximidades de θ=π (posición de equlibrio inestable). En el script cambiamos w₀=4.43 rad/s>w_c=4.4272

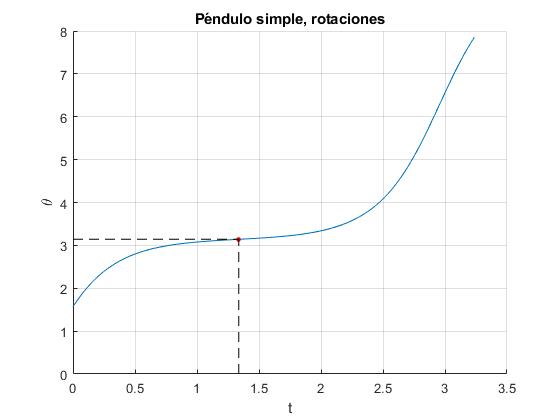
Se empiezan a apreciar diferencias entre la solución analítica y numérica

Velocidad angular

Dada la posición angular θ(t) respecto del tiempo, derivamos para calcular la velocidad angular, dθ/dt. El lector puede consultar la fórmula de la derivada de la función elíptica de Jacobi, sn(x)

${\displaystyle \begin{array}{l}\theta =2\arcsin (u),u=\text{sn}\left(\frac{\sqrt{a+b}}{2}(t+t_0),r\right)=\text{sn}(z)\\ \frac{d\theta }{dt}=2\frac{1}{\sqrt{1-u^2}}\frac{du}{dt}=2\frac{1}{\sqrt{1-{\text{sn}}^2(z)}}\frac{du}{dt}=\frac{2}{\text{cn}(z)}\frac{du}{dt}\\ \frac{du}{dt}=\frac{d}{dt}\text{sn}(z)=\text{cn}(z)\text{dn}(z)\frac{dz}{dt}=\frac{\sqrt{a+b}}{2}\text{cn}(z)\text{dn}(z)\\ \frac{d\theta }{dt}=\sqrt{a+b}·\text{dn}\left(\frac{\sqrt{a+b}}{2}(t+t_0),r\right)\end{array}}$

Representamos la velocidad angular (dθ/dt) para la posición angular inicial θ₀=π/2, y la velocidad angular inicial w₀=4.43 rad/s, próxima a la crítica.

th_0=pi/2; %posición angular inicial
w=sqrt(9.8); %sqrt(g/l), l=1 m
w0=4.43; %velocidad angular inicial
b=2*w^2;
a=w0^2-2*w^2*cos(th_0);
r=sqrt(2*b/(a+b));
P=4*ellipke(r^2)/sqrt(a+b); %periodo
t0=2*ellipticF(th_0/2,r^2)/sqrt(a+b);
t=linspace(0,P,200); 
[sn,cn,dn]=ellipj(sqrt(a+b)*(t+t0)/2,r^2);
v_ang=sqrt(a+b)*dn; %velocidad angular

plot(t, v_ang)
grid on
xlabel('t')
ylabel('d\theta/dt')
title('Péndulo simple, rotaciones')

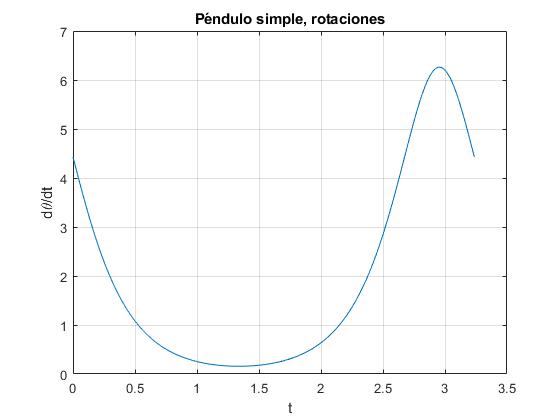
Comprobamos que la solución analítica que hemos obtenido, es similar a la solución aplicando procedimientos numéricos

th_0=pi/2; %posición angular inicial
w0=4.43; %velocidad angular inicial
w=sqrt(9.8); %sqrt(g/l), l=1 m
b=2*w^2;
a=w0^2-2*w^2*cos(th_0);
r=sqrt(2*b/(a+b));
P=4*ellipke(r^2)/sqrt(a+b); %periodo

f=@(t,x) [x(2);-w^2*sin(x(1))]; 
[t,x]=ode45(f,[0,P],[th_0, w0]);
plot(t,x(:,2)) %velocidad angular
grid on
xlabel('t')
ylabel('d\theta/dt')
title('Péndulo simple, rotaciones')

Referencias

F.M.S. Lima. Analytical study of the critical behavior of the nonlinear pendulum. Am. J. Phys. 78 (11), November 2010, pp. 1146-1151

I.S. Gradshteyn, I.M. Ryzhik. Table of Integrals, Series, and Products. Seventh Edition. Elsevier, 2007

J. P. Juchem Neto. Nonlinear Pendulum: A Simple Generalization. https://arxiv.org/abs/1007.4026. July 26, 2010