Movimiento de una partícula cargada en un campo eléctrico y en un campo magnético
Movimiento en un campo eléctrico
Una partícula cargada que está en una región donde hay un campo eléctrico, experimenta una fuerza igual al producto de su carga por la intensidad del campo eléctrico .
- Si la carga es positiva, experimenta una fuerza en el sentido del campo
- Si la carga es negativa, experimenta una fuerza en sentido contrario al campo
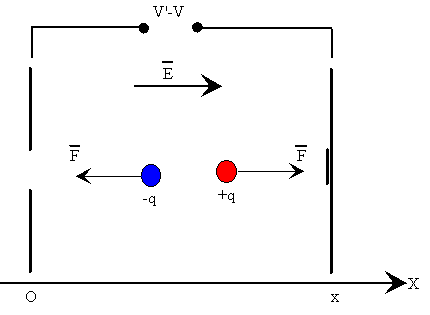
Si el campo es uniforme, la fuerza es constante y también lo es, la aceleración. Aplicando las ecuaciones del movimiento rectilíneo uniformemente acelerado, obtenemos la velocidad de la partícula en cualquier instante o después de haberse desplazado una determinada distancia
Aplicamos el principio de conservación de la energía, ya que el campo eléctrico es conservativo. La energía potencial q(V'-V) se transforma en energía cinética. Siendo V'-V la diferencia de potencial existente entre dos puntos distantes x. En un campo eléctrico uniforme V'-V=Ex.
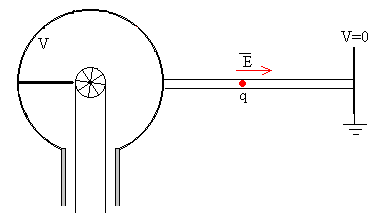
El generador de Van de Graaff se emplea para acelerar partículas. En el terminal esférico del generador se producen iones positivos que son acelerados a lo largo de un tubo en el que se ha hecho el vacío, por la diferencia de potencial existente entre la esfera cargada y tierra.
Movimiento en un campo magnético
 |
 |
Una partícula que se mueve en un campo magnético experimenta una fuerza . El resultado de un producto vectorial es un vector de
- módulo igual al producto de los módulos por el seno del ángulo comprendido qvB sinθ
- dirección perpendicular al plano formado por los vectores velocidad y campo .
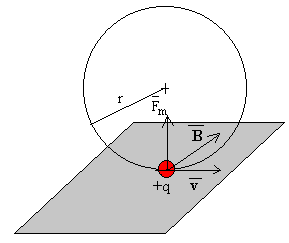
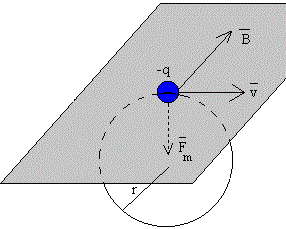
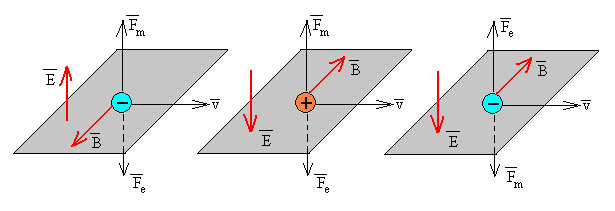
- y el sentido se obtiene por la denominada regla del sacacorchos. Si la carga es positiva el sentido es el del producto vectorial , como en la figura izquierda. Si la carga es negativa el sentido de la fuerza es contrario al del producto vectorial , figura de la derecha
Una partícula cargada describeuna trayectoria circular en un campo magnético uniforme. El radio, se obtiene a partir de la ecuación de la dinámica del movimiento circular uniforme: fuerza igual a masa por aceleración normal.
Hemos obtenido el radio r de la trayectoria circular, pero no conocemos la posición del centro dada la posición inicial y la velocidad inicial v de la partícula cargada. Al final de la página, haremos un estudio más completo
Estudiaremos en esta página y las que siguen, varias situaciones en las que una partícula cargada positiva o negativa se mueve en una región donde existe un campo eléctrico, un campo magnético, o un campo eléctrico y magnéticos cruzados (perpendiculares entre sí).
Movimiento en un campo eléctrico y magnéticos cruzados
En este apartado, vamos a practicar con las fuerzas que ejercen un campo magnético y un campo eléctrico sobre partículas cargadas en movimiento.
El campo eléctrico está creado por las dos placas de un condensador plano-paralelo que distan d y tienen una longitud L, su sentido es de la placa positiva (color rojo) a la negativa (color azul).
El campo magnético es perpendicular al plano de la página, es positivo cuando apunta hacia dentro (color azul claro) y es negativo cuando apunta hacia fuera (color rosa).
-
Desviación nula de la partícula
- El campo eléctrico ejerce una fuerza
- El campo magnético ejerce una fuerza
-
Movimiento bajo la acción del campo eléctrico
-
Movimiento bajo la acción de un campo magnético
Una carga eléctrica se mueve con velocidad v0 desconocida a lo largo del eje horizontal X. Buscaremos las intensidades y los sentidos de los campos eléctrico y magnético que hacen que la partícula se mueva a lo largo del eje X sin desviarse.
Las partículas no se desvían si ambas fuerzas son iguales y de sentido contrario.
Por tanto, no se desviarán aquellas partículas cuya velocidad sea igual cociente E/B.
En la figura, se muestran algunas configuraciones del campo eléctrico y magnético sobre cargas positivas o negativas que producen fuerzas en sentido contrario.
Cuando eliminamos el campo magnético, la partícula se mueve bajo la acción de la fuerza eléctrica en la región del condensador. Como la fuerza eléctrica constante tiene dirección del eje Y y la partícula se mueve inicialmente a lo largo del eje X, las ecuaciones del movimiento de la partícula serán las del tiro parabólico (movimiento bajo la aceleración constante de la gravedad)
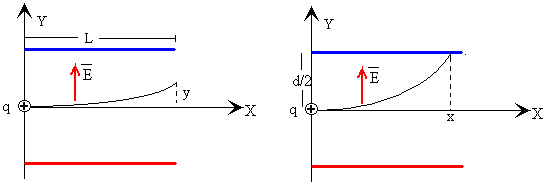
Si L es la longitud del condensador, la desviación vertical y de la partícula al salir de sus placas será
Puede ocurrir que la partícula choque con las placas del condensador. La posición x de impacto se calcula poniendo y=d/2, siendo d la distancia entre las placas del condensador.
En esta región, la partícula experimenta una fuerza debida al campo magnético, cuya dirección y sentido viene dada por el producto vectorial y cuyo módulo es fm=q·vB.
Aplicando la ecuación de la dinámica del movimiento circular uniforme, calculamos el radio de la circunferencia que describe.
La partícula cargada describe un arco de una circunferencia hasta que choca con alguna de las placas del condensador.
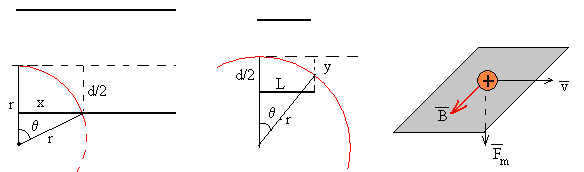
Si d es la separación entre las placas. El punto de impacto x, tal como se aprecia en la figura, se calcula del siguiente modo
Si el radio r es suficientemente grande, la partícula saldría entre las placas del condensador. Su desviación y se calcularía del siguiente modo
Ejemplo:
Datos de la partícula
- carga q=1.6·10-19 C
- masa m=1.67·10-27 kg
- campo eléctrico E=2000 N/C
- velocidad de la partícula 2·105 m/s
Observamos que para B=-100 gauss=-100·10-4 T, la partícula no se desvía. Su velocidad es
-
Suprimimos el campo magnético, la desviación que experimenta la partícula debido a la acción del campo eléctrico al final del condensador es
-
Suprimimos el campo eléctrico y restauramos el campo magnético B=-100 gauss
El radio de la órbita circular que describe la partícula es
La posición x de la partícula al chocar con la placa inferior es
20.87-5=20.87·cosθ, θ=40.5º
x=20.87·sinθ=13.56 cm
Actividades
Se introduce
-
La velocidad v0 de la partícula cargada en unidades ·105 m/s, en el control titulado Velocidad
-
La intensidad del campo eléctrico en N/C, en el control titulado C. eléctrico
-
La intensidad del campo magnético en gauss (10-4 T) en el control titulado magnético
-
La carga positiva o negativa del ión (una unidad de carga es 1.6·10-19 C) en el control titulado Carga
-
La masa de la partícula (una u.m.a. es 1.67·10-27 kg) en el control titulado Masa
Se pulsa el botón titulado Nuevo
Centro de la trayectoria circular
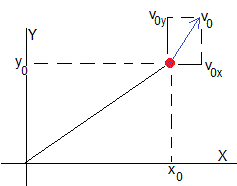
Hasta ahora, hemos considerado que el campo magnético es paralelo al eje Z, y la partícula cargada se mueve en el plano XY. La partícula describe una trayectoria circular de radio r=mv/qB.
Consideremos una partícula cargada de masa m y carga q que parte de , con velocidad , en un campo magnético uniforme paralelo al eje Z,
La ecuación del movimiento es
Donde la frecuencia angular, ω=qB/m
Si v0z=0, la trayectoria es un circunferencia. Si v0z≠0 la trayectoria es helicoidal
-
Componentes vx y vy de la velocidad en función del tiempo t
Coordenadas x e y de la partícula en función del tiempo t
La tercera ecuación diferencial es la más sencilla. Se trata de un movimiento uniforme a lo largo del eje Z
Derivamos la primera ecuación diferencial respecto del tiempo t
La solución vx es conocida
Los coeficientes c1 y c2 se calcularán a partir de las condiciones inciales. La solución vy es
Introduciendo vx y vy en la primera ecuación diferencial de vx
Las condiciones iniciales son
Conocidad la velocidad, la posición de la partícula cargada es
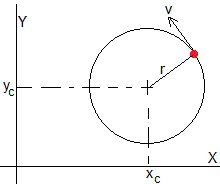
Las coordenadas (xc, yc) del centro de la trayectoria circular son
Deducción alternativa
Buscamos la solución del sistema de dos ecuaciones diferenciales empleando números complejos
Llamando
La ecuación característica es r2+iωr=0, cuyas raíces son: r1=0, y r2=iω
La solución de la ecuación diferencial es
Donde c1 y c2 son coeficientes complejos que se determinan a partir de las condiciones iniciales
El resultado es
Coincide con el que hemos calculado por otro procedimiento
Trayectoria helicoidal
En el plano XY la trayectoria es una circunferencia, cuyo centro es (xc, yc). El tiempo que tarda en dar una vuelta (periodo) es P=2π/ω, y en ese tiempo la partícula se desplaza a lo largo del eje Z, v0z·P
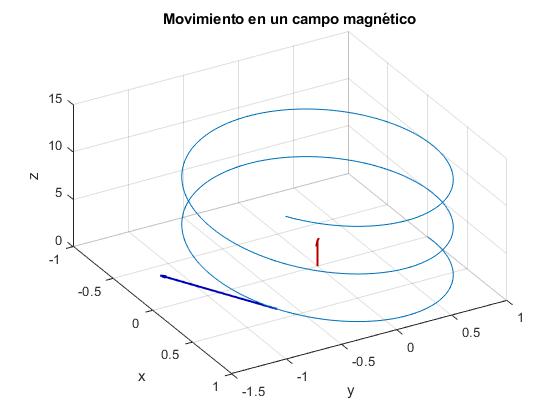
Representamos la trayectoria de una partícula cargada cuya velocidad v0y=0 y que parte de y0=v0x/ω, x0=0. El centro está situado en el origen
Representamos el vector velocidad (azul) en el instante t=5, tangente a la trayectoria, y el campo magnético paralelo al eje Z (rojo)
w=0.5; %frecuencia angular
vz=0.4; %eje Z
v0x=0.5; %velocidad inicial
r=v0x/w; %radio de la circunferencia
t=0:0.1:30;
x=r*sin(w*t); %trayectoria
y=r*cos(w*t);
z=vz*t;
hold on
plot3(x,y,z);
tp=5; %vector velocidad
h1=quiver3(r*sin(w*tp),r*cos(w*tp),vz*tp, v0x*cos(w*tp)/w,-v0x*sin(w*tp)/w,vz);
set(h1,'Color',[0,0,0.7],'LineWidth',1.5)
h1=quiver3(0,0,0,0,0,3); %campo magnético
set(h1,'Color',[0.7,0,0],'LineWidth',1.5)
hold off
view(60,46)
grid on
xlabel('x')
ylabel('y')
zlabel('z')
title('Movimiento en un campo magnético')
Problema
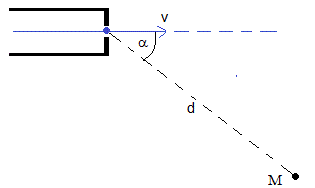
Un cañón emite electrones acelerados por una diferencia de potencial U, en el vacío en la dirección horizontal. El blanco M está a una distancia d, del cañón y en una dirección que forma un ángulo α con la horizontal, tal como se muestra en la figura.
- Calcular el campo magnético B, para que el haz de electrones impacte en el blanco M.
Datos: U=1000 V, q=1.60·10-19 C, m=9.11·10-31 kg, α=60°, d=5.0 cm.
Campo perpendicular al plano
En primer lugar, consideramos que el campo magnético es perpendicular a plano formado por el haz y el blanco M (el plano del dibujo)
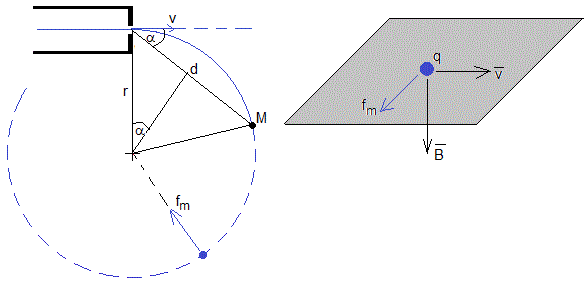
Los electrones describirán una trayectoria circular de radio r, ya que la fuerza que ejerce el campo magnético es perpendicular a la velocidad y al campo,
La ecuación de la dinámica del movimiento circular uniforme se escribe
Como vemos en la figura, d=2rsinα
Por otra parte, el cañón acelera los electrones, de modo que la energía potencial qU se convierte en energía cinética
El módulo del campo magnético B vale
Con los datos del problema, B=0.0037 T
Campo paralelo al plano
Consideremos que el campo es paralelo a la dirección del blanco M, vamos a comprobar que el haz de electrones impacta en el blanco M siguiendo una trayectoria helicoidal
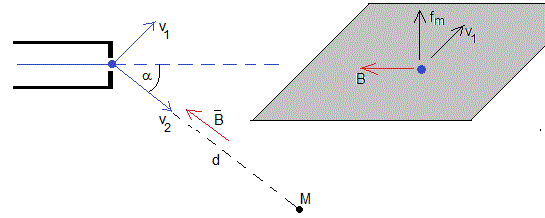
Descomponemos la velocidad horizontal v del haz de electrones en dos componentes v1=v·sinα y v2=v·cosα, tal como se muestra en la figura. El haz de electrones describirá una trayectoria circular de radio r en un plano perpendicular a la direccción del blanco
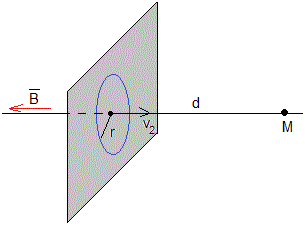
El periodo P, es el tiempo que tarda en dar una vuelta completa
La componente v2=v·cosα hace que la partícula se desplace a lo largo de la dirección del blanco M, tardando un tiempo t=d/v2
Cuando t=n·P el haz impactará en el blanco M
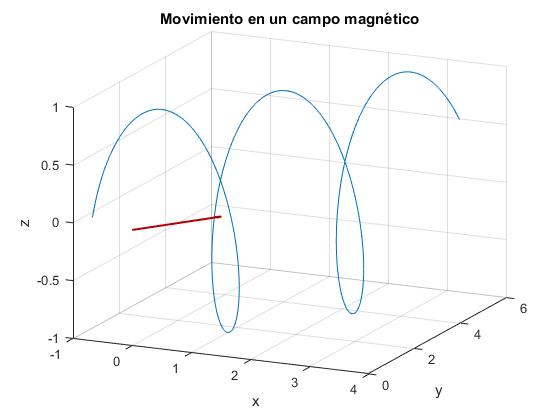
Con los datos del problema, B=n·0.0067 T. Dando valores enteros a n=1,2,3... obtenemos los posibles valores de B que hacen que el haz de electrones impacte en el blanco M siguiendo una trayectoria helicoidal, como se ve en la figura. El segmento de color rojo indica la dirección del campo magnético
r=1;
w=0.5;
vz=0.2;
t=0:0.01:30;
zp=r*sin(w*t);
y=r*cos(w*t);
x=vz*t;
xp=x*cos(pi/3)-y*sin(pi/3);
yp=x*sin(pi/3)+y*cos(pi/3);
hold on
plot3(xp,yp,zp);
h1=quiver3(0,0,0, 2*cos(pi/3),2*sin(pi/3),0);
set(h1,'Color',[0.7,0,0],'LineWidth',1.5)
hold off
%axis equal
view(25,20)
grid on
xlabel('x')
ylabel('y')
zlabel('z')
title('Movimiento en un campo magnético')
Referencias
O. L. de Lange, J. Pierrus. Solved Problems in Classical Mechanics. Analytical and numerical solutions with comments. Question 7.17, pp. 187-189
Problema propuesto en la X Olimpiada Internacional de Física. Hradec Králové, Checoslovaquia, 1977
Orion Ciftja, Cleo L. Bentley Jr. Circular Motion of a Charged Particle in a Uniform Constant Magnetic Field Revisited. The Physics Teacher, Vol.63, April 2025. pp. 269-273

