El acelerador de inducción magnética o betatrón, pertenece al grupo de máquinas ideadas para acelerar partículas cargadas hasta elevadas energías. Fue inventado en 1941 por Donald W. Kerst. El betatrón construido en 1945 aceleraba electrones hasta una energía de 10⁸ eV.

El acelerador consistía en un tubo toroidal en el que se había hecho el vacío, y se situaba entre las piezas polares de un electroimán. Los electrones, acelerados mediante una diferencia de potencial de unos 50000 voltios por un cañón electrónico, entraban tangencialmente dentro del tubo, donde el campo magnético les hacía dar vueltas en una órbita circular de 5 m de longitud.

Los betatrones se usan para estudiar ciertos tipos de reacciones nucleares y como fuentes de radiación para el tratamiento del cáncer.

La fuerza que ejerce el campo magnético, como hemos visto ya en el espectrómetro de masas y en el ciclotrón obliga a las partículas a describir una órbita circular. El problema que surge en esta situación, es que a medida que las partículas son aceleradas, se necesita un campo magnético cada vez mayor para que las partículas describan una órbita circular de un determinado radio.

Ley de Faraday-Henry

En primer lugar, determinaremos el campo eléctrico en cada punto del espacio, producido por un campo magnético que tiene simetría axial (su módulo depende solamente de la distancia r al eje Z), pero a su vez, cambia con el tiempo.

El camino cerrado elegido es una circunferencia de radio r, centrada en el eje Z. Como el flujo varía con el tiempo, se induce una fem dada por la ley de Faraday

${\displaystyle V_{\epsilon }=-\frac{d\Phi }{dt},V_{\epsilon }={{{\displaystyle \oint }}^{\text{}}}^{\text{}}\overrightarrow{E}·\overrightarrow{dl},\Phi =\underset{S}{{{\displaystyle \int }}^{\text{}}}\overrightarrow{B}·\overrightarrow{dS}}$

Debido a la simetría axial, el campo eléctrico generado $\overrightarrow{E}$ solamente depende de r, es constante y tangente en todos los puntos de la circunferencia de radio r, de modo que V_ε=E·2π r

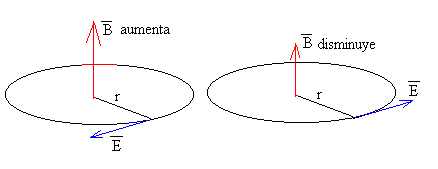
El flujo del campo magnético es Φ =<B>π r². Donde <B> es el campo medio existente en la región que cubre el área S=π r². Despejando el módulo del campo eléctrico

${\displaystyle E=-\frac{1}{2}r\frac{d<B>}{dt}}$

Movimiento de las partículas cargadas

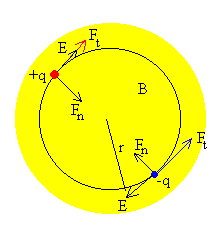
Ya que la partícula describe una trayectoria circular con velocidad variable con el tiempo, hemos de estudiar el movimiento de la partícula en la dirección tangencial y en la dirección normal.

• Movimiento en la dirección tangencial

La partícula cargada experimenta una fuerza F=qE, tangente a la circunferencia de radio r. Si la carga es positiva la fuerza es en el sentido del campo, y si la carga es negativa es en sentido contrario al campo.

La ecuación del movimiento de la partícula (masa por aceleración tangencial igual a la componente tangencial de la fuerza) será

${\displaystyle m\frac{dv}{dt}=-\frac{q}{2}r\frac{d<B>}{dt}}$

• Movimiento en la dirección radial



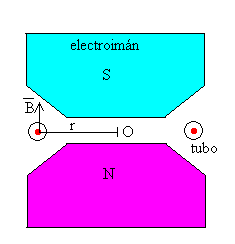
El campo magnético ejerce una fuerza centrípeta ($\overrightarrow{v}$ y $\overrightarrow{B}$ son mutuamente perpendiculares) F_n=qvB. La ecuación del movimiento (masa por aceleración normal igual a la componente normal de la fuerza que actúa sobre la partícula) es

${\displaystyle m\frac{v^2}{r}=qvB}$

Para que se cumplan simultáneamente las dos condiciones, el campo magnético a la distancia r del eje Z, tiene que ser igual a la mitad del campo magnético medio <B> en la región que cubre el área S=π r².

${\displaystyle B(r)=\frac{1}{2}<B>}$

Energía de las partículas cargadas

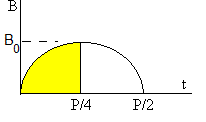
En general, el campo magnético B es oscilatorio, con frecuencia angular ω , pero las partículas solamente se aceleran cuando el campo magnético está aumentando.

Las partículas se inyectan cuando el campo magnético es cero, por tanto, las partículas se aceleran solamente durante un cuarto de periodo, de 0 a P/4. Al cabo de este tiempo, se les proporciona un impulso adicional que las dirige hacia el blanco.

En el instante t=P/4, cuando B adquiere su valor máximo B₀, la velocidad de las partículas es

m·v_m=qB₀·r

y la energía cinética máxima es

${\displaystyle E_{km}=\frac{q^2{r}^2{B}_0^2}{2m}}$

Si B=B₀·sin(ω t) la aceleración tangencial dada por

${\displaystyle a_t=\frac{qr}{m}{B}_0\omega \cos (\omega t)}$

Integrando obtenemos la velocidad de la partícula en cada instante, (suponemos que la partícula parte del reposo en el instante inicial t=0)

${\displaystyle v={\displaystyle \underset{0}{\overset{t}{\int }}{a}_{t}dt}=\frac{qr}{m}{B}_0\sin (\omega t)}$

Como vemos para ωt=π/2, o cuando t=P/4 se obtiene la máxima velocidad v_máx de las partículas aceleradas. La velocidad máxima es independiente del valor del periodo P. Dependiendo del valor de P, las partículas tardarán más o menos tiempo en alcanzar la velocidad máxima.

Actividades

El programa interactivo nos muestra los principios físicos en los que se basa el funcionamiento de un betatrón. Supondremos que, el campo magnético tiene simetría axial, y que la variación del campo magnético con la distancia radial r es tal que se cumple la condición para que las partículas cargadas describan una órbita circular de radio r.

Supondremos también, que el campo magnético apunta perpendicularmente hacia el plano de la pantalla y hacia dentro. Su módulo varía con el tiempo, de modo que su periodo es 4 unidades de tiempo (el periodo como hemos visto no influye para nada en el valor de la velocidad máxima). Las partículas cargadas son aceleradas durante una unidad de tiempo.

Como vemos el campo $\overrightarrow{E}$, es tangente a la circunferencia de radio r, y tiene el mismo valor en todos sus puntos. El radio r ha sido fijado en el programa y vale 0.5 m

Comprobamos, aplicando la ley de Lenz, el sentido del campo $\overrightarrow{E}$, cuando el campo magnético $\overrightarrow{B}$ aumente y cuando disminuya.

El sentido de la fuerza sobre la partícula cargada depende de su signo. Las partículas cargadas con carga positiva se aceleran en el sentido del campo, y las negativas en sentido contrario al campo.

Se observa que la energía máxima se obtiene cuando el campo magnético se hace máximo es decir, en el instante t=P/4=1 unidad de tiempo. A partir de este momento, el campo eléctrico cambia de signo y la partícula se frena hasta que se para. En la situación real cuando la partículas adquieren la máxima energía, reciben un impulso adicional que las hace salir de su órbita circular para dirigirse hacia el blanco.

En el gráfico de la parte superior derecha, se muestra la representación de B en función del tiempo, durante un semiperiodo.

En el gráfico de la parte inferior derecha, se muestra como la partícula va cambiando su energía cinética.

Se introduce:

• La carga q de las partículas, en unidades de la carga del electrón, 1.6·10^-19 C. El valor de la carga puede ser un número positivo o negativo.
• La masa m de la partícula en u.m.a. ó 1.67·10^-27 kg
• El campo magnético B en gauss (10^-4 T)
• El radio r de la circunferencia se ha fijado en 0.5 m en el programa interactivo

Se pulsa el botón titulado Nuevo.

Ejemplo

Sea q=+2e, m=4 uma y B=5 gauss, r=0.5 m

• la carga del electrón e=1.6·10^-19 C.
• una unidad de masa atómica, u.m.a. vale 1.67·10^-27 kg
• un gauss=10^-4 T

${\displaystyle E_{km}=\frac{{\left(2·1.6·{10}^{-19}\right)}^2{\left(0.5\right)}^2{\left(5·{10}^{-4}\right)}^2}{2·4·1.67·{10}^{-27}}=4.79·{10}^{-19}\text{J}=2.99\text{eV}}$

Movimiento de una partícula cargada en un campo magnético variable con el tiempo

Consideremos una región cilíndrica de radio r₀, donde hay un campo magnético uniforme paralelo al eje del cilindro y que cambia con el tiempo.

${\displaystyle \overrightarrow{B}(r,t)=\{\begin{array}{l}\mathrm{0,}r>r_0\\ B(t)\widehat{k},r<r_0\end{array}}$

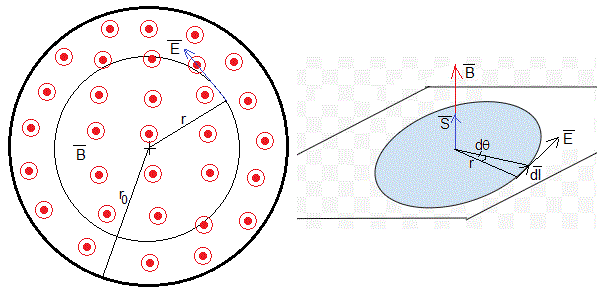
Se induce un campo eléctrico $\overrightarrow{E}(r,t)=E\widehat{\theta }$, tangente a la circunferencia de radio r, de acuerdo con la ley de Faraday

${\displaystyle \begin{array}{l}{\displaystyle \oint \overrightarrow{E}·\overrightarrow{dl}}=-\frac{d}{dt}{\displaystyle \underset{S}{\int }\overrightarrow{B}·\overrightarrow{dS}}\\ {\displaystyle \oint E(r·d\theta )·\cos 0}=-\frac{d}{dt}{\displaystyle \underset{S}{\int }B·dS}\\ 2\pi rE=-\frac{dB}{dt}{\displaystyle \underset{S}{\int }dS}\\ {\displaystyle \underset{S}{\int }dS}=\{\begin{array}{l}\pi r^2,r<r_0\\ \pi r_0^2,r>r_0\end{array}\end{array}}$

Despejando el módulo del campo eléctrico E

${\displaystyle E(r,t)=\{\begin{array}{l}-\frac{r}{2}\frac{dB}{dt},r<r_0\\ -\frac{r_0^2}{2r}\frac{dB}{dt},r>r_0\end{array}}$

Un campo magnético que cambia con el tiempo produce un campo eléctrico. Si la circunferencia de radio r coincide con un conductor se induce una corriente, con densidad $\overrightarrow{J}=\sigma \overrightarrow{E}$ , donde σ es la conductividad del metal. La dirección de la corriente coincide con la dirección del vector campo eléctrico $\overrightarrow{E}(r,t)$ y está de acuerdo con la ley de Lenz.

En la figura, se ha señalado la dirección del campo eléctrico cuando el campo magnético B(t) disminuye con el tiempo, dB/dt<0. Si el campo magnético aumentara con el tiempo, dB/dt>0, el campo eléctrico tendría sentido contrario

Ecuaciones del movimiento

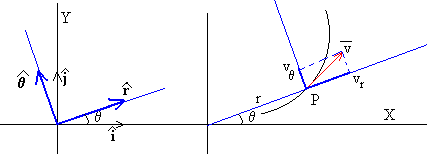
Las expresiones de la velocidad y aceleración en coordenadas polares son

${\displaystyle \begin{array}{l}\overrightarrow{v}=\frac{dr}{dt}\widehat{r}+r\frac{d\theta }{dt}\widehat{\theta }\\ \overrightarrow{a}=\left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)\widehat{r}+\left(r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}\right)\widehat{\theta }\end{array}}$

La fuerza que ejerce el campo eléctrico inducido y el campo magnético sobre la partícula cargada es

${\displaystyle \overrightarrow{F}=\overrightarrow{qE}+q\overrightarrow{v}\times \overrightarrow{B}=qE\widehat{\theta }+q\left(\frac{dr}{dt}\widehat{r}+r\frac{d\theta }{dt}\widehat{\theta }\right)\times B\widehat{k}=qr\frac{d\theta }{dt}B\widehat{r}+q\left(E-\frac{dr}{dt}B\right)\widehat{\theta }}$

Las ecuaciones del movimiento son

${\displaystyle \{\begin{array}{l}m\left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)=qBr\frac{d\theta }{dt}\\ m\left(r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}\right)=q\left(E-\frac{dr}{dt}B\right)\end{array}}$

Ejemplo

Supondremos que el campo magnético uniforme varía con el tiempo de la forma

${\displaystyle B(t)=B_0\left(1-e^{-t/t_0}\right)}$

fplot(@(t) 1-exp(-t), [0,10])
grid on
ylim([0,1.1])
xlabel('t')
ylabel('f(t)')
title('Campo magnético')

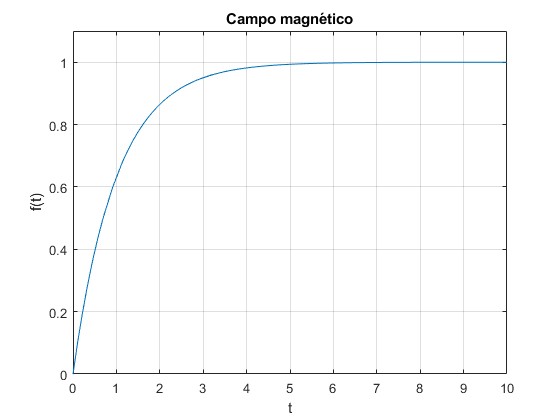
El campo magnético B crece y al cabo de un cierto tiempo, se hace casi constante

Expresamos las ecuaciones del movimiento en términos de las variables adimensionales

${\displaystyle R=\frac{r}{r_0},\tau =\frac{q{B}_0}{m}t}$

El campo magnético B se expresa

${\displaystyle B=B_0\left(1-e^{-\tau /{\tau }_0}\right)}$

El campo eléctrico E se expresa

${\displaystyle E(r,t)=\{\begin{array}{l}-\frac{r}{2}\frac{dB}{dt}=-\frac{r_{0}R}{2}\frac{q{B}_0}{m}\frac{dB}{d\tau }=-\frac{1}{2}\frac{r_{0}q{B}_0^2}{m}\frac{R{e}^{-\tau /{\tau }_0}}{{\tau }_0},R<1\\ -\frac{r_0^2}{2r}\frac{dB}{dt}=-\frac{r_0^2}{2r_{0}R}\frac{q{B}_0}{m}\frac{dB}{d\tau }=-\frac{1}{2}\frac{r_{0}q{B}_0^2}{m}\frac{e^{-\tau /{\tau }_0}}{{\tau }_{0}R},R\ge 1\end{array}}$

Resolvemos el sistema de dos ecuaciones diferenciales asignando al parámero τ₀=50, con las siguientes condiciones iniciales, en el instante τ=0, R=0, θ=0, dR/dt=0, dθ/dt=0

function betatron
    t0=50;
    [~,x]=ode45(@eDiferencial,[0,150],[0.4,0,0,0]);
    xx=x(:,1).*cos(x(:,3));
    yy=x(:,1).*sin(x(:,3));
    plot(xx,yy)
    axis equal
    grid on
    xlabel('x/r_0')
    ylabel('y/r_0');
    title('Trayectoria')

   function dr=eDiferencial(t,x)
        dr=zeros(4,1);
        dr(1)=x(2);
        dr(2)=x(1)*x(4)^2;
        if x(1)<1
            dr(2)=dr(2)+x(1)*x(4)*(1-exp(-t/t0));
        end
        dr(3)=x(4);
        dr(4)=-2*x(2)*x(4)/x(1);
        if x(1)<1
            dr(4)=dr(4)-exp(-t/t0)/(2*t0)-x(2)*(1-exp(-t/t0))/x(1);
        else
             dr(4)=dr(4)-exp(-t/t0)/(2*t0*x(1)^2);
        end   
   end
end

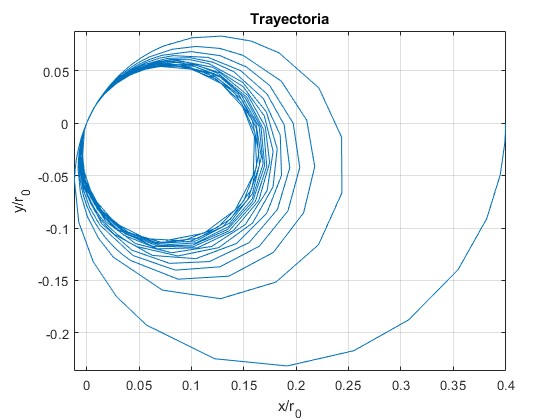
Después de un tiempo grande, la partícula cargada describe una trayectoria circular

La energía cinética de la partícula cargada cambia debido al campo eléctrico inducido, pero no la modifica la fuerza magnética ya que es perpendicular al desplazamiento y por tanto, no realiza trabajo alguno.

Las trayectorias finales circulares no aparecen cualquiera que sean las condición iniciales. Por ejemplo, para R=9/10 si se cumple que la velocidad incial tangencial dθ/dτ es mayor o menor que cierto valor crítico próximo a ±0.064. Por ejemplo

...
        [~,x]=ode45(@eDiferencial,[0,600],[9/10,0,pi/6,0.064]);
...

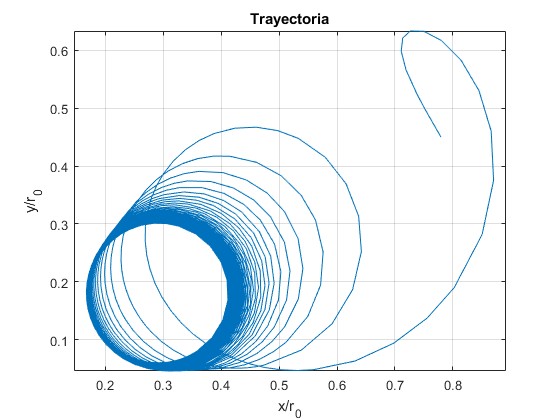
Si incrementamos dθ/dτ a 0.065 ya no aparece la trayectoria final circular. Se puede experimentar también con la velocidad inicial radial dR/dt.

Referencias

J. Pierrus. Solved Problems in Classical Electromagnetism. Analytical and numerical solutions with comments. Oxford University Press (2018). Questions 5.12, 5.13, pp. 268-271.