Difracción Fraunhofer producida por una abertura circular

En la figura, se muestra el obstáculo, una abertura circular de radio a y un punto P situado en una pantalla a una distancia R del obstáculo. La recta que une el centro del círculo y el punto, forma un ángulo θ con el eje Z.

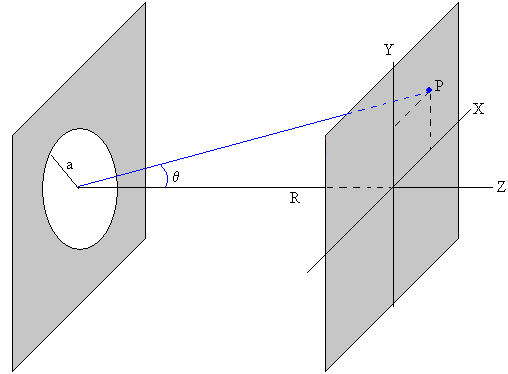
La expresión de la intensidad I(x, y) registrada en el punto P debido a la difracción por el obstáculo de ondas planas de longitud de onda λ, es

$I (x, y) = I (0) {(\frac{2 J_{1} (α)}{α})}^{2} α = \frac{2 π a}{λ} \sin θ$

Donde I(0) es la intensidad registrada en el origen de la pantalla

J_n(α) es la función de Bessel de orden n.

Máximos y mínimos

Los máximos de intensidad se producen cuando

$\begin{array}{l} \frac{d}{d α} (\frac{J_{1} (α)}{α}) = 0 \\ \frac{1}{α} \frac{d}{d α} J_{1} (α) - \frac{1}{α^{2}} J_{1} (α) = 0 \\ α \frac{d}{d α} J_{1} (α) - J_{1} (α) = 0 \end{array}$

Las funciones de Bessel tiene la siguiente relación de recurrencia

$x \frac{d}{d x} J_{n} (x) = n J_{n} (x) - x J_{n + 1} (x)$

Aplicando esta propiedad a la función J₁(α)

$α \frac{d}{d α} J_{1} (α) = J_{1} (α) - α J_{2} (α)$

Se concluye que los máximos secundarios de intensidad son los ceros de la función de Bessel J₂(α) que se calculan por procedimientos numéricos.

J₂(α)=0

Los mínimos de intensidad son los ceros de la función de Bessel J₁(α) que se calculan por procedimientos numéricos.

J₁(α)=0

Ahora bien, J₁(α) presenta un cero para α=0 y este corresponde a un máximo de intensidad, ya que

$\lim_{α \to 0} (\frac{2 J_{1} (α)}{α}) = 1$

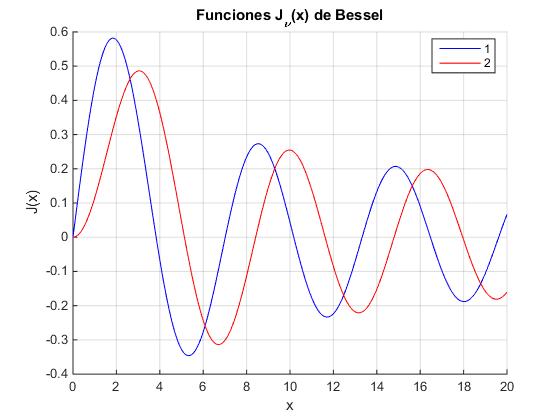
Representamos gráficamente las funciones J₁(x) y J₂(x)

color=['b','r'];
x=0:0.05:20;
hold on
for n=1:2
    y=besselj(n,x);
    plot(x,y,color(n),'displayName',num2str(n));
end
legend('-DynamicLegend','location','Best')
xlabel('x')
ylabel('J(x)')
title('Funciones J_\nu(x) de Bessel')
grid on
hold off

Actividades

Se pulsa el botón titulado Nuevo

Raíces de las funciones de Bessel J₁(x) y J₂(x)

Vamos a crear un procedimiento raices que nos permita buscar los intervalos en los que la función f(x) cambia de signo para calcular posteriormente la raíz buscada en cada uno de ellos, mediante la función fzero de MATLAB.

function r = raices(f, x)
    y=f(x);
    indices=find(y(1:end-1).*y(2:end)<0);
    r=zeros(1,length(indices));
    for k=1:length(indices)
        r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
    end
end

Pasamos a la función raices la función J₁(x) y el intervalo en el cual queremos calcular las raíces

x=linspace(0.1,30,50);
f=@(x) besselj(1,x);
k=raices(f,x); 
disp('mínimos: difracción por abertura circular')
disp(k')

En la ventana de comandos vemos los valores de las raíces la función J₁(x) en el intervalo de a=0.1 a b=30.

mínimos: difracción por abertura circular
    3.8317
    7.0156
   10.1735
   13.3237
   16.4706
   19.6159
   22.7601
   25.9037
   29.0468

Cambiamos la función J₁(x) por la función J₂(x), para determinar la posición de los máximos secundarios.

x=linspace(0.1,30,50);
f=@(x) besselj(2,x);
k=raices(f,x); 
disp('máximos secundarios de difracción por abertura circular')
disp(k')

En la ventana de comandos vemos los valores de las raíces la función J₂(x) en el intervalo de a=0.1 a b=30.

máximos secundarios de difracción por abertura circular
    5.1356
    8.4172
   11.6198
   14.7960
   17.9598
   21.1170
   24.2701
   27.4206

Medida del radio de la abertura circular

Cuando iluminamos una abertura circular, determinamos su radio contando el número de franjas que produce en una pantalla la luz difractada en un determinado intervalo angular.

Iluminamos una abertura circular de radio a del orden de μm, 10^-6 m con luz procedente de un láser He-Ne de longitud de onda λ=632.8·10^-9 m. Observamos la intensidad de la luz difractada en un intervalo angular entre 30 y 60º.

En la parte superior del programa interactivo (más abajo), se proporciona el gráfico de la intensidad

$\begin{array}{l} I (θ) = I_{0} {(\frac{J_{1} (α)}{α})}^{2} α = \frac{2 π a}{λ} \sin θ \\ α = \frac{2 π a \cdot 10^{- 6}}{632.8 \cdot 10^{- 9}} \sin θ = 9.929 \cdot a \cdot \sin θ \end{array}$

La intensidad correspondiente al máximo inmediatamente anterior a θ=30º se toma como unidad.

Contamos los máximos y mínimos de intensidad en el intervalo angular 30º-60º

En la parte central, se representa la intensidad en escala de grises. Contamos en número de franjas de difracción de color claro o de color oscuro en dicho intervalo angular, que será igual al número de máximos o mínimos, respectivamente.
En la parte inferior, se representa el radio de la abertura circular en función del número de franjas. Comprobamos la relación aproximadamente lineal entre estas dos magnitudes.

Se pulsa el botón titulado Nuevo

Se introduce

El radio a de la abertura circular (en μm) en el control titulado Radio.

Se pulsa el botón titulado Mide

Se cambia el valor del radio de la abertura circular

Se pulsa el botón titulado Mide

Y así, sucesivamente

Radio:

Referencias

Hecht E., Zajac A.Óptica. Addison-Wesley Iberoamericana (1977), págs. 369-379