Se emite luz de longitud de onda λ desde la fuente puntual S, que es difractada por la abertura rectangular de dimensiones 2a×2b, situada a una distancia ρ₀. La luz difractada se observa en una pantalla situada a una distancia r₀

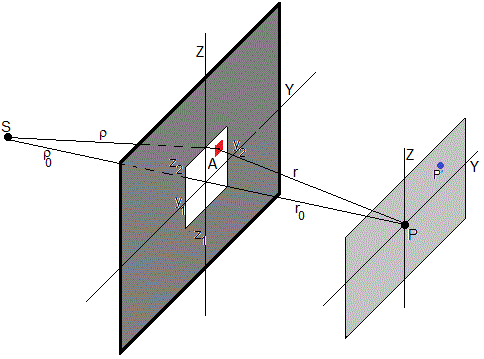
La onda esférica incidente emitida por la fuente S es

${\displaystyle E\left(\rho ,t\right)=\frac{E_0}{\rho }\exp \left(i\left(k\rho -\omega t\right)\right)}$

Se aplica el principio de Huygens-Fresnel para calcular el movimiento ondulatorio en un punto dado (Y,Z) de la pantalla, teniendo en cuenta la amplitud y fase, de las ondas elementales emitidas por los elementos de área (pequeño rectángulo de color rojo) dS=dx·dy de la abertura rectangular.

${\displaystyle E_P=\frac{-i{E}_0{e}^{-i\omega t}}{\lambda }{\displaystyle \underset{S}{\iint }k(\theta )\frac{e^{ik(\rho +r)}}{\rho r}}dS}$

Situamos el origen en el centro de la abertura rectangular. La fuente de ondas S dista ρ₀ del origen de la abertura y el punto de observación P dista r₀, que son grandes en comparación con el tamaño de la abertura

Teniendo en cuenta la aproximación

${\displaystyle \begin{array}{l}\frac{1}{\rho r}\approx \frac{1}{{\rho }_0{r}_0}\\ k(\theta )\approx 1\end{array}}$

La integral se convierte en

${\displaystyle E_P=\frac{-i{E}_0{e}^{-i\omega t}}{\lambda {\rho }_0{r}_0}{\displaystyle \underset{y_1}{\overset{y_2}{\int }}{\displaystyle \underset{z_1}{\overset{z_2}{\int }}{e}^{ik(\rho +r)}dy·dz}}}$

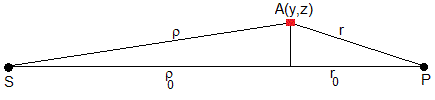
Aproximamos el exponente ρ+r

${\displaystyle \begin{array}{l}{\rho }^2={\rho }_0^2+y^2+z^2\\ \frac{\rho }{{\rho }_0}=\sqrt{1+\frac{y^2+z^2}{{\rho }_0^2}}\approx 1+\frac{1}{2}\frac{y^2+z^2}{{\rho }_0^2}\\ r^2=r_0^2+y^2+z^2\\ \frac{r}{r_0}=\sqrt{1+\frac{y^2+z^2}{r_0^2}}\approx 1+\frac{1}{2}\frac{y^2+z^2}{r_0^2}\end{array}}$

Hemos utilizado la aproximación, $\sqrt{1+x}\approx 1+\frac{x}{2}$

>> syms x;
>> taylor(sqrt(1+x),x)
ans =(7*x^5)/256 - (5*x^4)/128 + x^3/16 - x^2/8 + x/2 + 1

${\displaystyle \begin{array}{l}\rho +r\approx {\rho }_0\left(1+\frac{1}{2}\frac{y^2+z^2}{{\rho }_0^2}\right)+r_0\left(1+\frac{1}{2}\frac{y^2+z^2}{r_0^2}\right)\approx {\rho }_0+r_0+\frac{1}{2}\frac{y^2+z^2}{{\rho }_0}+\frac{1}{2}\frac{y^2+z^2}{r_0}=\\ {\rho }_0+r_0+\left(y^2+z^2\right)\frac{{\rho }_0+r_0}{2{\rho }_0{r}_0}\end{array}}$

La integral doble se convierte en producto de dos integrales

${\displaystyle \begin{array}{l}{E}_P=\frac{-i{E}_0\exp \left(i\left(k\left(r_0+{\rho }_0\right)-\omega t\right)\right)}{\lambda {\rho }_0{r}_0}{\displaystyle \underset{y_1}{\overset{y_2}{\int }}{\displaystyle \underset{z_1}{\overset{z_2}{\int }}\exp \left(ik\left(y^2+z^2\right)\frac{{\rho }_0+r_0}{2{\rho }_0{r}_0}\right)dy·dz}}=\\ \frac{-i{E}_0\exp \left(i\left(k\left(r_0+{\rho }_0\right)-\omega t\right)\right)}{\lambda {\rho }_0{r}_0}{\displaystyle \underset{y_1}{\overset{y_2}{\int }}\exp \left(ik{y}^2\frac{{\rho }_0+r_0}{2{\rho }_0{r}_0}\right)dy·{\displaystyle \underset{z_1}{\overset{z_2}{\int }}\exp \left(ik{z}^2\frac{{\rho }_0+r_0}{2{\rho }_0{r}_0}\right)dz}}\end{array}}$

Efectuamos el cambio de variable

${\displaystyle \begin{array}{l}\frac{\pi }{2}{u}^2=k{y}^2\frac{{\rho }_0+r_0}{2{\rho }_0{r}_0},\frac{\pi }{2}{v}^2=k{z}^2\frac{{\rho }_0+r_0}{2{\rho }_0{r}_0}\\ \pi u·du=ky\frac{{\rho }_0+r_0}{{\rho }_0{r}_0}dy\\ \pi \sqrt{\frac{k}{\pi }\frac{{\rho }_0+r_0}{{\rho }_0{r}_0}}·du=k\frac{{\rho }_0+r_0}{{\rho }_0{r}_0}dy\\ du=\sqrt{\frac{k}{\pi }\frac{{\rho }_0+r_0}{{\rho }_0{r}_0}}dy,dv=\sqrt{\frac{k}{\pi }\frac{{\rho }_0+r_0}{{\rho }_0{r}_0}}dz\end{array}}$

La onda en el punto P, E_P se escribe

${\displaystyle \begin{array}{l}{E}_P=\frac{-i{E}_0\exp \left(i\left(k\left(r_0+{\rho }_0\right)-\omega t\right)\right)}{2\left(r_0+{\rho }_0\right)}{\displaystyle \underset{u_1}{\overset{u_2}{\int }}\exp \left(i\frac{\pi }{2}{u}^2\right)du·{\displaystyle \underset{v_1}{\overset{v_2}{\int }}\exp \exp \left(i\frac{\pi }{2}{v}^2\right)dv}}\\ =\frac{E_m}{2}{\displaystyle \underset{u_1}{\overset{u_2}{\int }}\exp \left(i\frac{\pi }{2}{u}^2\right)du·{\displaystyle \underset{v_1}{\overset{v_2}{\int }}\exp \exp \left(i\frac{\pi }{2}{v}^2\right)dv}}\end{array}}$

Expresamos E_P en términos de las integrales de Fresnel

${\displaystyle \begin{array}{l}C(\omega )={\displaystyle \underset{0}{\overset{\omega }{\int }}\cos \left(\frac{\pi }{2}{x}^2\right)}dx,S(\omega )={\displaystyle \underset{0}{\overset{\omega }{\int }}\sin \left(\frac{\pi }{2}{x}^2\right)}dx\\ {\displaystyle \underset{0}{\overset{\omega }{\int }}\exp \left(i\frac{\pi }{2}{x}^2\right)}dx=C(\omega )+iS(\omega )\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}{E}_P=\frac{E_m}{2}\left\{C\left(u_2\right)-C\left(u_1\right)+i\left(S\left(u_2\right)-S\left(u_1\right)\right)\right\}\left\{C\left(v_2\right)-C\left(v_1\right)+i\left(S\left(v_2\right)-S\left(v_1\right)\right)\right\}\\ E_P=\frac{E_m}{2}\left\{\Delta C\left(u\right)+i\Delta S\left(u\right)\right\}\left\{\Delta C\left(v\right)+i\Delta S\left(v\right)\right\}=\\ E_P=\frac{E_m}{2}\left\{\Delta C\left(u\right)\Delta C\left(v\right)-\Delta S\left(u\right)\Delta S\left(v\right)+i\left(\Delta C\left(u\right)\Delta S\left(v\right)+\Delta S\left(u\right)\Delta C\left(v\right)\right)\right\}\end{array}}$

La intensidad en P, I_P es proporcional al cuadrado de E_P. Producto de un número complejo por su conjugado

${\displaystyle \begin{array}{l}{I}_P={\left|E_p\right|}^2=\frac{E_m^2}{4}\left\{{\left(\Delta C\left(u\right)\Delta C\left(v\right)-\Delta S\left(u\right)\Delta S\left(v\right)\right)}^2+{\left(\Delta C\left(u\right)\Delta S\left(v\right)+\Delta S\left(u\right)\Delta C\left(v\right)\right)}^2\right\}=\\ \frac{I_0}{4}\left\{\left(\Delta C{\left(u\right)}^2+\Delta S{\left(u\right)}^2\right)\left(\Delta C{\left(v\right)}^2+\Delta S{\left(v\right)}^2\right)\right\}=\\ \frac{I_0}{4}\left\{{\left(C\left(u_2\right)-C\left(u_1\right)\right)}^2+{\left(S\left(u_2\right)-S\left(u_1\right)\right)}^2\right\}\left\{{\left(C\left(v_2\right)-C\left(v_1\right)\right)}^2+{\left(S\left(v_2\right)-S\left(v_1\right)\right)}^2\right\}\end{array}}$

Cálculos y representaciones gráficas

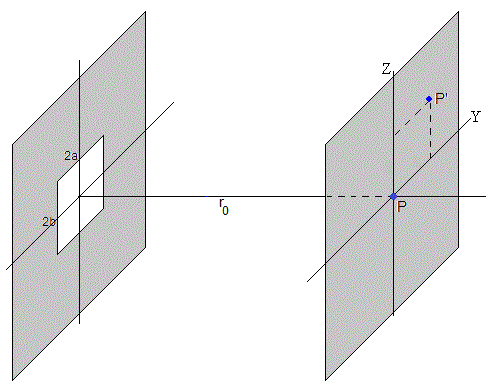
Cuando la fuente S está muy alejada ρ₀→∞. Los frentes de ondas que llegan a la abertura son planos

${\displaystyle u=y\sqrt{\frac{2}{\lambda r_0}},v=z\sqrt{\frac{2}{\lambda r_0}}}$

Los parámetros adimensionales u₁, u₂, v₁ y v₂, están relacionados con las coordenadas de la abertura rectangular y₁=-a, y₂=a, z₁=-b y z₂=b mediante el factor $f=\sqrt{\frac{2}{\lambda r_0}}$

La expresión que describe el movimiento ondulatorio en un punto P del eje de la abertura rectangular.

${\displaystyle E_P=\frac{E_m}{2}\left\{C\left(u_2\right)-C\left(u_1\right)+i\left(S\left(u_2\right)-S\left(u_1\right)\right)\right\}\left\{C\left(v_2\right)-C\left(v_1\right)+i\left(S\left(v_2\right)-S\left(v_1\right)\right)\right\}}$

Intensidad en un punto P'

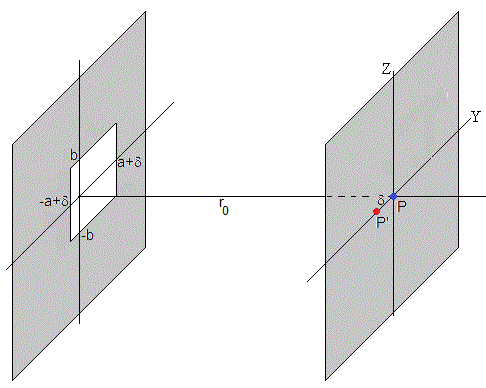
Vamos a determinar cómo se calcula E_P' para un punto P' fuera del eje. En vez de mover el punto P, la abertura rectangular se mueve en la dirección opuesta y se calcula E_P mediante la fórmula anterior

Por ejemplo, para encontrar la intensidad en el punto P' a la izquierda de P δ=1 mm, la abertura rectangular se mueve δ=1 mm hacia la derecha y se calcula la intensidad en el punto P con la nueva configuración, cambiando los valores de y₁, y₂ y consecuentemente, de u₁ y u₂. El valor calculado E_P mediante la fórmula anterior, se asigna al punto P'

• Cuando la abertura se mueve W hacia la derecha, y₂ varía desde a a a+W e y₁ desde -a a -a+W
• Cuando la abertura se mueve W hacia la arriba, z₂ varía desde b a b+W e z₁ desde -b a -b+W

La abertura rectangular es simétrica respecto de los eje Y y Z por lo que solamente hay que calcular la intensidad de los puntos situados en un cuadrante de dimensiones W×W

El código que realiza los cálculos en el primer cuadrante y representa la intensidad, siguiendo los pasos explicados en la página titulada Gráficos tridimensionales en el apartado titulado Simetría

r0=1200; %distancia abertura- pantalla en mm
l=632.8*1e-6; %longitud de onda en mm
f=sqrt(2/(l*r0)); %factor de escala 
a=0.5*f; % 2a es la achura de la abertura en mm
b=0.5*f;  % 2b es la altura de la abertura
W=2*f;  %región de pantalla
s=0.01*f; %paso

[X,Y]=meshgrid(0:s:W,0:s:W);

Cu2=fresnelc(a+X);
Cu1=fresnelc(-a+X);

Su2=fresnels(a+X);
Su1=fresnels(-a+X);

Cv2=fresnelc(b+Y);
Cv1=fresnelc(-b+Y);

Sv1=fresnels(-b+Y);
Sv2=fresnels(b+Y);

M=((Cu2-Cu1).^2+(Su2-Su1).^2).*((Cv2-Cv1).^2+(Sv2-Sv1).^2);
M=M/max(max(M));
M=flipud(M); %primer cuadrante
[m,n]=size(M);
E=zeros(m,2*n-1);
E(1:m,n:2*n-1)=M;
E(1:m,1:n-1)=fliplr(M(1:m,2:n));
F=flipud(E(1:m-1,:));
H=[E;F];

ymm=(-W:s:W)/f;
figure
[X,Y]=meshgrid(ymm,ymm);
mesh(X,Y,H);
xlabel('X')
ylabel('Y')
zlabel('In')
figure
imagesc(ymm,ymm,H,[0,1]);colormap(gray);

Ejemplos

Vamos a comprobar, cómo cambia la intensidad debida a la difracción a medida que se va incrementando la distancia r₀ de la pantalla a la abertura rectangular

• Distancia de la abertura rectangular a la pantalla, r₀=100 mm
• Longitud de onda, λ=632.8·10^-6 mm
• Dimensiones de la abertura 2a×2b, donde a=0.5 mm, b=0.5 mm
• Máximo despazamiento de la abertura, hacia la derecha y hacia arriba, W=1 mm. Dimensiones del primer cuadrante de la pantalla W×W
• Paso, s=0.01 mm

Obtenemos una representación gráfica tridimensional de la intensidad I_P en los puntos P (y,z) de la pantalla y su equivalente bidimensional en tonos de gris. Este código está adaptado de la primera referencia y es más eficiente

r0=100; %distancia abertura - pantalla en mm
l=632.8*1e-6; %longitud de onda en mm
f=sqrt(2/(l*r0)); %factor de escala 
a=0.5*f; % 2a es la achura de la abertura en mm
b=0.5*f;  % 2b es la altura de la abertura
W=1*f;  %región de pantalla
s=0.01*f; %paso

Cu2=fresnelc(a:s:W+a);
Cu1=fresnelc(-a:s:W-a);

Su2=fresnels(a:s:W+a);
Su1=fresnels(-a:s:W-a);

Cv2=fresnelc(b:s:W+b);
Cv1=fresnelc(-b:s:W-b);

Sv1=fresnels(-b:s:W-b);
Sv2=fresnels(b:s:W+b);

A=complex(Cu2-Cu1,Su2-Su1);
B=complex(Cv2-Cv1,Sv2-Sv1);
B=B';n=length(B);B=repmat(B(:,1),1,n);
A=A';A=repmat(A(:,1),1,n);A=A';

C=B*A;D=C.*conj(C);
D=D/max(max(D));
m=2*fix(((2*W)/s)/2);

E=zeros(m+1,m+1);
for q=1:1:m/2+1
    for p=1:1:m/2+1
        E(m/2+2-p,q+m/2)=D(p,q); 
    end
end
for q=m+1:-1:m/2+2
    for p=1 : 1 :m/2+1
        E(p,-q+2+m)=E(p,q);
    end
end
for q=1:1:m+1
    for p=1:1:m/2
        E(-p+2+m,q)=E(p,q);
    end
end

ymm=(-W:s:W)/f;
figure
[X,Y]=meshgrid(ymm,ymm);
mesh(X,Y,E);
xlabel('X')
ylabel('Y')
zlabel('In')
figure
imagesc(ymm,ymm,E,[0,1]);colormap(gray);
axis equal

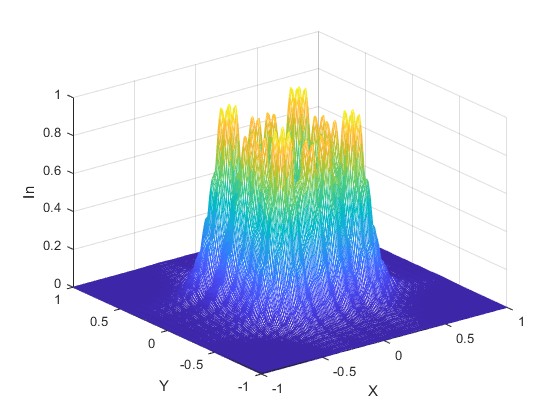
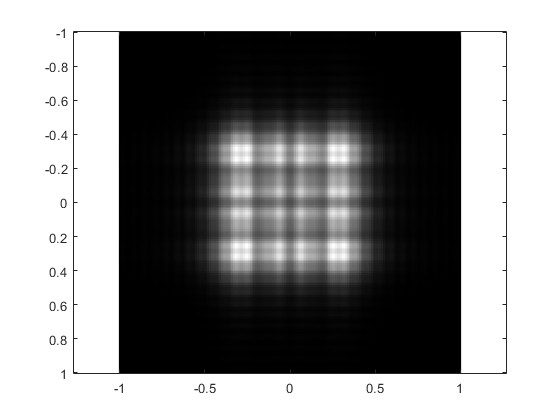
Cambiamos la distancia r₀=500 mm

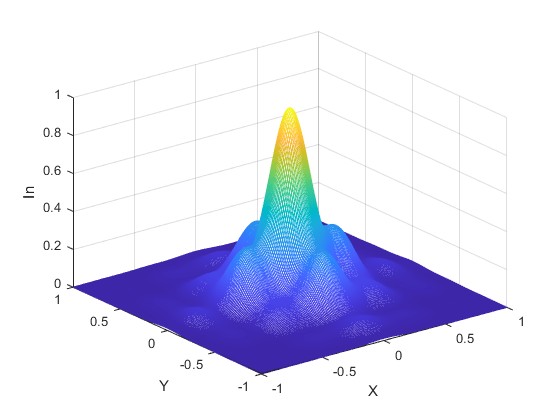
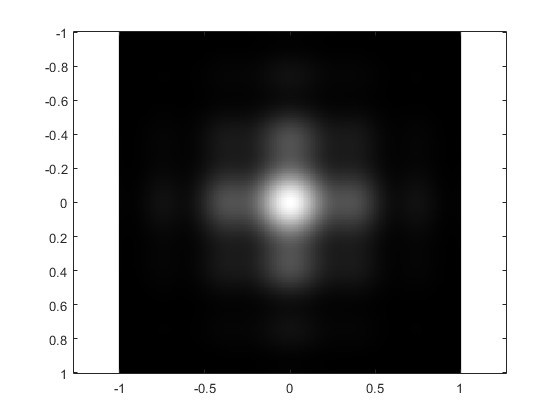
Cuando la distancia r₀=1200 mm es muy grande. Cambiamos W=2

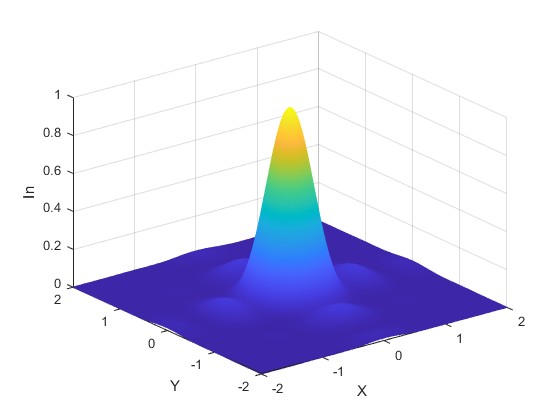
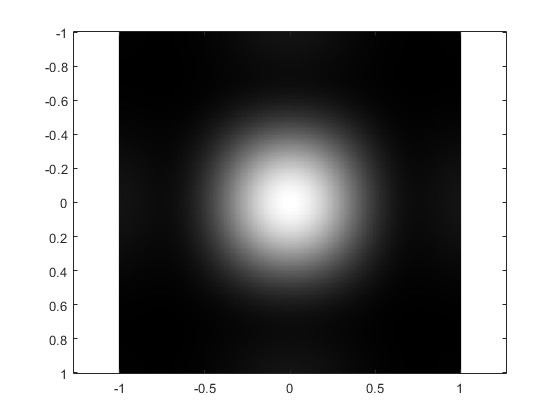
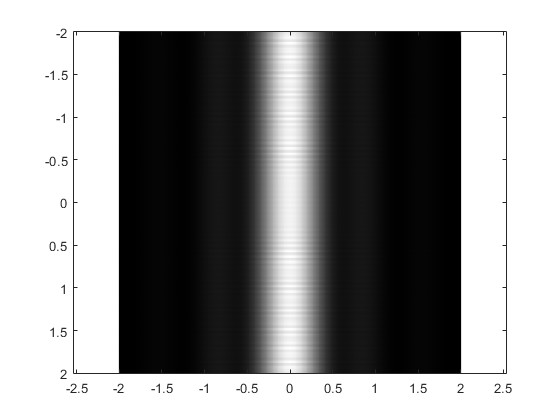
Rendija

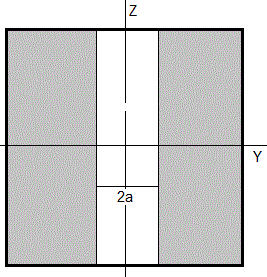
Cuando b es grande comparado con a tenemos una rendija. Sea b=10

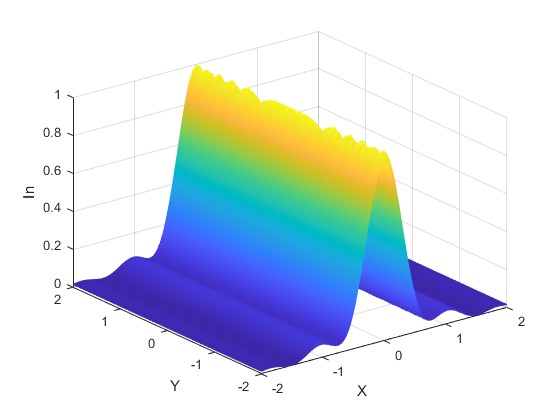
Utilizando las propiedades de las integrales de Fresnel

${\displaystyle \begin{array}{l}\underset{\omega \to \infty }{\lim }C(\omega )=\underset{\omega \to \infty }{\lim }S(\omega )=\frac{1}{2}\\ \underset{\omega \to -\infty }{\lim }C(\omega )=\underset{\omega \to -\infty }{\lim }S(\omega )=-\frac{1}{2}\end{array}}$

La intensidad en el punto P, I_P del centro de la pantalla debido a la redija de anchura 2a

${\displaystyle \begin{array}{l}{I}_P=\frac{I_0}{4}\left\{{\left(C\left(u_2\right)-C\left(u_1\right)\right)}^2+{\left(S\left(u_2\right)-S\left(u_1\right)\right)}^2\right\}\left\{{\left(\frac{1}{2}-\left(-\frac{1}{2}\right)\right)}^2+{\left(\frac{1}{2}-\left(-\frac{1}{2}\right)\right)}^2\right\}=\\ \frac{I_0}{2}\left\{{\left(C\left(u_2\right)-C\left(u_1\right)\right)}^2+{\left(S\left(u_2\right)-S\left(u_1\right)\right)}^2\right\}\end{array}}$

Vamos a comprobar, cómo cambia la intensidad debida a la difracción a medida que se va incrementando la distancia r₀ de la pantalla a la rendija

• Distancia de la rendija a la pantalla, r₀=1000 mm
• Longitud de onda, λ=632.8·10^-6 mm
• Dimensiones de la rendija 2a, donde a=0.5 mm
• Dimensiones del primer cuadrante de la pantalla W×W, W=2 mm.
• Paso, s=0.01 mm

Obtenemos una representación gráfica bidimensional, otra tridimensional de la intensidad I_P en los puntos P (y,z) de la pantalla y su equivalente bidimensional en tonos de gris.

r0=1000; %distancia rendija- pantalla
l=632.8*1e-6; %longitud de onda en mm
f=sqrt(2/(l*r0)); %factor de escala 
a=0.5*f; % 2a es la achura de la rendija
W=2*f;  %región de pantalla
s=0.01*f; %paso

Cu2=fresnelc(a:s:W+a);
Cu1=fresnelc(-a:s:W-a);

Su2=fresnels(a:s:W+a);
Su1=fresnels(-a:s:W-a);

Ip=(Cu2-Cu1).^2+(Su2-Su1).^2;
y=0:s:W;ymm=y/f;
Ipp=[fliplr(Ip),Ip];
yy=[-fliplr(ymm),ymm];

figure
plot(yy,Ipp)
grid on
xlabel('y')
ylabel('I_p')
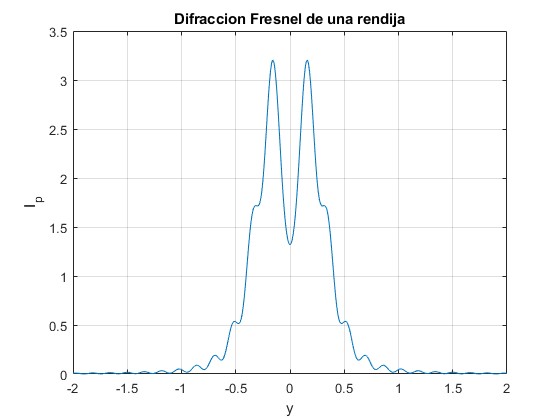
title('Difraccion Fresnel de una rendija')
Ipp=[fliplr(Ip),Ip];

figure
y=-W:s:W+s;ymm=y/f;
z=0:s:W;zmm=z/f;
E=repmat(Ipp,length(zmm),1);
[X,Y]=meshgrid(zmm,ymm);
mesh(X,Y,E');
xlabel('X')
ylabel('Y')
zlabel('In')

figure
E=E/max(max(E));
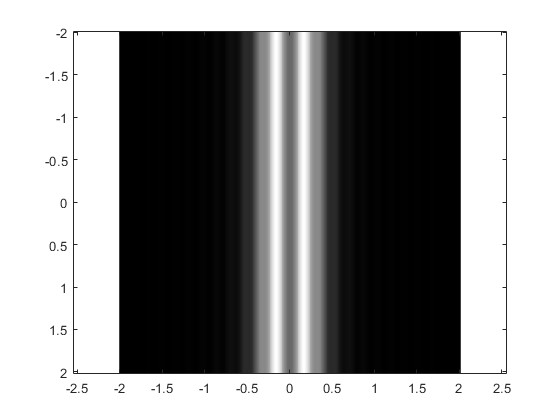
imagesc(ymm,ymm,E,[0,1]);colormap(gray);
axis equal

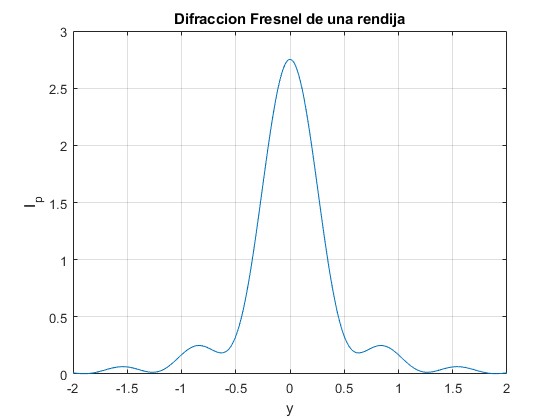
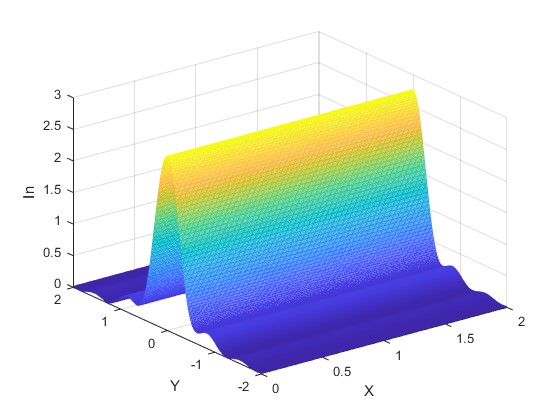
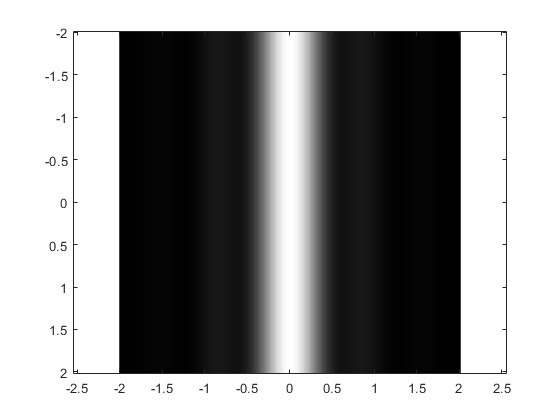
Acercamos la pantalla a la rendija, r₀=250 mm

Difracción Fraunhofer

En la teoría de la difracción Fraunhofer, se supone que las ondas incidentes son normales al plano de la rendija y que el observador se encuentra a una distancia grande en comparación con las dimensiones del obstáculo.

En la figura, se muestra el obstáculo, una abertura rectangular de lados a y b y un punto P situado en una pantalla a una distancia r₀ del obstáculo de coordenadas x e y.

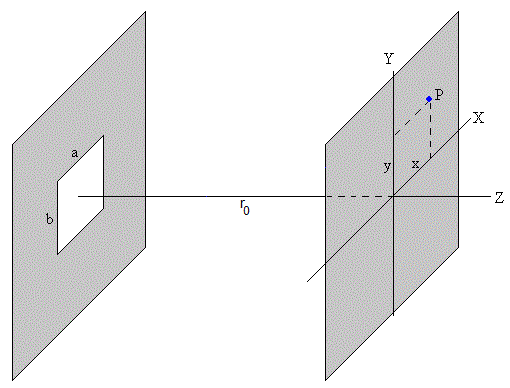
La expresión de la intensidad I(x, y) registrada en el punto P debida a la difracción de ondas planas de longitud de onda λ por el obstáculo, es

${\displaystyle I(x,y)=I(0){\left(\frac{\sin \alpha }{\alpha }\right)}^2{\left(\frac{\sin \beta }{\beta }\right)}^2\alpha =\frac{\pi a}{\lambda }\frac{x}{r_0}\beta =\frac{\pi b}{\lambda }\frac{y}{r_0}}$

Donde I(0) es la intensidad registrada en el origen x=0, y=0 de la pantalla

Actividades

Se introduce

• La longitud del lado b, en el control titulado Lado b
• La longitud del lado a, se ha fijado en a=1.0

Se pulsa el botón titulado Nuevo

Difracción Fresnel producida por dos aberturas rectangulares iguales

Sean dos aberturas rectangulares de anchura a y altura c separadas una distancia b, tal como se muestra en la figura

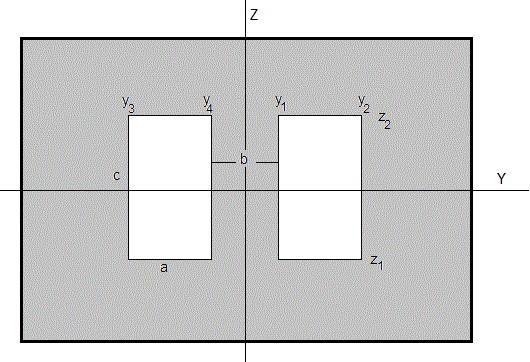
Cuando se mueven las aberturas W hacia la derecha.

• y₂ varía de a+b/2 a W+a+b/2
• y₁ varía de b/2 a W+b/2
• y₄ varía de -b/2 a W-b/2
• y₃ varía de -a-b/2 a W-a-b/2
• z₂ varía de c a W+c
• z₁ varía de -c a W-c

El movimiento ondulatorio en P es la suma de tres contribuciones: la abertura derecha y la izquierda

${\displaystyle \begin{array}{l}{E}_{P1}=\frac{E_m}{2}\left\{C\left(u_2\right)-C\left(u_1\right)+i\left(S\left(u_2\right)-S\left(u_1\right)\right)\right\}\left\{C\left(v_2\right)-C\left(v_1\right)+i\left(S\left(v_2\right)-S\left(v_1\right)\right)\right\}\\ E_{P2}=\frac{E_m}{2}\left\{C\left(u_4\right)-C\left(u_3\right)+i\left(S\left(u_4\right)-S\left(u_3\right)\right)\right\}\left\{C\left(v_2\right)-C\left(v_1\right)+i\left(S\left(v_2\right)-S\left(v_1\right)\right)\right\}\\ u=y\sqrt{\frac{2}{\lambda r_0}},v=z\sqrt{\frac{2}{\lambda r_0}}\end{array}}$

La suma es

${\displaystyle \begin{array}{l}{E}_P=E_{P1}+E_{P2}=\\ \frac{E_m}{2}\left\{C\left(u_2\right)-C\left(u_1\right)+C\left(u_4\right)-C\left(u_3\right)+i\left(S\left(u_2\right)-S\left(u_1\right)+S\left(u_4\right)-S\left(u_3\right)\right)\right\}\left\{C\left(v_2\right)-C\left(v_1\right)+i\left(S\left(v_2\right)-S\left(v_1\right)\right)\right\}\end{array}}$

La intensidad en P es

${\displaystyle I_P=\frac{E_m^2}{4}\left\{{\left(C\left(u_2\right)-C\left(u_1\right)+C\left(u_4\right)-C\left(u_3\right)\right)}^2+{\left(S\left(u_2\right)-S\left(u_1\right)+S\left(u_4\right)-S\left(u_3\right)\right)}^2\right\}\left\{{\left(C\left(v_2\right)-C\left(v_1\right)\right)}^2+{\left(S\left(v_2\right)-S\left(v_1\right)\right)}^2\right\}}$

• Distancia de la abertura rectangular a la pantalla, r₀=400 mm
• Longitud de onda, λ=500·10^-6 mm
• Dimensiones de la abertura rectangular a=0.5 mm, c= 3 mm
• Separación entre aberturas, b=2 mm
• Dimensiones del primer cuadrante de la pantalla W×W, W=4 mm.
• Paso, s=0.01 mm

r0=400; %distancia abertura- pantalla en mm
l=500*1e-6; %longitud de onda en mm
f=sqrt(2/(l*r0)); %factor de escala 
a=0.5*f; % a es la achura de la abertura en mm
b=2*f;  % b es la separación
c=3*f; %altura de la rendija
W=4*f;  %región de pantalla
s=0.01*f; %paso

Cu2=fresnelc(a+b/2:s:W+a+b/2);
Cu1=fresnelc(b/2:s:W+b/2);
Cu4=fresnelc(-b/2:s:W-b/2);
Cu3=fresnelc(-b/2-a:s:W-b/2-a);
Su2=fresnels(a+b/2:s:W+a+b/2);
Su1=fresnels(b/2:s:W+b/2);
Su4=fresnels(-b/2:s:W-b/2);
Su3=fresnels(-b/2-a:s:W-b/2-a);
A=complex(Cu2+Cu4-Cu1-Cu3,Su2+Su4-Su1-Su3);
Cv2=fresnelc(c:s:W+c);
Cv1=fresnelc(-c:s:W-c);
Sv2=fresnels(c:s:W+c);
Sv1=fresnels(-c:s:W-c);
B=complex(Cv1-Cv2,Sv1-Sv2);
B=B';n=length(B);B=repmat(B(:,1),1,n);
A=A';A=repmat(A(:,1),1,n);A=A';

C=B*A;D=C.*conj(C);
D=D/max(max(D));
m=2*fix(((2*W)/s)/2);

E=zeros(m+1,m+1);
for q=1:1:m/2+1
    for p=1:1:m/2+1
        E(m/2+2-p,q+m/2)=D(p,q); 
    end
end
for q=m+1:-1:m/2+2
    for p=1 : 1 :m/2+1
        E(p,-q+2+m)=E(p,q);
    end
end
for q=1:1:m+1
    for p=1:1:m/2
        E(-p+2+m,q)=E(p,q);
    end
end

y=-W+s:s:W-s;ymm=y/f;
figure
disp(size(E))
[X,Y]=meshgrid(ymm,ymm);
mesh(X,Y,E);
xlabel('X')
ylabel('Y')
zlabel('In')
figure
imagesc(ymm,ymm,E,[0,1]);colormap(gray);
axis equal

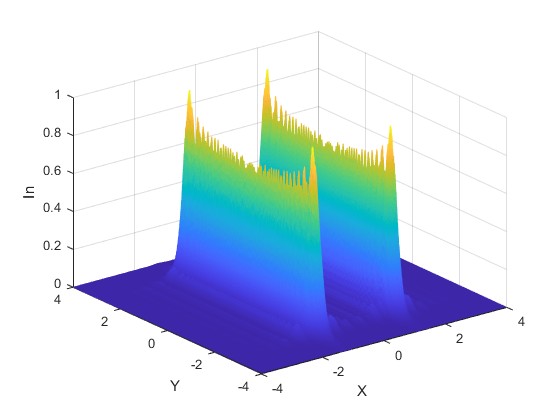
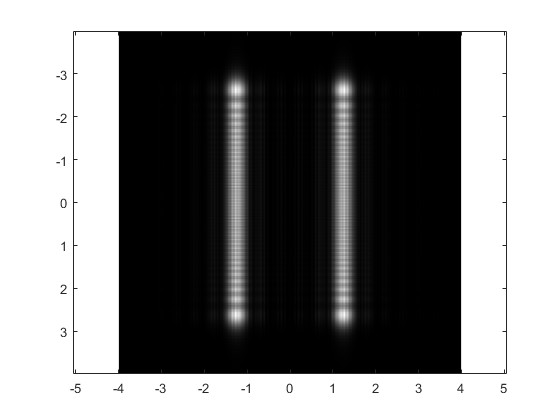
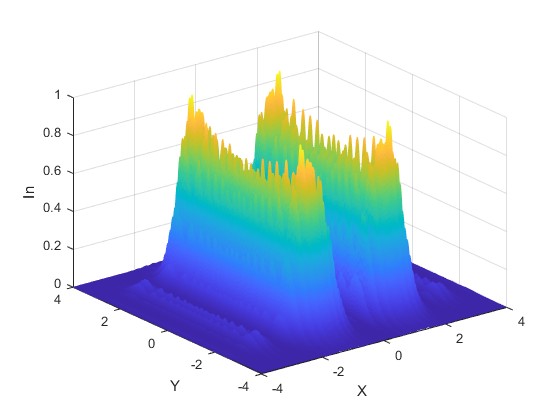
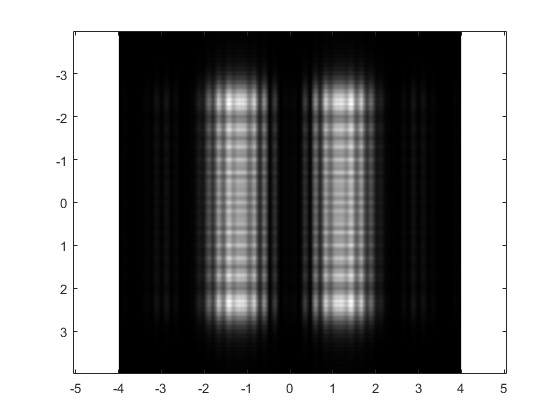
Alejamos la pantalla de las aberturas, r₀=1200 mm

Placa rectangular

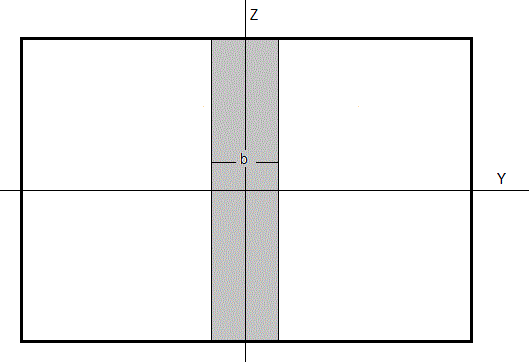
Obtenemos una placa rectangular de anchura b cuando y₃→-∞, y₂→∞. Por otra parte, z₁→-∞, z₂→∞

${\displaystyle \begin{array}{l}{E}_P=\frac{E_m}{2}\left\{\frac{1}{2}-C\left(u_1\right)+C\left(u_4\right)-\left(-\frac{1}{2}\right)+i\left(\frac{1}{2}-S\left(u_1\right)+S\left(u_4\right)-\left(-\frac{1}{2}\right)\right)\right\}\left\{\frac{1}{2}-\left(-\frac{1}{2}\right)+i\left(\frac{1}{2}-\left(-\frac{1}{2}\right)\right)\right\}=\\ \frac{E_m}{2}\left\{1-C\left(u_1\right)+C\left(u_4\right)+i\left(1-S\left(u_1\right)+S\left(u_4\right)\right)\right\}\left\{1+i\right\}\\ I_P=\frac{E_m^2}{2}\left\{{\left(1-C\left(u_1\right)+C\left(u_4\right)\right)}^2+{\left(1-S\left(u_1\right)+S\left(u_4\right)\right)}^2\right\}\end{array}}$

• Distancia de la placa a la pantalla, r₀=1000 mm
• Longitud de onda, λ=632.8·10^-6 mm
• Dimensiones de la placa b=0.5 mm
• Dimensiones del primer cuadrante de la pantalla W×W, W=4 mm.
• Paso, s=0.01 mm

Obtenemos una representación gráfica bidimensional, otra tridimensional de la intensidad I_P en los puntos P (y,z) de la pantalla y su equivalente bidimensional en tonos de gris.

r0=1000; %distancia abertura- pantalla en mm
l=632.8*1e-6; %longitud de onda en mm
f=sqrt(2/(l*r0)); %factor de escala 
b=0.5*f; % a es la achura de la placa en mm
W=4*f;  %región de pantalla
s=0.01*f; %paso

Cu1=fresnelc(b/2:s:W+b/2);
Cu4=fresnelc(-b/2:s:W-b/2);
Su1=fresnels(b/2:s:W+b/2);
Su4=fresnels(-b/2:s:W-b/2);

Ip=(Cu4-Cu1+1).^2+(Su4-Su1+1).^2;
y=0:s:W;ymm=y/f;
Ipp=[fliplr(Ip),Ip];
yy=[-fliplr(ymm),ymm];

figure
plot(yy,Ipp)
grid on
xlabel('y')
ylabel('I_p')
title('Difraccion Fresnel de una placa rectangular')
Ipp=[fliplr(Ip),Ip];

figure
y=-W:s:W+s;ymm=y/f;
z=0:s:W;zmm=z/f;
E=repmat(Ipp,length(zmm),1);
[X,Y]=meshgrid(zmm,ymm);
mesh(X,Y,E');
xlabel('X')
ylabel('Y')
zlabel('In')

figure
E=E/max(max(E));
imagesc(ymm,ymm,E,[0,1]);colormap(gray);
axis equal

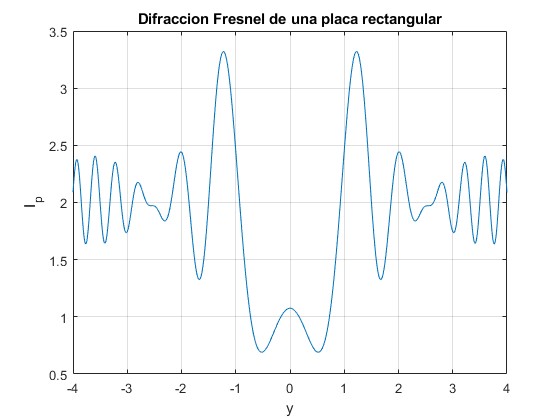
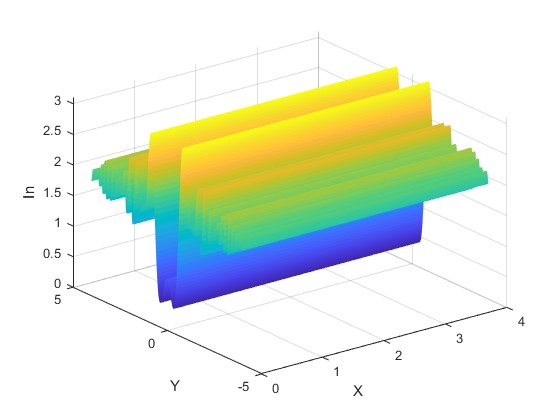
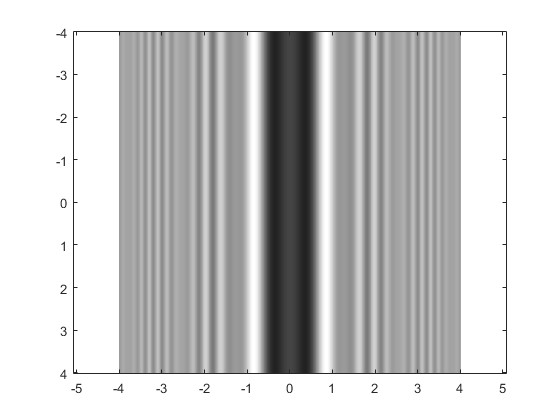
Un aspecto importante es que la intensidad en el eje Z (y=0) no es nula

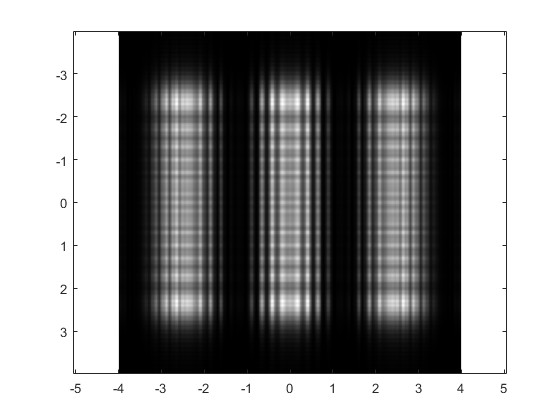
Difracción Fresnel producida por tres aberturas rectangulares iguales

Sean tres aberturas rectangulares de anchura a y altura c separadas una distancia b, tal como se muestra en la figura

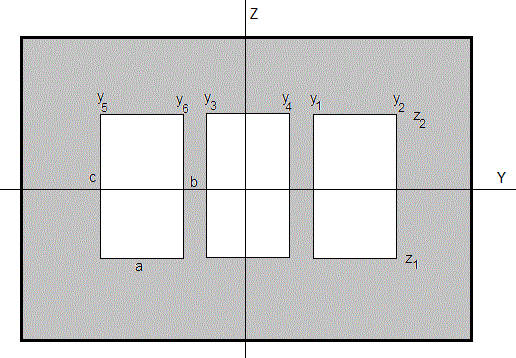
Cuando se mueven las aberturas W hacia la derecha.

• y₂ varía de 3a/2+b a W+3a/2+b
• y₁ varía de a/2+b a W+a/2+b
• y₄ varía de a/2 a W+a/2
• y₃ varía de -a/2 a W-a/2
• y₆ varía de -a/2-b a W-a/2-b
• y₅ varía de -3a/2-b a W-3a/2-b
• z₂ varía de c a W+c
• z₁ varía de -c a W-c

El movimiento ondulatorio en P es la suma de tres contribuciones: la abertura derecha, la central y la izquierda

${\displaystyle \begin{array}{l}{E}_{P1}=\frac{E_m}{2}\left\{C\left(u_2\right)-C\left(u_1\right)+i\left(S\left(u_2\right)-S\left(u_1\right)\right)\right\}\left\{C\left(v_2\right)-C\left(v_1\right)+i\left(S\left(v_2\right)-S\left(v_1\right)\right)\right\}\\ E_{P2}=\frac{E_m}{2}\left\{C\left(u_4\right)-C\left(u_3\right)+i\left(S\left(u_4\right)-S\left(u_3\right)\right)\right\}\left\{C\left(v_2\right)-C\left(v_1\right)+i\left(S\left(v_2\right)-S\left(v_1\right)\right)\right\}\\ E_{P3}=\frac{E_m}{2}\left\{C\left(u_6\right)-C\left(u_5\right)+i\left(S\left(u_6\right)-S\left(u_5\right)\right)\right\}\left\{C\left(v_2\right)-C\left(v_1\right)+i\left(S\left(v_2\right)-S\left(v_1\right)\right)\right\}\\ u=y\sqrt{\frac{2}{\lambda r_0}},v=z\sqrt{\frac{2}{\lambda r_0}}\end{array}}$

La suma es

${\displaystyle \begin{array}{l}{E}_P=E_{P1}+E_{P2}+E_{P3}=\\ \frac{E_m}{2}\left\{C\left(u_2\right)-C\left(u_1\right)+C\left(u_4\right)-C\left(u_3\right)+C\left(u_6\right)-C\left(u_5\right)+i\left(S\left(u_2\right)-S\left(u_1\right)+S\left(u_4\right)-S\left(u_3\right)+S\left(u_6\right)-S\left(u_5\right)\right)\right\}\left\{C\left(v_2\right)-C\left(v_1\right)+i\left(S\left(v_2\right)-S\left(v_1\right)\right)\right\}\end{array}}$

La intensidad en P es

${\displaystyle I_P=\frac{E_m^2}{4}\left\{{\left(C\left(u_2\right)-C\left(u_1\right)+C\left(u_4\right)-C\left(u_3\right)+C\left(u_6\right)-C\left(u_5\right)\right)}^2+{\left(S\left(u_2\right)-S\left(u_1\right)+S\left(u_4\right)-S\left(u_3\right)+S\left(u_6\right)-S\left(u_5\right)\right)}^2\right\}\left\{{\left(C\left(v_2\right)-C\left(v_1\right)\right)}^2+{\left(S\left(v_2\right)-S\left(v_1\right)\right)}^2\right\}}$

• Distancia de la abertura rectangular a la pantalla, r₀=400 mm
• Longitud de onda, λ=500·10^-6 mm
• Dimensiones de la abertura rectangular a=0.5 mm, c= 3 mm
• Separación entre aberturas, b=2 mm
• Dimensiones del primer cuadrante de la pantalla W×W, W=4 mm.
• Paso, s=0.01 mm

r0=400; %distancia abertura- pantalla en mm
l=500*1e-6; %longitud de onda en mm
f=sqrt(2/(l*r0)); %factor de escala 
a=0.5*f; % a es la achura de la abertura en mm
b=2*f;  % b es la separación
c=3*f; %altura de la rendija
W=4*f;  %región de pantalla
s=0.01*f; %paso

Cu2=fresnelc(3/2*a+b:s:W+3/2*a+b);
Cu1=fresnelc(a/2+b:s:W+a/2+b);
Cu4=fresnelc(a/2:s:W+a/2);
Cu3=fresnelc(-a/2:s:W-a/2);
Cu6=fresnelc(-a/2-b:s:W-a/2-b);
Cu5=fresnelc(-3/2*a-b:s:W-3/2*a-b);
Su2=fresnels(3/2*a+b:s:W+3/2*a+b);
Su1=fresnels(a/2+b:s:W+a/2+b);
Su4=fresnels(a/2:s:W+a/2);
Su3=fresnels(-a/2:s:W-a/2);
Su6=fresnels(-a/2-b:s:W-a/2-b);
Su5=fresnels(-3/2*a-b:s:W-3/2*a-b);
A=complex(Cu2+Cu4+Cu6-Cu1-Cu3-Cu5,Su2+Su4+Su6-Su1-Su3-Su5);
Cv2=fresnelc(c:s:W+c);
Cv1=fresnelc(-c:s:W-c);
Sv2=fresnels(c:s:W+c);
Sv1=fresnels(-c:s:W-c);
B=complex(Cv1-Cv2,Sv1-Sv2);
B=B';n=length(B);B=repmat(B(:,1),1,n);
A=A';A=repmat(A(:,1),1,n);A=A';

C=B*A;D=C.*conj(C);
D=D/max(max(D));
m=2*fix(((2*W)/s)/2);

E=zeros(m+1,m+1);
for q=1:1:m/2+1
    for p=1:1:m/2+1
        E(m/2+2-p,q+m/2)=D(p,q); 
    end
end
for q=m+1:-1:m/2+2
    for p=1 : 1 :m/2+1
        E(p,-q+2+m)=E(p,q);
    end
end
for q=1:1:m+1
    for p=1:1:m/2
        E(-p+2+m,q)=E(p,q);
    end
end
y=-W+s:s:W-s;ymm=y/f;

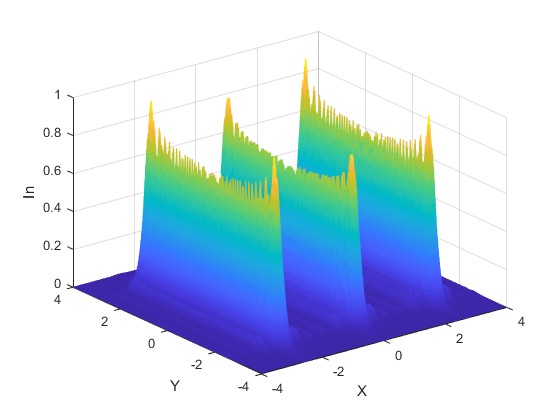
figure
[X,Y]=meshgrid(ymm,ymm);
mesh(X,Y,E);
xlabel('X')
ylabel('Y')
zlabel('In')

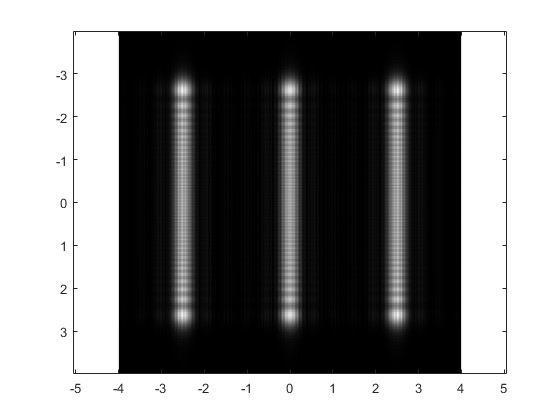
figure
imagesc(ymm,ymm,E,[0,1]);colormap(gray);

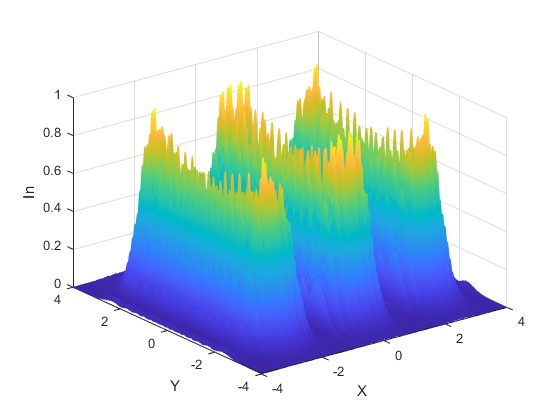
Alejamos la pantalla de las aberturas, r₀=1200 mm

Referencias

Fatema Hamid Al-Saiari, S.M. Mujibur Rahman, Kazi Monowar Abedin. Computer Simulation of Fresnel Diffraction from Triple Apertures by Iterative Fresnel Integrals Method. Archive.org

Daniel M. Reis, Edson M. Santos, A.V. Andrade-Neto. Padrão de difração de um conjunto de n fendas não simétricas e de larguras arbitrárias. Revista Brasileira de Ensino de Física, v. 37, n. 2, 2312 (2015)

K.M. Abedin, M.R. Islam, A.F.M.Y. Haider. Computer simulation of Fresnel diffraction from rectangular apertures and obstacles using the Fresnel integrals approach. ScienceDitect. Optics & Laser Technology 39 (2007) 237–246