Difracción de Fresnel

Esta página, es una aplicación de las integrales de Fresnel y de la espiral de Cornu.

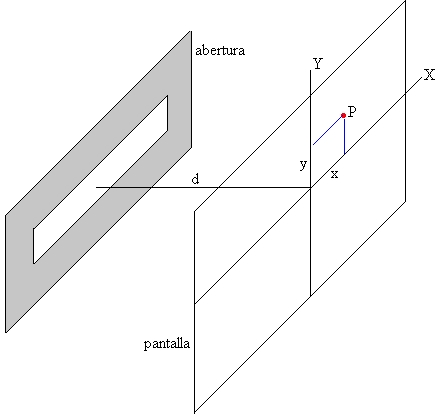
Las funciones fresnelc y fresnels de MATLAB, calculan las integrales de Fresnel C(x) y S(x), respectivamente

En los tres ejemplos, se indica el procedimiento geométrico para el cálculo de la intensidad debida a la difracción producida por

Una abertura rectangular
El borde de una placa semiinfinita
Un obstáculo en forma de placa rectangular

El último ejemplo tratado en esta página, es la difracción producida por un obstáculo en forma de placa circular, es mucho más complicado

Rendija

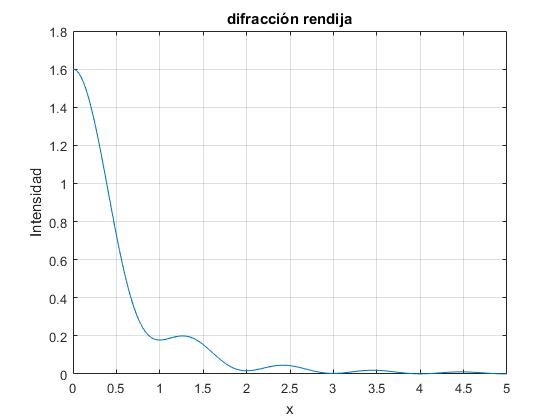
Se observa la evolución desde la difracción Fresnel a la difracción Fraunhofer a medida que se disminuye la anchura de la rendija.

dx=2; %ancho rendija
x=0:0.02:5;
s1=fresnels(x+dx/2);
s2=fresnels(x-dx/2);
c1=fresnelc(x+dx/2);
c2=fresnelc(x-dx/2);
y=((s2-s1).^2+(c2-c1).^2)/2;
plot(x,y)
grid on
xlabel('x')
ylabel('Intensidad')
title('difracción rendija')

Actividades

Se introduce la anchura de la rendija en el control titulado Ancho

Se pulsa el botón titulado Nuevo

Se mide la intensidad de la luz en una posición dada, que se puede cambiar en el control titulado Posición

Ancho:
Posición:

Borde de una placa

En el programa interactivo observamos que la intensidad no es nula en la zona de sombra de la placa y en las proximidades del borde.

Definimos una intensidad umbral como aquella I=0.01·I₀. Moviendo el pequeño cuadrado de color rojo hacia la izquierda (véase la figura más abajo) vemos que corresponde a u=2.2. (en la parte superior izquierda, se proporcionan los datos de u y de la intensidad I/I₀.

Por ejemplo, en el caso del sonido si I₀=10^-4 W/m² es decir, 80 decibeles, I=0.01·I₀=10^-6 W/m², es 60 dB.

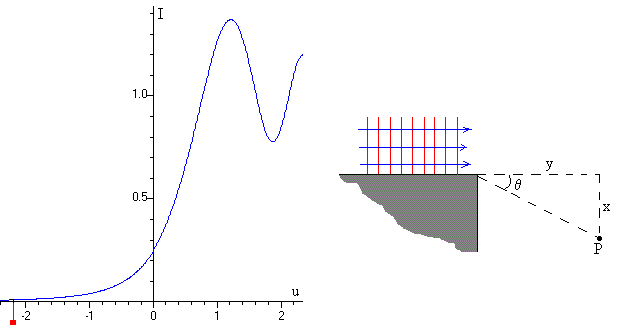
El parámetro u vale

$u = x \sqrt{\frac{2}{λ y}}$

donde x e y son las coordenadas del punto de observación P.

En la figura, se muestra el lugar geométrico de los puntos tales que u=2.2 o los puntos (x, y) para los cuales la intensidad es el 1% de la intensidad del movimiento ondulatorio que se mediría sin la presencia del obstáculo.

La curva en color rojo, se ha trazado para un movimiento ondulatorio de longitud de onda λ=0.5 m
La curva en color azul, para λ=0.1 m.

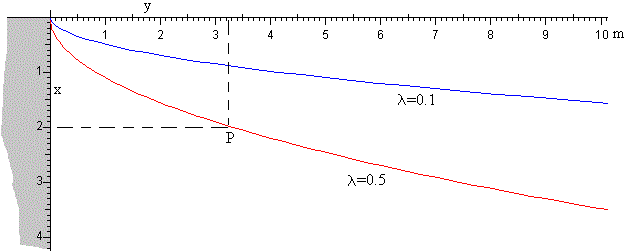
En el caso del sonido, la velocidad de propagación es 340 m/s,

Un sonido de frecuencia de 680 Hz le corresponde una longitud de onda λ=0.5 m
Un sonido de 3400 Hz le corresponde una una longitud de onda λ=0.1 m

Como apreciamos en la figura, oiremos sonido detrás de un edificio, alrededor de la esquina.

En el caso de la luz visible, su longitud de onda es del orden de λ=5·10^-7 m. La curva que se dibujaría sería indistinguible de la recta horizontal.

El sonido por tanto se difracta dentro de la región de sombra de la placa semiinfinita. En una situación real, el sonido escuchado detrás de un obstáculo puede provenir no solamente del efecto de la difracción, sino también de la reflexión por otros obstáculos que puedan estar presentes.

x=-3:0.02:5;
s=fresnels(-x);
c=fresnelc(-x);
y=((0.5-s).^2+(0.5-c).^2)/2;
plot(x,y)
grid on
xlabel('x')
ylabel('Intensidad')
title('difracción borde')

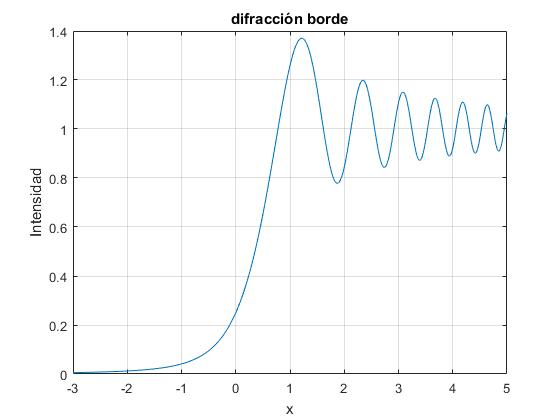
Actividades

Se mide la intensidad de la luz en una posición dada, que se establece en el control titulado Posición

Posición:

Placa rectangular

Observamos que siempre hay una región iluminada en el eje central del obstáculo

dx=2; %ancho obstáculo
x=0:0.02:5;
s1=fresnels(x+dx);
s2=fresnels(x-dx);
c1=fresnelc(x+dx);
c2=fresnelc(x-dx);
y=((1-s1+s2).^2+(1-c1+c2).^2)/4;
plot(x,y)
grid on
xlabel('x')
ylabel('Intensidad')
title('difracción obstáculo')

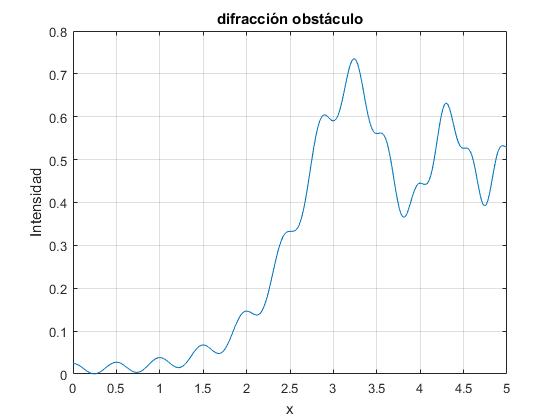
Actividades

Se introduce la anchura de la rendija en el control titulado Ancho

Se pulsa el botón titulado Nuevo

Se mide la intensidad de la luz en una posición dada, que se puede cambiar en el control titulado Posición

Ancho:
Posición:

Placa circular

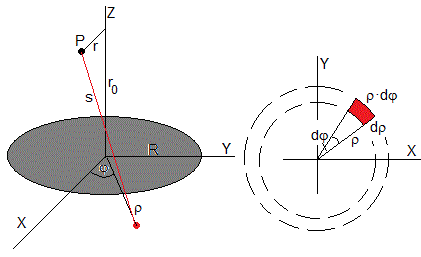
Supondremos que la distancia de la fuente de luz al obstáculo es más grande que el tamaño del obstáculo, un disco de radio R. Al plano que contiene el obstáculo llegan ondas aproximadamente planas.

El problema tiene simetría cilíndrica, por lo que bastará calcular la integral

$U (P) = A_{0} \int_{S} \frac{e^{i k s}}{s} d S$

S se refiere al área del plano que contiene el disco ρ>R, excepto el obstáculo. dS es un elemento diferencial de área en coordenadas cilíndricas que se ha pintado de color rojo en la parte derecha de la figura

En el punto de observación P dista r del eje de simetría. Suponiendo que la distancia r₀ del obstáculo al plano de observación que contiene P es grande. Hacemos las siguientes aproximaciones

$\begin{array}{l} s = \sqrt{r_{0}^{2} + {(ρ \cos φ - r)}^{2} + {(ρ \sin φ)}^{2}} = \sqrt{r_{0}^{2} + r^{2} + ρ^{2} - 2 r ρ \cos φ} \approx r_{0} + \frac{r^{2} + ρ^{2} - 2 r ρ \cos φ}{2 r_{0}} \\ \frac{1}{s} \approx \frac{1}{r_{0}} \end{array}$

>> syms x;
>> taylor(sqrt(1+x),x)
ans =(7*x^5)/256 - (5*x^4)/128 + x^3/16 - x^2/8 + x/2 + 1

El resultado es

$\begin{array}{l} U (r) \approx A_{0} \int_{R}^{\infty} \int_{0}^{2 π} \frac{e^{i k (r_{0} + \frac{r^{2} + ρ^{2} - 2 r ρ \cos φ}{2 r_{0}})}}{r_{0}} (d ρ \cdot ρ d φ) = A_{0} \frac{e^{i k r_{0}}}{r_{0}} e^{i k \frac{r^{2}}{2 r_{0}}} \int_{R}^{\infty} e^{i k \frac{ρ^{2}}{2 r_{0}}} d ρ \int_{0}^{2 π} e^{- i k \frac{r ρ \cos φ}{r_{0}}} d φ \\ U (r) \approx u_{0} (r) \int_{R}^{\infty} e^{i \frac{π ρ^{2}}{λ r_{0}}} d ρ \int_{0}^{2 π} e^{- i \frac{2 π r ρ \cos φ}{λ r_{0}}} d φ \end{array}$

La segunda integral es la función de Bessel J₀(x)

$U (r) \approx u_{0} (r) \int_{R}^{\infty} e^{i \frac{π ρ^{2}}{λ r_{0}}} J_{0} {(\frac{2 π r ρ}{λ r_{0}})}_{0} d ρ$

Como se especifica en el artículo de Kinnunen, la integral que se va a resolver es

$U (r) = \int_{R}^{\infty} e^{i \frac{π ρ^{2}}{λ r_{0}}} e^{- \frac{ρ^{2}}{σ^{2}}} J_{0} {(\frac{2 π r ρ}{λ r_{0}})}_{0} d ρ$

El límite superior ∞ se reemplaza por $\frac{λ r_{0}}{2 R} = \frac{630 \cdot 10^{- 9} \cdot 10^{3}}{2 \cdot 2 \cdot 10^{- 3}} 10^{3} = 157.5 mm$

Con los siguientes datos

Radio del disco, R=2 mm
Longitud de onda, λ=630 nm=630·10^-6 mm
Distancia desde el punto de observación al plano del disco es r₀=1 m=10³ mm
Parámetro, σ=0.015 m=15 mm

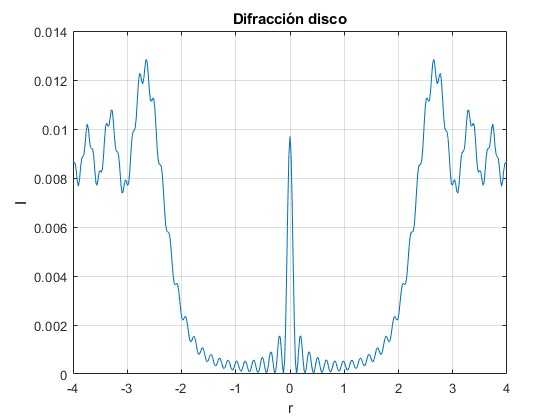
Representamos |U(r)|² en función de r en el intervalo -4, 4 mm, tendremos en cuenta que se trata de una función simétrica

rr=linspace(0,4,200);
I=zeros(1,length(rr));
k=1;
for r=rr
    f=@(x) (x.*exp(1i*pi*x.^2/0.630)).*(exp(-x.^2/15^2).*
besselj(0,2*pi*r*x/0.630));
    I(k)=abs(integral(f, 2, 157.5))^2;
    k=k+1;
end
yy=[fliplr(I),I]; %función simétrica
xx=[-fliplr(rr),rr];
plot(xx,yy)
grid on
xlabel('r')
ylabel('I')
title('Difracción disco')

Representamos |U(r)|²/|U(0)|² en el recinto cuadrado de lado 4 mm en tonos grises. Véase el apartado simetría de la página titulada Gráficos tridimensionales

Nota: este código tarda tiempo en ejecutarse

xx=linspace(0,4,200);
yy=linspace(0,4,200);
M=zeros(length(xx),length(yy));
k=1; m=1;
for X=xx
    k=1;
    for Y=yy
        r=sqrt(X^2+Y^2);
        f=@(x) (x.*exp(1i*pi*x.^2/0.630)).*(exp(-x.^2/15^2).*
besselj(0,2*pi*r*x/0.630));
        M(k,m)=abs(integral(f, 2, 157.5))^2;
        k=k+1;
    end
    m=m+1;
end
M=M/M(1,1);
M=flipud(M); %primer cuadrante
[m,n]=size(M);
E=zeros(m,2*n-1);
E(1:m,n:2*n-1)=M;
E(1:m,1:n-1)=fliplr(M(1:m,2:n));
F=flipud(E(1:m-1,:));
H=[E;F];
XX=[-fliplr(xx),xx];
YY=[-fliplr(yy),yy];
imagesc(xx,yy,H,[0,1]);colormap(gray);
axis equal

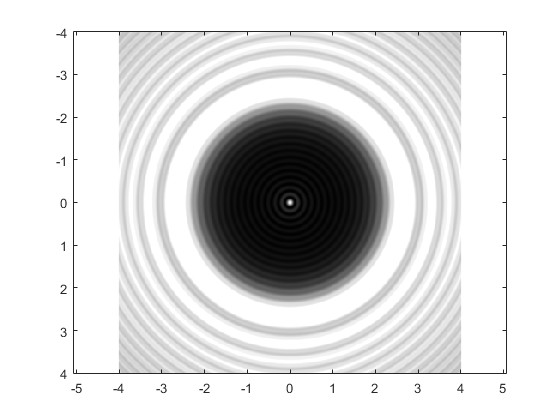
En el centro, apreciamos el punto de Arago o de Poisson

Referencias

Hecht E., Zajac A. Óptica. Editorial Addison-Wesley Iberoamericana (1986), págs. 388-418

Ferguson J. L., Why can we hear but not see around a corner?. Am. J. Phys. 54 (7) July 1986, pp. 661-662

Press W. H., Teukolsky S. A., Vetterling W. T., Flannery B. P. Numerical Recipes in C, Second edition, Special functions. Fresnel Integrals, Cosine and Sine Integrals Chapter 6º. Cambridge University Press. Código en C adaptado por el autor al lenguaje Javascript

Jami J.Kinnunen. Why is there no Poisson spot in a solar eclipse?. Am. J. Phys. 92 (12), December 2024, pp. 945–949 (2024)