Consideremos dos rendijas iguales de anchura b, separadas una distancia a tal como se indica en la figura.

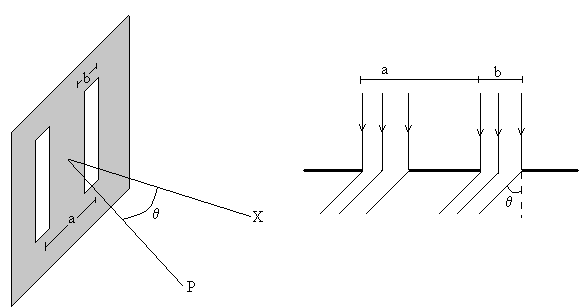
Queremos determinar la intensidad del movimiento ondulatorio en la dirección θ producida por la combinación de la interferencia de dos fuentes extensas de ondas (las rendijas) y la difracción de cada una de las rendijas.

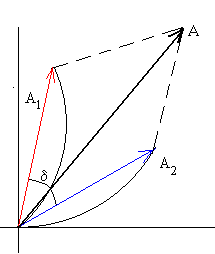
Calculamos la amplitud debida a la difracción producida por cada una de las dos rendijas..

${\displaystyle A_1=A_0\frac{\sin \left(\pi b\sin \theta /\lambda \right)}{\pi b\sin \theta /\lambda }}$

Como vimos en al estudiar la interferencia de dos fuentes, el ángulo formado por los dos vectores $\overrightarrow{A_1}$ y $\overrightarrow{A_2}$ es igual al desfase δ=k(a·sinθ)=2πasinθ/λ. Si las rendijas son iguales los módulos de los vectores son iguales A₁=A_2.

La amplitud resultante vale

${\displaystyle A=\sqrt{A_1^2+A_2^2+2A_1{A}_2\cos \delta }=2A_1\cos \left(\frac{1}{2}\delta \right)}$

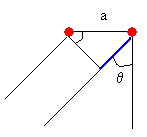
o bien,

${\displaystyle A=2A_0\frac{\text{sin}\left(\pi b\sin \theta /\lambda \right)}{\left(\pi b\sin \theta /\lambda \right)}\cos \left(\frac{\pi a\sin \theta }{\lambda }\right)}$

La intensidad que medimos en la dirección correspondiente al ángulo θ, es proporcional al cuadrado de la amplitud

${\displaystyle I=I_0{\left(\frac{\sin \left(\pi b\sin \theta /\lambda \right)}{\left(\pi b\sin \theta /\lambda \right)}\right)}^2{\cos }^2\left(\frac{\pi a\sin \theta }{\lambda }\right)}$

Si comparamos esta ecuación con la correspondiente a una rendija, vemos que ahora hay un factor adicional, un coseno cuadrado, el término que aparecía en el diagrama de interferencia de dos fuentes sincrónicas. Tenemos, por tanto, que la intensidad es el producto de dos términos

• la intensidad de la difracción producida por una rendija de anchura b,
• la intensidad debida a la interferencia de dos fuentes separadas una distancia a.

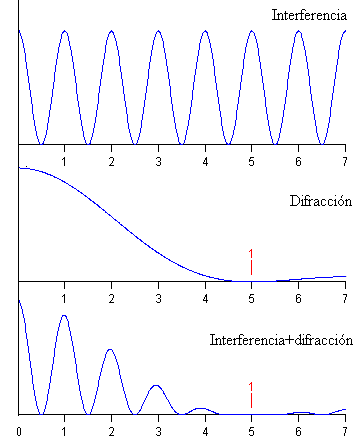
El resultado es un diagrama de interferencia modulado por el diagrama de difracción.

• Los máximos de interferencia se producen para

a·sinθ/λ=n ( n=0, ±1, ±2,…)

• Los mínimos de la intensidad debida a la difracción se producen para

b·sinθ/λ=n ( n=±1, ±2,…)

Como a>b, los ceros del diagrama de difracción están más espaciados que los máximos del diagrama de interferencia, tal como puede apreciarse en la figura.

Redes de difracción

El siguiente paso, es considerar el diagrama de difracción producido por varias rendijas paralelas de igual ancho b, espaciadas regularmente una distancia a.

La intensidad que medimos en la dirección correspondiente al ángulo θ es el producto de dos términos:

• la intensidad de la difracción producida por una rendija de anchura b,
• la intensidad debida a la interferencia de N fuentes separadas una distancia a.

${\displaystyle I=I_0{\left(\frac{\sin \left(\pi b\sin \theta /\lambda \right)}{\left(\pi b\sin \theta /\lambda \right)}\right)}^2{\left(\frac{\sin \left(N\pi a\sin \theta /\lambda \right)}{\sin \left(\pi a\sin \theta /\lambda \right)}\right)}^2}$

El diagrama consistirá en una serie de franjas brillantes, correspondientes a los máximos principales de la interferencia de N fuentes dada por

a·sinθ/λ=n  con n=0, ±1, ±2,…

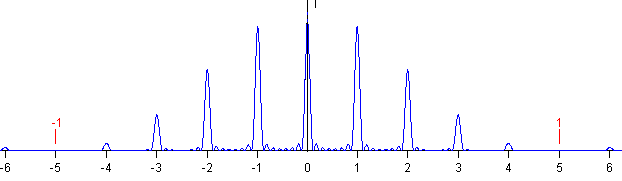
pero los valores de estos máximos estarán moduladas por el diagrama de difracción, tal como puede verse en la figura. Los mínimos de difracción están señalados en color rojo.

Actividades

Se introduce

• La anchura b de la rendija en mm, en el control titulado Anchura.
• La separación a entre dos rendijas consecutivas en mm, en el control titulado Separación. La separación tiene que ser mayor que la anchura a>b.
• El número N de rendijas, eligiendo un número en el control titulado Número de fuentes.

1. Si se activa el botón de radio titulado Interferencia, se representa el diagrama de interferencia producido por N fuentes separadas una distancia a.
2. Si se activa el botón de radio titulado Difracción se representa el diagrama de difracción correspondiente a una rendija de anchura b.
3. Si se activa el botón de radio titulado Interferencia + Difracción, se representa el diagrama de interferencia modulado por el diagrama de difracción.

Se pulsa el botón titulado Nuevo.

En la parte inferior, se representa la intensidad codificada en colores pertenecientes a la escala de grises. El color blanco indica máxima intensidad y el negro intensidad nula.

En la parte superior, se traza el diagrama de intensidad en función de x=a·sinθ/λ, se marca sobre el diagrama en color rojo los mínimos de difracción.

Ejemplo:

• Anchura de la rendija, b=0.2 mm

• Separación entre rendijas, a=1.0 mm

• Número de rendijas, N=2.

Posición x=2.0, que corresponde a un máximo de interferencia

Si a·sinθ/λ=x entonces  b·sinθ/λ=xb/a

En la fórmula de la intensidad ponemos a·sinθ/λ=2.0, y b·sinθ/λ=0.4

El valor de la intensidad es

${\displaystyle \frac{I}{I_0}={\left(\frac{\sin \left(\pi ·0.4\right)}{\left(\pi ·0.4\right)}\right)}^2{\left(\frac{\sin \left(2\pi ·2.0\right)}{\sin \left(\pi ·2.0\right)}\right)}^2={0.76}^2·1^2=0.57}$

Si la longitud de onda λ=650 nm=650·10^-9 m entonces la dirección de observación corresponde a un ángulo tal que sinθ=x·λ/a =0.001  es decir, θ=0.07º

Red de difracción girada

Supondremos una red de difracción formada por rendijas paralelas separadas la misma distancia a

La red de difracción se puede girar un ángulo α en el sentido contrario a las agujas del reloj o en el mismo sentido

Giro en sentido contrario a las agujas del reloj

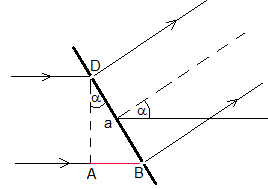
Consideremos dos rendijas adyaccentes B y D separadas a. La diferencia de caminos entre las dos ondas que interfieren es AB (señalado en color rojo)

${\displaystyle a\sin \alpha =n_0\lambda }$

Por ejemplo, sea una red de difracción de 300 rejillas/mm iluminada con luz de longitud de onda λ=650 nm. La red ha sido girada α=75°.

Despejamos n₀=4.9535

• Direcciones de máxima de intensidad (interferencia constructiva), para n>n₀



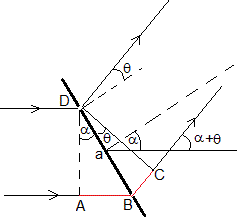
Consideremos dos rendijas adyaccentes A y D. La diferencia de caminos entre las dos ondas que interfieren es AB+BC (señalado en color rojo)

Las direcciones α+θ de máxima intensidad son

${\displaystyle \begin{array}{l}a\sin \alpha +a\sin \theta =n\lambda ,n>n_0\\ \theta =\arcsin \left(n\frac{\lambda }{a}-\sin \alpha \right),n<n_m\end{array}}$

Donde n es un entero mayor que n₀

El número entero n se ha de mantener menor que un máximo n_m, cuando el argumento de arcsin se hace mayor que uno. Con los datos del ejemplo, el máximo valor de n es 10

• Direcciones de máxima de intensidad (interferencia constructiva), para 0≤n<n₀



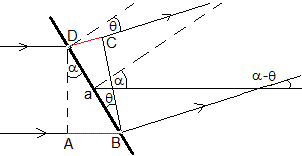
Consideremos dos rendijas adyaccentes A y D. La diferencia de caminos entre las dos ondas que interfieren es AB-CD (señalado en color rojo)

Las direcciones α-θ correspondientes a la interferencia constructiva son

${\displaystyle \begin{array}{l}a\sin \alpha -a\sin \theta =n\lambda ,0\le n<n_0\\ \theta =\arcsin \left(\sin \alpha -n\frac{\lambda }{a}\right)\end{array}}$

Donde n es un entero positivo o nulo menor que n₀

Cuando n=0, la dirección del máximo de intensidad es α-θ=0

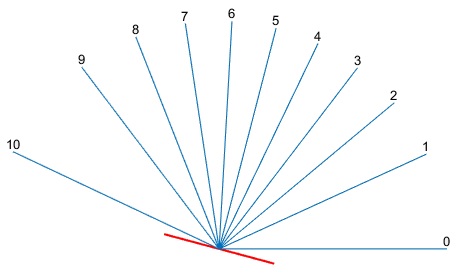
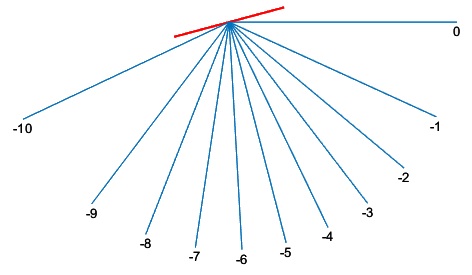
Representamos las direcciones en las que se produce interferencia constructiva

d=1e-3/300; %distancia etre rendijas
lambda=650e-9; %longitud de onda
alfa=75*pi/180; %ángulo de la red
n0=d*sin(alfa)/lambda;
r=0.5;
s=2;
line([-r*sin(alfa),r*sin(alfa)],[r*cos(alfa),-r*cos(alfa)],
'lineWidth',1.5,'color','r')
n_max=floor((1+sin(alfa))*d/lambda);
for n=floor(n0)+1:n_max
    th=asin(n*lambda/d-sin(alfa));
    line([0,s*cos(alfa+th)],[0,s*sin(alfa+th)])
    text(s*cos(alfa+th),s*sin(alfa+th),num2str(n),'HorizontalAlignment',
'center','VerticalAlignment','bottom')
end
for n=0:floor(n0)
    th=asin(sin(alfa)-n*lambda/d);
    line([0,s*cos(alfa-th)],[0,s*sin(alfa-th)])
    text(s*cos(alfa-th),s*sin(alfa-th),num2str(n),'HorizontalAlignment',
'center','VerticalAlignment','bottom')
end
grid on
axis equal
axis off

Giro en sentido de las agujas del reloj

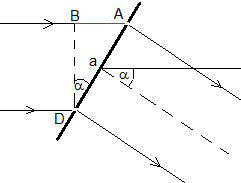
Consideremos dos rendijas adyaccentes B y D separadas a. La diferencia de caminos entre las dos ondas que interfieren es AB (señalado en color rojo)

${\displaystyle a\sin \alpha =n_0\lambda }$

El ángulo α es negativo y n₀ también

Con los datos del ejemplo, cuando la red ha sido girada α=-75°.

Despejamos n₀=-4.9535

• Direcciones de máxima de intensidad (interferencia constructiva), para n<n₀



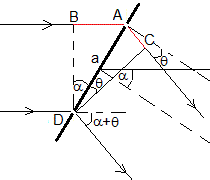
Consideremos dos rendijas adyaccentes A y D. La diferencia de caminos entre las dos ondas que interfieren es BA+AC (señalado en color rojo)

Las direcciones α+θ correspondientes a la interferencia constructiva son

${\displaystyle \begin{array}{l}a\sin \alpha -a\sin \theta =n\lambda ,0\le n<n_0\\ \theta =\arcsin \left(\sin \alpha -n\frac{\lambda }{a}\right)\end{array}}$

El ángulo θ es negativo, y el ángulo de desviación es α+θ

El número entero n se ha de mantener mayor que un mínimo n_m, cuando el argumento de arcsin se hace menor que menos uno. Con los datos del ejemplo, el mínimo valor de n es -10

• Direcciones de máxima de intensidad (interferencia constructiva), para 0≥n>n₀



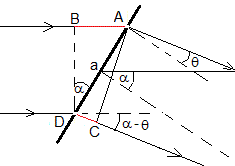
Consideremos dos rendijas adyaccentes A y D. La diferencia de caminos entre las dos ondas que interfieren es AB-CD (señalado en color rojo)

Las direcciones α-θ correspondientes a la interferencia constructiva son

${\displaystyle \begin{array}{l}a\sin \alpha -a\sin \theta =n\lambda ,0\ge n>n_0\\ \theta =\arcsin \left(\sin \alpha -n\frac{\lambda }{a}\right)\end{array}}$

Donde n es un entero negativo o nulo mayor que n₀

Cuando n=0, la dirección del máximo de intensidad α-θ=0

Representamos las direcciones en las que se produce interferencia constructiva

d=1e-3/300; %distancia etre rendijas
lambda=650e-9; %longitud de onda
alfa=-75*pi/180; %ángulo de la red
n0=d*sin(alfa)/lambda;
r=0.5;
s=2;
line([r*sin(alfa),-r*sin(alfa)],[-r*cos(alfa),r*cos(alfa)],
'lineWidth',1.5,'color','r')
n_max=floor((-1+sin(alfa))*d/lambda);
for n=n_max+1:floor(n0)
    th=asin(n*lambda/d-sin(alfa));
    disp(th)
    line([0,s*cos(alfa+th)],[0,s*sin(alfa+th)])
    text(s*cos(alfa+th),s*sin(alfa+th),num2str(n),'HorizontalAlignment',
'center','VerticalAlignment','top')
end
for n=floor(n0)+1:0
    th=asin(sin(alfa)-n*lambda/d);
    line([0,s*cos(alfa-th)],[0,s*sin(alfa-th)])
    text(s*cos(alfa-th),s*sin(alfa-th),num2str(n),'HorizontalAlignment',
'center','VerticalAlignment','top')
end
grid on
axis equal
axis off

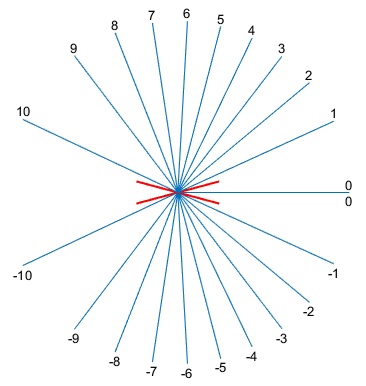
Juntamos las dos figuras para apreciar la simetría.

Dirección mínima

Representamos la dirección α-θ del máximo de intensidad para n<n₀

${\displaystyle \begin{array}{l}a\sin \alpha -a\sin \theta =n\lambda ,0\le n<n_0\\ \alpha -\theta =\alpha -\arcsin \left(\sin \alpha -n\frac{\lambda }{a}\right)\end{array}}$

d=1e-3/300; %distancia etre rendijas
lambda=650e-9; %longitud de onda
n=2;
f=@(alfa) alfa-asin(sin(alfa)-n*lambda/d);
hold on
fplot(f,[0,pi/3])
alfa_m=asin(n*lambda/(2*d));
plot(alfa_m,f(alfa_m),'ro','markersize',3,'markerfacecolor','r')
hold off
grid on
set(gca,'XTick',0:pi/12:pi/3)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3'})
xlabel('\alpha')
ylabel('\alpha-\theta')
title('n=2')

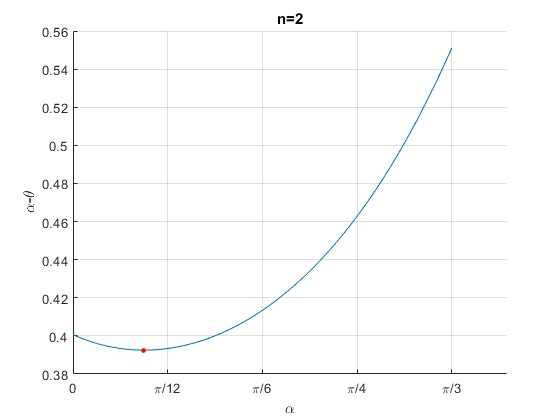
La función α-θ tiene un mínimo señalado por un punto de color rojo

${\displaystyle \begin{array}{l}\frac{d\left(\alpha -\theta \right)}{d\alpha }=1-\frac{\cos \alpha }{\sqrt{1-{\left(\sin \alpha -n\frac{\lambda }{a}\right)}^2}}=0\\ 1-{\left(\sin \alpha -n\frac{\lambda }{a}\right)}^2={\cos }^2\alpha \\ \sin {\alpha }_m=\frac{n}{2}\frac{\lambda }{a}\\ \sin {\theta }_m=-\frac{n}{2}\frac{\lambda }{a}\\ {\alpha }_m-{\theta }_m=2\arcsin \left(\frac{n}{2}\frac{\lambda }{a}\right)\end{array}}$

Para el ángulo girado α_m, la dirección del máximo de intensidad correspondiente a n<n₀, es α_m-θ_m

Referencias

Hui Peng. Math Model of Rotating Grating —CW/CCW Rotation Angle-Dependence. 2022. hal-03603596