Oszilazioak |
Osziladore akoplatuak
|
Ikasgelako erakustaldia | |
Ikasgelako erakustaldia
Handik gutxira, pendulu gorria erabat geldizen da, eta pendulu urdinak anplitude maximoa dauka. Ondoren, jokabideak berriz ere trukatzen hasten dira: pendulu urdinaren anplitudea gutxituz eta gorriarena handituz. Jokabideok energiaren ikuspegitik aztertzen badira, ikusten da, energia pendulu batetik bestera aldatuz doala. Akoplamendua ahula bada, kasu honetan bezala, bi penduluen energien batura konstantea izan behar da. Higiduraren ekuazioakBi osziladore akoplatu aztertzeko, har dezagun eregu gisa, bi partikulaz osaturiko sistema, biak m masadunak, eta biak malguki banatan lotuta. Bi malgukien konstante elastikoak berdinak dira eta ezagunak: k. Akoplamendua adierazteko, elkar ditzagun bi partikulak beste hirugarren malguki batez: kc konstanteduna, irudiak erakusten duen bezala: |
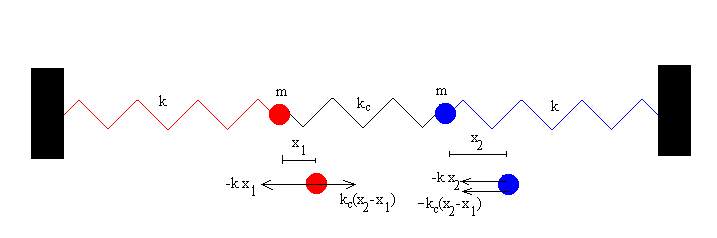 |
Dei diezaiegun x1 eta x2
bi partikulen desplazamenduei, oreka-posizioekiko (goiko irudian,
oreka-posizioan daude eta behekoan desplazatuta). Desplazamenduak
positiboak dira eskumara direnean eta alderantziz. Demagun ezkerreko
malgukia x1 distantzia luzatuta dagoela (eskumara) eta
eskumako malgukia berriz, zapalduta, x2 distantzia
(eskumara). Beraz, erdiko malgukiaren deformazioa hau izango da: x2-x1.
(Irudian suposatu dugu x2 handiagoa dela x1
baino, beraz, erdiko malgukia luzatuta dagoela) Partikulek jasaten dituzten
indarrak irudian erakusten dira.
Erdiko malgukiak egiten dituen bi indarrak berdinak eta aurkakoak dira, eta bakoitza partikula batean aplikatzen da. Partikula bakoitzari Newton-en bigarren legea aplikatzen badiogu eta higidura-ekuazioak bigarren ordenako ekuazio diferentzial gisa idazten baditugu:
Egiten bada, ekuazio diferentzial bien batura edo kenketa Higidura Harmoniko Sinplearen ekuazioa ateratzen da, kasu batean zein bestean.
Beraz bi higidura harmoniko sinple ateratzen dira; hona hemen euren maiztasun angeluarrak:
Bi ekuazio horien soluzioak honela idatz daitezke: ya=x1+x2=y0a sin(wat+ja) Hemen y0a eta y0b anplitudeak dira, eta ja eta jb hasierako faseak. Lauak hasierako baldintzetatik determinatzen dira, alegia, partikula bakoitzaren posizioetatik eta abiaduretatik. Aurreko bi ekuazioetatik x1 eta x2 bakan daitezke:
Bi osziladore akoplaturen higidura orokorra kontsidera daiteke bi modu normalen gainezartze gisa, batak wa maiztasun angeluarra du eta besteak wb . Hasierako baldintzakDei diezaiegun partikulen posizioei t=0 aldiunean, x01 eta x02. Eta demagun hasieran biak pausagunean daudela. Zenbait buruketa egin ondoren bi ekuazioak honela berridazten dira:
Bibrazioaren modu normalakwa maiztasun angeluarrari modu normal bat dagokio. Hori gertatzen da bi osziladoreak fasean mugitzen direnean edo x01 eta x02 berdinak direnean. Orduan, erdiko malgukia ez da inoiz deformatzen eta beraz, ez die indarrik egiten bi partikulei. Partikulok akoplatuta egongo ez balira bezala mugitzen dira:
Bigarren modu normalak wb maiztasun angeluarra dauka. Hori gertatzen da bi osziladoreak "aurkako fasetan" mugitzen direnean, edota x01 = - x02 denean. Osziladore bakoitzaren higidura ekuazioak, kasu horretan, honela idatz daitezke:
Orokorrean, edozein baldintzatan, osziladoreak bi modu horien nahasketaz mugituko dira. Ikasgelako erakustaldiaren simulazioaIkasgelako erakustaldian x02 nulua da. Partikulen higidura-ekuazioak modu sinpleagoan idatz daitezke, honako erlazio trigonometrikoak aplikatzen badira: cosA+cosB eta cosA-cosB.
Osziladore baten anplitudea aldakorra bada, anplitude modulatu deritzo. Bi osziladoreek anplitude modulatuak dituzte. Lehen osziladorearen anplitudea hau da: x01·cos(wa-w b)·t /2 , eta bigarren osziladorearen anplitudea: x01·sin(wa-w b)·t /2. Lehen osziladorearen anplitudea (kosinu funtzioa) aurreratuta dago (p/2) bigarren osziladorearen anplitudearekiko, eta horregatik ematen dio energia osziladore batek besteari eta gero alderantziz. Periodo-laurden batean, lehenak bigarrenari energia ematen dio, bere anplitudea gutxituz eta bestearena handituz. Bigarren laurdenean, ordea, alderantziz gertatzen da. Prozesua behin eta berriz errepikatzen da etengabe. Energiaren ikuspegiaKalkula dezagun sistemaren energia totala: bi partikulen energia zinetikoen batura eta hiru malgukien energia potentzialen batura. Ezkerreko malgukiaren deformazioa x1 da, eskumakoarena x2 eta erdikoarena x2-x1.
Terminoak bildu ondoren, lehen parentesian x1 aldagaia soilik agertzen da, eta horregatik dei diezaiokegu, lehen osziladorearen energia. Bigarren terminoak soilik du x2-ren menpekotasuna eta, horregatik, bigarren osziladorearen energia deituko diogu. Hirugarren eta azken terminoak, berriz, x1 eta x2-ren menpekotasuna dauka eta akoplamenduaren energia deituko diogu. Termino honek deskribatzen du bi osziladoreen arteko energia-trukea. SaiakuntzaAukeran idatz daitezke:
Hasi botoia sakatu. Bibrazioaren modu normalak
Ikasgelako erakustaldia simulatzea
|