Oszilazioak

Osziladoreak (I)

Oszilazio askeak

Oszilazio indargetuak

Oszilazio behartuak:
egoera iraunkorra

Oszilazio behartuak:
egoera iragankorra

Pohl-en pendulua

Partikula bat malguki
baten gainera erori

Kutxa bat, garraio
zinta baten gainean

Indar konstante
batek indargetutako
osziladorea (I)

Indar konstante
batek indargetutako
osziladorea (II)

Higiduraren ekuazioak

Saiakuntza

Erreferentziak

Lehenago ikusi den osziladore harmoniko indargetuan, marruskadura-indarra abiaduraren proportzionala da, eta honako ezaugarri nagusiak ditu:

1. Anplitudea esponentzialki gutxitzen doa denborarekiko.

2. Osziladoreak, teorikoki, denbora infinitua behar du guztiz gelditzeko.

Aldiz, indar konstante batek indargetutako osziladoreak beste honako ezaugarriak ditu:

1. Anplitudea gutxitzen doa, baina kantitate konstante bat oszilazio-erdi bakoitzean.

2. Guztiz gelditzen da denbora finitu batean.

Osziladore harmonikoa aztertuko dugu, baina irristatzearen aurkako marruskadura indarraren eraginpean. Marruskadura-indar horrek modulu konstantea dauka, baina noranzkoa beti da abiaduraren aurkakoa.

Demagun bloke bat, gainazal horizontal batean etzanda eta malguki baten muturrean lotuta. Blokearen masa m, malgukiaren konstantea k, eta marruskadura koefiziente estatiko eta zinetikoak hurrenez hurren μ_s eta μ_k, baina sinplifikatzeko: μ=μ_s = μ_k.

Har dezagun posizioaren jatorritzat (x=0) malgukiaren oreka-posizioa. Blokea oreka-posiziotik aterako dugu, x₀ posizioraino, eta askatu egingo dugu abiadurarik gabe.

Sistema horren portaera aztertuko dugu, lehenik, energiaren ikuspegitik eta, ondoren, higiduraren ekuazio diferentzialak ebatzita.

Energiaren ikuspegia

Blokearen energia totala (zinetikoa gehi potentziala) gutxituz joango da, marruskadura-indarrak lana egiten duelako.

Kalkula ditzagun, lehenik, zein posiziotan gelditzen den blokea (v=0). Posizio horiei itzultze-posizio deritze, bertan gelditu eta aurkako noranzkoan abiatzen delako. Azkenik, horietako batean, blokea gelditu egingo da. Blokearen abiadurak nuluak direnez, bai hasierako posizioan zein amaierako posizioan, energiaren balantzea honela idazten da:

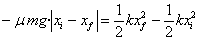
Hemen x_i hasierako posizioa da eta x_f  amaierakoa.

Defini dezagun parametro berri bat, a parametroa:

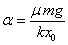
1. Hasierako posizioa: x₀

Blokea ezkerrerantz abiatuko da, malgukiak egiten dion indarra (kx₀) marruskadura-indarra baino handiagoa baldin bada (μmg). Bestela blokea geldi geratuko da. Demagun mugitzeko baldintza betetzen dela: μmg ≤  kx₀  edota  α≤1.

2. Lehen gelditze-posizioa, x₁

Energiaren balantzea honela idazten da:

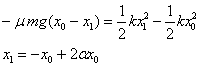
• Baldin 1/2 ≤ α ≤ 1, orduan blokea ez da jatorrira iritsiko, eta lehenago geldituko da x₁≥0.

• Baldin α < 1/2, orduan blokea jatorriraino iritsiko da, gaindituko du eta x₁<0 beste itzultze-posizio bat izango da (adibidez, marruskadurarik gabe, a=0, eta blokea −x_o posizioraino iritsiko da, justu posizio simetrikoraino).

Demagun bigarren kasua gertatzen dela: x₁<0 irudiak erakusten duen bezala:

3. Bigarren gelditze-posizioa, x₂

Blokea x₁ posiziotik abiatuko da, honako baldintza betetzen bada: k|x₁|≥ μmg,

k(x₀-2αx₀)≥ μmg edota α ≤ 1/3 bestela x₁ posizioan gelditu egingo da. Demagun lehen baldintza betetzen dela:

Energiaren balantzea honela idazten da:

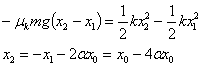
• Baldin 1/4 ≤ α ≤ 1/3, orduan blokea ez da jatorriraino iritsiko, lehenago geldituko da, eta  x₂≤0  amaierako posizioa izango da.

• Baina α<1/4 bada, orduan, blokea jatorriraino iritsiko da, gaindituko du eta x₂>0 beste itzultze-posizio bat izango da.

Demagun bigarren kasua gertatzen dela, x₂>0, irudiak erakusten duen bezala:

4. Hirugarren gelditze-posizioa: x₃

Blokea x₂ posiziotik abiatuko da, honako baldintza betetzen bada: kx₂≥ μmg,

k(x₀-4αx₀)≥ μmg  edota  α≤1/5, bestela x₂ posizioan geldituko da. Demagun lehen baldintza betetzen dela:

Energiaren balantzea honela idazten da:

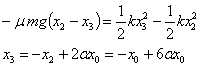
• Baldin 1/6≤α≤1/5, orduan blokea ez da jatorriraino iritsiko eta bere amaiera x₃≥0  posizioan gertatuko da.

• Baina  α<1/6 bada, blokea jatorriraino iritsiko da, gainditu eta itzultze posizioa izango du honako posizioan: x₃<0

x₃ positiboa bada, hortxe amaituko da ibilbidea, baina negatiboa bada, mugitzen jarraituko du, behin eta berriz, orain arte bezala.

Orokorrean.

Orokorrean, honela idatz daiteke n-garren gelditze-posizioa:

x_n=(-1)ⁿ(1-2nα)x₀

• Baldin  1/(2n)≤α≤1/(2n-1), blokea ez da jatorriraino iritsiko, eta bertan geldituko da, x_n posizioan.

• Baina  α<1/(2n) bada, blokeak jatorria gaindituko du eta  x_n itzultze-posizioa izango da.

α parametroaren arabera, blokea geldituko da n-garren gelditze-posizioan eta:

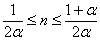
Adibidea:

• Demagun k =50, m=1, eta μ=0.7,

• Hasierako posizioa x₀=0.7 eta pausagunetik abiatuz.

Kalkula dezagun lehenik a parametroa:

• Egiaztatzen da hasieran ez dela geldi geratuko: kx₀≥ μmg, 50·0.7>0.7·1·9.8

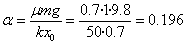
Kalkula dezagun lehen gelditze-posizioa: x₁

x₁=-x₀+2αx₀=-0.7+2·0.1372·0.7= -0.4256

negatiboa denez, jatorritik ezkerrera dago.

• Egiaztatzen da posizio horretan ez dela geldi geratuko:  k|x₁|≥ μmg, 50·0.4256>0.7·1·9.8

Eta bigarren gelditze-posizioa kalkulatzen da: x₂

x₂=x₀-4αx₀= 0.1512

Posizio positiboak, jatorritik eskumara dagoela adierazten du.

• Egiaztatzen da posizio horretan ere ez dela geldi geratzen: kx₂≥ μmg, 50·0.1512>0.7·1·9.8

Kalkula dezagun hirugarren gelditze-posizioa: x₃

x₃= -x₀+6αx₀= 0.1232

Positiboa denez, jatorritik eskumara dago, eta eskumatik zetorrenez, bere azken oszilazioan ez da jatorriraino iritsi. Beraz, bertan geldituko da.

Egiazta daiteke:

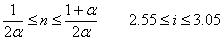
Betetzen dela baldin n=3.

Energiaren Balantzea

Guztira blokeak ibili duen distantzia guztiz gelditu den arte:

s₃=x₀+2|x₁|+2x₂+|x₃| = x₀+2(x₀-2αx₀)+2(x₀-4αx₀)+(x₀-6αx₀)

Eta orokorrean:

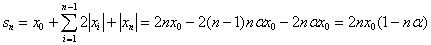
zeren n-1 zenbaki bikoitiren batura hau baita: (n-1)·n

Marruskadura-indarrak egindako lana:

W_r= -μmg·s_n= - μmg (1-nα)·(2n·x₀)

Eta malgukiaren energia potentzialaren aldakuntza:

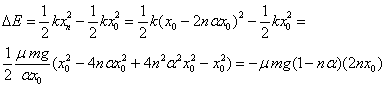
Ikusten denez, berdinak dira:  W_r=ΔE

Higiduraren ekuazioak

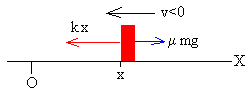	Blokea ezkerrerantz mugitzen ari denean (v<0), higiduraren ekuazioa honela idazten da: ma= -kx+ μmg,
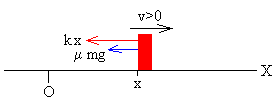	Aldiz, blokea eskumarantz mugitzen ari denean, (v>0), higiduraren ekuazioa honela idazten da: ma= -kx- μmg,

Marruskadura indarrak noranzkoa aldatzen du, beti abiaduraren aurka. Higiduraren ekuazioak ekuazio diferentzial gisa idatzita:

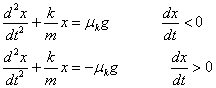
Ekuazio horiek Higidura Harmoniko Sinplearen ekuazio diferentzialaren itxura dute, baina termino gehigarri bat dute: ±μ_kg

Ekuazio diferentzial horren soluzioak bi zati ditu: batetik, ekuazio homogeneoaren soluzioa (termino gehigarririk gabe HHS-aren soluzio bera) eta bestetik, konstante bat (x=C, termino gehigarria konstantea delako). C konstantea determinatzen da, konstantea bera ekuazio diferentzial osoan ordezkatuz:

(k/m)C= ±μ_kg,     C= ±μ_kmg/k= ±αx₀

Beraz, ekuazio diferentzial bien soluzio osoak honela idatz daitezke:

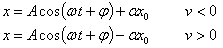
Soluzio horiek ekuazio diferentzialak betetzen dituzte, hurrenez hurren, eta bertan ordezkatuz egiazta daitezke.

Bi kasuetan blokearen abiadura ere kalkula daiteke:

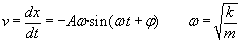
A eta φ konstanteak hasierako baldintzetatik determinatzen dira

1. Hasierako posizioa: x₀

Blokea ezkerrerantz abiatzen da (v<0) malgukiaren indarrak, kx₀ , marruskadura gainditzen badu, μmg , bestela geldi geratuko da.

Demagun abiatzeko gai dela: kx₀≥ μmg.

Hona hemen hasierako baldintzak: t=0 aldiunean, abiadura nulua, v=0, eta posizioa: x=x₀.

x₀=A₁cosφ+αx₀
0=A₁ω·sinφ

Hortaz blokearen posizioa denboraren menpe honela geratzen da:

x=A₁cos(ωt)+αx₀,  eta anplitudea hau da: A₁= x₀ -αx₀.
Beraz,  x=(x₀-αx₀)cos(ωt)+αx₀

Blokearen abiadura honela adierazten da:

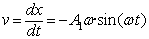
Eta lehen gelditze-posizioraino iristean, x₁, abiadura baliogabetzen da, alegia ωt=π denean.

Blokearen posizioa aldiune horretan:

x₁= -(x₀-αx₀)+αx₀ = -x₀+2αx₀

Izan ere, aurreko atalean, energiaren ikuspegitik emaitza bera lortu dugu.

2. Blokea eskumarantz mugitzen da: v>0

Blokea eskumarantz abiatuko da malgukiaren indarrak marruskadura gainditzen badu: k|x₁|≥ μmg . Bestela geldi geratuko da. Demagun abiatzeko gai dela:

Hona hemen hasierako baldintzak: ωt=π aldiunean, abiadura nulua da, v=0, eta posizioa, x₁.

x₁=A₂cos(π+φ)-αx₀
0=A₂ω·sin(π+φ)

Blokearen posizioa denboraren menpe honela adieraz daiteke:

x=A₂cos(ωt)-αx₀,  eta anplitudea hau da: A₂=-x₁-αx₀=x₀-3αx₀
x=(x₀-3αx₀)cos(ωt)-αx₀

Blokearen abiadura honela adierazten da:

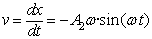
Eta hurrengo gelditze-posiziora iristen denean, x₂, abiadura baliogabetzen da, alegia ωt=2π denean.

x₂=A₂-αx₀ =x₀-4αx₀

Izan ere, aurreko atalean, energiaren ikuspegitik emaitza bera lortu dugu.

Prozesu guztia jarraitu behar da blokea gelditzen den arte.

Laburpena

Blokeak oszilazio guztiak periodo berarekin betetzen ditu:

• Lehen oszilazio erdian, v<0, hau da blokearen posizioa denboraren menpe:

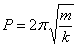
x=(x₀-αx₀)·cos(ωt)+αx₀,

• Bigarren oszilazio erdian, berriz, v>0, blokearen posizioa denboraren menpe:

x=(x₀-3αx₀)cos(ωt)-αx₀

• Orokorrean, n-garren oszilazio erdian, blokearen posizioa eta abiadura honela adierazten dira denboraren menpe:

x=x₀(1-(2n-1) α)·cos(ωt)-(-1)ⁿ·αx₀
v=-x₀(1-(2n-1) α)·ωsin(ωt)

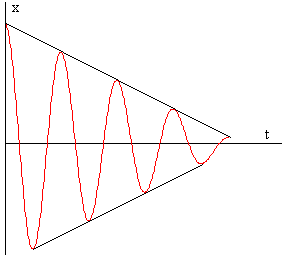Oszilazio erdi bakoitzean blokea mugitzen da HHS-arekin eta anplitude konstantearekin. Oszilazio erdi batetik hurrengora, alegia, gelditze-posizio bakoitzaren ondoren, energia gutxitu egiten da kantitate konstante bat: 2αx0. Desplazamendu maximoak lotuz, zuzen bi ateratzen dira honako maldarekin: ±4αx0/P (eta horrek badauka antza marruskadura likatsuan (biskosoan) ateratzen diren inguratzaile esponentzial biekin. Gelditze-posizioak honako aldiuneetan gertatzen dira: tn= n·π/ω   n=1, 2, 3,..

Adibidea:

• Demagun k =50, m=1, eta μ=0.7.

Oszilazioen maiztasun angeluarra ateratzen da: ω=7.07 rad/s, eta periodoa P=0.89 s.

• Hasierako posizioa: x₀=0.7 eta abiadura nulua.

1. Egiazta dezagun blokea abiatzeko gai dela, alegia, malgukiaren indarrak marruskadura gainditzen duela: kx₀≥ μmg, 50·0.7>0.8·1·9.8

Lehen oszilazio erdiaren anplitudea hau da: A₁=x₀-αx₀ =0.5628

Blokea ezkerrerantz abiatzen da (v<0) eta bere posizioa denboraren menpe:

x=0.5628·cos(7.07·t)+0.1372

Blokearen abiadura:

v= -0.5628·7.07·sin(7.07·t)

Abiadura nulu bilakatzen denean, ωt=π, orduan t=0.44.

Aldiune horretan blokearen posizioa: x₁= -0.5628+0.1372= -0.4256

Eta posizio hori jatorritik ezkerrera dago.

2. Egiazta dezagun gelditze-posizio horretan malgukiaren indarrak marruskadura gainditzen duela:  k|x₁|≥ μmg, 50·0.4256>0.7·1·9.8, beraz, blokea eskumarantz abiatuko da.

Bigarren oszilazio erdiaren anplitudea kalkula dezagun: A₂=A₁-2αx₀ = 0.2884

Blokea eskuinerantz desplazatzen da (v>0) eta  bere posizioa denboraren menpe:

x=0.2884·cos(7.07·t)-0.1372

Blokearen abiadura:

v= -0.2884·7.07·sin(7.07·t)

Abiadura nulu bilakatzen da honako aldiunean: ωt=2π, eta orduan t=0.89.

Kalkula dezagun bigarren gelditze-posizioa:  x₂= 0.2884-0.1372= 0.1512

Eta posizio hori jatorritik eskumara dago.

3. Egiazta dezagun gelditze-posizio horretan malgukiaren indarrak marruskadura gainditzen duela: kx₂≥ μmg, 50·0.1512>0.7·1·9.8. beraz, blokea ezkerrerantz abiatuko da (v<0).

Hirugarren oszilazio erdiaren anplitudea kalkula dezagun:

A₃=A₂-2αx₀= 0.014

Blokea ezkerrerantz abiatzen da (v<0) eta bere posizioa denboraren menpe:

x=0.014·cos(7.07·t)+0.1372

Blokearen abiadura:

v= -0.014·7.07·sin(7.07·t)

Abiadura nulu bilakatzen da honako aldiunean: ωt=3π,eta orduan t=1.33.

Kalkula dezagun hirugarren gelditze-posizioa: x₃= -0.014+0.1372= 0.1232

eta hori jatorritik eskumara dago, beraz ez da jatorriraino iritsi. Horixe izango da amaiera.

 

Saiakuntza

Aukeran idatz daitezke:

• Marruskadura koefizientea, m, desplazamendu-barrari saguaz eragiten.

• Malgukiaren konstante elastikoa, k , dagokion kontrolean idatziz.

• Blokearen masa finkotzat hartzen da: m=1.0 kg

Berria botoia sakatu.

• Saguarekin, blokea mugi daiteke hasierako posiziora: x₀ jatorritik eskumara.

Hasi botoia sakatu.

Blokea mugitzen ikusten da, malgukiaren eraginez, atzera eta aurrera irristatzen, gelditze-posizioen artean, guztiz gelditzen den arte.

Grafiko batek blokearen posizioa adierazten du denboraren menpe.

• Gezi gorri batek malgukiaren indarra adierazten du.

• Gezi urdin batek marruskadura-indarra adierazten du.

Leihatilaren eskumako eta goiko aldean programak idatziz erakusten ditu honako datuak:

• Denbora.

• Blokearen posizioa.

• Blokearen abiadura.

• Blokearen energia totala (zinetikoa gehi potentziala).

Leihatilaren ezkerraldean blokearen energia adierazten da barra-diagrama batez.

• Gorriz, energia potentzial elastikoa.

• Urdinaz, energia zinetikoa.

ikusten denez, energia totala gutxituz doa marruskaduraren eraginez.

Kalkula bitez gelditze-posizioak datu jakin batzuekin, eta gero konpara bitez programa interaktiboak ematen dituenekin.