Figuras de Lissajous
Compondremos dos M.A.S de direcciones perpendiculares dados por las ecuaciones
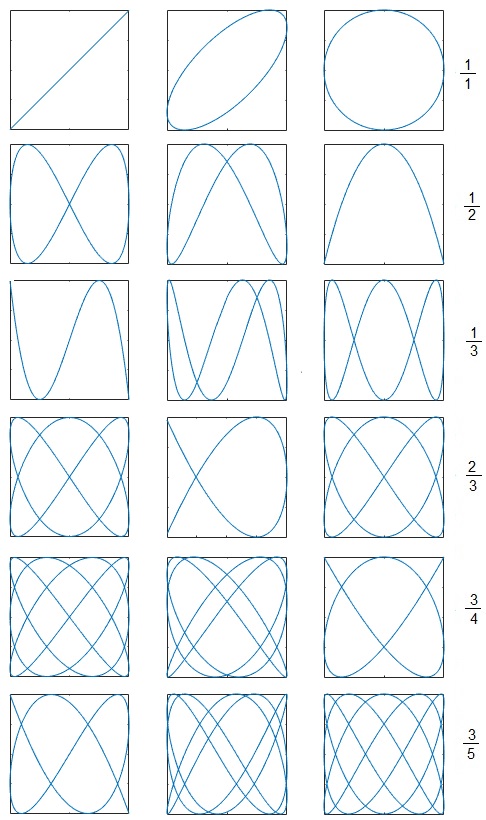
Las amplitudes son Ax y Ay, las frecuencias angulares ωx y ωy, respectivamente, y δ es la diferencia de fase entre ambos movimientos. En la representación gráfica, las filas son ωx/ωy=1/1, 1/2, 1/3, 2/3, 3/4, 3/5, para la diferencia de fase δ=0, π/4 y π/2 (columnas)
wx=3; %frecuencia en eje X wy=5; %frecuencia en el eje Y subplot(1,3,1) delta=0; %desfase fplot(@(t) sin(wx*t), @(t) sin(wy*t+delta), [0,2*pi]) axis square subplot(1,3,2) delta=pi/4; fplot(@(t) sin(wx*t), @(t) sin(wy*t+delta), [0,2*pi]) axis square subplot(1,3,3) delta=pi/2; fplot(@(t) sin(wx*t), @(t) sin(wy*t+delta), [0,2*pi]) axis square
Composición
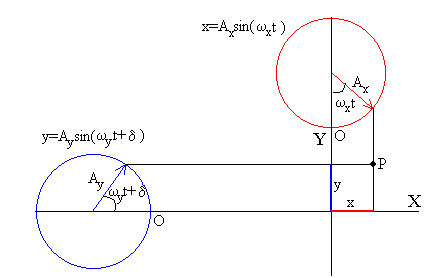
La composición de dos M.A.S. de direcciones perpendiculares se obtiene a través de la relación existente el M.A.S y el movimiento circular uniforme.
El primer M.A.S. se origina proyectando el extremo del vector rotatorio Ax sobre el eje X, el segmento marcado en color rojo. Al girar con velocidad angular ωx, al cabo de un cierto tiempo t, su posición angular es ωxt. El origen de ángulos se encuentra en el punto marcado por O.
El segundo M.A.S. se origina proyectando el extremo del vector rotatorio Ay sobre el eje Y, el segmento marcado en color azul. Al girar con velocidad angular ωy, al cabo de un cierto tiempo t, su posición angular es ωyt+δ. El origen de ángulos se encuentra en el punto marcado por O y δ es la posición angular de partida en el instante t=0.
Actividades
Se introduce
- la frecuencia angular del primer M.A.S. (eje X), en el control titulado Frecuencia angular X
- la frecuencia angular del segundo M.A.S. (eje Y), en el control titulado Frecuencia angular Y
- la diferencia de fase (en grados) entre los dos M.A.S, en el control titulado Diferencia de fase
Se pulsa el botón titulado Nuevo.
Se sugieren los siguientes ejemplos:
| Frecuencia (X) | Frecuencia (Y) | Diferencia de fase |
|---|---|---|
| 1 | 1 | 0 |
| 1 | 1 | 90 |
| 1 | 1 | 180 |
| 1 | 1 | 270 |
| 1 | 2 | 0 |
| 1 | 2 | 90 |
| 2 | 1 | 0 |
| 2 | 1 | 90 |
| 2 | 3 | 0 |
| 2 | 3 | 90 |
Otra forma de ver las figuras de Lissajous, similar a la que se observa en un osciloscopio
Figuras de Lissajous no periódicas
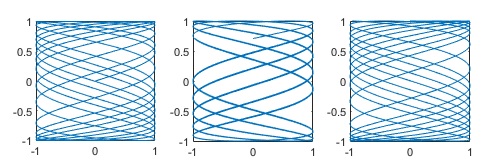
Componemos dos MAS con amplitudes Ax=1, Ay=1, frecuencias angulares, ωx=π, ωy=1 con los desfases, δ=0, π/4 y π/2
wx=pi; %frecuencia en eje X wy=1; %frecuencia en el eje Y subplot(1,3,1) delta=0; %desfase fplot(@(t) sin(wx*t), @(t) sin(wy*t+delta), [0,10*pi]) axis square subplot(1,3,2) delta=pi/4; fplot(@(t) sin(wx*t), @(t) sin(wy*t+delta), [0,10*pi]) axis square subplot(1,3,3) delta=pi/2; fplot(@(t) sin(wx*t), @(t) sin(wy*t+delta), [0,10*pi]) axis square
Figuras de Lissajous tridimensionales
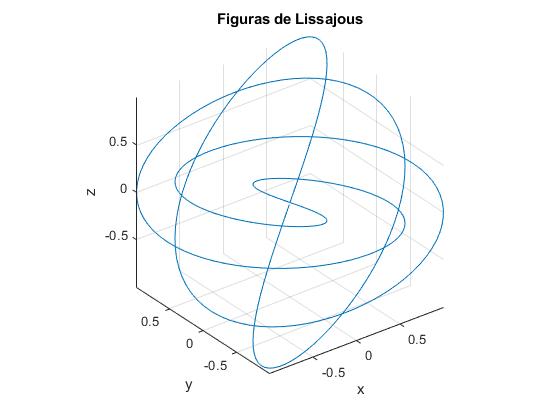
Componemos tres MAS con amplitudes Ax=1, Ay=1, Az=1, frecuencias angulares, ωx=5, ωy=3, ωz=4 con los desfases, δy=0, δz=0
wx=5; %frecuencia en eje X
wy=3; %frecuencia en el eje Y
wz=4; %frecuencia en el eje Z
delta_y=0; %desfase
delta_z=0; %desfase
t=0:0.02:2*pi;
x=sin(wx*t);
y=sin(wy*t+delta_y);
z=sin(wz*t+delta_z);
plot3(x,y,z)
grid on
axis equal
xlabel('x'); ylabel('y'); zlabel('z')
title('Figuras de Lissajous')
Medida de la frecuencia y del desfase de dos señales
Las trayectorias del movimiento resultante de componer dos M.A.S. de direcciones perpendiculares se denomina figuras de Lissajous, tales trayectorias dependen de la relación de frecuencias angulares ωx/ωy y de la diferencia de fase.
Medida del desfase entre dos señales
Componemos dos MAS de direcciones perpendiculares y de la misma frecuencia angular ω, desfasados δ . Supondremos que ambas señales tiene la misma amplitud A.
x=A·sin(ω·t)
y=A·sin(ω·t+δ )
La trayectoria es una elipse.
La medida de la intersección de la elipse con los ejes X e Y nos permite medir el desfase δ, entre dos señales x e y.
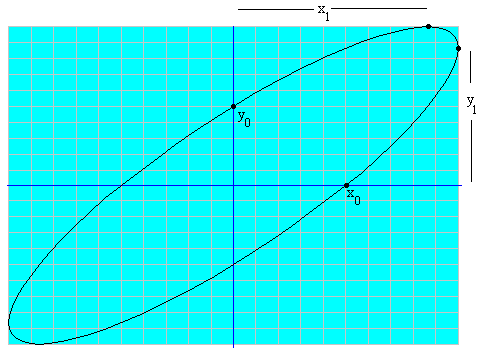
Intersección con el eje Y
Intersección con el eje X
Intersección con x=A el borde derecho de la pantalla del "osciloscopio"
Cuando x=0, entonces ω·t=0, ó π.
y0=A·sinδ
y0=A·sin(π+δ )=-A·sinδ
Si medimos en la parte positiva del eje Y, tendremos que sin δ=y0/A
En la pantalla del "osciloscopio" el eje X y el eje Y está dividido en 20 partes, cada división es una unidad.
Ejemplo: en la figura, A=10, e y0=5, el desfase δ=30º, ó mejor δ=π/6
Cuando y=0, entonces ω·t=-δ , ó π-δ .
x0=-A·sinδ
x0=A·sin(π-δ )=A·sinδ
Ejemplo: en la figura, A=10, e x0=5, el desfase δ=30º, ó mejor δ=π/6
A=A·sin(ω·t) por lo que ω·t=π/2
y1=A·sin(π/2+δ)=A·cosδ
Ejemplo: en la figura A=10 y y1=8.75, el desfase δ≈30º, ó mejor δ=π/6
Se obtiene la misma trayectoria con el desfase 30º y 330º y también con 150º y 210º. Pero podemos distinguir el desfase 30º de 150º, por la orientación de los ejes de la elipse.
Medida de la frecuencia
Componemos dos MAS de direcciones perpendiculares y de distinta frecuencia angular ωx, y ωy .Supondremos que ambas señales tiene la misma amplitud A y el desfase δ puede ser cualquier valor
x=A·sin(ωx·t)
y=A·sin(ωy·t+δ)
La relación de frecuencias angulares se puede obtener a partir del número de tangentes de la trayectoria en el lado vertical y en el lado horizontal.
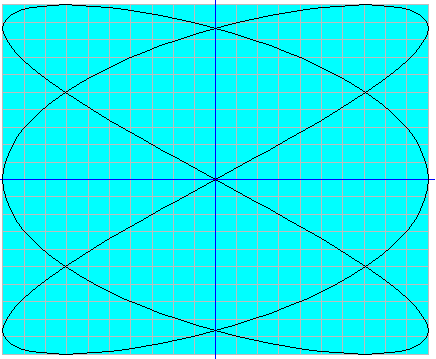
Ejemplo: en la figura
Composición de funciones periódicas
No solamente la función seno o coseno es periódica, podemos crear nuestras funciones periódicas tal como se describe en la página titulada Otras funciones
En este apartado, vamos de representar las figuras de Lissajous que se obtendrían con otras funciones periódicas distintas de las armónicas
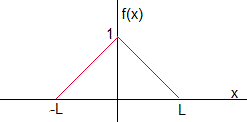
Consideremos la función f(x) definida en el intervalo (-Lx, Lx), la hacemos periódica de periodo 2Lx denominando a esta función Fx(x)
Consideremos otra función g(x) definida en el intervalo (-Ly, Ly), la hacemos periódica de periodo 2Ly denominando a esta función Fy(x)
Vamos a ver cual es el resultado de la composición de las dos funciones periódicas Fx(x) y Fy(x+δ). Donde δ es el desfase
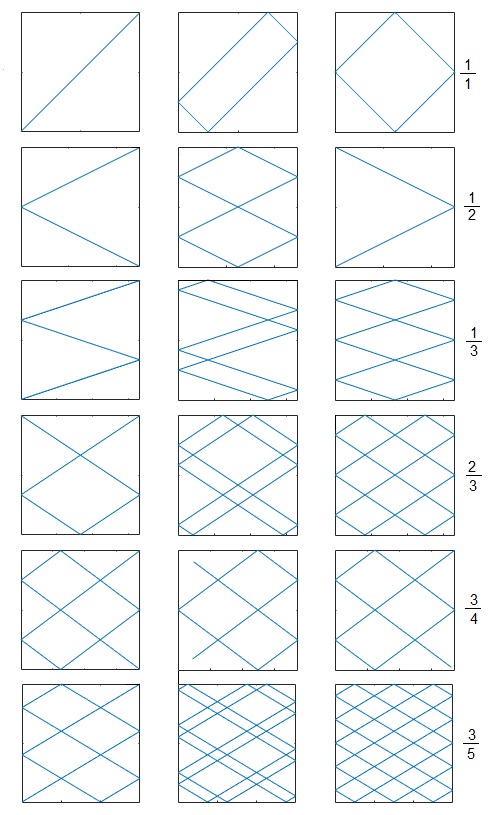
En la representación gráfica, las filas son Lx=m/n=1/1, 1/2, 1/3, 2/3, 3/4, 3/5, Ly=1. La diferencia de fase δ= 0, 1/4, 1/2 (columnas)
m=3; %mumerador n=5; %denominador L=m/n; %función periódica 2L por el ejeX g=@(x) (heaviside(x+L)-heaviside(x)).*(L+x)+(heaviside(x)-heaviside(x-L)).*(L-x); fX=@(x) g(x-round(x/(2*L))*2*L); L=1; %función periódica 2L por el eje Y g=@(x) (heaviside(x+L)-heaviside(x)).*(L+x)+(heaviside(x)-heaviside(x-L)).*(L-x); subplot(1,3,1) delta=0; %desfase fY=@(x) g(x+delta-round((x+delta)/(2*L))*2*L); fplot(fX, fY, [-m,m]) axis square subplot(1,3,2) delta=L/4; fY=@(x) g(x+delta-round((x+delta)/(2*L))*2*L); fplot(fX, fY, [-m,m]) axis square subplot(1,3,3) delta=L/2; fY=@(x) g(x+delta-round((x+delta)/(2*L))*2*L); fplot(fX, fY, [-m,m]) axis square
Referencias
J. Flemming, A. Hornes. Lissajous-like figures with triangular and square waves. Revista Brasileira de Ensino de Física, v. 35, n. 3, 3702 (2013). https://www.scielo.br/j/rbef/i/2013.v35n3/
Deyvid W da M Pastana, Manuel E Rodrigues. Using Mathematica software to graph Lissajous figures. Eur. J. Phys. 42 (2021) 065802

