La función symsum(f,a,b) suma la expresión f a medida que la variable simbólica varía de a a b.

${\displaystyle s={\displaystyle \sum _{k=1}^5{k}^2}=1^2+2^2+3^2+4^2+5^2=55}$

>> symsum(k^2,1,5)
ans =55

${\displaystyle {\displaystyle \sum _{k=0}^{N}k=\frac{N(N+1)}{2}}{\displaystyle \sum _{k=0}^N{k}^2=\frac{N(N+1)(2N+1)}{6}}}$

>> syms k N;
>> symsum(k,0,N)
ans =(N*(N + 1))/2
>> symsum(k^2,0,N)
ans =(N*(2*N + 1)*(N + 1))/6

Dado que hay dos variables simbólicas x y k, especificamos en el segundo parámetro de la función sysmsum que la suma se refiere a k

Probar los siguientes resultados

${\displaystyle \begin{array}{l}{\displaystyle \sum _{k=1}^{\infty }\frac{1}{k^2}=\frac{{\pi }^2}{6}}\\ {\displaystyle \sum _{k=0}^{\infty }k(k+1)=\frac{N(N+1)(N+2)}{3}}\\ {\displaystyle \sum _{k=0}^{\infty }\frac{{(-1)}^k}{2k+1}=\frac{\pi }{4}}\end{array}}$

Progresión aritmética

Una progresión aritmética se define como aquella sucesión en la que el término n es la suma del término n-1 más un número r denominado razón de la progresión.

a₀=a
a₁=a+r
a₂=a+2r
a₃=a+3r
………..
a_n=a+n·r

Suma de n términos de una progresión aritmética

S_n=a₀+(a₀+r)+ (a₀+2r)+(a₀+3r)+…(a₀+(n-1)·r)+(a₀+n·r)
S_n=(a_n-n·r)+(a_n-(n-1)·r)+…+(a_n-3r)+(a_n-2r)+(a_n-r)+a_n

Sumando las dos formas de expresar la suma de n términos de una progresión aritmética, 2S_n=(n+1)(a₀+a_n)

${\displaystyle S_n=\frac{n+1}{2}(a_0+a_n)=(n+1)\left(a_0+\frac{1}{2}nr\right)}$

>> syms a k r n;
>> symsum((a+k*r),k,0,n)
ans =a*(n + 1) + (n*r*(n + 1))/2 

Suma de la progresión aritmética, 2+(2+1·3)+(2+2·3)+(2+3·3)+(2+4·3)=2+5+8+11+14

${\displaystyle S_4=(4+1)\left(2+\frac{1}{2}4·3\right)=40}$

>> symsum((2+k*3),k,0,4)
ans =40

Progresión geométrica

Una progresión geométrica se define como aquella sucesión en la que el término n es el producto del término n-1 por un número r denominado razón de la progresión.

a₀=a
a₁=a·r
a₂=a·r²
a₃=a·r³
………..
a_n=a·rⁿ

Suma de n términos de una progresión geométrica

S_n=a₀+a₀·r+ a₀·r²+…+a₀·rⁿ
S_n+1=a₀+a₀·r+ a₀·r²+… +a₀·rⁿ+a₀·rⁿ⁺¹

Multiplicamos la primera igualdad por r y restamos miembro a miembro la segunda menos la primera

S_n+1-r·S_n = a₀

Teniendo en cuenta que  S_n+1=S_n+a₀·rⁿ⁺¹, despejamos la suma S_n de n términos de la progresión geométrica

${\displaystyle S_n=a_0\frac{1-r^{n+1}}{1-r}}$

>> syms r k;
>> syms n integer positive;
>> symsum(r^k,k,0,n)
>> piecewise([r == 1, n + 1], [r ~= 1, (r^(n + 1) - 1)/(r - 1)])

Vamos a sumar, 2+2·5+2·5²+2·5³=2+10+50+250=312

>> symsum(2*5^k,k,0,3)
ans =312

Aplicando la fórmula de la suma de una progresión geométrica

${\displaystyle S_3=2\frac{1-5^4}{1-5}=312}$

Calcular la suma de los términos de la progresión 1/2+1/4+1/8+1/16

${\displaystyle S_3=\frac{1}{2}\frac{1-{\left(\frac{1}{2}\right)}^4}{1-\frac{1}{2}}=\frac{15}{16}}$

>> symsum((1/2)^k/2,k,0,3)
ans =15/16
>> format rat
>> 1/2+1/4+1/8+1/16
ans =      15/16   

Si r es menor que la unidad, la suma de los infinitos términos de una progresión geométrica se reduce a

${\displaystyle S_{\infty }=\frac{a_0}{1-r}}$

Vamos a calcular la suma de los infinitos términos de la progresión 1/2+1/4+1/8+1/16+....

>> symsum((1/2)^k/2,k,0,inf)
ans =1

${\displaystyle S_{\infty }=\frac{1}{2}\frac{\frac{1}{2}}{1-\frac{1}{2}}=1}$

La suma de los infinitos términos de la progresión 1/2-1/4+1/8-1/16+....

>>  symsum((-1/2)^k/2,k,0,inf)
ans =1/3

${\displaystyle S_{\infty }=\frac{1}{2}\frac{\frac{1}{2}}{1-\left(-\frac{1}{2}\right)}=\frac{1}{3}}$

Producto de series

El factorial n!=1·2·3·....n

>> symprod(n)
ans =factorial(n)

Queremos multiplicar 1·3·5·....(2n-1)

>> res=symprod(2*n-1)
res =(1/2^(2*n)*2^(n + 1)*factorial(2*n))/(2*factorial(n))
>> simplify(res)
ans =factorial(2*n)/(2^n*factorial(n))

El resultado es

${\displaystyle 1·3·5·7·\mathrm{...}(2n-1)=\frac{(2n)!}{2^{n}n!}}$

Desarrollo en serie de Taylor

La fórmula general del desarrollo en serie de la función f(x) alrededor de x=a es

${\displaystyle {\displaystyle \sum _{k=0}^{\infty }\frac{f^{\text{'}k}(a)}{k!}{(x-a)}^k}}$

donde el numerador es la derivada k-ésima de f(x) evaluada en x=a.

taylor(f,n+1,a), proporciona los primeros términos del desarrollo en serie de Taylor de la función f alrededor del punto x=a. Si se omite a se toma x=0, por defecto

• ${\displaystyle \frac{1}{1-x}=1+x+x^2+x^3+\mathrm{...}={\displaystyle \sum _{n=0}^{\infty }{x}^n}}$

>> syms x;
>> taylor(1/(1-x))
ans =x^5 + x^4 + x^3 + x^2 + x + 1

Comprobamos el término general,

>>  syms x n;
>> symsum(x^n,n,0,inf)
 ans =-1/(x - 1)

• ${\displaystyle \frac{1}{1+x}=1-x+x^2-x^3+\mathrm{...}={\displaystyle \sum _{n=0}^{\infty }{(-x)}^n}}$

>> syms x;
>> taylor(1/(1+x))
 ans =- x^5 + x^4 - x^3 + x^2 - x + 1

Comprobamos el término general,

>>  syms x n;
>> symsum((-x)^n,n,0,inf)
ans =1/(x + 1)

• ${\displaystyle \ln (1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\mathrm{...}={\displaystyle \sum _{n=0}^{\infty }{(-1)}^{n+1}\frac{x^n}{n}}}$

>> syms x;
>> taylor(log(1+x))
ans = x^5/5 - x^4/4 + x^3/3 - x^2/2 + x
>> taylor(log(x),x,1,'order',7)
ans =x - (x - 1)^2/2 + (x - 1)^3/3 - (x - 1)^4/4 + (x - 1)^5/5 - 1

Comprobamos el término general, x no puede ser -1, y el valor absoluto de x tiene que ser menor que 1

>> syms x n;
>> assume (x ~= -1 & abs(x) <= 1)
>> symsum((-1)^(n+1)*x^n/n,n,1,inf)
ans =log(x + 1)

• ${\displaystyle e^x=1+x+\frac{x^2}{2}+\frac{x^3}{3!}+\frac{x^4}{4!}+\mathrm{...}={\displaystyle \sum _{n=0}^{\infty }\frac{x^n}{n!}}}$

>> syms x;
>> taylor(exp(x))
ans =x^5/120 + x^4/24 + x^3/6 + x^2/2 + x + 1

Comprobamos el término general,

>> syms x n;
>> symsum(x^n/sym('n!'),n,0,inf)
ans =exp(x)

Aproximamos la función exponencial por su desarrollo en serie alrededor del punto x=0

hold on
fplot(@(x) exp(x),[-2,2],'color','k', 'lineWidth',1.5)
line([-2,2],[1,1])
fplot(@(x) 1+x,[-2,2])
fplot(@(x) 1+x+x.^2/2,[-2,2])
fplot(@(x) 1+x+x.^2/2+x.^3/6,[-2,2])
fplot(@(x) 1+x+x.^2/2+x.^3/6+x.^4/24,[-2,2])
hold off
xlabel('x')
ylabel('y')
grid on
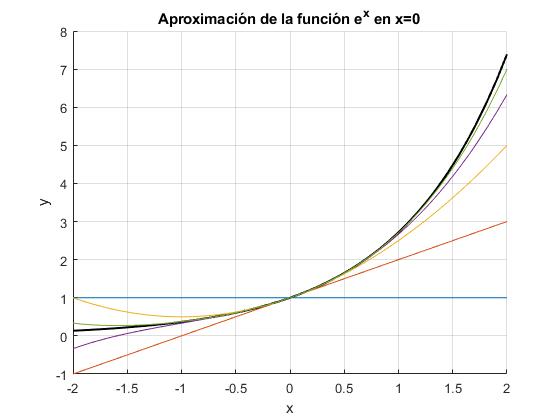
title('Aproximación de la función e^x en x=0')

Como apreciamos en la figura, el polinomio de cuarto grado se aproxima bastante bien a la función exponencial en el intervalo [-2,2]



• ${\displaystyle \sin (x)=x-\frac{1}{3!}{x}^3+\frac{1}{5!}{x}^5-\frac{1}{7!}{x}^7+\mathrm{...}={\displaystyle \sum _{k=0}^{\infty }\frac{{(-1)}^n}{(2n+1)!}}{x}^{2n+1}}$

>> syms x;
>> taylor(sin(x))
ans =x^5/120 - x^3/6 + x

Comprobamos el término general,

>> syms n x;
>> f=(-1)^n*x^(2*n+1)/sym('(2*n+1)!');
>> symsum(f,n,0,inf)
ans =sin(x)

• ${\displaystyle \cos (x)=1-\frac{1}{2!}{x}^2+\frac{1}{4!}{x}^4-\mathrm{...}={\displaystyle \sum }_{k=0}^{\infty }\frac{{(-1)}^n}{(2n)!}{x}^{2n}}$

>> syms x;
>> taylor(cos(x))
ans =x^4/24 - x^2/2 + 1

Comprobamos el término general,

>>  syms x n;
>> f=(-1)^n*x^(2*n)/sym('(2*n)!');
>> symsum(f,n,0,inf) 
ans =cos(x)

• ${\displaystyle \sinh (x)=x+\frac{x^3}{3!}+\frac{x^5}{5!}+\mathrm{...}={\displaystyle \sum }_{k=0}^{\infty }\frac{1}{(2n+1)!}{x}^{2n+1}}$

>> syms x;
>> taylor(sinh(x))
ans =x^5/120 + x^3/6 + x

Comprobamos el término general,

>>  syms x n;
>> symsum(x^(2*n+1)/sym('(2*n+1)!'),n,0,inf)
ans =sinh(x)

• ${\displaystyle \cosh (x)=1+\frac{x^2}{2!}+\frac{x^4}{4!}+\mathrm{...}={\displaystyle \sum }_{k=0}^{\infty }\frac{1}{(2n)!}{x}^{2n}}$

>> syms x;
>> taylor(cosh(x))
ans =x^4/24 + x^2/2 + 1

Comprobamos el término general,

>>  syms x n;
>> symsum(x^(2*n)/sym('(2*n)!'),n,0,inf)
ans =cosh(x)

• ${\displaystyle {\tan }^{-1}(x)=x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\mathrm{...}={\displaystyle \sum }_{k=0}^{\infty }\frac{{(-1)}^n}{2n+1}{x}^{2n+1}}$

>> syms x;
>> taylor(atan(x),'order',10)
 ans =x^9/9 - x^7/7 + x^5/5 - x^3/3 + x

Comprobamos el término general,

>>  syms x n;
>> assume(abs(x)<1)
>> symsum((-1)^n*x^(2*n+1)/(2*n+1),n,0,inf)
ans =atan(x)

Fórmula de Euler

Comprobamos que exp(ix)=cos(x)+i·sin(x)

${\displaystyle \begin{array}{l}{e}^{ix}=1-\frac{1}{2!}{x}^2+\frac{1}{4!}{x}^4-\frac{1}{6!}{x}^6+\mathrm{...}+i\left(x-\frac{1}{3!}{x}^3+\frac{1}{5!}{x}^5-\frac{1}{7!}{x}^7+\mathrm{...}\right)\\ =\cos (x)+i\sin (x)\end{array}}$

>> syms x;
>> assume(x,'real')
>> y=taylor(exp(1i*x),x,0,'Order',6);
>> real(y)
ans =x^4/24 - x^2/2 + 1
>> imag(y)
ans =x^5/120 - x^3/6 + x
>> taylor(cos(x))
ans =x^4/24 - x^2/2 + 1
>> taylor(sin(x))
ans =x^5/120 - x^3/6 + x

Aproximación de una función

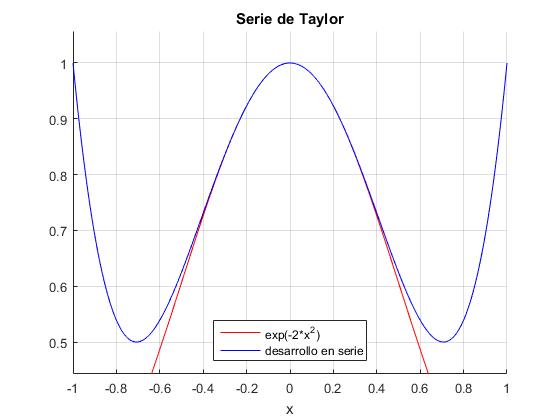
Representamos gráficamente la función exp(-2·x²) en color rojo y los primeros términos de su desarrollo en serie en color azul.

syms x;
y=exp(-2*x^2);
y1=taylor(y) %desarrollo en serie
hold on
g1=ezplot(y,[-1 1]);
set(g1,'color','red')
g2=ezplot(y1,[-1 1]);
set(g2,'color','blue')
legend('exp(-2*x^2)','desarrollo en serie','Location','South')
title('Serie de Taylor')
grid on
hold off

y1 =2*x^4 - 2*x^2 + 1

Ejemplos en el curso de Física

Sucesivos rebotes en el plano horizontal

Sucesivos rebotes en un plano inclinado

Extracción óptima del calor