En la figura, se representa un fluido comprendido entre una lámina inferior fija y una lámina superior móvil.

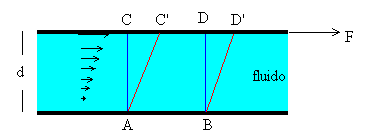
La capa de fluido en contacto con la lámina móvil tiene la misma velocidad que ella, mientras que la adyacente a la pared fija está en reposo. La velocidad de las distintas capas intermedias aumenta uniformemente entre ambas láminas tal como sugieren las flechas. Un flujo de este tipo se denomina laminar.

Como consecuencia de este movimiento, una porción de líquido que en un determinado instante tiene la forma ABCD, al cabo de un cierto tiempo se deformará y se transformará  en la porción ABC’D’.

Sean dos capas de fluido de área S que distan dx y entre las cuales existe una diferencia de velocidad dv.

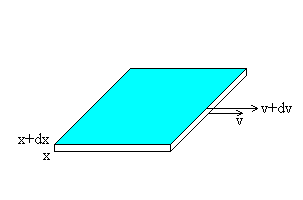
La fuerza por unidad de área que hay que aplicar es proporcional al gradiente de velocidad. La constante de proporcionalidad se denomina viscosidad η.

${\displaystyle \frac{F}{A}=\eta \frac{dv}{dx}}$

En el caso particular, de que la velocidad aumente uniformemente, como se indicó en la primera figura, la expresión se escribe

${\displaystyle \frac{F}{A}=\eta \frac{v}{d}}$

En la figura, se representan dos ejemplos de movimiento de un fluido a lo largo de una tubería horizontal alimentada por un depósito grande que contiene líquido a nivel constante. Cuando el tubo horizontal está cerrado todos los tubos manométricos dispuestos a lo largo de la tubería marcan la misma presión p=p₀+ρgh. Al abrir el tubo de salida los manómetros registran distinta presión según sea el tipo de fluido.

Fluido ideal

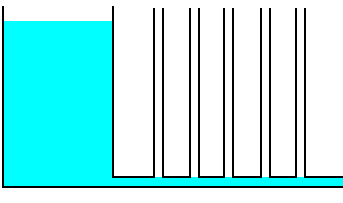
Un fluido ideal (figura de la izquierda) sale por la tubería con una velocidad,$v=\sqrt{2gh}$ , de acuerdo con el teorema de Torricelli. Toda la energía potencial disponible (debido a la altura h) se transforma en energía cinética. Aplicando la ecuación de Bernoulli comprobamos que la altura del líquido en los manómetros debe ser cero.

Fluido viscoso

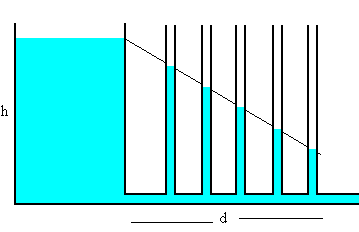
En un fluido viscoso (figura de la derecha) el balance de energía es muy diferente. Al abrir el extremo del tubo, sale fluido con una velocidad bastante más pequeña. Los tubos manométricos marcan alturas decrecientes, informándonos de las pérdidas de energía por rozamiento viscoso. En la salida, una parte de la energía potencial que tiene cualquier elemento de fluido al iniciar el movimiento se ha transformado íntegramente en calor. El hecho de que los manómetros marquen presiones sucesivamente decrecientes nos indica que la pérdida de energía en forma de calor es uniforme a lo largo del tubo

Viscosidad de algunos líquidos

Ley de Poiseuille

Consideremos ahora un fluido viscoso que circula en régimen laminar por una tubería de radio interior R y de longitud L, bajo la acción de una fuerza debida a la diferencia de presión existente en los extremos del tubo.

F=(p₁-p₂)π r²

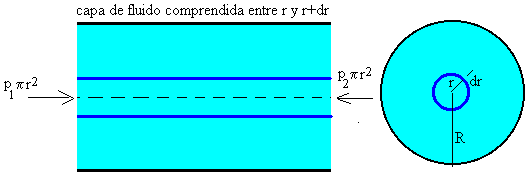
Sustituyendo F en la definición de viscosidad y teniendo en cuenta que el área A de la capa es ahora el área lateral de un cilindro de longitud L y radio r.

${\displaystyle \frac{\left(p_1-p_2\right)\pi r^2}{2\pi rL}=-\eta \frac{dv}{dr}}$

El signo negativo se debe a que v disminuye al aumentar r.

Perfil de velocidades

Integrando esta ecuación, obtenemos el perfil de velocidades en función de la distancia radial, al eje del tubo. Se ha de tener en cuenta que la velocidad en las paredes del tubo r=R es nula.

${\displaystyle -{\displaystyle \underset{v}{\overset{0}{\int }}dv}=\frac{p_1-p_2}{2\eta L}{\displaystyle \underset{r}{\overset{R}{\int }}rdrv=}\frac{p_1-p_2}{4\eta L}\left(R^2-r^2\right)}$

que es la ecuación de una parábola.

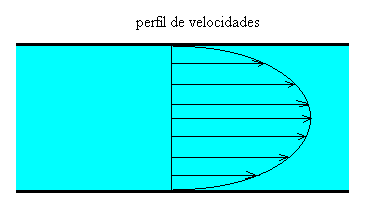
El flujo tiene por tanto un perfil de velocidades parabólico, siendo la velocidad máxima en el centro del tubo.

Gasto

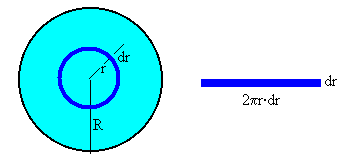
El volumen de fluido que atraviesa cualquier sección normal del tubo en la unidad de tiempo se denomina gasto.

El volumen de fluido que atraviesa el área del anillo comprendido entre r y r+dr en la unidad de tiempo es v(2π rdr). Donde v es la velocidad del fluido a una distancia r del eje del tubo y 2π rdr es el área del anillo

El gasto se hallará integrando

${\displaystyle G={\displaystyle \underset{0}{\overset{R}{\int }}v2\pi rdr}=\frac{\pi \left(p_1-p_2\right)}{2\eta L}{\displaystyle \underset{0}{\overset{R}{\int }}\left(R^2-r^2\right)rdr}=\frac{\pi }{8}\frac{\left(p_1-p_2\right)R^4}{\eta L}}$

El gasto G es inversamente proporcional a la viscosidad η y varía en proporción directa a la cuarta potencia del radio del tubo R, es directamente proporcional al gradiente de presión a lo largo del tubo, es decir, al cociente (p₁-p₂)/L.

El gasto se puede expresar G=πR²<v>, donde <v> es la velocidad media del fluido

${\displaystyle p_1-p_2=\frac{8\eta L}{R^2}<v>}$

Actividades

Se introduce

• la viscosidad 1, 2 ó 3, en el control titulado Viscosidad
• el gradiente de presión 1, 2, ó 3, en el control titulado Gradiente de presión

Se pulsa el botón titulado Nuevo

Se muestra el movimiento de partículas de fluido situadas a distintas distancias del eje del tubo. Se comprueba que las velocidades de las partículas son directamente proporcionales al gradiente de presión (p₁-p₂)/L e inversamente proporcionales a la viscosidad η.

Referencias

Francis W. Sears, Mark W. Zemansky. Física. Edt. Aguilar, (1966), pp. 307-313