En la página anterior, se han ajustado datos a funciones no lineales (función potencial y función exponencial) pero que se pueden transformar en funciones lineales. En esta página, vamos a estudiar algunos ejemplos de ajuste a funciones no lineales

Función y=a/x+bx

La función

${\displaystyle y=\frac{a}{x}+bx}$

aparece en el estudio del péndulo compuesto, con y=P²/(4·π²) y x es la distancia entre el centro de masas c.m. y el centro de oscilación O. P es el periodo de oscilación del péndulo compuesto cuando su amplitud es pequeña.

Dada una tabla de valores x_j e y_j se trata de calcular los valores de los coeficientes a y de b que mejor ajustan a los datos experimentales. El procedimiento aplicado es similar a la regresión lineal

Si (x_j, y_j) son las coordenadas de un dato experimental, a la abscisa x_j le correspondería la ordenada y=a/x_j+bx_j. La diferencia es

${\displaystyle d_j=y_j-\frac{a}{x_j}-b{x}_j}$

Calcularemos los valores de los parámetros a y b que hacen que la suma

${\displaystyle S(a,b)={\displaystyle \sum _1^m{d}_j^2}={\displaystyle \sum _1^m{\left(y_j-\frac{a}{x_j}-b{x}_j\right)}^2}}$

sea mínima.

${\displaystyle \begin{array}{l}\frac{\partial S}{\partial a}=0{\displaystyle \sum _1^{m}2\left(y_j-\frac{a}{x_j}-b{x}_j\right)}\left(-\frac{1}{x_j}\right)=0\\ \left({\displaystyle \sum _1^m\frac{1}{x_j^2}}\right)a+mb={\displaystyle \sum _1^m\frac{y_j}{x_j}}\\ \frac{\partial S}{\partial b}=0{\displaystyle \sum _1^{m}2\left(y_j-\frac{a}{x_j}-b{x}_j\right)}\left(-x_j\right)=0\\ ma+\left({\displaystyle \sum _1^m{x}_j^2}\right)b={\displaystyle \sum _1^m{x}_j{y}_j}\end{array}}$

Resolvemos el sistema de dos ecuaciones con dos incógnitas, para determinar los coeficientes a y b.

${\displaystyle \begin{array}{l}b=\frac{m\left({\displaystyle \sum _1^m\frac{y_j}{x_j}}\right)-\left({\displaystyle \sum _1^m\frac{1}{x_j^2}}\right)\left({\displaystyle \sum _1^m{x}_j{y}_j}\right)}{m^2-\left({\displaystyle \sum _1^m{x}_j^2}\right)\left({\displaystyle \sum _0^{N-1}\frac{1}{x_j^2}}\right)}\\ a=\frac{\left({\displaystyle \sum _1^m{x}_j{y}_j}\right)-\left({\displaystyle \sum _1^m{x}_j^2}\right)b}{m}\end{array}}$

Medimos el periodo P_i de péndulo para cada posición x_i, completando una tabla con N pares de datos

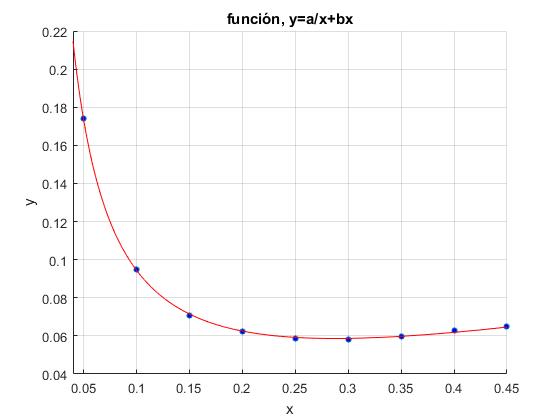
Creamos un script con MATLAB para calcular los valores de a y b. Representamos los datos experimentales y la función que mejor ajusta

x=(5:5:45)/100;  
y=[2.620, 1.936, 1.668, 1.568, 1.520, 1.512, 1.536, 1.576, 1.600].^2/(4*pi^2);
m=length(x);
b=(m*sum(y./x)-sum(1./x.^2)*sum(x.*y))/(m^2-sum(x.^2)*sum(1./x.^2));
a=(sum(x.*y)-b*sum(x.^2))/m;
hold on
%representa los datos experimentales
plot(x,y,'bo','markersize',4,'markerfacecolor','b')
% función
f_ajuste=@(x) a./x+b*x;          
fplot(f_ajuste,[0.04,0.45],'r')
title('función, y=a/x+bx')
xlabel('x')
ylabel('y')
grid on
hold off 

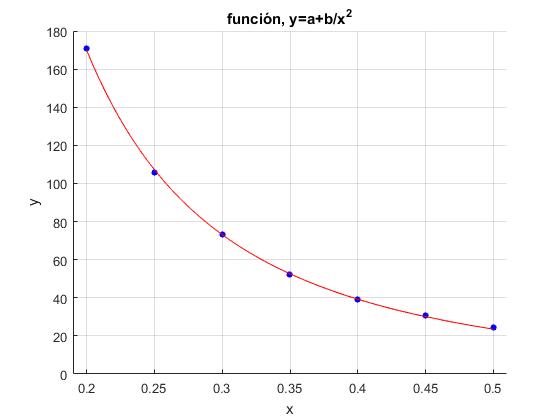
Función, y=a+b/x²

En una experiencia de laboratorio, colocamos un sensor, a una distancia x de la fuente de luz, que vamos cambiando. Obtenemos la siguiente tabla:

Otros ejemplos de este ajuste de datos es la dependencia del índice de refracción de un vidrio con la longitud de onda, o del agua de una gota.

Queremos ajustar m pares de datos (x_i,y_i) a la función

${\displaystyle y=a+\frac{b}{x^2}}$

de modo que la suma S sea mínima

${\displaystyle \begin{array}{l}S={{\displaystyle \sum _{j=1}^m\left(a+\frac{b}{x_j^2}-y_j\right)}}^2\\ \frac{1}{2}\frac{\partial S}{\partial a}=am+b{\displaystyle \sum _{j=1}^m\frac{1}{x_j^2}-{\displaystyle \sum _{j=1}^m{y}_j}}=0\\ \frac{1}{2}\frac{\partial S}{\partial b}=a{\displaystyle \sum _{j=1}^m\frac{1}{x_j^2}}+b{\displaystyle \sum _{j=1}^m\frac{1}{x_j^4}-{\displaystyle \sum _{j=1}^m\frac{y_j}{x_j^2}}}=0\\ \left(\begin{array}{cc}m& {\displaystyle \sum _{j=1}^m\frac{1}{x_j^2}}\\ {\displaystyle \sum _{j=1}^m\frac{1}{x_j^2}}& {\displaystyle \sum _{j=1}^m\frac{1}{x_j^4}}\end{array}\right)\left(\begin{array}{c}a\\ b\end{array}\right)=\left(\begin{array}{c}{\displaystyle \sum _{j=1}^m{y}_j}\\ {\displaystyle \sum _{j=1}^m\frac{y_j}{x_j^2}}\end{array}\right)\end{array}}$

Resolvemos el sistema de dos ecuaciones con dos incógnitas. Creamos la matriz A de los coeficientes y el vector B de los términos independientes, despejamos el vector X de las incógnitas utilizando el operador división por la izquierda \. El elemento X(1) es a y el elemento X(2) del vector X es b.

x=0.2:0.05:0.5;
y=[171,106,73,52,39,30.5,24.5];
A=[length(x),sum(1./x.^2); sum(1./x.^2),sum(1./x.^4)];
B=[sum(y);sum(y./x.^2)];
X=A\B;  % X(1) es a y X(2) es b
hold on
plot(x,y,'bo','markersize',4,'markerfacecolor','b')
f_ajuste=@(x) X(1)+X(2)./x.^2;
fplot(f_ajuste,[x(1),x(end)],'r')
axis([0.19,0.51, 0,180])
grid on
xlabel('x')
ylabel('y')
title('función, y=a+b/x^2')

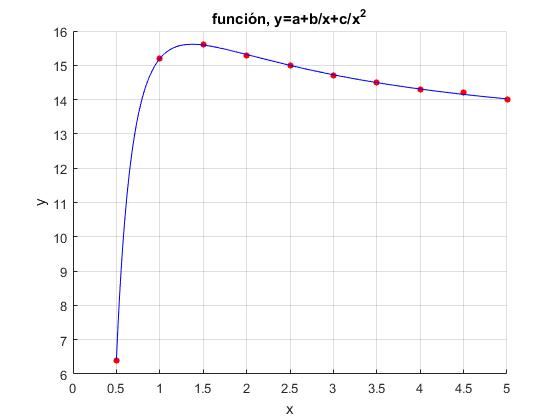
Función, y=a+b/x+c/x²

Queremos ajustar los siguientes pares de datos

a la función

${\displaystyle y=a+\frac{b}{x}+\frac{c}{x^2}}$

de modo que la suma S sea mínima

${\displaystyle \begin{array}{l}S={{\displaystyle \sum _{j=1}^m\left(a+\frac{b}{x_j}+\frac{c}{x_j^2}-y_j\right)}}^2\\ \frac{1}{2}\frac{\partial S}{\partial a}=am+b{\displaystyle \sum _{j=1}^m\frac{1}{x_j}}+c{\displaystyle \sum _{j=1}^m\frac{1}{x_j^2}}-{\displaystyle \sum _{j=1}^m{y}_j}=0\\ \frac{1}{2}\frac{\partial S}{\partial b}=a{\displaystyle \sum _{j=1}^m\frac{1}{x_j}}+b{\displaystyle \sum _{j=1}^m\frac{1}{x_j^2}+c{\displaystyle \sum _{j=1}^m\frac{1}{x_j^3}}}-{\displaystyle \sum _{j=1}^m\frac{y_j}{x_j}}=0\\ \frac{1}{2}\frac{\partial S}{\partial c}=a{\displaystyle \sum _{j=1}^m\frac{1}{x_j^2}}+b{\displaystyle \sum _{j=1}^m\frac{1}{x_j^3}+c{\displaystyle \sum _{j=1}^m\frac{1}{x_j^4}}}-{\displaystyle \sum _{j=1}^m\frac{y_j}{x_j^2}}=0\\ \left(\begin{array}{ccc}m& {\displaystyle \sum _{j=1}^m\frac{1}{x_j}}& {\displaystyle \sum _{j=1}^m\frac{1}{x_j^2}}\\ {\displaystyle \sum _{j=1}^m\frac{1}{x_j}}& {\displaystyle \sum _{j=1}^m\frac{1}{x_j^2}}& {\displaystyle \sum _{j=1}^m\frac{1}{x_j^3}}\\ {\displaystyle \sum _{j=1}^m\frac{1}{x_j^2}}& {\displaystyle \sum _{j=1}^m\frac{1}{x_j^3}}& {\displaystyle \sum _{j=1}^m\frac{1}{x_j^4}}\end{array}\right)\left(\begin{array}{c}a\\ b\\ c\end{array}\right)=\left(\begin{array}{c}{\displaystyle \sum _{j=1}^m{y}_j}\\ {\displaystyle \sum _{j=1}^m\frac{y_j}{x_j}}\\ {\displaystyle \sum _{j=1}^m\frac{y_j}{x_j^2}}\end{array}\right)\end{array}}$

x=0.5:0.5:5;
y=[6.4,15.2,15.6,15.3,15.0,14.7, 14.5,14.3, 14.2,14.0];
A=[length(x),sum(1./x), sum(1./x.^2); sum(1./x),sum(1./x.^2), sum(1./x.^3);
sum(1./x.^2),sum(1./x.^3), sum(1./x.^4)];
B=[sum(y);sum(y./x);sum(y./x.^2)];
X=A\B;  % X(1) es a, X(2) es b y X(3) es c
hold on
plot(x,y,'ro','markersize',4,'markerfacecolor','r')
f_ajuste=@(x) X(1)+X(2)./x+X(3)./x.^2;
fplot(f_ajuste,[x(1),x(end)],'b')
axis([0,5, 6,16])

grid on
xlabel('x')
ylabel('y')
title('función, y=a+b/x+c/x^2')

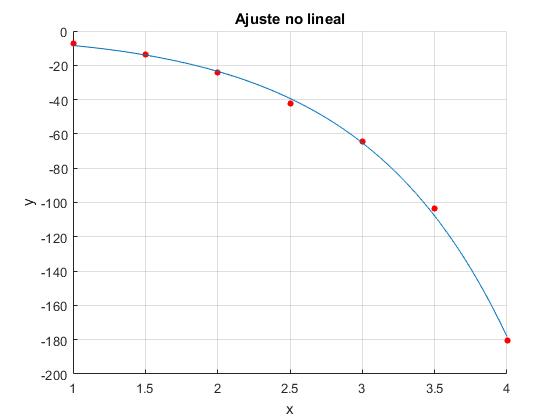
Función y=a·lnx+b·cosx+c·e^x

Supongamos que queremos ajustar los datos (x_j,y_j), j=1,2,...m

a la función y=a·lnx+b·cosx+c·e^x de modo que la suma S sea mínima

${\displaystyle \begin{array}{l}S={{\displaystyle \sum _{j=1}^m\left(a\ln x_j+b\cos x_j+c{e}^{x_j}-y_j\right)}}^2\\ \frac{1}{2}\frac{\partial S}{\partial a}=0\Rightarrow a{\displaystyle \sum _{j=1}^m{\left(\ln x_j\right)}^2}+b{\displaystyle \sum _{j=1}^m\ln x_j\cos x_j}+c{\displaystyle \sum _{j=1}^m\ln x_j{e}^{x_j}}={\displaystyle \sum _{j=1}^m{y}_j\ln x_j}\\ \frac{1}{2}\frac{\partial S}{\partial b}=0\Rightarrow a{\displaystyle \sum _{j=1}^m\cos x_j\ln x_j}+b{\displaystyle \sum _{j=1}^m{\left(\cos x_j\right)}^2}+c{\displaystyle \sum _{j=1}^m\cos x_j{e}^{x_j}}={\displaystyle \sum _{j=1}^m{y}_j\cos x_j}\\ \frac{1}{2}\frac{\partial S}{\partial c}=0\Rightarrow a{\displaystyle \sum _{j=1}^m{e}^{x_j}\ln x_j}+b{\displaystyle \sum _{j=1}^m{e}^{x_j}\cos x_j}+c{\displaystyle \sum _{j=1}^m{\left(e^{x_j}\right)}^2}={\displaystyle \sum _{j=1}^m{y}_j{e}^{x_j}}\end{array}}$

Escribimos el sistema de tres ecuaciones con tres incógnitas de forma matricial

${\displaystyle \begin{array}{l}\left(\begin{array}{cccc}\ln x_1& \ln x_2& \mathrm{...}& \ln x_m\\ \cos x_1& \cos x_2& \mathrm{...}& \cos x_m\\ e^{x_1}& e^{x_2}& \mathrm{...}& e^{x_m}\end{array}\right)\left(\begin{array}{ccc}\ln x_1& \cos x_1& e^{x_1}\\ \ln x_2& \cos x_2& e^{x_2}\\ \mathrm{...}& \mathrm{...}& \mathrm{...}\\ \ln x_m& \cos x_m& e^{x_m}\end{array}\right)\left(\begin{array}{c}a\\ b\\ c\end{array}\right)=\\ \left(\begin{array}{cccc}\ln x_1& \ln x_2& \mathrm{...}& \ln x_m\\ \cos x_1& \cos x_2& \mathrm{...}& \cos x_m\\ e^{x_1}& e^{x_2}& \mathrm{...}& e^{x_m}\end{array}\right)\left(\begin{array}{c}{y}_1\\ y_2\\ \mathrm{...}\\ y_m\end{array}\right)\end{array}}$

Con las funciones a ajustar ln(x), cos(x) y exp(x) y el vector x de las abscisas de los pares de datos, creamos la matriz V. Despejamos el vector columna a de las incógnitas (a,b,c) utilizando el operador división por la izquierda \ en la relación (V^T·V)a=V^T·Y. Siendo Y el vector columna de las ordenadas

x=1:0.5:4;
y=[-7.3,-13.9,-24.2,-42.1,-64.7,-103.5,-180.3];
V=zeros(length(x),3);
V(:,1)=log(x);
V(:,2)=cos(x);
V(:,3)=exp(x);
a=(V'*V)\(V'*y');
hold on
plot(x,y,'ro','markersize',4,'markerfacecolor','r')
z=@(x) a(1)*log(x)+a(2)*cos(x)+a(3)*exp(x);
fplot(z,[x(1),x(end)])
xlabel('x')
ylabel('y')
grid on
title('Ajuste no lineal')
hold off

Ilustramos este procedimiento con un ejemplo más. Ajustamos los datos (x_j, y_j) j=1,2...m de la tabla a la función y=a+b·cos(2πt)+c·sin(2πt)+d·cos(4πt)

Creamos la matriz V

${\displaystyle V=\left(\begin{array}{cccc}1& \cos \left(2\pi x_1\right)& \sin \left(2\pi x_1\right)& \cos \left(4\pi x_1\right)\\ 1& \cos \left(2\pi x_2\right)& \sin \left(2\pi x_2\right)& \cos \left(4\pi x_2\right)\\ \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}\\ 1& \cos \left(2\pi x_m\right)& \sin \left(2\pi x_m\right)& \cos \left(4\pi x_m\right)\end{array}\right)}$

Despejamos el vector a columna de las incógnitas utilizando el operador \

x=0:0.125:0.875;
y=[2.2,2.8,6.1,3.9,0,-1.1,0.6,1.1];
V=zeros(length(x),4);
V(:,1)=1;
V(:,2)=cos(2*pi*x);
V(:,3)=sin(2*pi*x);
V(:,4)=cos(4*pi*x);
a=(V'*V)\(V'*y');
hold on
plot(x,y,'ro','markersize',4,'markerfacecolor','r')
z=@(x) a(1)+a(2)*cos(2*pi*x)+a(3)*sin(2*pi*x)+a(4)*cos(4*pi*x);
fplot(z,[x(1),x(end)])
xlabel('x')
ylabel('y')
grid on
title('Ajuste no lineal')
hold off

>> (V'*V)
ans =
    8.0000   -0.0000   -0.0000   -0.0000
   -0.0000    4.0000    0.0000   -0.0000
   -0.0000    0.0000    4.0000    0.0000
   -0.0000   -0.0000    0.0000    4.0000
>> a
a =
    1.9500
    0.7445
    2.5594
   -1.1250

En la siguiente página, estudiaremos cómo se ajustan los datos a funciones armónicas, cuando las abscisas x_j están igualmente espaciadas, lo que nos permitirá prescindir de la matriz V calculando las incógnitas a,b,c,d de una forma más sencilla ya que como podemos observar la matriz V'*V es diagonal

Ajuste mediante nlinfit o fminsearch

La función nlinfit no está disponible en el paquete estándar de MATLAB, por lo que puede utilizarse alternativamente, fminsearch, tal como se muestra en los ejemplos que siguen

Sea y=f(x) el modelo de función dependiente de uno o más parámetros a(1), a(2),..., a la que queremos ajustar los datos. Definimos la función error

${\displaystyle E_r={\displaystyle \sum _{i=1}^n{\left(y_i-f(x_i)\right)}^2}}$

Donde (x_i, y_i) son los pares de datos y n el número de datos. fminsearch, calcula el valor de los parámetros a(i) de la función y=f(x), que hacen que la función error E_r sea mínima

Ejemplo 1

En un experimento hemos obtenido los siguientes datos:

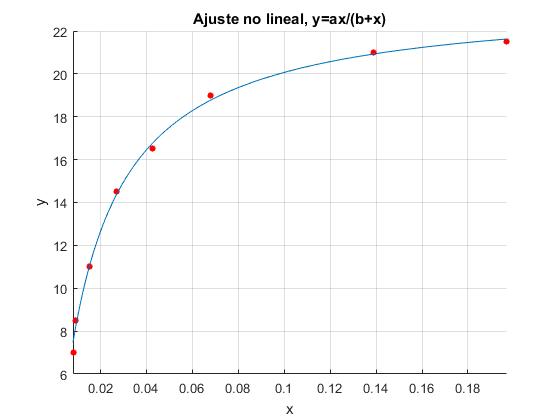
calculamos los parámetros a y b a partir del ajuste de datos por el procedimiento de mínimos cuadrados implementado en la función MATLAB nlinfit, tomando como modelo la función

${\displaystyle y=\frac{ax}{b+x}}$

x=[0.008,0.009,0.015,0.027,0.0427,0.068,0.139,0.197];
y=[7,8.5,11,14.5,16.5,19,21,21.5];
hold on
plot(x,y,'ro','markersize',4,'markerfacecolor','r')
f=@(a,x) a(1)*x./(a(2)+x);      
a0=[23,0.02];  %valor inicial
af=nlinfit(x,y,f,a0)
g=@(x) f(af,x);
fplot(g,[x(1),x(end)])
title('Ajuste no lineal, y=ax/(b+x)')
xlabel('x')
ylabel('y')
grid on
hold off 

Corremos el script en la ventana de comandos

af =   23.5104    0.0171

Alternativamente, con fminsearch

x=[0.008,0.009,0.015,0.027,0.0427,0.068,0.139,0.197];
y=[7,8.5,11,14.5,16.5,19,21,21.5];
hold on
plot(x,y,'ro','markersize',4,'markerfacecolor','r')
f=@(a,x) a(1)*x./(a(2)+x);      
error=@(a) sum((y-f(a,x)).^2);
a0=[23,0.02];  %valor inicial
af=fminsearch(error,a0);
g=@(x) f(af,x);
fplot(g,[x(1),x(end)])
title('Ajuste no lineal, y=ax/(b+x)')
xlabel('x')
ylabel('y')
grid on
hold off 

Ejemplo 2

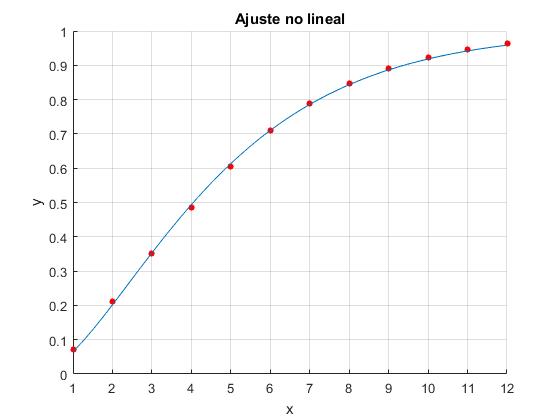
En un experimento hemos obtenido los siguientes datos:

Calculamos los parámetros a y b a partir del ajuste de datos por el procedimiento de mínimos cuadrados implementado en la función MATLAB nlinfit, tomando como modelo la función

${\displaystyle y=1-\frac{a\exp (-x/a)-b\exp (-x/b)}{a-b}}$

x=1:12;
y=[0.07 0.21 0.35 0.485 0.605 0.71 0.79 0.847 0.89 0.924 0.946 0.963];
hold on
plot(x,y,'ro','markersize',4,'markerfacecolor','r')
f=@(a,x) 1-(a(1)*exp(-x/a(1))-a(2)*exp(-x/a(2)))/(a(1)-a(2));      
a0=[2 1];  %valor inicial
af=nlinfit(x,y,f,a0)
g=@(x) f(af,x);
fplot(g,[x(1),x(end)])
title('Ajuste no lineal')
xlabel('x')
ylabel('y')
grid on
hold off 

Corremos el script en la ventana de comandos

af =    2.4120    2.4119

Alternativamente, con fminsearch

x=1:12;
y=[0.07 0.21 0.35 0.485 0.605 0.71 0.79 0.847 0.89 0.924 0.946 0.963];
hold on
plot(x,y,'ro','markersize',4,'markerfacecolor','r')
f=@(a,x) 1-(a(1)*exp(-x/a(1))-a(2)*exp(-x/a(2)))/(a(1)-a(2));      
error=@(a) sum((y-f(a,x)).^2);
a0=[2 1];  %valor inicial
af=fminsearch(error,a0);
g=@(x) f(af,x);
fplot(g,[x(1),x(end)])
title('Ajuste no lineal')
xlabel('x')
ylabel('y')
grid on
hold off 

Ejemplo 3

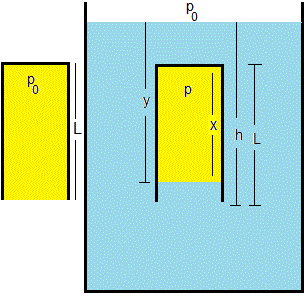
Consideremos un tubo de longitud L y sección S abierto por la parte inferior y cerrado por la parte superior. Lo introducimos en un fluido de densidad ρ conocida. A medida que sumergimos el tubo, el aire atrapado en su interior (en color amarillo) se comprime.

Sea p₀=101 300 N/m² la presión atmósférica. Sea h la posición del extremo inferior del tubo e y la posición de la superficie de separación entre el fluido y el aire atrapado en el tubo. Ambas longitudes se miden desde la superficie libre del fluido tal como se muestra en la figura

Suponiendo una transformación isotérmica, como se ha explicado al final de la página titulada Aplicaciones de la ecuación fundamental de la estática de fluidos, la relación entre x (altura de la columna de aire) y h (profundidad del tubo) es

${\displaystyle \begin{array}{l}\begin{array}{l}p\left(Sx\right)=p_0\left(SL\right)\\ y=h-\left(L-x\right)\end{array}\hfill \\ p=p_0+\rho gy\hfill \end{array}}$

Despejamos x en función de h

${\displaystyle \begin{array}{l}{x}^2+\left(\frac{p_0}{\rho g}+h-L\right)x-\frac{p_0}{\rho g}L=0\\ x=\frac{-\left(\frac{p_0}{\rho g}+h-L\right)+\sqrt{{\left(\frac{p_0}{\rho g}+h-L\right)}^2+4\frac{p_0}{\rho g}L}}{2}\end{array}}$

Conocida la presión atmosférica p₀=101 300 N/m², la longitud del tubo, L=90 cm y la densidad del fluido agua ρ=1000 kg/m³, procedemos a un ajuste no lineal para obtener la aceleración g de la gravedad. Denominamos al parámetro a=p₀/(ρ·g)

${\displaystyle x=\frac{-\left(a+h-L\right)+\sqrt{{\left(a+h-L\right)}^2+4aL}}{2}}$

El programa interactivo, genera los valores de x (altura de la columna de aire) en cm en función de h (profundidad del tubo), en cm, pulsando el botón titulado Medida

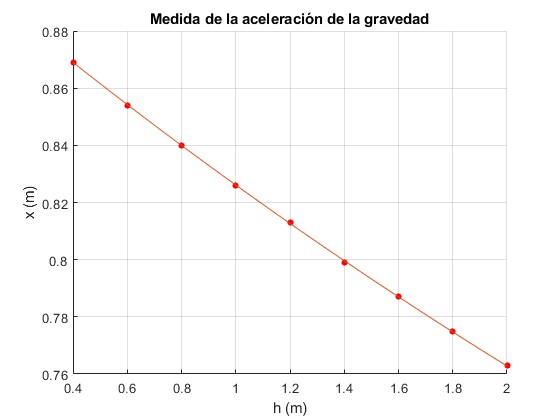
Las medidas tomadas han sido las siguientes:

x=(40:20:200)/100; %profundidad
y=[86.9, 85.4, 84.0, 82.6, 81.3, 79.9, 78.7, 77.5,76.3]/100; %altura aire
L=90/100;  %longitud del tubo
p0=101300; %presión atmosférica
rho=1000; %densidad del agua
hold on
plot(x,y,'ro','markersize',4,'markerfacecolor','r')
f=@(a,x) (-(a-L+x)+sqrt((a-L+x).^2+4*a*L))/2;      
error=@(a) sum((y-f(a,x)).^2);
a0=10;  %valor inicial
af=fminsearch(error,a0);
disp(p0/(af*rho))
g=@(x) f(af,x);
fplot(g,[x(1),x(end)])
hold off 
grid on
xlabel('h (m)')
ylabel('x (m)')
title('Medida de la aceleración de la gravedad')

    9.7813

La aceleración de la gravedad es, g=9.7813 m/s²

Ejemplos en el curso de Física. Ajuste no lineal: nlinfit o fminsearch

La carrera de los 100 m lisos

Modelo PREM del interior de la Tierra

Péndulo compuesto.

El prisma de vidrio

El arco iris

Carga de un condensador

Fuerza magnética sobre conductor rectilíneo. La balanza de corriente

Medida de la difusividad térmica

Datos de las olas del mar

Análisis de las alturas y periodos de las olas

Función de distribución de Weibull

Función de distribución de Rayleigh

Energía producida por un aerogenerador