Fuerza de rozamiento. Coeficiente de arrastre
La fórmula de la fuerza de rozamiento es
Donde CD se denomina coeficiente de arrastre, ρf es la densidad del fluido, A es el área de la sección transversal a la dirección del movimiento (en el caso de una esfera es πD2/4) y v es la velocidad relativa del objeto respecto del fluido.
El coeficiente de arrastre es una función del número de Reynolds, Re. Este número es importante para definir el comportamiento de un fluido y en particular, la transición del flujo laminar al turbulento. El número Re se define para un objeto esférico de diámetro D
η es la viscosidad del fluido.
Existen fórmulas que describen con mayor o menor aproximación las medidas del coeficiente de arrastre CD para un objeto de forma esférica en un amplio intervalo de números de Reynolds, Re.
Esta fórmula describe bien la zona alrededor de Re=2·106 donde el coeficiente de arrastre cambia apreciablemente con el número Re
Otra fórmula válida para Re<106 mucho más simple es
con a=24, b=0.32 y c=0.52
Creamos un script para representar ambas funciones en un diagrama doblemente logarítmico
a=24;
b=0.32;
c=0.52;
c1=@(x) ((a./x).^c+b^c).^(1/c);
c2=@(x) 24./x+2.6*(x/5.0)./(1+(x/5.0).^1.52)+0.411*((x/263000).^-7.94)./
(1+(x/263000).^-8.00)+0.25*(x/1e6)/(1+x/1e6);
re=logspace(-2,6,100);
loglog(re,c2(re), re,c1(re))
grid on
xlabel('Re')
ylabel('C_D')
legend('(1)','(2)')
title('Coeficiente C_D de arrastre')
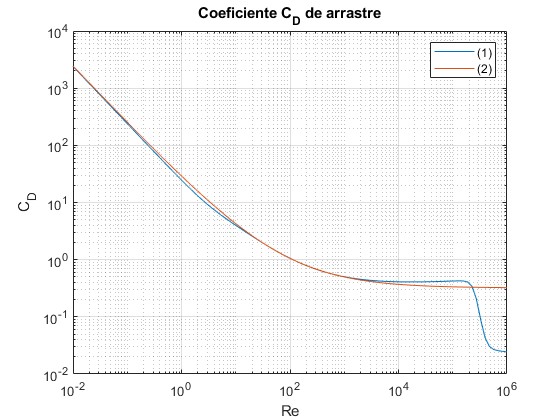
Ambas descripciones coinciden en un amplio intervalo de números de Reynolds, salvo en la zona donde CD cambia rápidamente Re>2·105 (parte derecha de la gráfica). Para números de Reynolds del orden de 104 hasta 2·105 el coeficiente de arrastre se mantiene casi constante próximo a CD=0.4
Fórmula de Stokes
Para una esfera de diámetro D que se mueve en un fluido con bajos números de Reynolds CD=24/Re. La fuerza de rozamiento vale
que es la fórmula de Stokes
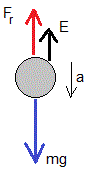
Supongamos que una esfera de masa m se deja caer en el seno de un fluido, al cabo de un cierto tiempo, teóricamente infinito, alcanza una velocidad límite constante v∞. El peso menos el empuje se hace igual a la fuerza de rozamiento, mg-E=Fr, la acelearción a=0
ρs es la densidad del sólido y ρf la del fluido. D es el diámetro de la esfera
El número de Reynolds Re para esta velocidad es
Que crece muy rápidamente con el diámetro D de la esfera. Para
Ejemplo 1: una gota de agua que se deja caer en el aire (se desprecia el empuje)
- densidad del aire, ρf=1.2 kg/m3
- densidad del agua, ρe=1000 kg/m3
- viscosidad del aire, η=18·10-6 Pa·s
Para que Re<1 entonces D<79 μm
Ejemplo 2: una esfera de plomo se deja caer en aceite de automóvil.
- Densidad del plomo, ρs=11 350 kg/m3
- Densidad del aceite, ρf=880 kg/m3
- Viscosidad del aceite, η=0.391 Pa·s
Para que Re<1 entonces D<3 mm
Velocidad límite constante
Supongamos de nuevo, que una esfera de masa m se deja caer en el seno de un fluido, al cabo de un cierto tiempo, teóricamente infinito, alcanza una velocidad límite constante v∞. El peso menos el empuje se hace igual a la fuerza de rozamiento, mg-E=Fr, la aceleración a=0
Donde ρe=ρs-ρf. El coeficiente de arrastre CD depende del número de Reynolds, Re y el número de Reynolds de la velocidad
Utilizamos la función más simple para relacionar el coeficiente de arrastre CD y el número de Reynolds, Re. Un pequeño programa en MATLAB nos permite determinar la velocidad final v∞ para una gota de diámetro D que cae en el aire
a=24;
b=0.32;
c=0.52;
c1=@(x) ((a/x)^c+b^c)^(1/c); %C_D
rho_f=1.2; %densidad del aire
rho_e=1000; %densidad del agua
eta=18e-6; %viscosidad del aire
D=100e-6; %diámetro de la gota de agua
%aproximación inicial, utilizando la fórmula de Stokes
v0=rho_e*9.8*D^2/(18*eta);
while(1)
Re=rho_f*D*v0/eta;
v=2*sqrt(rho_e*9.8*D/(3*c1(Re)*rho_f));
if abs(v-v0)<0.01
break;
end
v0=v;
end
fprintf('La velocidad límite constante de la gota es %1.3f\n',v);
La velocidad límite constante de la gota es 0.242
Que es un poco menor, que la que se obtendría aplicando la fórmula de Stokes v∞=0.302
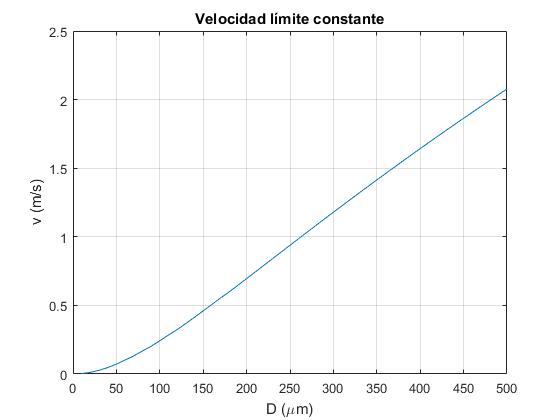
Creamos un script para calcular y representar la velocidad límite constante de gotas de varios diámetros que se dejan caer en el aire.
a=24;
b=0.32;
c=0.52;
c1=@(x) ((a./x).^c+b^c).^(1/c);
rho_f=1.2; %densidad del aire
rho_e=1000; %densidad del agua
eta=18e-6; %viscosidad del aire
D=(10:10:500)*1e-6; %diámetros de la gota de agua
v_inf=zeros(1,length(D));
for i=1:length(D)
v0=rho_e*9.8*D(i)^2/(18*eta);
while(1)
Re=rho_f*D(i)*v0/eta;
v=2*sqrt(rho_e*9.8*D(i)/(3*c1(Re)*rho_f));
if abs(v-v0)<0.01
v_inf(i)=v;
break;
end
v0=v;
end
end
plot(D/1e-6,v_inf)
grid on
xlabel('D (\mum)')
ylabel('v (m/s)')
title('Velocidad límite constante')
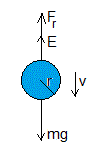
Movimiento de caída de una gota
En la página titulada 'La gota de lluvia que cae a través de una nube' hemos estudiado el movimiento de una gota de lluvia cuya masa se incrementa a medida que cae. En esta caso, la masa de la gota de lluvia permanece constante al moverse en el aire seco.
Sea una gota de lluvia de radio r y masa m quese mueve en aire seco de densidad ρf y viscosidad η. La gota de lluvia experimenta las siguientes fuerzas:
El peso, mg
El empuje del aire
La fuerza de rozamiento
El área de la sección transversal a la dirección del movimiento es algo mayor que πr2, véase la figura al final de la página titulada The shape of a raindrop
Aproximamos el coeficiente de arrastre CD a la siguiente fórmula en el intervalo de números de Reynolds, 0-2·105
c1=@(x) 24*(1+0.15*x.^0.687)./x;
c2=@(x) 24./x+2.6*(x/5.0)./(1+(x/5.0).^1.52)+0.411*((x/263000).^-7.94)./
(1+(x/263000).^-8.00)+0.25*x/1e6/(1+x/1e6);
r1=logspace(-2,3,100);
r2=logspace(3,log10(2e5),50);
loglog(r1,c1(r1),r1,c2(r1), r2, c2(r2), r2, ones(1,length(r2),1)*0.44)
grid on
xlabel('Re')
ylabel('C_D')
legend('(1)','(2)')
title('Coeficiente C_D de arrastre')
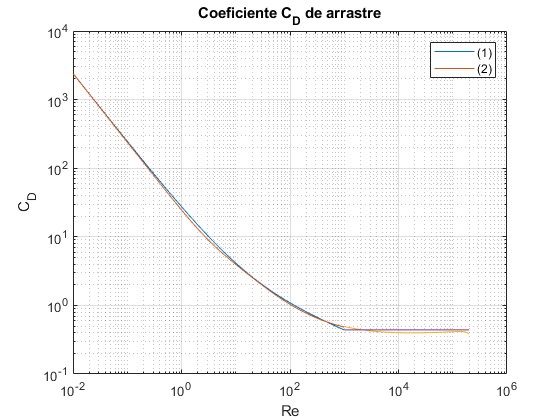
La coincidencia es bastante buena hasta Re=2·105
La fuerza de rozamiento vale
La ecuación del movimiento de la gota es
Suponiendo que el aire es un gas ideal, su densidad ρf es
M=18.9645 g/mol es la masa molecular del aire, la constante R=8.3143 J/(K·mol) de los gases, T=293 es la temperatura (20 °C) en grados kelvin, p=1.013·105 Pa es la presión atmosférica. La viscosidad del aire seco es η=1.82·10-5 Pa·s
Supongamos una gota de agua (ρ=1 g/cm3) de radio r=2.5 mm
La ecuación del movimiento de la gota supuesta, esférica es
Primera etapa del movimiento
Al finalizar la primera etapa
>> integral(@(x) 1./(9.788-0.0131*x-0.1058*x.^1.687),0,3.0222) ans = 0.3178
Segunda etapa
Representamos la velocidad v en función del tiempo t. En la primera etapa, la función es implícita
f=@(t,v) t-integral(@(x) 1./(9.7882-0.0131*x-0.1058*x.^1.687), 0, v);
hold on
fimplicit(f,[0,0.3178,0,3.0222])
v=@(t) tanh((t-0.001)/1.1336)/0.0901;
fplot(v,[0.3178,5])
line([0.3178,0.3178],[0, 3.0222],'lineStyle','--')
line([0,0.3178],[3.0222, 3.0222],'lineStyle','--')
hold off
grid on
xlabel('t')
ylabel('v')
title('Velocidad')
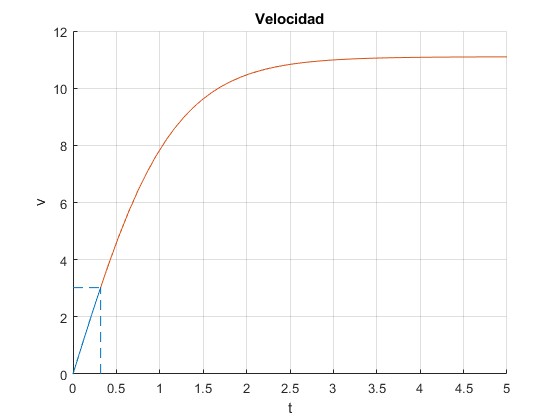
Cuando t se hace grande, tanh tiende hacia 1 y la velocidad límite constante tiende a v∞=1/0.0901=11.0988 m/s
Alternativamente, se obtiene una velocidad límite constante cuando dv/dt=0
Fuerza de rozamiento proporcional a la velocidad y al cuadrado de la velocidad
Para pequeños números Re<1, la expresión de la fuerza de rozamiento sobre un cuerpo de forma esférica de radio R es
Que es la conocida fórmula de Stokes. La fuerza de rozamiento sobre una esfera que se mueve en régimen laminar en un medio es proporcional a la velocidad.
El rango de validez de la fórmula de Stokes (Re<1) limita el radio R de la esfera que empleamos en la experiencia de la medida de la viscosidad de un fluido, para un fluido (aceite) y para un material (plomo) determinado, tal como se ha explicado en el apartado 'Fórmula de Stokes'
Para grandes números Re, el coeficiente de arrastre CD es aproximadamente constante CD≈ 0.4. La fuerza de rozamiento para una esfera de radio R vale
La fuerza de rozamiento es proporcional al cuadrado de la velocidad.
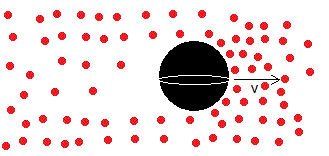
Este modelo de fuerza se justifica cualitativamente del siguiente modo: Un cuerpo de área frontal A=πR2, que se mueve con velocidad v barre un volumen de gas A·vΔt en el tiempo Δt. La masa de gas es ρf·AvΔt, donde ρf es la densidad. Suponiendo que el cuerpo al moverse acelera las partículas del gas hasta la velocidad v del cuerpo. El momento lineal que gana el gas en el tiempo Δt es ρf·Av2Δt. El momento lineal ganado por el gas en la unidad de tiempo es el mismo que pierde el cuerpo en la unidad de tiempo, ρf·Av2 y esta es la fuerza de rozamiento que actúa sobre el cuerpo que se mueve a través del gas
Movimiento horizontal
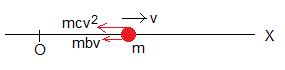
Un ejercicio interesante, consiste en estudiar el movimiento horizontal de una partícula bajo la acción de un fuerza de rozamiento proporcional a la velocidad y de una fuerza de rozamiento proporcional al cuadrado de la velocidad. La ecuación del movimiento es
Integramos esta ecuación, con la condición inicial, en el instante t=0, v=v0
Integramos de nuevo para obtener la posición x del móvil en función del tiempo t, sabiendo que en el instante t=0, parte del origen x=0
Haciendo el cambio de variable u=(b+cv0)ebt
Deshaciendo los cambios, la integral resulta
Cuando t→∞, la partícula se detiene, penetrando una longitud
Expresamos la velocidad v en función de x en vez de t teniendo en cuenta que dv/dt=(dx/dt)(dv/dx)=v(dv/dx). La ecuación del movimiento se escribe
La partícula se detiene v=0, cuando su posición es x=L
Para una esfera de masa m=ρs(4πR3/3), los coeficientes b y c valen
Una esfera de plomo se mueve horizontalmente en aceite de automóvil, suponiendo una velocidad inicial de v0=1 m/s.
- Radio de la esfera, R=1.5 mm
- Densidad del plomo, ρe=11 350 kg/m3
- Densidad del aceite, ρf=880 kg/m3
- Viscosidad del aceite, η=0.391 Pa·s
>> b=9*0.391/(2*11350*0.0015^2) b = 68.8987 >> c=0.2*880/(2*11350*0.0015) c = 5.1689 >> L=log(1+c/b)/c L = 0.0140
La esfera penetra en el aceite una longitud de 1.4 cm
Movimiento vertical

La ecuación del movimiento de una esfera de radio r y densidad ρ que cae en el seno de un fluido de densidad ρf es
Donde ge es la aceleración de la gravedad efectiva
Velocidad de la esfera
El cuerpo parte del reposo, t=0, v=0
Separamos variables e integramos
Expresamos la velocidad en términos del tiempo adimensional t/τ
Definimos u nuevo parámetro k para obtener la velocidad adimensional v/v∞
Casos particulares
Fuerza de rozamiento proporcional al cuadrado de la velocidad, b=0
Fuerza de rozamiento proporcional a la velocidad, c=0
Cuando b=0, k=0
Cuando c=0, τ=2/b, k=∞
Tenemos una indeterminación ∞/∞, que se resuelve aplicando la regla de L'Hôpital
>> syms k a; >> y=(2+2*k)/(1+(1+2*k)*a); >> limit(y,k,inf) ans =1/a
La velocidad límite v∞ es una indeterminación 1/(0·∞) que la convertimos en 0/0
Posición de la esfera
Dada la velocidad v, integramos para obtener la posición x. El cuerpo parte del origen, t=0, x=0
Es una integral del tipo
Hacemos el cambio de variable
Se descompone en dos fracciones
El resultado es
Para tiempos grandes, la exponencial tiende a cero y la ecuación es la de una línea recta de pendiente 1/τ
Casos particulares
Fuerza de rozamiento proporcional al cuadrado de la velocidad, b=0, c≠0
Fuerza de rozamiento proporcional a la velocidad, c=0, b≠0
Cuando b=0, k=0
Cuando c=0, T=2/b, k=∞
Tenemos una indeterminación ∞/∞, que se resuelve aplicando la regla de L'Hôpital
>> syms k a; >> y=(1+k)*log((a+1+2*k)/(2*(1+k))); >> limit(y,k,inf) ans =a/2 - 1/2
Resumen
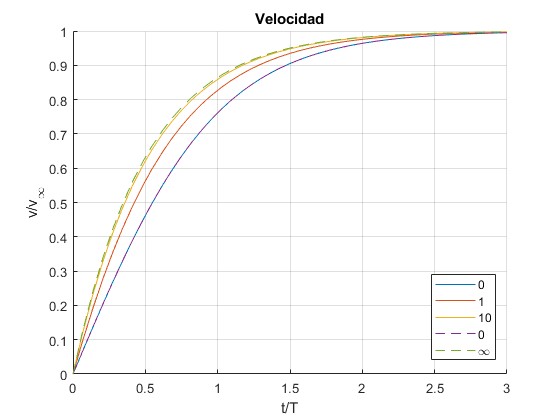
Velocidad
Representamos la velocidad adimensional de la esfera v/v∞ para k=0, 1, 10, utilizando la expresión general
Representamos la velocidad de la esfera (línea a trazos) para los casos particulares k=0 y para k=∞
hold on
for k=[0, 1, 10]
v=@(t) 1-2*(1+k)./(1+(1+2*k)*exp(2*t));
fplot(v,[0,3])
end
fplot(@(t) tanh(t),[0,3], 'lineStyle','--') %k=0
fplot(@(t) 1-exp(-2*t),[0,3], 'lineStyle','--') %k=infinito
hold off
grid on
xlabel('t/T')
ylabel ('v/v_\infty')
legend('0','1','10','0','\infty','location','best')
title('Velocidad')
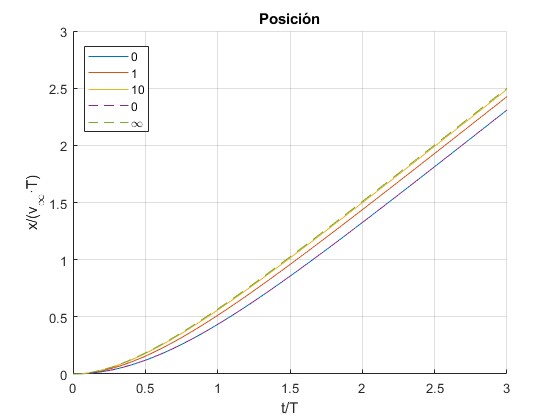
Posición
Representamos la posición adimensional de la esfera x/(v∞τ) para k=0, 1, 10, utilizando la expresión general
Representamos la posición de la esfera (línea a trazos) para los casos particulares k=0 y para k=∞
hold on
for k=[0, 1, 10]
v=@(t) t+(1+k)*log((1+2*k+exp(-2*t))/(2+2*k));
fplot(v,[0,3])
end
fplot(@(t) log(cosh(t)),[0,3], 'lineStyle','--') %k=0
fplot(@(t) t+exp(-2*t)/2-1/2,[0,3], 'lineStyle','--') %k=infinito
hold off
grid on
xlabel('t/T')
ylabel ('x/(v_\infty·T)')
legend('0','1','10','0','\infty','location','best')
title('Posición')
Referencias
Faith A. Morrison, Data Correlation for Drag Coefficient for Sphere, Department of Chemical Engineering, Michigan Technological University, Houghton, MI, 10 November 2016
H.J. Holterman. Kinetics and evaporation of water drops in air. IMAG report 2003-12, Wageningen UR, July 2003
Wayne M Saslow, Hong Lu. Newton on objects moving in a fluid-the penetration length. Eur. J. Phys. 29 (2008) pp. 689-696
SHAO Yun, A study on the free falling motion of raindrops with a diameter of 5 mm in still air at 20 °C. College Physics. 2024, 43 (04)
Aldo Mayme, Carl E Mungan. Vertical fall of a sphere opposed by fluid buoyancy and drag. Eur. J. Phys.46 (2025) 035004
Este artículo está disponible en la dirección: https://www.usna.edu/Users/physics/mungan/Publications/Publications.php#fndtn-panel120162017
Pirooz Mohazzabi. Falling and rising in a fluid with both linear and quadratic drag. Can. J. Phys. 88: 623–626 (2010)

