Integración numérica

Antes de introducir al lector en al cálculo del área comprendida entre una función y=f(x) y el eje X en un intervalo dado [a,b]. Vamos a ver como se calcula el área de un polígono como suma de las áreas de trapecios.

Areas

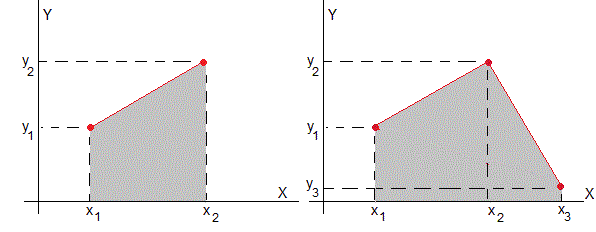
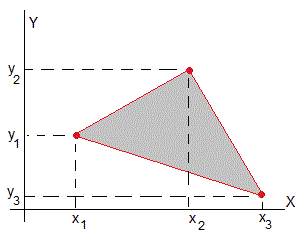
El área del trapecio de la figura de la izquierda es la suma de dos áreas: un rectángulo y un triángulo

(x₂-x₁)·y₁+(x₂-x₁)·(y₂-y₁)/2=(x₂-x₁)·(y₂+y₁)/2

El área de la figura de la derecha formada por los puntos (x₁,y₁), (x₂,y₂) y (x₃,y₃) es

(x₂-x₁)·(y₂+y₁)/2+(x₃-x₂)·(y₃+y₂)/2

Para n puntos, el área es

$A = \frac{1}{2} \sum_{i = 1}^{n - 1} (x_{i + 1} - x_{i}) (y_{i + 1} + y_{i})$

Desplazamiento de un móvil

En un movimiento rectilíneo el desplazamiento de un móvil es

$x - x_{0} = \int_{t_{0}}^{t} v \cdot d t$

Hemos generado una tabla de la velocidad de un móvil mediante la función v=exp(-t/10) m/s entre 0 y 20 s

t(s)	0	1	2	3	4	5	6	7	8	9
v(m/s)	1.00	0.90	0.82	0.74	0.67	0.61	0.55	0.50	0.45	0.41

t(s)	10	11	12	13	14	15	16	17	18	19	20
v(m/s)	0.38	0.33	0.30	0.27	0.25	0.22	0.20	0.18	0.16	0.15	0.13

La representación gráfica de la velocidad en función del tiempo es

t=0:20;
%datos generados mediante la función exp(-t/10)
v=[1,0.90, 0.82, 0.74, 0.67, 0.61, 0.55, 0.50, 0.45, 0.41, 0.38, 0.33, 0.30, 
0.27, 0.25, 0.22, 0.20, 0.18, 0.16, 0.15, 0.13];
hold on
fplot(@(t) exp(-t/10),[0,20])
plot(t,v,'ro','markersize',3,'markerfacecolor','r')
hold off
grid on
legend('exacta', 'aprox.','location','best')
xlabel('t')
ylabel('v')
title('Velocidad')

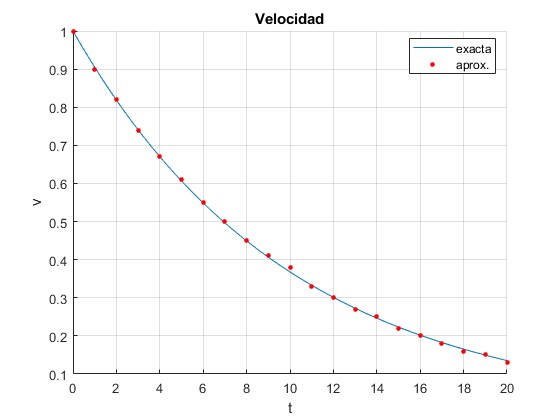
Los puntos de color rojo representan los datos experimentales

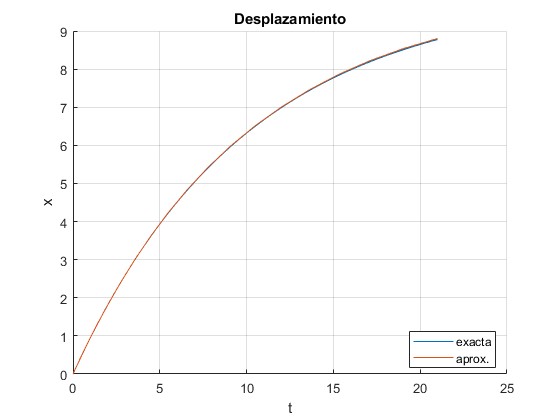
Calculamos el desplazamiento del móvil en función del tiempo mediante cumtrapz.

Representamos el desplazamiento exacto y el aproximado en función del tiempo

$x = \int_{0}^{t} \exp (- \frac{t}{10}) \cdot d t = 10 (1 - \exp (- \frac{t}{10}))$

t=0:20;
%datos generados mediante la función exp(-t/10)
v=[1,0.90, 0.82, 0.74, 0.67, 0.61, 0.55, 0.50, 0.45, 0.41, 0.38, 0.33,
 0.30, 0.27, 0.25, 0.22, 0.20, 0.18, 0.16, 0.15, 0.13];
hold on
fplot(@(t) 10*(1-exp(-t/10)), [0,20])
x=cumtrapz(v);
plot(t,x)
hold off
grid on
title('Desplazamiento')
legend('exacta', 'aprox.','location','best')
xlabel('t')
ylabel('x')

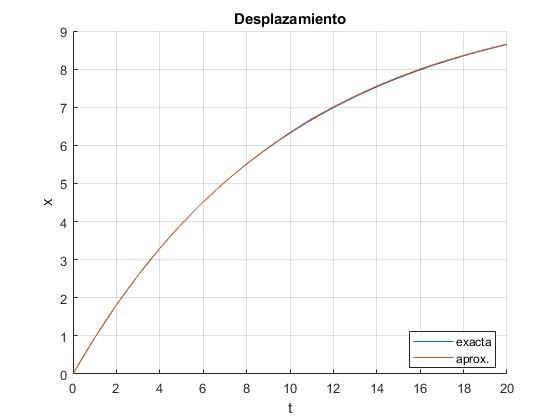
El desplazamiento total aproximado se calcula mediante trapz, muy próximo al exacto 8.6466 m

>> trapz(v)
ans =    8.6550
>> x(end)
ans =    8.6550
>> 10*(1-exp(-2))
ans =    8.6466

Datos no espaciados regularmente

Puede ocurrir que los datos del tiempo no estén espaciados por una cantidad constante, como en el ejemplo anterior

t(s)	0	0.1	0.3	0.6	1.1	1.5	2.1	2.8	3.6	4.5
v(m/s)	1.00	0.99	0.97	0.94	0.90	0.86	0.81	0.76	0.70	0.64

t(s)	5.5	6.6	7.8	9.1	10.5	12.0	13.6	15.3	17.1	19.0	21
v(m/s)	0.58	0.52	0.46	0.40	0.35	0.30	0.26	0.22	0.18	0.15	0.12

La representación gráfica de la velocidad en función del tiempo es

t=[0,0.1,0.3,0.6,1.1,1.5,2.1,2.8,3.6,4.5,5.5,6.6,
7.8,9.1,10.5,12,13.6,15.3,17.1,19,21];
%datos generados mediante la función exp(-t/10)
v=[1.00, 0.99, 0.97, 0.94, 0.90, 0.86, 0.81, 0.76, 0.70, 0.64, 0.58, 
0.52, 0.46, 0.40, 0.35, 0.30, 0.26, 0.22, 0.18, 0.15 0.12];
hold on
fplot(@(t) exp(-t/10),[0,21])
plot(t,v,'ro','markersize',3,'markerfacecolor','r')
hold off
grid on
legend('exacta', 'aprox.','location','best')
xlabel('t')
ylabel('v')
title('Velocidad')

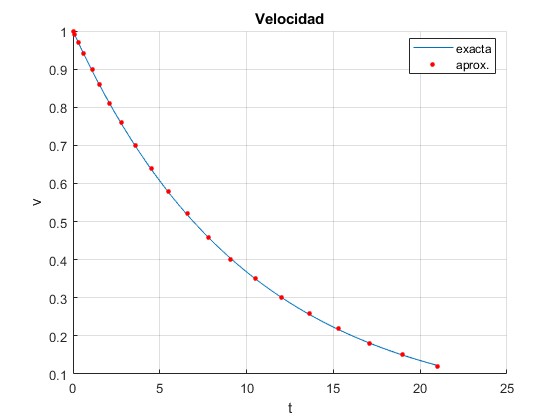
Los puntos de color rojo representan los datos experimentales

Calculamos el desplazamiento del móvil en función del tiempo mediante la función area que hace una tarea similar a cumtrapz.

Representamos el desplazamiento exacto y el aproximado en función del tiempo

function desplazamiento
    t=[0,0.1,0.3,0.6,1.1,1.5,2.1,2.8,3.6,4.5,5.5,6.
6,7.8,9.1,10.5,12,13.6,15.3,17.1,19,21];
    %datos generados mediante la función exp(-t/10)
    v=[1.00, 0.99, 0.97, 0.94, 0.90, 0.86, 0.81, 0.76, 0.70, 0.64, 
0.58, 0.52, 0.4584, 0.40, 0.35, 0.30, 0.26, 0.22, 0.18, 0.15 0.12];
    hold on
    fplot(@(t) 10*(1-exp(-t/10)), [0,21])
    xx=area();
    plot(t,xx)
    hold off
    grid on
    title('Desplazamiento')
    legend('exacta', 'aprox.','location','best')
    xlabel('t')
    ylabel('x')

    function x=area()
        x=zeros(1,length(t));
        x(1)=0;
        for k=2:length(t)
            x(k)=x(k-1)+(t(k)-t(k-1))*(v(k-1)+v(k))/2;
        end
    end

end

Area de un polígono

El área del triángulo formado por tres puntos (x₁,y₁), (x₂,y₂) y (x₃,y₃) es

(x₂-x₁)·(y₂+y₁)/2+(x₃-x₂)·(y₃+y₂)/2-(x₃-x₁)·(y₃+y₁)/2=(x₂-x₁)·(y₂+y₁)/2+(x₃-x₂)·(y₃+y₂)/2+(x₁-x₃)·(y₁+y₃)/2

Para un polígono de n lados, formado por los puntos (x₁,y₁), (x₂,y₂) ... (x_n,y_n) el área se calcula mediante la fórmula

$A = \frac{1}{2} ((x_{1} - x_{n}) (y_{1} + y_{n}) + \sum_{1}^{n - 1} (x_{i + 1} - x_{i}) (y_{i + 1} + y_{i}))$

Para cerrar la figura poligonal, añadimos el vértice n+1, que coincide con el primer vértice (x₁,y₁), (x₂,y₂) ... (x_n,y_n), (x₁,y₁). El cálculo del área se simplifica

$A = \frac{1}{2} (\sum_{1}^{n} (x_{i + 1} - x_{i}) (y_{i + 1} + y_{i}))$

Consideremos primero un polígono regular, un pentágono. Calculamos el área mediante la función MATLAB polyarea y también, mediante la fórmula que hemos obtenido anteriormente

n=5; %número de lados
radio=3; %radio de la circunferencia 
x=radio*cos((0:n)*2*pi/n);
y=radio*sin((0:n)*2*pi/n);
%las coordenadas del último vértice son las del primer vértice
hold on
fill(x,y,'y')
plot(x,y,'-ro', 'markersize',4,'markeredgecolor','r','markerfacecolor','r')
hold off
xlabel('x')
ylabel('y')
axis equal
area=0;
for i=1:n
    area=area+(x(i+1)-x(i))*(y(i+1)+y(i))/2;
end
area=abs(area)
title (['Area del polígono regular: ' num2str(polyarea(x,y))])

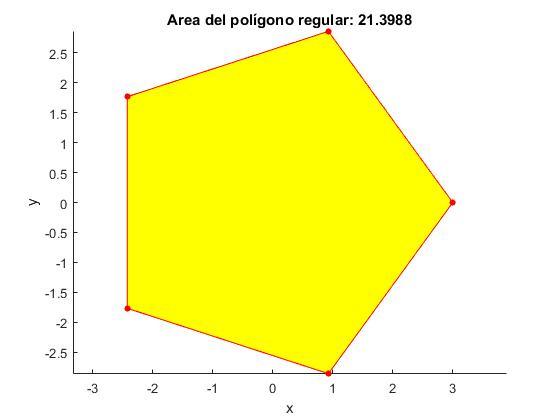
area =   21.3988

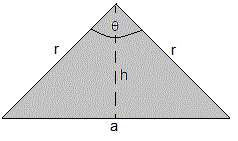
El área de un polígono regular de n inscrito una circunferencia de radio r es la suma del área de n triángulos isósceles de vértice θ=2π/n.

A=n·(a·h)/2

Como vemos en la figura

$\begin{array}{l} a = 2 \cdot r \cdot \sin (\frac{θ}{2}) h = r \cdot \cos (\frac{θ}{2}) \\ A = n \frac{a h}{2} = \frac{1}{2} n r^{2} \sin θ = \frac{1}{2} n r^{2} \sin (\frac{2 π}{n}) \end{array}$

>> area=n*radio^2*sin(2*pi/n)/2
area =   21.3988

Consideramos ahora, un polígono cualesquiera

x = [15,13,5,4,0,0,1,4,5,7,9,12,14,13,15,15];
y = [1,0,1,2,4,4,7,8,10,11,10,9,8,4,4,1];
%las coordenadas del último vértice son las del primer vértice
hold on
fill(x,y,'y')
plot(x,y,'-ro', 'markersize',4,'markeredgecolor','r','markerfacecolor','r')
hold off
xlabel('x')
ylabel('y')
axis equal
area=0;
for i=1:length(x)-1
    area=area+(x(i+1)-x(i))*(y(i+1)+y(i))/2;
end
title (['Area del polígono: ' num2str(area])

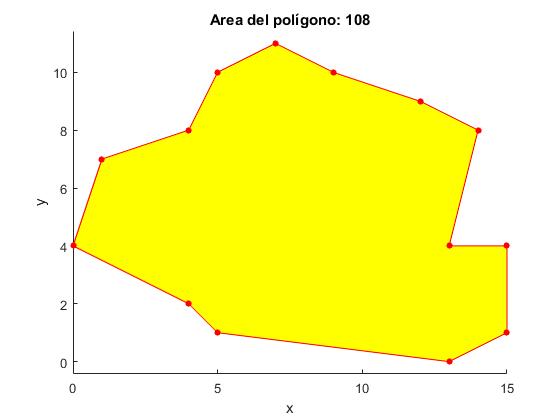
La función MATLAB polyarea solamente precisa los n vértices del polígono, dos vectores x e y de dimensión n

>> x = [15,13,5,4,0,0,1,4,5,7,9,12,14,13,15];
>> y = [1,0,1,2,4,4,7,8,10,11,10,9,8,4,4];
>> polyarea(x,y)
ans =   108

Método del punto medio

El método del punto medio es muy fácil de entender, ya que aproxima la integral definida

$\int_{a}^{b} f (x) d x$

a la suma del área de pequeños rectángulos. Como se ve en la figura el área de cada rectángulo es f(x_m) ·Δx_i, donde x_m=(x_i+1+x_i)/2 es la posición intermedia entre x_i y x_i+1.

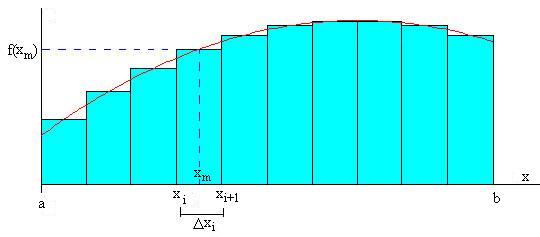
Definimos la función integral_2 para que realice las siguientes tareas:

Calcula la posición intermedia x_m=(x_i+1+x_i)/2 entre x_iy x_i+1
Calcula el área del rectángulo f(x_m) ·Δx_i, donde Δx_i=x_i+1-x_i
Calcula el área total aproximada en el intervalo a, b.

function suma=integral_2(f,x)
    suma=0;
    for i=1:length(x)-1
        xm=(x(i+1)+x(i))/2;
        suma=suma+f(xm)*(x(i+1)-x(i));
    end
end

En el script llamamos a integral_2

t0=input('tiempo inicial, t0: ');
tf=input('tiempo final, tf: ');
n=input('número intervalos, n: ');

vel=@(t) -t.^2+14*t+21;  %función velocidad
t1=linspace(t0,tf,n+1);
res=integral_2(vel,t1); %calcula la integral
fprintf('El desplazamiento es: %3.2f\n',res)

En la ventana de comandos corremos el script

tiempo inicial, t0: 0
tiempo final, tf: 10
número intervalos, n: 10
El desplazamiento es: 577.50

Fórmula del trapecio

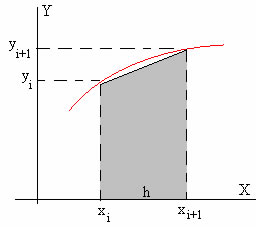
Para calcular la integral definida de la función f(x) en el intervalo comprendio entre x₀ y x, dividimos este intervalo en pequeños intervalos de longitud h=x_i+1-x_i. Sustituimos la función por la recta que une los puntos (x_i, y_i) y (x_i+1, y_i+1). El área sombreada en la figura es la suma del área de un rectángulo más el área de un triángulo, vale

$h \cdot y_{i} + \frac{1}{2} h \cdot (y_{i + 1} - y_{i}) = \frac{1}{2} h \cdot (y_{i + 1} + y_{i})$

El área total aproximada bajo la curva es

$\begin{array}{l} \frac{h}{2} (y_{1} + y_{2}) + \frac{h}{2} (y_{2} + y_{3}) + \frac{h}{2} (y_{3} + y_{4}) + ... + \frac{h}{2} (y_{n - 2} + y_{n - 1}) + \frac{h}{2} (y_{n - 1} + y_{n}) = \\ \frac{h}{2} (y_{1} + 2 y_{2} + 2 y_{3} + 2 y_{4} + ... + 2 y_{n - 2} + 2 y_{n - 1} + y_{n}) \end{array}$

Definimos en la función trapecio el procedimiento. Donde f es la función integrando y x el vector de n+1 datos comprendidos entre la abscisa inicial x0 y la final xf ambas incluidas, si el número de intervalos es n.

function sum=trapecio(f,x0, xf, nInterv)
    %el número de puntos es n intervalos más uno
    x=linspace(x0,xf,nInterv+1);
    n=length(x);    
    sum=(f(x(1))+f(x(n)))/2;
    for i=2:n-1
        sum=sum+f(x(i));
    end
    sum=sum*(x(2)-x(1));
end

Dada la función integrando f(x), calculamos la aproximación a la integral definida en el intervalo comprendido entre x₀ y x_f.

x0=input('abscisa inicial, x0: ');
xf=input('abscisa final, xf: ');
n=input('número intervalos, n: ');

deriv=@(x) -x^2+14*x+21;  %definición del integrando 
res=trapecio(deriv,x0,xf,n); %calcula la integral
fprintf('El valor aproximado de la integral: %3.2f\n',res)

En la ventana de comandos corremos el script

abscisa inicial, x0: 0
abscisa final, xf: 10
número intervalos, n: 10
El valor aproximado de la integral: 575.00

La función trapecio hace los mismo que la función trapz de MATLAB

x0=0;
xf=10;
n=10;
deriv=@(x) -x.^2+14*x+21;  %definición del integrando 
x=linspace(x0,xf,n+1);
y=deriv(x);
disp(trapz(x,y))

El método de Simpson (1/3)

En este procedimiento, se toma el intervalo de anchura 2h, comprendido entre x_i y x_i+2, y se sustituye la función f(x) por la parábola que pasa por tres puntos (x_i, y_i), (x_i+1, y_i+1), y (x_i+2, y_i+2).

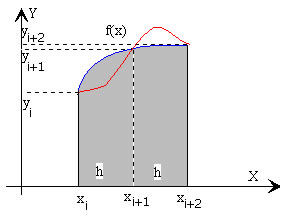
Calculamos la contribución a la integral del primer intervalo (x₀, x₀+2h) y generalizaremos para el resto de los intervalos.

La ecuación de la parábola y=ax²+bx+c que pasa por los puntos (x₀, y₀), (x₀+h, y₁), (x₀+2h, y₂) es

$\begin{array}{l} y_{0} = a x_{0}^{2} + b x_{0} + c \\ y_{1} = a {(x_{0} + h)}^{2} + b (x_{0} + h) + c \\ y_{2} = a {(x_{0} + 2 h)}^{2} + b (x_{0} + 2 h) + c \end{array}$

Este sistema de tres ecuaciones con tres incógnitas, se reduce a

$\begin{array}{l} y_{1} = y_{0} + 2 a x_{0} h + a h^{2} + b h \\ y_{2} = y_{0} + 4 a x_{0} h + 4 a h^{2} + 2 b h \end{array}$

Despejamos el coeficiente a, y 2ax₀+b

$a = \frac{y_{2} - 2 y_{1} + y_{0}}{2 h^{2}} 2 a x_{0} + b = \frac{4 y_{1} - 3 y_{0} - y_{2}}{2 h}$

Sustituimos la curva por la porción de parábola en el intervalo (x₀, x₀+2h). La integral vale.

$\begin{array}{l} I = \int_{x_{0}}^{x_{0} + 2 h} (a x^{2} + b x + c) d x = \frac{a}{3} (6 x_{0}^{2} + 12 x_{0} h^{2} + 8 h^{3}) + \frac{b}{2} (4 x_{0} h + 4 h^{2}) + c (2 h) = \\ 2 h (a x_{0}^{2} + b x_{0} + c) + 2 (2 a x_{0} + b) h^{2} + \frac{8}{3} a h^{3} = \\ \frac{h}{3} (y_{0} + 4 y_{1} + y_{2}) \end{array}$

En general, el valor del área aproximada, en el intervalo (x_i, x_i+2h) sombreada en la figura, es

$\frac{h}{3} (y_{i} + 4 y_{i + 1} + y_{i + 2})$

El área aproximada en el intervalo (a, b) es

$\int_{a}^{b} f (x) \cdot d x \approx \frac{h}{3} (y_{0} + 4 y_{1} + y_{2}) + \frac{h}{3} (y_{2} + 4 y_{3} + y_{4}) + .... + \frac{h}{3} (y_{n - 2} + 4 y_{n - 1} + y_{n})$

o bien, agrupando términos

$\int_{a}^{b} f (x) \cdot d x \approx \frac{h}{3} ((y_{0} + y_{n}) + 4 (y_{1} + y_{3} + .... y_{n - 1}) + 2 (y_{2} + y_{4} + .... y_{n - 2}))$

El primer paréntesis, contiene la suma de los extremos, el segundo, la suma de los términos de índice impar, y el tercero la suma de los términos de índice par. En el método de Simpson, el número de divisiones n debe de ser par.

Definimos en la función simpson el procedimiento. Donde f es la función integrando y x el vector de n+1 datos comprendidos entre la abscisa inicial x0 y la final xf ambas incluidas, si el número de intervalos es n que tiene que ser un número PAR.

function suma=simpson(f,x0,xf,n)
%n número par de intervalos, n+1 número de puntos en el vector    
    x=linspace(x0,xf,n+1);   
    h=x(2)-x(1);
    suma=f(x(1))+f(x(n+1));
    for i=2:2:n
            suma=suma+4*f(x(i));
        end
        for i=3:2:n-1
            suma=suma+2*f(x(i));
        end
        suma=suma*h/3;
end

Dada la función integrando f(x), calculamos la aproximación a la integral definida en el intervalo comprendido entre x₀ y x

x0=input('abscisa inicial, x0: ');
xf=input('abscisa final, xf: ');
n=input('número intervalos (par), n: ');
if rem(n,2)==1
  disp('El número intervalos tiene que ser par ');
  break
end

deriv=@(x) -x^2+14*x+21;  %definición del integrando 
res=simpson(deriv,x0,xf,n); %calcula la integral
fprintf('El valor aproximado de la integral: %3.2f\n',res)

En la ventana de comandos corremos el script

abscisa inicial, x0: 0
abscisa final, xf: 10
número intervalos, n: 10
El valor aproximado de la integral: 576.67

Apreciamos la mejora en el resultado de la integral con el método de Simpson.

Existe una versión del método de Simpson denominada 3/8 en el que se emplea una ecuación cúbica para concectar cuatro puntos.

Integrales impropias

Consideremos una función f(x) que se hace infinita cuando x→a, vamos a calcular la integral definida

$\int_{a}^{b} f (x) d x$

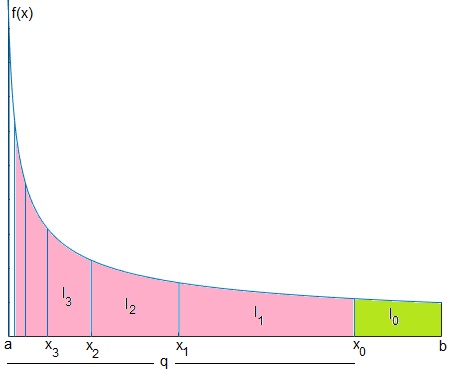
Para dibujar parte de la figura se ha empleado el código

f=@(x) 1./sqrt(x);
fplot(f,[0.01,1])
a=0;
b=1;
x0=0.8;
q=x0-a;
r=0.5;
for j=0:6
    xx=a+r^j*q;
    line([xx,xx],[0,f(xx)])
end
ylim([0,10])
xlabel('x')
ylabel('f(x)')
title('Integral impropia')

Se elige un punto x₀ cercano a a, se calcula la integral

$I_{0} = \int_{x_{0}}^{b} f (x) d x$

que es el área sombreada de color verde claro

Se divide el intervalo [a,x₀] en intervalos cada vez más pequeños tal como se aprecia en la figura

$\begin{array}{l} x_{j} = a + r^{j} q, r < 1, j = 1,2,3... \\ q = x_{0} - a \end{array}$

Cuando el índice j→∞, x_∞=a, ya que r<1

La integral definida es la suma de infinitas integrales parciales

$I = \int_{x_{0}}^{b} f (x) d x + \sum_{j = 1}^{\infty} \int_{x_{j}}^{x_{j - 1}} f (x) d x$

Ejemplo

$I = \int_{1}^{2} \frac{1}{\sqrt{x^{4} - 1}} d x$

f(x)→∞ cuando x→1

f=@(x) 1./sqrt(x.^4-1);
fplot(f,[1,2])
ylim([0,10])
grid on
xlabel('x')
ylabel('f(x)')
title('Integral impropia')

Pra calcular el área bajo la curva en el intervalo a=1, b=2, tomamos x₀=1.1, q=x₀-a=0.1, r=0.1

$\begin{array}{l} I = \int_{1}^{2} \frac{1}{\sqrt{x^{4} - 1}} d x = \int_{x_{0}}^{2} \frac{1}{\sqrt{x^{4} - 1}} d x + \sum_{j = 1}^{\infty} \int_{x_{j}}^{x_{j - 1}} \frac{1}{\sqrt{x^{4} - 1}} d x, {\begin{cases} x_{0} = 1.1 \\ x_{j} = 1 + {0.1}^{j} \cdot 0.1 \end{cases} \\ = \int_{1.1}^{2} \frac{1}{\sqrt{x^{4} - 1}} d x + \int_{1.01}^{1.1} \frac{1}{\sqrt{x^{4} - 1}} d x + \int_{1.001}^{1.01} \frac{1}{\sqrt{x^{4} - 1}} d x + \int_{1.0001}^{1.001} \frac{1}{\sqrt{x^{4} - 1}} d x + ... \end{array}$

Uilizamos el método de Simpson tomando n=100, para calcular cada una de las integrales parciales

function impropio_1
    f=@(x) 1/sqrt(x^4-1);
    a=1; %límites
    b=2;
    x0=1.1; %punto cercano a a
    q=x0-a;
    r=0.1;
    In=simpson(f, x0, b,100);
    format long;
    disp([a,x0, In])
    for j=1:6
        x1=a+r^j*q;
        x2=a+r^(j-1)*q;
        Ip=simpson(f, x1, x2,100);
        In=In+Ip;
        disp([x1,x2,Ip, In])
    end

    function suma=simpson(f,x0,xf,n)
    %n número par de intervalos, n+1 número de puntos en el vector    
        x=linspace(x0,xf,n+1);   
        h=x(2)-x(1);
        suma=f(x(1))+f(x(n+1));
        for i=2:2:n
            suma=suma+4*f(x(i));
        end
        for i=3:2:n-1
            suma=suma+2*f(x(i));
        end
        suma=suma*h/3;
    end
end

   1.000000000000000   1.100000000000000   0.499282654973372
   1.010000000000000   1.100000000000000   0.208786134108676   0.708068789082049
   1.001000000000000   1.010000000000000   0.068135824274669   0.776204613356718
   1.000100000000000   1.001000000000000   0.021615126440058   0.797819739796776
   1.000010000000000   1.000100000000000   0.006837481317325   0.804657221114101
   1.000001000000000   1.000010000000000   0.002162270338617   0.806819491452718
   1.000000100000000   1.000001000000000   0.000683772104262   0.807503263556980

Hemos probado con siete intervalos. La primera y segunda columna son los intervalos de integración, la tercera columna son los resultados de las integrales parciales, la cuarta columna la suma acumulada. El valor aproximado de la integral definida es el último elemento de la cuarta columna, 0.807503263556980

MATLAB dispone de la función integral para calcular las integrales definidas, como veremos en la página titulada Integración numérica con MATLAB

>> f=@(x) 1./sqrt(x.^4-1);
>> integral(f,1,2)
ans =   0.807819333968784

Ejemplos en el Curso de Física

Hay muchos ejemplos en las que se utiliza la función integral de MATLAB. Sin embargo, hay un ejemplo significativo en la página titulada Trayectorias de persecución (II), en la que se muestra los pasos a siguir para integrar la ecuación diferencial x=f(dy/dx) definida de forma implícita, con el fin de determinar la expresión de la trayectoria de persecución y=g(x) de forma numérica

Referencias

F. A. Herrero. Routine for improper integrals with a programmable calculator. Am. J. Phys. 48 (8) August 1980. pp. 679-681