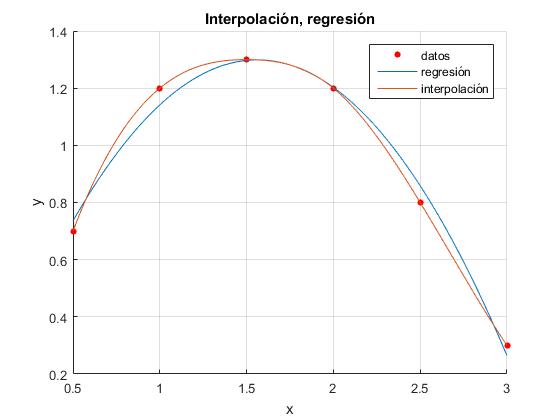
Interpolación
Este pequeño programa muestra la diferencia entre interpolación y regresión
x=0.5:0.5:3;
y=[0.7,1.2,1.3,1.2,0.8,0.3];
hold on
plot(x,y,'ro','markersize',4,'markerfacecolor','r')
%regresión
p=polyfit(x,y,2); %polinomio de segundo grado
z=@(xx) polyval(p,xx);
fplot(z,[x(1),x(end)])
%interpolación
z=@(xx) spline(x,y,xx);
fplot(z,[x(1),x(end)])
hold off
grid on
legend('datos','regresión','interpolación')
xlabel('x')
ylabel('y');
title('Interpolación, regresión')
Interpolación lineal
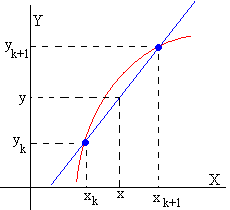
La interpolación lineal es muy sencilla. Disponemos de pares de datos (xk,yk) k=1,2...n. Queremos conocer el valor de y para un valor cualesquiera de x en el intervalo x1 a xn. Supongamos que x está en el intervalo (xk,xk+1) tal como se muestra en la figura. Trazamos la recta que pasa por los puntos (xk,yk) y (xk+1,yk+1), cuya ecuación es
Creamos la función
function y0 = interpola_lineal(x,y,x0)
y0=zeros(length(x0),1);
for j=1:length(x0)
indice=find(x>x0(j));
k=indice(1)-1;
y0(j)=((x0(j)-x(k))*y(k+1)-(x0(j)-x(k+1))*y(k))/(x(k+1)-x(k));
end
end
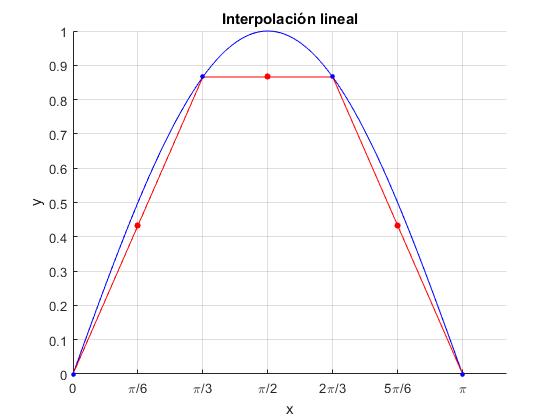
Probamos la función para interpolar linealmente los siguientes pares de datos (0,0), (π/3, sin(π/3)), (2π/3, sin(2π/3)),(π, 0). Comprobamos que obtenemos los mismos resultado utilizando la función MATLAB
x=0:pi/3:pi; %datos
y=sin(x);
x0=[pi/6,pi/2,5*pi/6]; %interpolación lineal
y0=interpola_lineal(x,y,x0);
%y0=interp1(x,y,x0,'linear'); %esta es una función MATLAB
hold on
fplot('sin(x)',[0,pi])
plot(x,y)
plot(x,y,'bo','markersize',3,'markerfacecolor','b')
plot(x0,y0,'ro','markersize',4,'markerfacecolor','r')
set(gca,'XTick',0:pi/6:pi)
set(gca,'XTickLabel',{'0','\pi/6','\pi/3','\pi/2','2\pi/3','5\pi/6','\pi'})
hold off
grid on
xlabel('x');
ylabel('y')
title('Interpolación lineal')
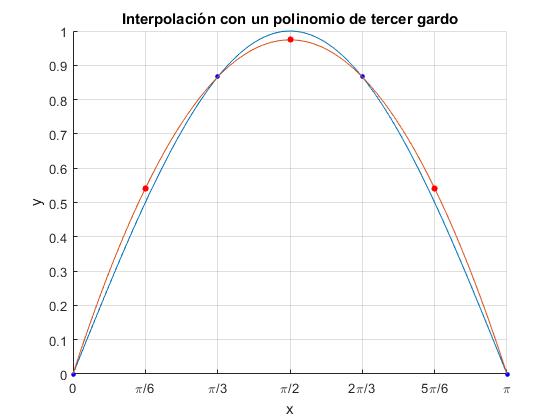
Interpolación por un polinomio de grado n
Calculamos los coeficientes de un polinomio de tercer grado y=a1x3+a2x2+a3x+a4 que pase por los cuatro puntos. Obtenemos un sistema de cuatro ecuaciones con cuatro incógnitas.
x=[0,pi/3,2*pi/3,pi]; %datos
y=sin(x);
xx=0:pi/90:pi; %función
yy=sin(xx);
x0=[pi/6,pi/2,5*pi/6]; %interpolación lineal
A=vander(x);
p=A\y'; %coeficientes del polinomio
hold on
fplot('sin(x)',[0,pi]) % función
plot(x,y,'bo','markersize',3,'markerfacecolor','b')
z=@(xx) polyval(p,xx); %polinomio
fplot(z,[0,pi])
y0=polyval(p,x0); %valores interpolados
plot(x0,y0,'ro','markersize',4,'markerfacecolor','r')
set(gca,'XTick',0:pi/6:pi)
set(gca,'XTickLabel',{'0','\pi/6','\pi/3','\pi/2','2\pi/3','5\pi/6','\pi'})
hold off
xlabel('x');
ylabel('y')
grid on
title('Interpolación con un polinomio de tercer gardo')
Interpolación de Lagrange
Queremos encontrar los coeficientes de un polinomio de grado N
a1xN+a2xN-1+...+aNx+aN+1
que pase por todos los pares de datos (x1,y1), (x2,y2), ...(xN+1,yN+1). Los coeficientes se pueden obtener resolviendo el sistema de ecuaciones:
En forma matricial
Esta matriz se conoce con el nombre de Vandermonde y se construye con el comando
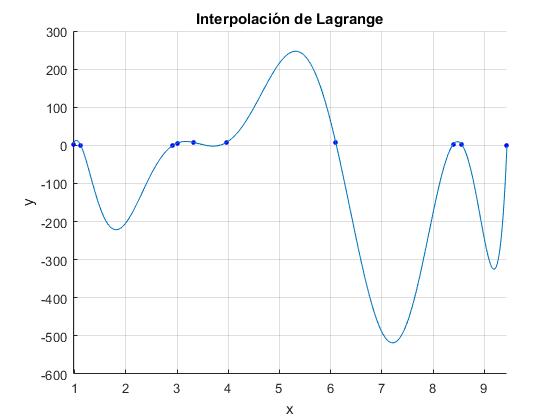
Sea la siguiente tabla de datos tomada de una experiencia
| x | 0.97 | 1.12 | 2.92 | 3.00 | 3.33 | 3.97 | 6.10 | 8.39 | 8.56 | 9.44 |
|---|---|---|---|---|---|---|---|---|---|---|
| y | 2.58 | 0.43 | 0.06 | 5.74 | 7.44 | 8.07 | 6.37 | 2.51 | 1.44 | 0.52 |
Cuando el número N+1 de datos es relativamente pequeño, las primeras columnas de la matriz A pueden guardar números muy grandes, los efectos del redondeo pueden afectar al valor de los coeficientes ai del polinomio.
Los valores del polinomio se puede obtener también utilizando la función
x=[0.97 1.12 2.92 3.00 3.33 3.97 6.10 8.39 8.56 9.44];
y=[2.58 0.43 0.06 5.74 7.44 8.07 6.37 2.51 1.44 0.52];
n=length(x); %número de pares de datos
%A=vander(x);
A=zeros(n); %líneas equivalentes a utilizar vander(x)
for j=1:n
A(:,j)=(x').^(n-j);
end
p=A\y'; %sistema de ecuaciones lineales, y' es vector columna
%p=polyfit(x,y,n-1) %n-1 es el grado del polinomio
z=@(xx) polyval(p,xx);
hold on
plot(x,y,'bo','markersize',3,'markerfacecolor','b')
fplot(z,[x(1),x(end)])
xlabel('x')
ylabel('y')
grid on
title('Interpolación de Lagrange');
hold off
El script presenta opciones: La matriz
Warning: Polynomial is badly conditioned. Add points with distinct X values, reduce the degree of the polynomial, or try centering and scaling as described in HELP POLYFIT. > In polyfit (line 75) In xxx (line 11) p = 1.0e+04 * 0.0000 -0.0003 0.0057 -0.0595 0.3782 -1.4951 3.6430 -5.2142 3.9256 -1.1823
Un polinomio de Lagrange LN(x) de grado N es la expresión
Este polinomio pasa por todos los puntos (xi,yi).
Elaboramos una función denominada
function yy = lagrange_3(x,y,xx)
n = length(x);
for i=1:n
w(i)=prod(xx-x([1:i-1 i+1:n]))*y(i)/prod( x(i)-x([1:i-1 i+1:n]) ) ;
end
yy=sum(w);
end
Llamamos a la función
>> x=[0.97 1.12 2.92 3.00 3.33 3.97 6.10 8.39 8.56 9.44]; >> y=[2.58 0.43 0.06 5.74 7.44 8.07 6.37 2.51 1.44 0.52]; >> yy=lagrange_3(x,y,1.0) yy = 10.0725 >> yy=lagrange_3(x,y,2.0) yy = -203.7000
Alternativamente, elaboramos una función denominada
function p=lagrange_p(x,y)
n=length(x); %n-1 es el grado del polinomio
if length(y)~=n
error('x e y tienen que tener la misma longitud')
end
p=zeros(1,n);
for i=1:n
pol=[y(i)];
for j=1:n
if(i~=j)
%multiplica un polinomio por un binomio
pol=conv([1 -x(j)],pol)/(x(i)-x(j));
end
end
p=p+pol;
end
end
Para obtener el producto de los binomios del numerador de cada término, utilizamos la función
>> p1=[1 0 -2 -4]; >> p2=[1 3 4]; >> p=conv(p1,p2) p = 1 3 2 -10 -20 -16
Utilizamos la función
>> x=[0.97 1.12 2.92 3.00 3.33 3.97 6.10 8.39 8.56 9.44]; >> y=[2.58 0.43 0.06 5.74 7.44 8.07 6.37 2.51 1.44 0.52]; >> p=lagrange_p(x,y) p = 1.0e+004 * 0.0000 -0.0003 0.0057 -0.0595 0.3782 -1.4951 3.6430 -5.2142 3.9256 -1.1823
Obtenemos el mismo resultado, que resolviendo el sistema de N+1 ecuaciones lineales.
Una vez obtenido el polinomio de Lagrange calculamos el valor de y para valores de x que no están en la tabla.
>> xx=[1.0 2.0 3.5]; >> yy=polyval(p,xx) yy = 10.0725 -203.7000 1.8338
Comparación
Como vamos a apreciar, la interpolación de Lagrange es un interesante ejercicio de programación, pero no poduce buenos resultados. Para probarlo, vamos a tomar nueve puntos de una función igualmente espaciados y vamos a comparar la gráfica de la función y la interpolación de los nueve puntos por el procedimiento de Lagrange. En la siguiente sección, explicamos un procedimiento mucho más exacto, los splines
Vamos a probar este procedimiento de interpolación, tomando nueve puntos equidistantes de la función
Ahora interpolamos mediante un polinomio de grado n-1 (ocho) que pasa por los n (nueve) puntos (xi,yi)
x=-4:4;
f=@(x) sin(x)/(1+x^2);
%dibuja los puntos
hold on
plot(x,y,'bo','markersize',3,'markeredgecolor','b','markerfacecolor','b')
n=length(x);
p=polyfit(x,y,n-1); %polinomio que pasa por los puntos
%p=lagrange_p(x,y); %se obtiene el mismo resultado
z=@(xx) polyval(p,xx);
fplot(z,[-4,4],'r')
fplot(f,[-4,4])
hold off
grid on
xlabel('x')
ylabel('y')
legend('función','interpolación')
title('Interpolación por Lagrange')
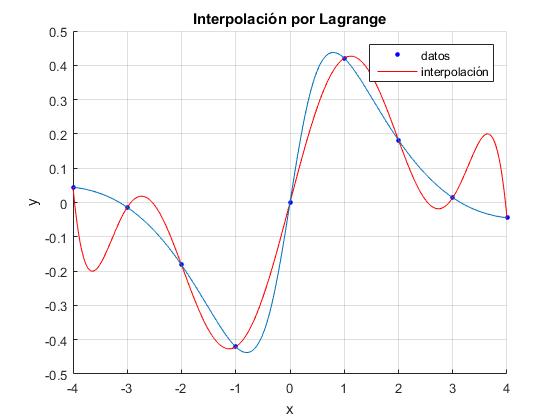
El resultado deja mucho que desear principalmente, en el primer y último intervalo.
Splines
Vamos a explicar mediante un ejemplo el procedimiento de interpolación denominado "splines", para generalizarlo después a cualquier conjunto de pares de datos.
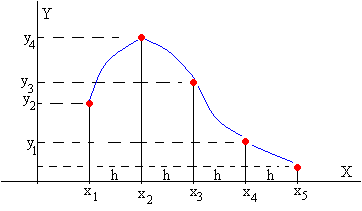
Dado el conjunto de pares de datos (x1,y1), (x2,y2), (x3,y3), (x4,y4), (x5,y5) puntos de color rojo en la figura. Definimos la función S(x)
Cada una de las funciones si(x) en color azul en la figura, es un polinomio de tercer grado, cuya primera y segunda derivada es
Para calcular las 4×4=16 incógnitas a1,a2,a3,a4, b1,b2,b3,b4, c1,c2,c3,c4, d1,d2,d3,d4, se imponen las siguientes condiciones:
- La función S(x) pasa por todos los puntos (xi,yi) i=1,2,3,4,5
- La función S(x) es continua en x2, x3, x4.
- La derivada primera de la función S(x) es continua en x2, x3, x4.
- Denominamos m1, m2, m3, m4, m5 al valor de la derivada segunda de si(x) en los puntos x1, x2, x3, x4, x5.
- La derivada segunda de S(x) es continua en los puntos x2, x3, x4
Supongamos que el espaciado entre dos puntos consecutivos es constante h=xi-xi-1, i=2,3,4,5.
Vamos a expresar las incógnitas a1,a2,a3,a4, b1,b2,b3,b4, c1,c2,c3,c4, d1,d2,d3,d4, en términos de h, el valor de las ordenadas yi y el valor de la derivada segunda de S(x), mi en cada punto xi, i=1,2,3,4,5.
De (4) y (5) expresamos a1,a2, a3, a4 en términos de m1, m2, m3, m4, m5.
Teniendo en cuenta (1) y (4), las ecuaciones (2) se expresan
Que nos permite despejar c1, c2, c3 en términos de m1, m2, m3, m4, y1, y2, y3, y4
La última ecuación de (1) nos permite despejar c4
Las ecuaciones (3) se expresan
Tenemos tres ecuaciones y cinco incógnitas m1, m2, m3, m4, m5
Fijamos los valores de la derivada segunda m1 y m5 en los puntos extremos. Supongamos que m1=0 y m5=0.
Hay otras posibilidades que se pueden consultar en el documento http://online.redwoods.edu/instruct/darnold/laproj/Fall98/SkyMeg/Proj.PDF
Despejamos m2, m3, m4 del sistema de tres ecuaciones
Caso general
En general, con n pares de datos tendremos el sistema
Fijamos los valores de los extremos del vector de las incógnitas m: m1=0, mn-1=0, a continuación, obtenemos mediante el operador división por la izquierda los valores de m2, m3, ...mn-2, finalmente, se calculan:
- los coeficientes a1,a2,a3,...an-1.
- los coeficientes b1,b2,b3,...bn-1.
- los coeficientes c1,c2,c3,...cn-1.
- los coeficientes d1,d2,d3,...dn-1.
Codificación
En primer lugar, vamos a entender como trabaja la función
>> A=[1,2,3;4,5,6;7,8,9]
A =
1 2 3
4 5 6
7 8 9
>> diag(A) %diagonal principal
ans =
1
5
9
>> diag(A,1) %diagonal superior
ans =
2
6
>> diag(A,-1) %diagonal inferior
ans =
4
8
La función
A=diag(4*ones(3,1))+diag(ones(2,1),1)+diag(ones(2,1),-1)
A =
4 1 0
1 4 1
0 1 4
La función
El vector de los términos independientes se calcula aplicando dos veces la función
Estamos en condiciones de crear un script que calcule las incógnitas m2, m3, ... mn-1, aplicando el operador división por la izquierda.
Vamos a probar este procedimiento de interpolación, tomando nueve puntos equidistantes de la función
x=-4:4;
f=@(x) sin(x)./(1+x.^2);
y=f(x);
h=x(2)-x(1); %espaciado constante
n=length(x); %número de pares de datos
%matriz de dimensión n-2
A=diag(4*ones(n-2,1))+diag(ones(n-3,1),1)+diag(ones(n-3,1),-1);
s=diff(diff(y))*6/h^2; %vector de los términos indpendientes
mm=A\s'; %vector de las incógnitas
m=[0;mm;0]; %ceros en los extremos
a=zeros(1,n-1);
b=zeros(1,n-1);
c=zeros(1,n-1);
d=zeros(1,n-1);
for i=1:n-1
a(i)=(m(i+1)-m(i))/(6*h);
b(i)=m(i)/2;
c(i)=(y(i+1)-y(i))/h-(m(i+1)+2*m(i))*h/6;
d(i)=y(i);
end
hold on
plot(x,y,'bo','markersize',3,'markeredgecolor','b','markerfacecolor','b')
for i=1:n-1
z=@(xx) a(i)*(xx-x(i)).^3+b(i)*(xx-x(i)).^2+c(i)*(xx-x(i))+d(i);
fplot(z,[x(i),x(i+1)],'r')
end
fplot(f,[-4,4])
hold off
grid on
xlabel('x')
ylabel('y')
legend('función','interpolación')
title('Interpolación por splines')
con los nueve puntos unidos mediante polinomios de tercer grado vemos que la curva interpolada y la exacta están próximas.
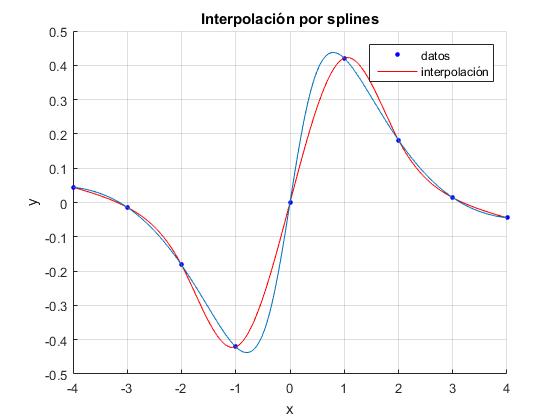
Los puntos de color azul, son los nueve pares de datos, cada una de las curvas de color rojo entre dos puntos azules consecutivos es un polinomio de tercer grado que pasa por dichos puntos y cumple las condiciones de continuidad de su derivada primera y segunda.
Función spline de MATLAB
Utilizamos la función
x=-4:4;
f=@(x) sin(x)./(1+x.^2);
y=f(x);
%dibuja los puntos
hold on
plot(x,y,'bo','markersize',3,'markeredgecolor','b','markerfacecolor','b')
z=@(xx) spline(x,y,xx); %interpolación
fplot(z,[-4,4],'r')
fplot(f,[-4,4]) %función
hold off
grid on
xlabel('x')
ylabel('y')
title('Interpolación por splines de MATLAB')
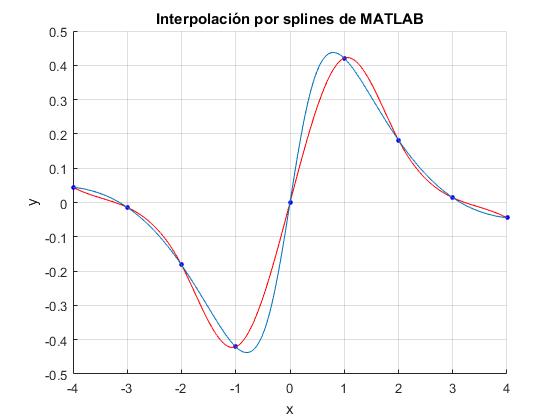
Comparando ambas gráficas, vemos que el resultado que hemos obtenido creando nuestra propia función
Aproximación de funciones mediante un polinomio
Muchas funciones matemáticas tales como
Puntos igualmente espaciados
Tomamos n valores de la función yi=f(xi) con i=1...n. y determinamos el polinomio de grado n-1 que pasa a través de los puntos (xi,yi). Sea la función
Tomamos diez abscisas xi espaciadas 0.8 en el intervalo [-4,4]. Representamos la función (en color rojo), los puntos (xi,yi) y el polinomio que pasa por dichos puntos (en color azul). Dado que la función es simétrica solamente representamos la parte positiva.
f=@(x) 1./(x.^2+1);
n=10;
a=-4;
b=4;
xx=linspace(a,b,n+1);
yy=f(xx);
p=polyfit(xx,yy,n);
x1=linspace(0,b,100);
y1=polyval(p,x1); %aproximación mediante el polinomio p
y2=f(x1); %función
hold on
plot(x1,y1,'b')
plot(x1,y2,'r')
plot(xx(xx>=0),yy(xx>=0),'ro','markersize',3,'markerfacecolor','r')
hold off
xlabel('x')
ylabel('y')
title('Aproximación de una función')
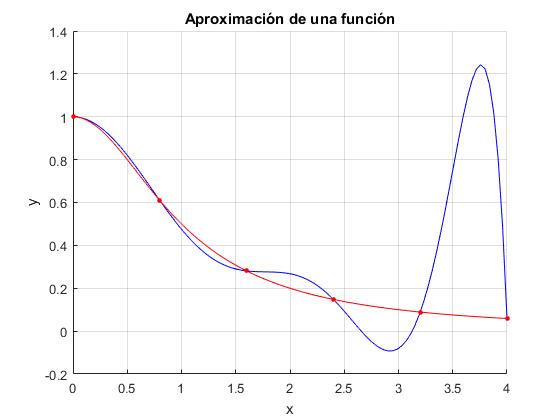
Puntos espaciados mediante la fómula de Chebyshev
Sorprendentemente, si los puntos no están igualmente espaciados, obtenemos una mejor aproximación. Si tomamos los puntos en el intervalo [a,b] espaciados de acuerdo a la fórmula denominada puntos de Chebyshev.
La función
f=@(x) 1./(x.^2+1);
lincheby=@(a,b,n) (a+b)/2+(a-b)/2*cos(pi/n*(1/2:n));
n=10;
a=-4;
b=4;
xx=lincheby(a,b,n+1);
yy=f(xx);
p=polyfit(xx,yy,n);
x1=linspace(0,b,100);
y1=polyval(p,x1); %aproximación mediante el polinomio p
y2=f(x1); %función
hold on
plot(x1,y1,'b')
plot(x1,y2,'r')
plot(xx(xx>=0),yy(xx>=0),'ro','markersize',3,'markerfacecolor','r')
hold off
xlabel('x')
ylabel('y')
title('Aproximación de una función')
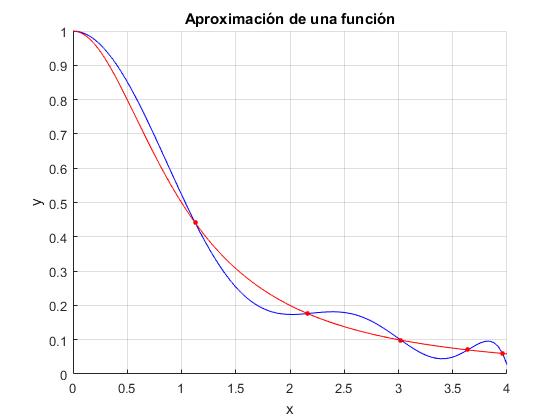
Como podemos apreciar la mejora es importante

