La cuantización de la energía es uno de los conceptos más importantes de la Mecánica Cuántica, ya que explica las propiedades de los átomos que constituyen los componentes básicos de la materia.

Para calcular los niveles de energía, es necesario resolver una ecuación diferencial de segundo orden, la ecuación de Schrödinger para la función potencial especificada, que en muchos casos carece de solución analítica sencilla. Por simplicidad, elegiremos como modelo de átomo un pozo de potencial.

La ecuación de Schrödinger independiente del tiempo en una región unidimensional cuya energía potencial viene descrita por la función E_p(x) es

${\displaystyle \frac{-{\hslash }^2}{2m}\frac{d^2\Psi }{d{x}^2}+E_p(x)\Psi =E\Psi }$

Donde E es la energía total de la partícula de masa m

${\displaystyle E=\frac{p^2}{2m}+E_p(x)}$

La solución de la ecuación de Schrödinger Ψ(x) se denomina función de onda. La función de onda se normaliza de modo que

${\displaystyle {\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{\left|\Psi (x)\right|}^{2}dx=1}}$

La simetría de la función potencial E_p(x) hace que las funciones de onda puedan ser:

• Simétricas, si Ψ(x)=Ψ(-x)
• Antisimétricas, si Ψ(x)=-Ψ(-x)

Partícula libre

El caso más simple es el de una partícula libre, la energía potencial E_p(x)=0. La ecuación de Schrödinger se escribe

${\displaystyle \frac{d^2\Psi }{d{x}^2}+\frac{2mE}{{\hslash }^2}\Psi =0}$

Su solución es

${\displaystyle \Psi (x)=A\exp (iqx)+B\exp (-iqx)q^2=\frac{2mE}{{\hslash }^2}}$

Pozo de potencial de altura infinita

Consideremos una partícula obligada a moverse en una región entre x=-a y x=a, tal como una molécula en una caja, un electrón libre en un trozo de metal, etc. Si la energía cinética del electrón es pequeña comparada con la altura de la barrera de potencial, el electrón se podrá mover libremente a través del metal pero no podrá escapar de él.

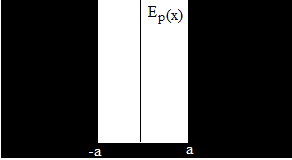
Podemos representar estas situaciones físicas, por un potencial rectangular de altura infinita. Tenemos que E_p(x)=0 para -a<x<a, ya que la partícula se mueve libremente en esta región, fuera de esta región la energía potencial se hace infinita. Entonces, cualquiera que sea el valor de le energía E de la partícula, ésta no puede estar a la izquierda de x=-a, ni a la derecha de x=a. La función de onda en dichas regiones debe de ser nula.

La ecuación de Schrödinger en la región 0<x<a donde E_p(x)=0 se escribe

${\displaystyle \frac{d^2\Psi }{d{x}^2}+\frac{2mE}{{\hslash }^2}\Psi =0}$

Su solución es

${\displaystyle \Psi (x)=A{e}^{iqx}+B{e}^{-iqx}{q}^2=\frac{2mE}{{\hslash }^2}}$

Niveles de energía

Las condiciones de contorno requieren que Ψ(x)=0 en x=-a y también, que Ψ(x)=0 en x=a.

${\displaystyle \begin{array}{l}\Psi (a)=A\exp (iqa)+B\exp (-iqa)=0\\ \Psi (-a)=A\exp (-iqa)+B\exp (iqa)=0\\ \exp (2iqa)-\exp (-iqa)=0\\ \sin (2qa)=02qa=n\pi \end{array}}$

donde n es un número entero. La energía de la partícula será

${\displaystyle E=n^2\frac{{\pi }^2{\hslash }^2}{8m{a}^2}}$

Si E₁ es la energía del primer nivel (n=1) la energía de los sucesivos niveles es 4E₁, 9E₁, 16E₁... Concluimos que la partícula no puede tener una energía arbitraria, sino valores concretos, decimos que la energía de la partícula está cuantizada.

Funciones de onda

La simetría de la función potencial E_p(x) hace que los funciones de onda sean

• Simétricas, si Ψ(x)=Ψ(-x) o bien, A=B.

Ψ(x)=2Acos(qx)

• Antisimétricas, si Ψ(x)=-Ψ(-x) o bien, A=-B.

Ψ(x)=2Aisin(qx)

En ambos casos el factor de escala, A se determina haciendo que

${\displaystyle \begin{array}{l}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\left|\Psi (x)\right|}^2=1}{\displaystyle \underset{-a}{\overset{a}{\int }}{\left|\Psi (x)\right|}^2=1}\\ {\displaystyle \underset{-a}{\overset{a}{\int }}4A^2{\cos }^2(qx)dx=}2A^2\left(2a+\frac{\sin (2qa)}{q}\right)\\ {\displaystyle \underset{-a}{\overset{a}{\int }}4A^2{\sin }^2(qx)dx=}2A^2\left(2a-\frac{\sin (2qa)}{q}\right)\end{array}}$

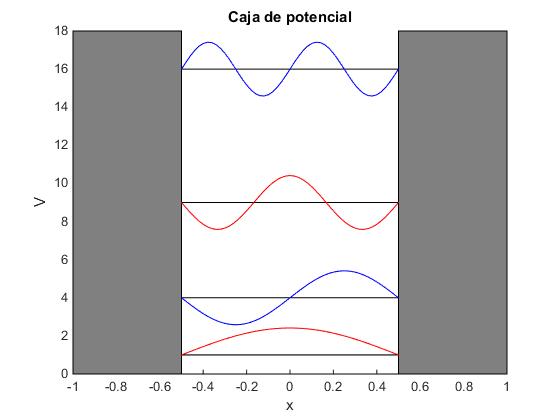
Las funciones de onda se parecen a los modos de vibración de una cuerda sujeta por ambos extremos o también denominadas ondas estacionarias.

Las funciones de onda dibujadas en color rojo, son simétricas. Las funciones de onda dibujadas en color azul, son antisimétricas

%caja de potencial
a=0.5;  %anchura de la caja 2a
Emax=18; %disminuir este valor al incrementar la anchura a
hold on
%potencial
xx=[-1 -1 -a -a a a 1 1];
yy=[0 Emax Emax 0 0 Emax Emax 0];
fill(xx,yy, [0.5 0.5 0.5])
%niveles de nergía y funciones de onda
for n=1:2:4
    %par, simétrico
    E=(n/(2*a))^2;
    line([-a a],[E E], 'color','k')
    q=n*pi/(2*a);
    suma=2*(2*a+sin(2*q*a)/q);
    x=-a:0.02:a;
    y=2*cos(q*x)/sqrt(suma);
    plot(x,E+y,'r');
    
    %impar, antisimétrico   
    E=((n+1)/(2*a))^2;
    line([-a a],[E E], 'color','k')
    q=(n+1)*pi/(2*a);
    suma=2*(2*a-sin(2*q*a)/q);
    x=-a:0.05:a;
    y=2*sin(q*x)/sqrt(suma);
    plot(x,E+y,'b');
end
hold off
xlim([-1,1])
xlabel('x');
ylabel('V')
title('Caja de potencial')

El pozo de potencial de forma rectangular

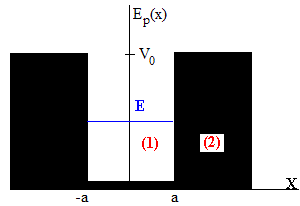
Sea un pozo de potencial de anchura 2a y de altura V₀. Situamos el origen en el centro del pozo, tal como se muestra en la figura. Las ecuaciones de Schrödinger en las regiones (1) y (2) se escriben

${\displaystyle \begin{array}{l}-\frac{{\hslash }^2}{2m}\frac{d^2\Psi }{d{x}^2}=E\Psi 0\le x\le a\\ -\frac{{\hslash }^2}{2m}\frac{d^2\Psi }{d{x}^2}+V_0\Psi =E\Psi x>a\end{array}}$

Las soluciones de estas ecuaciones son, respectivamente.

${\displaystyle \begin{array}{l}{\Psi }_1\left(x\right)=A_1\exp \left(i{q}_{1}x\right)+B_1\exp \left(-i{q}_{1}x\right)q_1=\sqrt{\frac{2mE}{{\hslash }^2}}\\ {\Psi }_2\left(x\right)=A_2\exp \left(i{q}_{2}x\right)+B_2\exp \left(-i{q}_{2}x\right)q_2=\sqrt{\frac{2m(E-V_0)}{{\hslash }^2}}\end{array}}$

q₁ es real y q₂ es imaginario. E<V₀ es la energía de un nivel, si la solución de le ecuación de Schrödinger, Ψ(x) tiende asintóticamente a cero para grandes valores de x.

${\displaystyle \underset{x\to \pm \infty }{\lim }\Psi (x)=0}$

Ψ₂(x) debe tender a cero cuando x se hace grande, para ello B₂ tiene que ser cero.

Las condiciones de continuidad de la función de onda Ψ(x) y su derivada primera en la frontera x=a entre las dos regiones de distinto potencial, constituyen un par de ecuaciones que relacionan A₁ y B₁ con A₂.

${\displaystyle \begin{array}{l}x=a\{\begin{array}{l}{A}_1\exp \left(i{q}_{1}a\right)+B_1\exp \left(-i{q}_{1}a\right)=A_2\exp \left(i{q}_{2}a\right)\\ q_1{A}_1\exp \left(i{q}_{1}a\right)-q_1{B}_1\exp \left(-i{q}_{1}a\right)=q_2{A}_2\exp \left(i{q}_{2}a\right)\end{array}\\ A_1=\frac{q_1+q_2}{2q_1}{A}_2\exp \left(i{q}_{2}a\right)\exp \left(-i{q}_{1}a\right)\\ B_1=\frac{q_1-q_2}{2q_1}{A}_2\exp \left(i{q}_{2}a\right)\exp \left(i{q}_{1}a\right)\end{array}}$

Este último parámetro, determina la escala vertical de la función de onda Ψ(x), y se puede obtener a partir de la condición de normalización

${\displaystyle {\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{\left|\Psi (x)\right|}^{2}dx=1}}$

Niveles de energía

La simetría de la función potencial E_p(x) hace que las funciones de onda sean:

• Simétricos si Ψ(x)=Ψ(-x) o bien, A₁=B₁.

${\displaystyle \left(q_1+q_2\right)\exp \left(-i{q}_{1}a\right)=\left(q_1-q_2\right)\exp \left(i{q}_{1}a\right)}$

Llamando q₁=q y q₂=ik, obtenemos la ecuación transcendente

q·sin(qa)-k·cos(qa)=0

• Antisimétricos si Ψ(x)=-Ψ(-x) o bien, A₁=-B₁.

Los niveles de energía para los estados antisimétricos se obtienen haciendo que Ψ(x)=-Ψ(-x)

${\displaystyle \left(q_1+q_2\right)\exp \left(-i{q}_{1}a\right)=-\left(q_1-q_2\right)\exp \left(i{q}_{1}a\right)}$

k·sin(qa)+q·cos(qa)=0

Las raíces de las dos ecuaciones nos dan los niveles de energía de la partícula en el pozo de potencial.

Establecemos un sistema de unidades en el que ℏ=m=1. La anchura del potencial es 2a=2·2, la altura V₀=5

function pozo
    a=2;   %la anchura del pozo de potencial es 2a
    V0=5;  %altura del pozo de potencial 
    f=@(E) sqrt(2*(V0-E)).*cos(sqrt(2*E)*a)-sqrt(2*E).*sin(sqrt(2*E)*a); %par
    g=@(E) sqrt(2*E).*cos(sqrt(2*E)*a)+sqrt(2*(V0-E)).*sin(sqrt(2*E)*a); %impar
    xx=linspace(0,V0-0.5,10);
    impar=raices(g,xx);
    par=raices(f,xx);
    disp(par)
    disp(impar)
    
     
    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for m=1:length(indices)
            r(m)=fzero(f, [x(indices(m)), x(indices(m)+1)]);
        end
    end
end

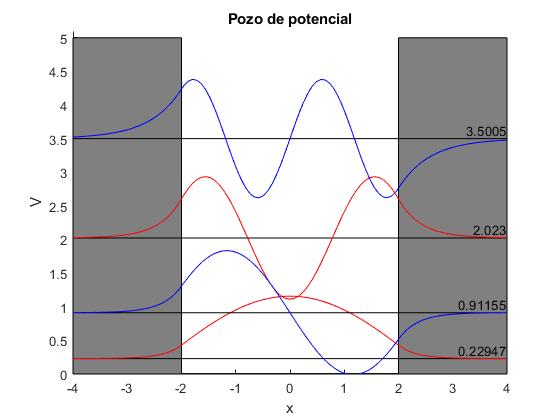
0.2295    2.0230
0.9116    3.5005

La función raices calcula las raíces de las ecuaciones transcendentes empleando a función fzero de MATLAB.

Funciones de onda

Representamos las funciones de onda para cada uno de los niveles de energía

${\displaystyle \begin{array}{l}{\Psi }_1\left(x\right)=A_1\exp \left(i{q}_{1}x\right)+B_1\exp \left(-i{q}_{1}x\right)\\ {\Psi }_2\left(x\right)=A_2\exp \left(i{q}_{2}x\right)\end{array}}$

Subtituyendo q₁=q y q₂=ik

La función de onda simétrica, A₁=B₁ es

${\displaystyle \begin{array}{l}{\Psi }_1\left(x\right)=2A_1\cos \left(qx\right)0\le x\le a\\ {\Psi }_2\left(x\right)=A_2\exp \left(-kx\right)x>a\end{array}}$

La continuidad en x=a establece las relaciones entre A₁ con A₂ que actúa como factor de escala

${\displaystyle A_1=A_2\frac{q\cos (qa)+k\sin (qa)}{2q}\exp (-ka)}$

La función de onda antisimétrica, A₁=-B₁ es

${\displaystyle \begin{array}{l}{\Psi }_1\left(x\right)=2i{A}_1\sin \left(qx\right)0\le x\le a\\ {\Psi }_2\left(x\right)=A_2\exp \left(-kx\right)x>a\\ A_1=i{A}_2\frac{k\cos (qa)-q\sin (qa)}{2q}\exp (-ka)\end{array}}$

Determinamos el valor de A₂ para que la integral

${\displaystyle \begin{array}{l}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\left|\Psi (x)\right|}^2}dx=1\\ {\displaystyle \underset{0}{\overset{\infty }{\int }}{\left|\Psi (x)\right|}^2}dx={\displaystyle \underset{0}{\overset{a}{\int }}{\left|{\Psi }_1(x)\right|}^2}dx+{\displaystyle \underset{a}{\overset{\infty }{\int }}{\left|{\Psi }_2(x)\right|}^2}dx=\frac{1}{2}\\ {\displaystyle \underset{0}{\overset{a}{\int }}4A_1^2{\cos }^2(qx)dx+{\displaystyle \underset{a}{\overset{\infty }{\int }}{A}_2^2\exp (-2kx)dx=2A_1^2\left(a+\frac{\sin (2qa)}{2q}\right)}}+\frac{A_2^2}{2k}\exp (-2ka)\\ {\displaystyle \underset{0}{\overset{a}{\int }}4A_1^2{\sin }^2(qx)dx+{\displaystyle \underset{a}{\overset{\infty }{\int }}{A}_2^2\exp (-2kx)dx=2A_1^2\left(a-\frac{\sin (2qa)}{2q}\right)}}+\frac{A_2^2}{2k}\exp (-2ka)\end{array}}$

Completamos el script anterior, representando el potencial V(x), los tres niveles de energía y las correspondientes funciones de onda, simétricas (color rojo), antisimétricas (azul)

function pozo_1
    a=2;   %la anchura del pozo de potencial es 2a
    V0=5;  %altura del pozo de potencial 
    f=@(E) sqrt(2*(V0-E)).*cos(sqrt(2*E)*a)-sqrt(2*E).*sin(sqrt(2*E)*a); %par
    g=@(E) sqrt(2*E).*cos(sqrt(2*E)*a)+sqrt(2*(V0-E)).*sin(sqrt(2*E)*a); %impar
    xx=linspace(0,V0-0.5,10);
    impar=raices(g,xx);
    par=raices(f,xx);
    disp(par)
    disp(impar)
    
    hold on
    %pozo de potencial
    xx=[-4 -4 -a -a a a 4 4];
    yy=[0 V0 V0 0 0 V0 V0 0];
    fill(xx,yy, [0.5 0.5 0.5])
    %niveles de nergía y funciones de onda
    for i=1:length(par)
       %nivel de energía
        line([-4 4],[par(i) par(i)], 'color','k')
        text(4, par(i),num2str(par(i)),'VerticalAlignment','bottom', 
'HorizontalAlignment','right');

        %función de onda (simétrica)
        q=sqrt(2*par(i));
        k=sqrt(2*(V0-par(i)));
        A1=(q*cos(q*a)+k*sin(q*a))*exp(-k*a)/(2*q);
        suma=2*A1^2*a+A1^2*sin(2*q*a)/q+exp(-2*k*a)/(2*k);
        x=linspace(0,4,50);
        y=((2*A1*cos(q*x)).*(x<=a)+(exp(-k*x)).*(x>a))/sqrt(suma);
        plot([fliplr(-x) x], [par(i)+fliplr(y) par(i)+y],'r');
    end
    for i=1:length(impar)
       %nivel de energía
        line([-4 4],[impar(i) impar(i)], 'color','k')
        text(4, impar(i),num2str(impar(i)), 'VerticalAlignment','bottom',
 'HorizontalAlignment','right');
        %función de onda (antisimétrica)
        q=sqrt(2*impar(i));
        k=sqrt(2*(V0-impar(i)));
        A1=(k*cos(q*a)-q*sin(q*a))*exp(-k*a)/(2*q);
        suma=2*A1^2*a-A1^2*sin(2*q*a)/q+exp(-2*k*a)/(2*k);
        x=linspace(0,4,50);
        y=((2*A1*sin(q*x)).*(x<=a)-(exp(-k*x)).*(x>a))/sqrt(suma);
        plot([fliplr(-x) x], [impar(i)+fliplr(-y) impar(i)+y],'b');
    end
    ylim([0 V0+0.1]);

    hold off
    xlabel('x');
    ylabel('V')
    title('Pozo de potencial')
     
    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for m=1:length(indices)
            r(m)=fzero(f, [x(indices(m)), x(indices(m)+1)]);
        end
    end
end

Pozo de potencial de forma triangular

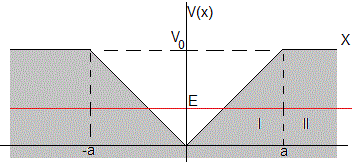
En este apartado, resolveremos la ecuación de Schrödinger unidimensional e independiente del tiempo en el potencial

${\displaystyle V(x)=\{\begin{array}{l}{V}_0,x<-a\\ -V_0\frac{x}{a},-a\le x<0\\ V_0\frac{x}{a},0\le x\le a\\ V_0,x>a\end{array}}$

Para un potencial simétrico, resolveremos la ecuación de Schrödinger para E<V₀ en las regiones I y II

${\displaystyle \begin{array}{l}\frac{d^2{\psi }_I(x)}{d{x}^2}-\frac{2m}{{\hslash }^2}\left(V_0\frac{x}{a}-E\right){\psi }_I(x)=\mathrm{0,}0\le x\le a\\ \frac{d^2{\psi }_{II}(x)}{d{x}^2}-\frac{2m}{{\hslash }^2}\left(V_0-E\right)·{\psi }_{II}(x)=\mathrm{0,}x>a\end{array}}$

La solución de la segunda, en la región II es

${\displaystyle {\psi }_{II}(x)=C\exp \left(-kx\right)+D\exp \left(kx\right),k^2=\frac{2m}{{\hslash }^2}\left(V_0-E\right)}$

El coeficiente D deberá ser nulo para evitar que la función de onda se haga muy grande cuando x→∞.

En la región I, hacemos el cambio de variable z=αx+β, dz=α·dx, de modo que la ecuación diferencial se transforme

${\displaystyle \begin{array}{l}\frac{d^2{\psi }_I(z)}{d{z}^2}-z·{\psi }_I(z)=\mathrm{0,}{\psi }_I(z)=A·\text{Ai}(z)\text{+}B·\text{Bi}(z)\\ z={\left(\frac{2m}{{\hslash }^2}{V}_0{a}^2\right)}^{1/3}\left(\frac{x}{a}-\frac{E}{V_0}\right)=r\left(\frac{x}{a}-\frac{E}{V_0}\right)\end{array}}$

cuya solución es una combinación lineal de las funciones de Airy, Ai(x) y Bi(x).

Las posiciones x=0 y x=a, corresponden a los valores de la variable z

${\displaystyle \begin{array}{l}{z}_0=-r\frac{E}{V_0}\\ z_a=r\left(1-\frac{E}{V_0}\right)\end{array}}$

Continuidad

La función de onda y su derivada primera son continuas en x=a.

${\displaystyle \begin{array}{l}{\psi }_I(z_a)={\psi }_{II}(a)\\ {\frac{d{\psi }_I(x)}{dx}|}_{x=a}={\frac{d{\psi }_{II}(x)}{dx}|}_{x=a}\end{array}}$

La segunda condición (continuidad de la derivada primera) se expresa en términos de la variable z

${\displaystyle \begin{array}{l}\frac{d{\psi }_I(x)}{dx}=\frac{d{\psi }_I(z)}{dz}\frac{dz}{dx}=\frac{r}{a}\frac{d{\psi }_I(z)}{dz}\\ {\frac{r}{a}{\frac{d{\psi }_I(z)}{dz}|}_{z=z_a}=\frac{d{\psi }_{II}(x)}{dx}|}_{x=a}\end{array}}$

La continuidad en x=a, es

${\displaystyle x=a\{\begin{array}{l}A·\text{Ai}(z_a)\text{+}B·\text{Bi}(z_a)=C\exp (-ka)\\ r\left(A·\text{Ai'}(z_a)\text{+}B·\text{Bi'}(z_a)\right)=-kaC\exp (-ka)\end{array}}$

El símbolo ' significa la derivada de las función de Airy Ai(z) o Bi(z) respecto de la variable z. Esta derivada se evalúa en z=z_a

Niveles de energía

• Funciones de onda antisimétricas

Se anulan en el origen

${\displaystyle \begin{array}{l}{\psi }_I(z_0)=0\\ A·\text{Ai}(z_0)\text{+}B·\text{Bi}(z_0)=0\end{array}}$

Con las dos ecuaciones de continuidad en x=a, tenemos un sistema homogéneo de tres ecuaciones con tres incógnitas. Obtenemos una ecuación transcentente de la energía E, cuyas raíces nos proporconan el valor de la energía de los niveles

${\displaystyle \text{Bi}(z_0)\left\{\left(ka\right)\text{Ai}(z_a)+r\text{Ai'}(z_a)\right\}-\text{Ai}(z_0)\left\{\left(ka\right)\text{Bi}(z_a)+r\text{Bi'}(z_a)\right\}=0}$

• Funciones de onda simétricas

La derivada (pendiente) se anulan en el origen

${\displaystyle \begin{array}{l}{\frac{d{\psi }_I(x)}{dx}|}_{x=0}=0\\ \frac{r}{a}{\frac{d{\psi }_I(z)}{dz}|}_{z=z_0}=0\\ A·\text{Ai'}(z_0)\text{+}B·\text{Bi'}(z_0)=0\end{array}}$

Con las dos ecuaciones de continuidad en x=a, tenemos un sistema homogéneo de tres ecuaciones con tres incógnitas. Obtenemos una ecuación transcentente de la energía E, cuyas raíces nos proporconan el valor de la energía de los niveles

${\displaystyle \text{Bi'}(z_0)\left\{\left(ka\right)\text{Ai}(z_a)+r\text{Ai'}(z_a)\right\}-\text{Ai'}(z_0)\left\{\left(ka\right)\text{Bi}(z_a)+r\text{Bi'}(z_a)\right\}=0}$

Establecemos un sistema de unidades en el que ℏ=m=1. La anchura del potencial es 2a=2·2, la altura V₀=5

function airy_7
    a=2; %la anchura del pozo es 2a
    V0=5; %profundidad
    rr=(2*V0*a^2)^(1/3); %constante
    xx=linspace(0,V0-0.1,10);
    rI=raices(@fImpar,xx);
    rP=raices(@fPar,xx);
    En=sort([rI,rP]);
    disp(En)

    function res=fImpar(E)    
        z0=-rr*E/V0;
        za=rr*(1-E/V0);
        k=sqrt(2*(V0-E));
        res=(a*k.*airy(0,za)+rr*airy(1,za)).*airy(2,z0)-airy(0,z0).*
(a*k.*airy(2,za)+rr*airy(3,za));
    end

    function res=fPar(E)    
        z0=-rr*E/V0;
        za=rr*(1-E/V0);
        k=sqrt(2*(V0-E));
        res=(a*k.*airy(0,za)+rr*airy(1,za)).*airy(3,z0)-airy(1,z0).*
(a*k.*airy(2,za)+rr*airy(3,za));
    end
    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for m=1:length(indices)
            r(m)=fzero(f, [x(indices(m)), x(indices(m)+1)]);
        end
    end
end

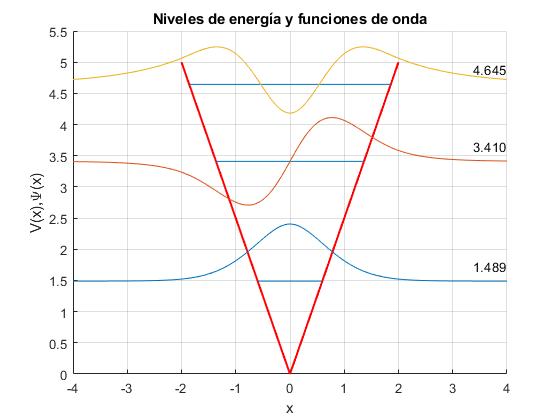
1.4893    3.4103    4.6449

Funciones de onda

${\displaystyle \{\begin{array}{l}{\psi }_I(x)=A·\text{Ai}(z)\text{+}B·\text{Bi}(z),0\le x<a,z=r\left(\frac{x}{a}-\frac{E}{V_0}\right)\\ {\psi }_{II}(z)=C\exp (-kx),a\le x<\infty \end{array}}$

Los coeficientes B y C están relacionados con A. El coeficiente A se calcula de modo que

${\displaystyle {\displaystyle \underset{0}{\overset{a}{\int }}{\left|{\psi }_I(x)\right|}^{2}dx+}{\displaystyle \underset{a}{\overset{\infty }{\int }}{\left|{\psi }_{II}(x)\right|}^{2}dx=\frac{1}{2}}}$

por la simetría de la función de onda. La segunda integral es inmediata. La primera integral se resuelve numéricamente utilizando integral de MATLAB para ello se hace el cambio de variable de x a z, dz=(r/a)·dx, los nuevo límites de integración son z₀ y z_a

${\displaystyle \frac{a}{r}{\displaystyle \underset{z_0}{\overset{z_a}{\int }}{\left(A·\text{Ai}(z)\text{+}B·\text{Bi}(z)\right)}^{2}dz+}\frac{1}{2k}\exp (-2ka)=\frac{1}{2}}$

• Funciones de onda antisimétricas

${\displaystyle \begin{array}{l}B=-\frac{\text{Ai}(z_0)}{\text{Bi}(z_0)}A\\ C=A\left(\text{Ai}(z_a)-\frac{\text{Ai}(z_0)}{\text{Bi}(z_0)}·\text{Bi}(z_a)\right)\exp (ka)\end{array}}$

• Funciones de onda simétricas

${\displaystyle \begin{array}{l}B=-\frac{\text{Ai'}(z_0)}{\text{Bi'}(z_0)}A\\ C=A\left(\text{Ai}(z_a)-\frac{\text{Ai'}(z_0)}{\text{Bi'}(z_0)}·\text{Bi}(z_a)\right)\exp (ka)\end{array}}$

Completamos el script anterior, representando el potencial V(x), los tres niveles de energía y las correspondientes funciones de onda, simétrica y antisimétrica

function airy_8
    a=2; %anchura 2a
    V0=5; %profundidad
    rr=(2*V0*a^2)^(1/3); %constante
    xx=linspace(0,V0-0.1,10);
    rI=raices(@fImpar,xx);
    rP=raices(@fPar,xx);
    En=sort([rI,rP]);
    disp(En)
    hold on
    %potencial V(x)
    line([-a,0],[V0,0], 'color','r', 'lineWidth',1.5)
    line([0,a],[0,V0], 'color','r', 'lineWidth',1.5)
%niveles de energíafunciones de onda
    x=linspace(0,2*a,100);
    for m=1:length(En)
        z0=-rr*En(m)/V0;
        za=rr*(1-En(m)/V0);
        k=sqrt(2*(V0-En(m)));
        if rem(m,2)==1 %si es par m=1,3,5...
             line([-En(m)*a/V0,En(m)*a/V0],[En(m),En(m)]) %nivel de energía
             B=-airy(1,z0)/airy(3,z0);
             C=exp(k*a)*(airy(0,za)+B*airy(2,za));
             f=@(z) airy(0,z)+B*airy(2,z);
             g=@(z) f(z).^2;
             A=sqrt(0.5/(a*integral(g,z0,za)/rr+C^2*exp(-2*k*a)/(2*k)));
             y=A*((x<=a).*f(rr*(x/a-En(m)/V0))+C*(x>a).*exp(-k*x));
             yy=[fliplr(y)+En(m),y+En(m)];
        else %si es impar m=2,4,6...
            line([-En(m)*a/V0,En(m)*a/V0],[En(m),En(m)]) %nivel de energía
            B=-airy(0,z0)/airy(2,z0);
            C=exp(k*a)*(airy(0,za)+B*airy(2,za));
            f=@(z) airy(0,z)+B*airy(2,z);
             g=@(z) f(z).^2;
             A=sqrt(0.5/(a*integral(g,z0,za)/rr+C^2*exp(-2*k*a)/(2*k)));
             y=A*((x<=a).*f(rr*(x/a-En(m)/V0))+C*(x>a).*exp(-k*x));
             yy=[-fliplr(y)+En(m),y+En(m)];
        end 
        plot([-fliplr(x),x],yy)
        text(4,En(m)+0.1,sprintf('%1.3f',En(m)),'VerticalAlignment','bottom', 
'HorizontalAlignment','right')
    end
    hold off
    ylim([0,V0])
    grid on
    xlabel('x')
    ylabel('V(x),\Psi(x)')
    title('Niveles de energía y funciones de onda')

    function res=fImpar(E)    
        z0=-rr*E/V0;
        za=rr*(1-E/V0);
        k=sqrt(2*(V0-E));
        res=(a*k.*airy(0,za)+rr*airy(1,za)).*airy(2,z0)-airy(0,z0).
*(a*k.*airy(2,za)+rr*airy(3,za));
    end
    function res=fPar(E)    
        z0=-rr*E/V0;
        za=rr*(1-E/V0);
        k=sqrt(2*(V0-E));
        res=(a*k.*airy(0,za)+rr*airy(1,za)).*airy(3,z0)-airy(1,z0).
*(a*k.*airy(2,za)+rr*airy(3,za));
    end

    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for m=1:length(indices)
            r(m)=fzero(f, [x(indices(m)), x(indices(m)+1)]);
        end
    end
end