Otros pozos rectangulares de potencial

Pozo de potencial asimétrico (I)

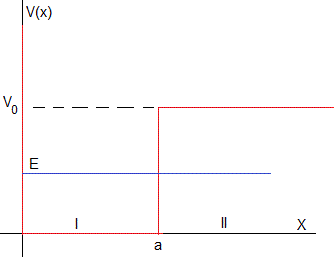
Consideremos un pozo de potencial rectangular de anchura a y profundidad V₀, descrito por la función V(x)

$V (x) = {\begin{cases} \infty, x \leq 0 \\ 0, 0 < x \leq a \\ V_{0}, x > a \end{cases}$

Estudiamos la solución de la la ecuación de Schrödinger independiente del tiempo para energías E<V₀

$- \frac{ℏ^{2}}{2 m} \frac{d^{2} ψ (x)}{d x^{2}} + V (x) \cdot ψ (x) = E \cdot ψ (x)$

En la región I

$\begin{array}{l} \frac{d^{2} ψ (x)}{d x^{2}} + \frac{2 m}{ℏ^{2}} E \cdot ψ (x) = 0, k^{2} = \frac{2 m}{ℏ^{2}} E \\ ψ_{I} (x) = A e^{i k x} + B e^{- i k x} \end{array}$

En x=0, el potencial es infinito, por lo que

$ψ_{I} (0) = A + B = 0$

En la región II

$\begin{array}{l} - \frac{ℏ^{2}}{2 m} \frac{d^{2} ψ (x)}{d x^{2}} + V_{0} \cdot ψ (x) = E \cdot ψ (x) \\ \frac{d^{2} ψ (x)}{d x^{2}} - \frac{2 m}{ℏ^{2}} (V_{0} - E) ψ (x) = 0, q^{2} = \frac{2 m}{ℏ^{2}} (V_{0} - E), E < V_{0} \\ ψ_{I I} (x) = C e^{q x} + D e^{- q x} \end{array}$

Cuando x→∞ el primer término se hace muy grande, por lo que el coeficiente D deberá anularse, D=0

La función de onda en las regiones I y II es

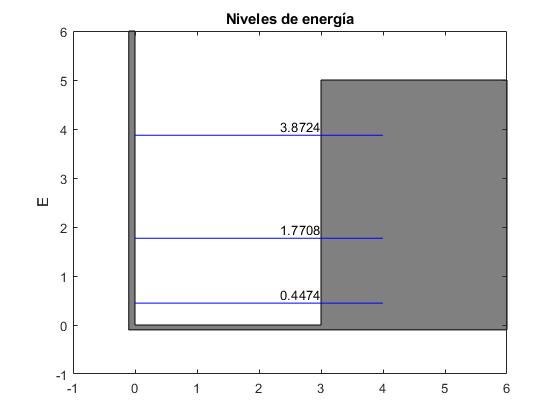
${\begin{cases} ψ_{I} (x) = A e^{i k x} - A e^{- i k x} \\ ψ_{I I} (x) = D e^{- q x} \end{cases}$

Niveles de energía

La función de onda y su derivada primera es continua en x=a

$\begin{array}{l} {\begin{cases} ψ_{I} (a) = ψ_{I I} (a) \\ {\frac{d ψ_{I} (x)}{d x} |}_{x = a} = {\frac{d ψ_{I I} (x)}{d x} |}_{x = a} \end{cases} \\ {\begin{cases} A e^{i k a} - A e^{- i k a} = D e^{- q a} \\ i k (A e^{i k a} + A e^{- i k a}) = - q D e^{- q a} \end{cases} \end{array}$

Eliminando A y D de este sistema homogéneo, obtenemos una la ecuación transcendente que determina los niveles de energía permitidos

$q \sin (k a) + k \cos (k a) = 0$

Establecemos un sistema de unidades tal que ℏ=m=1. La ecuación transcendente se escribe en términos de la energía E

$\sqrt{2 V_{0} - 2 E} \sin (a \sqrt{2 E}) + \sqrt{2 E} \cos (a \sqrt{2 E}) = 0$

La altura del pozo rectangular asimétrico es V₀=5 y la anchura a=3. Utilizamos la función raices para obtener las raíces de la ecuación transcendente. Representamos la función potencial V(x) y los niveles de energía

function semi_1
    V0=5; %altura
    a=3; %anchura
    f=@(E) sqrt(2*V0-2*E).*sin(sqrt(2*E)*a)+sqrt(2*E).*cos(sqrt(2*E)*a);
    x=linspace(0,V0, 20);
    rr=raices(f,x);
    disp(rr)
    %potencial
    xx=[-0.1, 0, 0, a, a, 2*a, 2*a, -0.1, -0.1];
    yy=[V0+1, V0+1, 0, 0, V0, V0, -0.1, -0.1, V0+1];
    fill(xx,yy, [0.5 0.5 0.5])
    %niveles de energía
    for E=rr
        line([0,a+1],[E,E],'color','b')
        text(a, E,num2str(E),'VerticalAlignment','bottom', 'HorizontalAlignment'
,'right')
   end
    xlabel('')
    ylabel('E')
    title('Niveles de energía')

    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

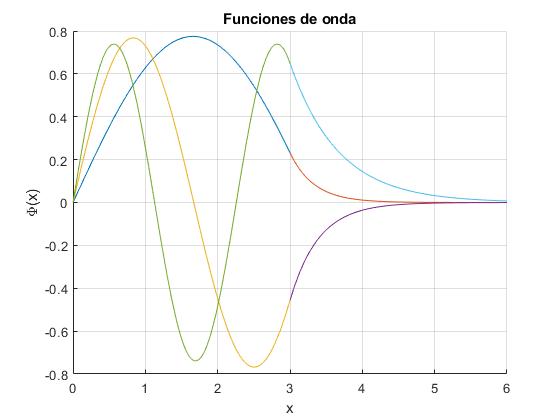
Funciones de onda

La continuidad de la función de onda en x=a relaciona los coeficientes D y A

$D = 2 A i \sin (k a) e^{q a}$

La función de onda en las regiones I y II es

${\begin{cases} ψ_{I} (x) = A e^{i k x} - A e^{- i k x} = 2 A i \sin (k x), 0 \leq x < a \\ ψ_{I I} (x) = D e^{- q x} = 2 A i \sin (k a) e^{q a} \exp (- q x), a \leq x < \infty \end{cases}$

El coeficiente A se calcula de modo que

$\begin{array}{l} \int_{0}^{a} ψ_{I} (x) ψ_{I}^{*} (x) d x + \int_{a}^{\infty} ψ_{I I} (x) ψ_{I I}^{*} (x) d x = 1 \\ 4 A^{2} \int_{0}^{a} \sin^{2} (k x) d x + 4 A^{2} \sin^{2} (k a) \int_{a}^{\infty} \exp (- 2 q x) d x = 1 \\ 2 (a - \frac{\sin (2 k a)}{2 k} + \frac{\sin^{2} (k a)}{q}) A^{2} = 1 \end{array}$

Representamos las funciones de onda correspondientes a los tres niveles de energía

function semi
    V0=5; %altura
    a=3; %anchura
    %niveles de energía
    f=@(E) sqrt(2*V0-2*E).*sin(sqrt(2*E)*a)+sqrt(2*E).*cos(sqrt(2*E)*a);
    x=linspace(0,V0, 20);
    rr=raices(f,x);
    %funciones de onda
    hold on
    for E=rr
       q=sqrt(2*V0-2*E);
       k=sqrt(2*E);
       A=1/sqrt(2*(a-sin(2*k*a)/(2*k)+sin(k*a)^2/q));
       f1=@(x) 2*A*sin(k*x);
       f2=@(x) 2*A*sin(k*a)*exp(q*a)*exp(-q*x);
       fplot(f1,[0,a])
       fplot(f2,[a,2*a])
    end
    hold off
    grid on
    xlabel('x')
    ylabel('\Phi(x)')
    title('Funciones de onda')

    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

Pozo de potencial asimétrico (II)

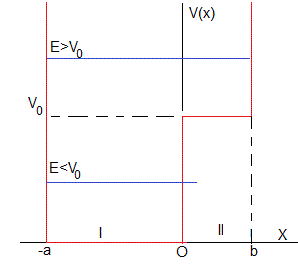
Consideremos un pozo de potencial de altura infinita

$V (x) = {\begin{cases} \infty, x \leq - a \\ 0, - a < x \leq 0 \\ V_{0}, 0 < x \leq b \\ \infty, x > b \end{cases}$

Estudiamos las soluciones de la la ecuación de Schrödinger independiente del tiempo

$- \frac{ℏ^{2}}{2 m} \frac{d^{2} ψ (x)}{d x^{2}} + V (x) \cdot ψ (x) = E \cdot ψ (x)$

primero para E<V₀ y a continuación, para E>V₀

Energía, E<V₀

En la región I

$\begin{array}{l} \frac{\partial^{2} ψ (x)}{\partial x^{2}} + \frac{2 m}{ℏ^{2}} E \cdot ψ (x) = 0, k^{2} = \frac{2 m}{ℏ^{2}} E \\ ψ_{I} (x) = A e^{i k x} + B e^{- i k x} \end{array}$

En la región II

$\begin{array}{l} - \frac{ℏ^{2}}{2 m} \frac{\partial^{2} ψ (x)}{\partial x^{2}} + V_{0} \cdot ψ (x) = E \cdot ψ (x) \\ \frac{\partial^{2} ψ (x)}{\partial x^{2}} - \frac{2 m}{ℏ^{2}} (V_{0} - E) ψ (x) = 0, q^{2} = \frac{2 m}{ℏ^{2}} (V_{0} - E), E < V_{0} \\ ψ_{I I} (x) = C e^{q x} + D e^{- q x} \end{array}$

Niveles de energía

En x=-a, el potencial es infinito

$ψ_{I} (- a) = A e^{- i k a} + B e^{i k a} = 0$

En x=b, el potencial es infinito

$ψ_{I I} (b) = C e^{q b} + D e^{- q b} = 0$

La función de la función de onda y su derivada primera son continuas en x=0

$\begin{array}{l} {\begin{cases} ψ_{I} (0) = ψ_{I I} (0) \\ {\frac{d ψ_{I} (x)}{d x} |}_{x = 0} = {\frac{d ψ_{I I} (x)}{d x} |}_{x = 0} \end{cases} \\ {\begin{cases} A + B = C + D \\ i k (A - B) = q (C - D) \end{cases} \end{array}$

Tenemos un sistema homogéneeo de cuatro ecuaciones con cuatro incógnitas

${\begin{cases} A e^{- i k a} + B e^{i k a} = 0 \\ C e^{q b} + D e^{- q b} = 0 \\ A + B = C + D \\ i k (A - B) = q (C - D) \end{cases}$

El determinante de los coeficientes es cero

$| \begin{matrix} e^{- i k a} & e^{i k a} & 0 & 0 \\ 0 & 0 & e^{q b} & e^{- q b} \\ 1 & 1 & - 1 & - 1 \\ i k & - i k & - q & q \end{matrix} | = 0$

Después de un largo proceso de simplificación, obtenemos la ecuación transcendente

$\exp (q b) (k \cos (k a) + q \sin (k a)) + \exp (- q b) (- k \cos (k a) + q \sin (k a)) = 0$

Energía, E>V₀

En la región I

La misma solución

$ψ_{I} (x) = A e^{i k x} + B e^{- i k x}, k^{2} = \frac{2 m}{ℏ^{2}} E$

En la región II

$\begin{array}{l} q^{2} = \frac{2 m}{ℏ^{2}} (E - V_{0}), E > V_{0} \\ ψ_{I I} (x) = C e^{i q x} + D e^{- i q x} \end{array}$

Niveles de energía

En x=-a, el potencial es infinito

$ψ_{I} (- a) = A e^{- i k a} + B e^{i k a} = 0$

En x=b, el potencial es infinito

$ψ_{I I} (b) = C e^{i q b} + D e^{- i q b} = 0$

La función de la función de onda y su derivada primera son continuas en x=0

$\begin{array}{l} {\begin{cases} ψ_{I} (0) = ψ_{I I} (0) \\ {\frac{d ψ_{I} (x)}{d x} |}_{x = 0} = {\frac{d ψ_{I I} (x)}{d x} |}_{x = 0} \end{cases} \\ {\begin{cases} A + B = C + D \\ k (A - B) = q (C - D) \end{cases} \end{array}$

Tenemos un sistema homogéneeo de cuatro ecuaciones con cuatro incógnitas

${\begin{cases} A e^{- i k a} + B e^{i k a} = 0 \\ C e^{i q b} + D e^{- i q b} = 0 \\ A + B = C + D \\ k (A - B) = q (C - D) \end{cases}$

El determinante de los coeficientes es cero

$| \begin{matrix} e^{- i k a} & e^{i k a} & 0 & 0 \\ 0 & 0 & e^{i q b} & e^{- i q b} \\ 1 & 1 & - 1 & - 1 \\ k & - k & - q & q \end{matrix} | = 0$

Después de un largo proceso de simplificación, obtenemos la ecuación transcendente

$q \sin (k a) \cos (q b) + k \cos (k a) \sin (q b) = 0$

Establecemos un sistema de unidades tal que ℏ=m=1.

Representamos la función potencial V(x) y los niveles de energía para a=b=3 y V₀=20.

function caja_asimetrica
    V0=20; %altura
    a=3; %dimesiones
    b=3;
    q=@(E) sqrt(V0-E);
    k=@(E) sqrt(E);
    f=@(E) exp(q(E)*b).*(k(E).*cos(k(E)*a)+q(E).*sin(k(E)*a))+
exp(-q(E)*b).*(-k(E).*cos(k(E)*a)+q(E).*sin(k(E)*a));
    x=linspace(0,V0, 50);
    r1=raices(f,x);
    disp(r1)
    q=@(E) sqrt(E-V0);
    f=@(E) q(E).*(sin(k(E)*a).*cos(q(E)*b))+k(E).*(sin(q(E)*b).*cos(k(E)*a));
    x=linspace(V0, 30,20);
    r2=raices(f,x);
    disp(r2)
    %potencial
    xx=[-0.1-a,-0.1-a, -a, -a, 0, 0, b, b, b+0.1, b+0.1];
    yy=[-0.1, V0+10, V0+10, 0, 0, V0, V0, V0+10, V0+10,-0.1];
    fill(xx,yy, [0.5 0.5 0.5])
    ylim([-0.1,V0+10])
    %niveles de energía
    for E=r1
        line([-a,1],[E,E],'color','b')
        text(-a-0.3, E,sprintf('%1.3f',E),'VerticalAlignment','bottom', 
'HorizontalAlignment','right')
   end
    for E=r2
        line([-a,b],[E,E],'color','b')
        text(-a-0.3, E,sprintf('%1.3f',E),'VerticalAlignment','bottom', 
'HorizontalAlignment','right')
    end
    axis off
    xlabel('')
    ylabel('E')
    title('Niveles de energía')

    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for s=1:length(indices)
            r(s)=fzero(f, [x(indices(s)), x(indices(s)+1)]);
        end
    end
end

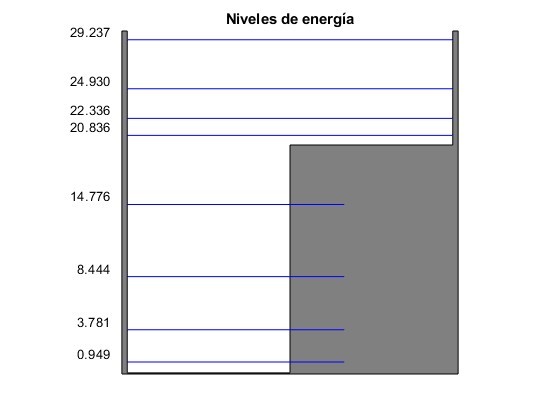
    0.9487    3.7809    8.4439   14.7763
   20.8357   22.3363   24.9302   29.2372

Funciones de onda

Vamos a representar las funciones de onda correspondientes a los niveles de energía en cada uno de los dos casos, E<V₀ y E>V₀. Para ello, tenemos que relacionar los coeficientes B, C y D con el coeficiente A. El coeficiente A se calcula de modo que

$\int_{- a}^{0} ψ_{I} (x) ψ_{I}^{*} (x) d x + \int_{0}^{b} ψ_{I I} (x) ψ_{I I}^{*} (x) d x = 1$

Correspondientes a los niveles de energía, E<V₀

${\begin{cases} ψ_{I} (x) = A e^{i k x} + B e^{- i k x} \\ ψ_{I I} (x) = C e^{q x} + D e^{- q x} \end{cases}$

Calculamos la integral

$\begin{array}{l} \int_{- a}^{0} (A A^{*} + B B^{*} + A B^{*} \exp (2 i k x) + B A^{*} \exp (- 2 i k x)) d x + \int_{0}^{b} (C C^{*} \exp (2 q x) + D D^{*} \exp (- 2 q x) + C D^{*} + D C^{*}) d x = 1 \\ (A A^{*} + B B^{*}) a + \frac{A B^{*}}{2 i k} (1 - e^{- 2 i k a}) - \frac{B A^{*}}{2 i k} (1 - e^{2 i k a}) + (C D^{*} + D C^{*}) b + \frac{C C^{*}}{2 q} (e^{2 q b} - 1) - \frac{D D^{*}}{2 q} (e^{- 2 q b} - 1) = 1 \end{array}$

Expresamos los coeficientes B, C y D en términos de A

$\begin{array}{l} {\begin{cases} B = - A e^{- 2 i k a} \\ C = \frac{1 - e^{- 2 i k a}}{1 - e^{2 q b}} \\ D = \frac{1 - e^{- 2 i k a}}{1 - e^{- 2 q b}} \end{cases} \\ A A^{*} + B B^{*} = 2 A^{2}, A B^{*} = - A^{2} e^{2 i k a}, B A^{*} = - A^{2} e^{- 2 i k a} \\ C D^{*} + D C^{*} = 4 \frac{1 - \cos (2 k a)}{(1 - e^{- 2 q b}) (1 - e^{2 q b})}, C C^{*} = 2 \frac{1 - \cos (2 k a)}{{(1 - e^{2 q b})}^{2}}, D D^{*} = 2 \frac{1 - \cos (2 k a)}{{(1 - e^{- 2 q b})}^{2}} \end{array}$

El resultado es

$A^{2} {2 a - \frac{\sin (2 k a)}{k} + (1 - \cos (2 k a)) \frac{4 b q + e^{- 2 q b} - e^{2 q b}}{q (1 - e^{2 q b}) (1 - e^{- 2 q b})}} = 1$

Representamos las funciones de onda correspondientes a los tres primeros niveles de energía, E<V₀

function caja_asimetrica_1
    V0=20; %altura
    a=3; %dimesiones
    b=3;
    q=@(E) sqrt(V0-E);
    k=@(E) sqrt(E);
    f=@(E) exp(q(E)*b).*(k(E).*cos(k(E)*a)+q(E).*sin(k(E)*a))+
exp(-q(E)*b).*(-k(E).*cos(k(E)*a)+q(E).*sin(k(E)*a));
    x=linspace(0,V0, 50);
    r1=raices(f,x);
    hold on
    for E=r1(1:3)
        q=sqrt(V0-E);
        k=sqrt(E);
        A=1/sqrt(2*a-sin(2*k*a)/k+(1-cos(2*k*a)*(4*q*b+exp(-2*b*q*b)-exp(2*q*b))
/(q*(1-exp(2*q*b))*(1-exp(-2*q*b)))));
        B=-A*exp(-2*1i*k*a);
        f1=@(x) real(A*exp(1i*k*x)+B*exp(-1i*k*x));
        fplot(f1,[-a,0])
        C=(1-exp(-2*1i*k*a))*A/(1-exp(2*q*b));
        D=(1-exp(-2*1i*k*a))*A/(1-exp(-2*q*b));
        f2=@(x) real(C*exp(q*x)+D*exp(-q*x));
        fplot(f2,[0,b])  
    end
    hold off
    grid on
    xlabel('x')
    ylabel('\Psi(x)')
    title('Funciones de onda')

    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for s=1:length(indices)
            r(s)=fzero(f, [x(indices(s)), x(indices(s)+1)]);
        end
    end
end

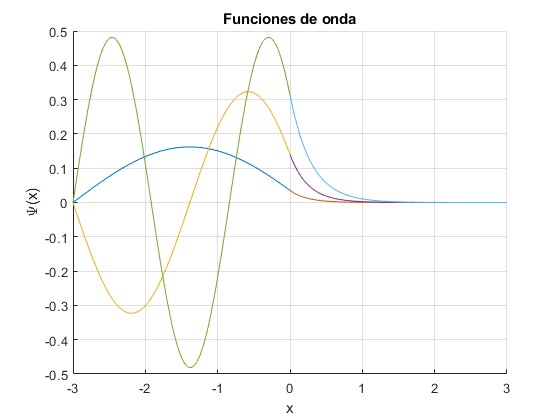
Correspondientes a los niveles de energía, E>V₀

${\begin{cases} ψ_{I} (x) = A e^{i k x} + B e^{- i k x} \\ ψ_{I I} (x) = C e^{i q x} + D e^{- i q x} \end{cases}$

Calculamos la integral

$\begin{array}{l} \int_{- a}^{0} (A A^{*} + B B^{*} + A B^{*} \exp (2 i k x) + B A^{*} \exp (- 2 i k x)) d x + \int_{0}^{b} (C C^{*} + D D^{*} + C D^{*} \exp (2 i k x) + D C^{*} \exp (- 2 i k x)) d x = 1 \\ (A A^{*} + B B^{*}) a + \frac{A B^{*}}{2 i k} (1 - e^{- 2 i k a}) - \frac{B A^{*}}{2 i k} (1 - e^{2 i k a}) + (C C^{*} + D D^{*}) b + \frac{C D^{*}}{2 i k} (e^{2 i k b} - 1) - \frac{D C^{*}}{2 i k} (e^{- 2 i k b} - 1) = 1 \end{array}$

Expresamos los coeficientes B, C y D en términos de A

${\begin{cases} B = - A e^{- 2 i k a} \\ C = \frac{1 - e^{- 2 i k a}}{1 - e^{2 i q b}} \\ D = \frac{1 - e^{- 2 i k a}}{1 - e^{- 2 i q b}} \end{cases}$

El resultado es

$A^{2} {2 a - \frac{\sin (2 k a)}{k} - \frac{1 - \cos (2 k a)}{q (1 - \cos (2 q b))} \sin (2 q b)} = 1$

Representamos las funciones de onda correspondientes a los dos primeros niveles de energía, E>V₀

function caja_asimetrica_2
    V0=20; %altura
    a=3; %dimesiones
    b=3;
    k=@(E) sqrt(E);
    q=@(E) sqrt(E-V0);
    f=@(E) q(E).*(sin(k(E)*a).*cos(q(E)*b))+k(E).*(sin(q(E)*b).*cos(k(E)*a));
    x=linspace(V0, 30,20);
    r2=raices(f,x);
    hold on
    for E=r2(1:2)
        q=sqrt(E-V0);
        k=sqrt(E);
        A=1/sqrt(2*a-sin(2*k*a)/k-(1-cos(2*k*a)*sin(2*q*b)/(q*(1-cos(2*q*b)))));
        B=-A*exp(-2*1i*k*a);
        f1=@(x) real(A*exp(1i*k*x)+B*exp(-1i*k*x));
        fplot(f1,[-a,0])
        C=(1-exp(-2*1i*k*a))*A/(1-exp(2*1i*q*b));
        D=(1-exp(-2*1i*k*a))*A/(1-exp(-2*1i*q*b));
        f2=@(x) real(C*exp(1i*q*x)+D*exp(-1i*q*x));
        fplot(f2,[0,b])  
    end
    hold off
    grid on
    xlabel('x')
    ylabel('\Psi(x)')
    title('Funciones de onda')

    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for s=1:length(indices)
            r(s)=fzero(f, [x(indices(s)), x(indices(s)+1)]);
        end
    end

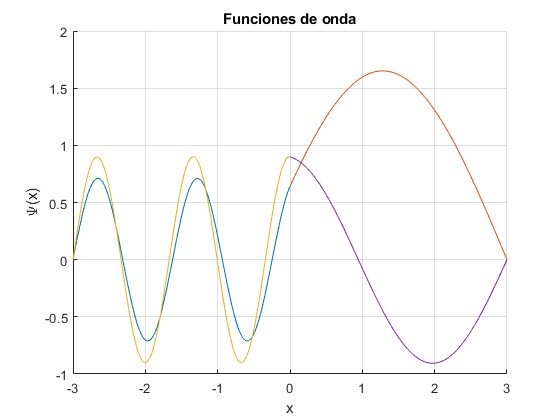
Pozo de potencial doble

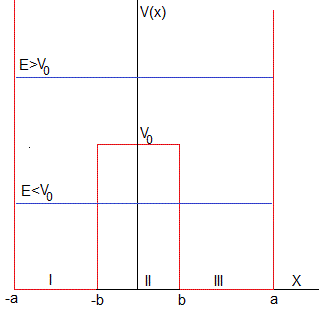
El pozo de potencial doble consta de una pozo de potencial de altura infinita y de anchura 2a con una barrera de potencial de anchura 2b y altura V₀ situada en medio, descrito por la función V(x)

$V (x) = {\begin{cases} \infty, x \leq - a \\ 0, - a < x \leq - b \\ V_{0}, - b < x < b \\ 0, b \leq x < a \\ \infty, x > a \end{cases}$

Estudiamos las soluciones de la la ecuación de Schrödinger independiente del tiempo

$- \frac{ℏ^{2}}{2 m} \frac{d^{2} ψ (x)}{d x^{2}} + V (x) \cdot ψ (x) = E \cdot ψ (x)$

primero para E<V₀ y a continuación, para E>V₀

Energía, E<V₀

En la región I

$\begin{array}{l} \frac{d^{2} ψ (x)}{d x^{2}} + \frac{2 m}{ℏ^{2}} E \cdot ψ (x) = 0, k^{2} = \frac{2 m}{ℏ^{2}} E \\ ψ_{I} (x) = A_{1} e^{i k x} + B_{1} e^{- i k x} \end{array}$

En la región II

En la región III

$\begin{array}{l} \frac{d^{2} ψ (x)}{d x^{2}} + \frac{2 m}{ℏ^{2}} E \cdot ψ (x) = 0, k^{2} = \frac{2 m}{ℏ^{2}} E \\ ψ_{I I I} (x) = A_{2} e^{i k x} + B_{2} e^{- i k x} \end{array}$

Niveles de energía

Las funciones de onda pueden ser

Simétricas

$\begin{array}{l} {\begin{cases} ψ_{I} (- x) = ψ_{I I I} (x) \\ ψ_{I I} (- x) = ψ_{I I} (x) \end{cases} \\ ψ_{I} (x) = A \exp (i k x) + B \exp (- i k x) \\ ψ_{I I} (x) = C \exp (q x) + C \exp (- q x) \\ ψ_{I I I} (x) = B \exp (i k x) + A \exp (- i k x) \end{array}$

En x=a, el potencial es infinito,

$ψ_{I I I} (a) = B \exp (i k a) + A \exp (- i k a) = 0$

La función de onda es continua en x=b y también su derivada primera

$\begin{array}{l} {\begin{cases} B \exp (i k b) + A \exp (- i k b) = C \exp (q b) + C \exp (- q b) \\ i k B \exp (i k b) - i k A \exp (- i k b) = C q \exp (q b) - C q \exp (- q b) \end{cases} \\ {\begin{cases} B (\exp (i k b) - \exp (2 i k a) \exp (- i k b)) = C (\exp (q b) + \exp (- q b)) \\ i k B (\exp (i k b) + \exp (2 i k a) \exp (- i k b)) = q C (\exp (q b) - \exp (- q b)) \end{cases} \\ \frac{\exp (i k b) - \exp (i k (2 a - b))}{i k (\exp (i k b) + \exp (i k (2 a - b)))} = \frac{\exp (q b) + \exp (- q b)}{q (\exp (q b) - \exp (- q b))} \\ \frac{\exp (2 i k b) - \exp (2 i k a)}{i k (\exp (2 i k b) + \exp (2 i k a))} = \frac{\exp (q b) + \exp (- q b)}{q (\exp (q b) - \exp (- q b))} \\ \frac{q}{i k} \frac{- 2 i \sin (2 k a - 2 k b)}{2 + 2 \cos (2 k a - 2 k b)} = \frac{e^{q b} + e^{- q b}}{e^{q b} - e^{- q b}} \\ - \frac{q}{k} \frac{\sin (k a - k b)}{\cos (k a - k b)} = \frac{e^{q b} + e^{- q b}}{e^{q b} - e^{- q b}} \\ q (e^{q b} - e^{- q b}) \sin (k a - k b) + k (e^{q b} + e^{- q b}) \cos (k a - k b) = 0 \end{array}$

La ecuación transcendente que nos proporciona los niveles de energía correspondiente a las funciones de onda simétricas, es

$q \sinh (q b) \sin (k a - k b) + k \cosh (q b) \cos (k a - k b) = 0$

Antisimétricas

$\begin{array}{l} {\begin{cases} ψ_{I} (- x) = - ψ_{I I I} (x) \\ ψ_{I I} (- x) = ψ_{I I} (x) \end{cases} \\ ψ_{I} (x) = - A \exp (i k x) - B \exp (- i k x) \\ ψ_{I I} (x) = C \exp (q x) - C \exp (- q x) \\ ψ_{I I I} (x) = B \exp (i k x) + A \exp (- i k x) \end{array}$

En x=a, el potencial es infinito,

$ψ_{I I I} (a) = B \exp (i k a) + A \exp (- i k a) = 0$

La función de onda es continua en x=b y también su derivada primera

$\begin{array}{l} {\begin{cases} B \exp (i k b) + A \exp (- i k b) = C \exp (q b) - C \exp (- q b) \\ i k B \exp (i k b) - i k A \exp (- i k b) = C q \exp (q b) + C q \exp (- q b) \end{cases} \\ - \frac{q}{k} \frac{\sin (k a - k b)}{\cos (k a - k b)} = \frac{e^{q b} - e^{- q b}}{e^{q b} + e^{- q b}} \\ q (e^{q b} + e^{- q b}) \sin (k a - k b) + k (e^{q b} - e^{- q b}) \cos (k a - k b) = 0 \end{array}$

La ecuación transcendente que nos proporciona los niveles de energía correspondiente a las funciones de onda simétricas, es

$q \cosh (q b) \sin (k a - k b) + k \sinh (q b) \cos (k a - k b) = 0$

Energía, E>V₀

En la región I

$\begin{array}{l} \frac{d^{2} ψ (x)}{d x^{2}} + \frac{2 m}{ℏ^{2}} E \cdot ψ (x) = 0, k^{2} = \frac{2 m}{ℏ^{2}} E \\ ψ_{I} (x) = A_{1} e^{i k x} + B_{1} e^{- i k x} \end{array}$

En la región II

$\begin{array}{l} - \frac{ℏ^{2}}{2 m} \frac{d^{2} ψ (x)}{d x^{2}} + V_{0} \cdot ψ (x) = E \cdot ψ (x) \\ \frac{d^{2} ψ (x)}{d x^{2}} + \frac{2 m}{ℏ^{2}} (E - V_{0}) ψ (x) = 0, q^{2} = \frac{2 m}{ℏ^{2}} (E - V_{0}), E > V_{0} \\ ψ_{I I} (x) = C e^{i q x} + D e^{- i q x} \end{array}$

En la región III

$\begin{array}{l} \frac{d^{2} ψ (x)}{d x^{2}} + \frac{2 m}{ℏ^{2}} E \cdot ψ (x) = 0, k^{2} = \frac{2 m}{ℏ^{2}} E \\ ψ_{I I I} (x) = A_{2} e^{i k x} + B_{2} e^{- i k x} \end{array}$

Niveles de energía

Las funciones de onda pueden ser

Simétricas

$\begin{array}{l} {\begin{cases} ψ_{I} (- x) = ψ_{I I I} (x) \\ ψ_{I I} (- x) = ψ_{I I} (x) \end{cases} \\ ψ_{I} (x) = A \exp (i k x) + B \exp (- i k x) \\ ψ_{I I} (x) = C \exp (i q x) + C \exp (- i q x) \\ ψ_{I I I} (x) = B \exp (i k x) + A \exp (- i k x) \end{array}$

En x=a, el potencial es infinito,

$ψ_{I I I} (a) = B \exp (i k a) + A \exp (- i k a) = 0$

La función de onda es continua en x=b y también su derivada primera

En vez de volver a realizar el cálculo completo, basta sustituir en la correspondeinte ecuación transcencente

$q \to i q, q^{2} = \frac{2 m}{ℏ^{2}} (E - V_{0})$

La ecuación ecuación transcendente, para los niveles de energía E>V₀, es

$\begin{array}{l} i q (e^{i q b} - e^{- i q b}) \sin (k a - k b) + k (e^{i q b} + e^{- i q b}) \cos (k a - k b) = 0 \\ i q (2 i \sin (q b)) \sin (k a - k b) + k (2 \cos (q b)) \cos (k a - k b) = 0 \\ k \cos (q b) \cos (k a - k b) - q \sin (q b) \sin (k a - k b) = 0 \end{array}$

Antisimétricas

$\begin{array}{l} {\begin{cases} ψ_{I} (- x) = - ψ_{I I I} (x) \\ ψ_{I I} (- x) = - ψ_{I I} (x) \end{cases} \\ ψ_{I} (x) = - A \exp (i k x) - B \exp (- i k x) \\ ψ_{I I} (x) = C \exp (i q x) - C \exp (- i q x) \\ ψ_{I I I} (x) = B \exp (i k x) + A \exp (- i k x) \end{array}$

La ecuación ecuación transcendente, para los niveles de energía E>V₀, es

$\begin{array}{l} i q (e^{i q b} + e^{- i q b}) \sin (k a - k b) + k (e^{i q b} - e^{- i q b}) \cos (k a - k b) = 0 \\ i q (2 \cos (k b)) \sin (k a - k b) + k (2 i \sin (k b)) \cos (k a - k b) = 0 \\ q \cos (k b) \sin (k a - k b) + k \sin (k b) \cos (k a - k b) = 0 \end{array}$

Cálculo de los niveles de energía

Establecemos un sistema de unidades tal que ℏ=m=1.

Representamos los primeros niveles de energía de un pozo infinito de potencial de anchura 2a=π con el fin de apreciar el efecto de la barrera de potencial

$E = n^{2} \frac{π^{2} ℏ^{2}}{8 m a^{2}}, n = 1,2,3...$

a=pi/2; %mitad de la anchura del pozo infinito
Emax=15;
hold on
xx=[-a-0.1, -a, -a,a,a, a+0.1, a+0.1, -a-0.1, -a-0.1];
yy=[Emax, Emax, 0, 0, Emax, Emax, -1, -1, Emax ];
fill(xx,yy, [0.5 0.5 0.5])
for n=1:5
    E=n^2*pi^2/(8*a^2);
    text(a, E,num2str(E),'VerticalAlignment','bottom', 'HorizontalAlignment',
'right')
    line([-a,a],[E,E],'color','b')
end
hold off
ylim([-1,Emax])
xlabel('')
ylabel('E')
title('Niveles de energía')

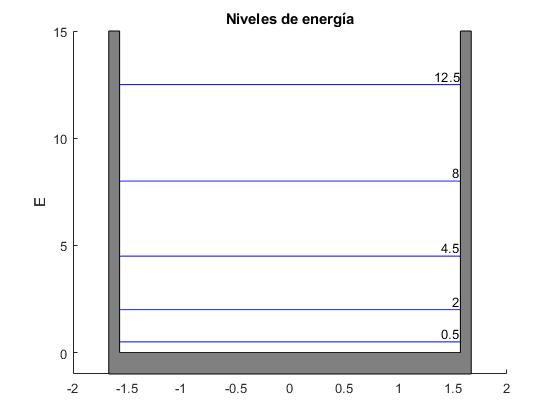
Introducimos en el pozo infinito de potencial de anchura 2a=π una barrera de altura V₀=10 y de anchura 2b=0.75. Utilizamos la función raices para obtener las raíces de la ecuación transcendente. Representamos la función potencial V(x) y los niveles de energía

function semi_3
    V0=10; %altura barrera
    a=pi/2; %mitad anchura del pozo
    b=0.75/2; %mitad de la anchura de la barrera
    Emax=30;
    %niveles de energía
    %E<V0
    fi=@(E) (sqrt(2*V0-2*E).*cosh(sqrt(2*V0-2*E)*b)).*sin(sqrt(2*E)*(a-b))
+(sqrt(2*E).*sinh(sqrt(2*V0-2*E)*b)).*cos(sqrt(2*E)*(a-b));
    fp=@(E) (sqrt(2*V0-2*E).*sinh(sqrt(2*V0-2*E)*b)).*sin(sqrt(2*E)*(a-b))+
(sqrt(2*E).*cosh(sqrt(2*V0-2*E)*b)).*cos(sqrt(2*E)*(a-b));
    x=linspace(0,V0, 40);
    impar_1=raices(fi,x);
    par_1=raices(fp,x);
    % E>V0
    ffi=@(E) sqrt(2*E-2*V0).*cos(sqrt(2*E-2*V0)*b).*sin(sqrt(2*E)*(a-b))+
sqrt(2*E).*sin(sqrt(2*E-2*V0)*b).*cos(sqrt(2*E)*(a-b));
    ffp=@(E) sqrt(2*E-2*V0).*sin(sqrt(2*E-2*V0)*b).*sin(sqrt(2*E)*(a-b))-
sqrt(2*E).*cos(sqrt(2*E-2*V0)*b).*cos(sqrt(2*E)*(a-b));
    x=linspace(V0, Emax, 40);
    par_2=raices(ffp,x);
    impar_2=raices(ffi,x);
    niveles=sort([par_1, impar_1, par_2, impar_2]);
    hold on
    xx=[-a-0.1, -a, -a,-b,-b, b, b,a,a,a+0.1, a+0.1,-a-0.1, -a-0.1];
    yy=[Emax, Emax, 0, 0, V0, V0,0,0,Emax, Emax,-1, -1, Emax];
    fill(xx,yy, [0.5 0.5 0.5])
    i=1;
    for E=niveles
        line([-a,a],[E,E],'color','b')
        if rem(i,2)==0
            text(a, E,num2str(E),'VerticalAlignment','bottom', 
'HorizontalAlignment','right')
        else
            text(-a, E,num2str(E),'VerticalAlignment','bottom', 
'HorizontalAlignment','left')
        end
        i=i+1;
    end
    hold off
    ylim([-1,Emax])
    xlabel('')
    ylabel('E')
    title('Niveles de energía')

    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

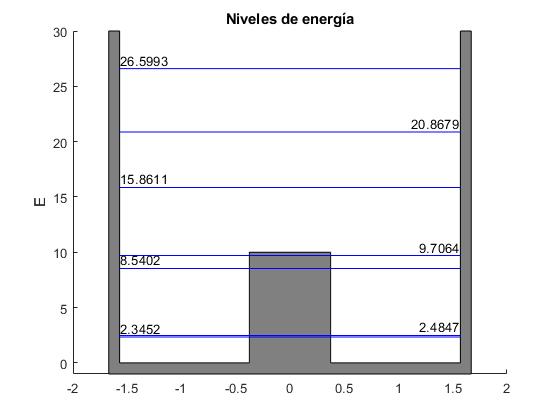
A la izquierda, la energía de los niveles correspondientes a funciones de onda simétricas y a la derecha, antisimétricas

Funciones de onda

Vamos a representar las funciones de onda correspondientes a los niveles de energía en cada uno de los cuatro casos. Para ello, tenemos que relacionar los coeficientes B y C con el coeficiente A. El coeficiente A se calcula de modo que

$\int_{0}^{b} ψ_{I I} (x) ψ_{I I}^{*} (x) \cdot d x + \int_{b}^{a} ψ_{I I I} (x) ψ_{I I I}^{*} (x) \cdot d x = \frac{1}{2}$

El resultado 1/2 se debe a razones de simetría de la función de onda. El segundo término no cambia

$\begin{array}{l} \int_{b}^{a} ψ_{I I I} (x) ψ_{I I I}^{*} (x) \cdot d x = \int_{b}^{a} (B e^{i k x} + A e^{- i k x}) (B^{*} e^{- i k x} + A^{*} e^{i k x}) \cdot d x = \\ (A A^{*} + B B^{*}) (a - b) + \frac{B A^{*}}{2 i k} (e^{2 i k a} - e^{2 i k b}) - \frac{A B^{*}}{2 i k} (e^{- 2 i k a} - e^{- 2 i k b}) \end{array}$

En el extremo x=a, la relación entre los coeficientes A y B es

$\begin{array}{l} B \exp (i k a) + A \exp (- i k a) = 0 \\ B A^{*} = - A^{2} e^{- 2 i k a} \\ A B^{*} = - A^{2} e^{2 i k a} \\ A A^{*} + B B^{*} = 2 A^{2} \end{array}$

El resultado de la integral es

$\int_{b}^{a} ψ_{I I I} (x) ψ_{I I I}^{*} (x) \cdot d x = A^{2} (2 (a - b) - \frac{\sin (2 k (a - b))}{k})$

Las funciones de onda para E<V₀ y E>V₀ son

E<V₀

Simétricas

${\begin{cases} ψ_{I} (x) = A \exp (i k x) + B \exp (- i k x), - a < x < - b \\ ψ_{I I} (x) = C \exp (q x) + C \exp (- q x), - b \leq x < b \\ ψ_{I I I} (x) = B \exp (i k x) + A \exp (- i k x), b \leq x < a \end{cases}$

El primer término vale

$\begin{array}{l} \int_{0}^{b} ψ_{I I} (x) ψ_{I I}^{*} (x) \cdot d x = C C^{*} \int_{0}^{b} {(e^{q x} + e^{- q x})}^{2} \cdot d x = \\ C C^{*} (\frac{e^{2 q b}}{2 q} - \frac{e^{- 2 q b}}{2 q} + 2 b) = C C^{*} (\frac{\sinh (2 q b)}{q} + 2 b) \end{array}$

Las relaciones entre los coeficientes C y B con A son

$\begin{array}{l} {\begin{cases} B \exp (i k a) + A \exp (- i k a) = 0 \\ B \exp (i k b) + A \exp (- i k b) = C \exp (q b) + C \exp (- q b) \end{cases} \\ C = \frac{B e^{i k b} + A e^{- i k b}}{e^{q b} + e^{- q b}} \\ C C^{*} = \frac{\sin^{2} (k (a - b))}{\cosh^{2} (q b)} A^{2} \end{array}$

El resultado es

$\int_{0}^{b} ψ_{I I} (x) ψ_{I I}^{*} (x) \cdot d x = A^{2} \frac{\sin^{2} (k (a - b))}{\cosh^{2} (q b)} (\frac{\sinh (2 q b)}{q} + 2 b)$

Antisimétricas

${\begin{cases} ψ_{I} (x) = - A \exp (i k x) - B \exp (- i k x), - a < x < - b \\ ψ_{I I} (x) = C \exp (q x) - C \exp (- q x), - b \leq x < b \\ ψ_{I I I} (x) = B \exp (i k x) + A \exp (- i k x), b \leq x < a \end{cases}$

El primer término vale

$\begin{array}{l} \int_{0}^{b} ψ_{I I} (x) ψ_{I I}^{*} (x) \cdot d x = C C^{*} \int_{0}^{b} {(e^{q x} - e^{- q x})}^{2} \cdot d x = \\ C C^{*} (\frac{e^{2 q b}}{2 q} - \frac{e^{- 2 q b}}{2 q} - 2 b) = C C^{*} (\frac{\sinh (2 q b)}{q} - 2 b) \end{array}$

Las relaciones entre los coeficientes C y B con A son

$\begin{array}{l} {\begin{cases} B \exp (i k a) + A \exp (- i k a) = 0 \\ B \exp (i k b) + A \exp (- i k b) = C \exp (q b) - C \exp (- q b) \end{cases} \\ C = \frac{e^{- i k b} - e^{- 2 i k a} e^{i k b}}{e^{q b} - e^{- q b}} A \\ C C^{*} = \frac{\sin^{2} (k (a - b))}{\sinh^{2} (q b)} A^{2} \end{array}$

El resultado es

$\int_{0}^{b} ψ_{I I} (x) ψ_{I I}^{*} (x) \cdot d x = A^{2} \frac{\sin^{2} (k (a - b))}{\sinh^{2} (q b)} (\frac{\sinh (2 q b)}{q} - 2 b)$

E>V₀

Simétricas

${\begin{cases} ψ_{I} (x) = A \exp (i k x) + B \exp (- i k x), - a < x < - b \\ ψ_{I I} (x) = C \exp (i q x) + C \exp (- i q x), - b \leq x < b \\ ψ_{I I I} (x) = B \exp (i k x) + A \exp (- i k x), b \leq x < a \end{cases}$

El primer término vale

$\int_{0}^{b} ψ_{I I} (x) ψ_{I I}^{*} (x) \cdot d x = C C^{*} \int_{0}^{b} (2 + e^{- 2 i q x} + e^{2 i q x}) \cdot d x = C C^{*} (2 b + \frac{\sin (2 q b)}{q})$

Las relaciones entre los coeficientes C y B con A son

$\begin{array}{l} {\begin{cases} B \exp (i k a) + A \exp (- i k a) = 0 \\ B \exp (i k b) + A \exp (- i k b) = C \exp (i q b) + C \exp (- i q b) \end{cases} \\ C = \frac{e^{- i k b} - e^{i k b} e^{- 2 i k a}}{e^{i q b} + e^{- i q b}} \\ C C^{*} = A^{2} \frac{\sin^{2} (k (a - b))}{\cos^{2} (q b)} \end{array}$

El resultado es

$\int_{0}^{b} ψ_{I I} (x) ψ_{I I}^{*} (x) \cdot d x = A^{2} \frac{\sin^{2} (k (a - b))}{\cos^{2} (q b)} (\frac{\sin (2 q b)}{q} + 2 b)$

Antisimétricas

${\begin{cases} ψ_{I} (x) = - A \exp (i k x) - B \exp (- i k x), - a < x < - b \\ ψ_{I I} (x) = C \exp (i q x) - C \exp (- i q x), - b \leq x < b \\ ψ_{I I I} (x) = B \exp (i k x) + A \exp (- i k x), b \leq x < a \end{cases}$

El primer término vale

$\int_{0}^{b} ψ_{I I} (x) ψ_{I I}^{*} (x) \cdot d x = C C^{*} \int_{0}^{b} (2 - e^{- 2 i q x} - e^{2 i q x}) \cdot d x = C C^{*} (2 b - \frac{\sin (2 q b)}{q})$

Las relaciones entre los coeficientes C y B con A son

$\begin{array}{l} {\begin{cases} B \exp (i k a) + A \exp (- i k a) = 0 \\ B \exp (i k b) + A \exp (- i k b) = C \exp (i q b) - C \exp (- i q b) \end{cases} \\ C = \frac{e^{- i k b} - e^{i k b} e^{- 2 i k a}}{e^{i q b} - e^{- i q b}} \\ C C^{*} = A^{2} \frac{\sin^{2} (k (a - b))}{\sin^{2} (q b)} \end{array}$

El resultado es

$\int_{0}^{b} ψ_{I I} (x) ψ_{I I}^{*} (x) \cdot d x = A^{2} \frac{\sin^{2} (k (a - b))}{\sin^{2} (q b)} (- \frac{\sin (2 q b)}{q} + 2 b)$

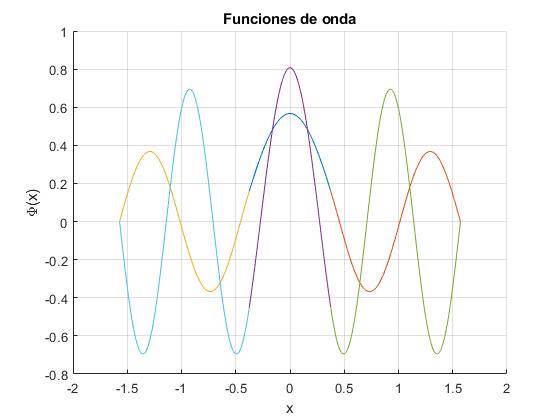
Representamos las funciones de onda de de un pozo infinito de potencial de anchura 2a=π con una barrera de altura V₀=10 y de anchura 2b=0.75.

A continuación, el código que calcula los niveles de energía y los guarda en un vector

E<V₀

Simétricas, par_1
Antisimétricas, impar_1

E>V₀

Simétricas, par_2
Antisimétricas, impar_2

function semi_5
    V0=10;
    a=pi/2;
    b=0.75/2;
    Emax=30;
    %Niveles de energía
    %E<V0
    fi=@(E) (sqrt(2*V0-2*E).*cosh(sqrt(2*V0-2*E)*b)).*sin(sqrt(2*E)*(a-b))
+(sqrt(2*E).*sinh(sqrt(2*V0-2*E)*b)).*cos(sqrt(2*E)*(a-b));
    fp=@(E) (sqrt(2*V0-2*E).*sinh(sqrt(2*V0-2*E)*b)).*sin(sqrt(2*E)*(a-b))
+(sqrt(2*E).*cosh(sqrt(2*V0-2*E)*b)).*cos(sqrt(2*E)*(a-b));
    x=linspace(0,V0, 40);
    impar_1=raices(fi,x);
    par_1=raices(fp,x);

    % E>V0
    ffi=@(E) sqrt(2*E-2*V0).*cos(sqrt(2*E-2*V0)*b).*sin(sqrt(2*E)*(a-b))
+sqrt(2*E).*sin(sqrt(2*E-2*V0)*b).*cos(sqrt(2*E)*(a-b));
    ffp=@(E) sqrt(2*E-2*V0).*sin(sqrt(2*E-2*V0)*b).*sin(sqrt(2*E)*(a-b))
-sqrt(2*E).*cos(sqrt(2*E-2*V0)*b).*cos(sqrt(2*E)*(a-b));
    x=linspace(V0, Emax, 40);
    par_2=raices(ffp,x);
    impar_2=raices(ffi,x);
    hold on
    %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 
    %Situar aquí el código que representa las funciones de onda
    %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    hold off
    grid on
    xlabel('x')
    ylabel('\Phi(x)')
    title('Funciones de onda')

    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end

end

El código para representar las funciones de onda se introduce en el lugar señalado

E<V₀

Simétricas

...
 for E=par_1 
      k=sqrt(2*E);
      q=sqrt(2*V0-2*E);
      suma=2*(a-b)-sin(2*k*(a-b))/k+sin(k*(a-b))^2*(sinh(2*q*b)/q+2*b)
/cosh(q*b)^2;
      A=1/sqrt(2*suma);
      B=-A*exp(-1i*2*k*a);
      C=(B*exp(1i*k*b)+A*exp(-1i*k*b))/(2*cosh(q*b));
      fplot(@(x) real(C*(exp(q*x)+exp(-q*x))),[-b,b])
      fplot(@(x) real(B*exp(1i*k*x)+A*exp(-1i*k*x)),[b,a])
      fplot(@(x) real(A*exp(1i*k*x)+B*exp(-1i*k*x)),[-a,-b])
  end
  disp(par_1)
...

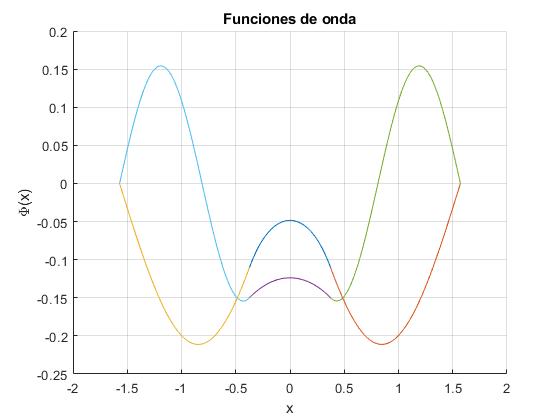
2.3452    8.5402

Antisimétricas

...
    for E=impar_1 
      k=sqrt(2*E);
      q=sqrt(2*V0-2*E);
      suma=2*(a-b)-sin(2*k*(a-b))/k+sin(k*(a-b))^2*(sinh(2*q*b)/q-2*b)
/sinh(q*b)^2;
      A=1/sqrt(2*suma);
      B=-A*exp(-1i*2*k*a);
      C=(B*exp(1i*k*b)+A*exp(-1i*k*b))/(2*sinh(q*b));
      fplot(@(x) real(C*(exp(q*x)-exp(-q*x))),[-b,b])
      fplot(@(x) real(B*exp(1i*k*x)+A*exp(-1i*k*x)),[b,a])
      fplot(@(x) real(-A*exp(1i*k*x)-B*exp(-1i*k*x)),[-a,-b])
    end
    disp(impar_1)
...

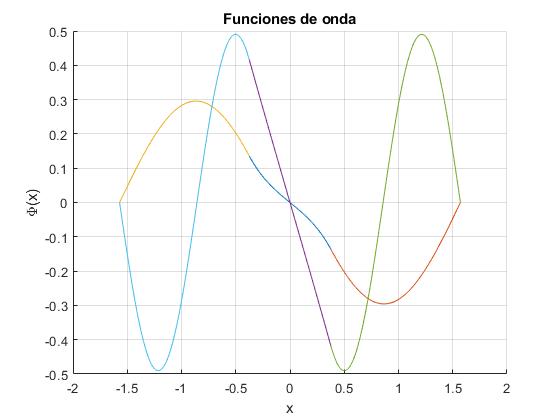
 2.4847    9.7064

E>V₀

Simétricas

...
    for E=par_2 %E>V0
      k=sqrt(2*E);
      q=sqrt(2*E-2*V0);
      suma=2*(a-b)-sin(2*k*(a-b))/k+sin(k*(a-b))^2*(sin(2*q*b)/q+2*b)
/cos(q*b)^2;
      A=1/sqrt(2*suma);
      B=-A*exp(-1i*2*k*a);
      C=(B*exp(1i*k*b)+A*exp(-1i*k*b))/(exp(1i*q*b)+exp(-1i*q*b));
      fplot(@(x) real(C*(exp(1i*q*x)+exp(-1i*q*x))),[-b,b])
      fplot(@(x) real(B*exp(1i*k*x)+A*exp(-1i*k*x)),[b,a])
      fplot(@(x) real(A*exp(1i*k*x)+B*exp(-1i*k*x)),[-a,-b])
    end
    disp(par_2)
    ...

 15.8611   26.5993

Antisimétricas

...
    for E=impar_2 %E>V0
      k=sqrt(2*E);
      q=sqrt(2*E-2*V0);
      suma=2*(a-b)-sin(2*k*(a-b))/k+sin(k*(a-b))^2*(-sin(2*q*b)/q+2*b)
/sin(q*b)^2;
      A=1/sqrt(2*suma);
      B=-A*exp(-1i*2*k*a);
      C=(B*exp(1i*k*b)+A*exp(-1i*k*b))/(exp(1i*q*b)-exp(-1i*q*b));
      fplot(@(x) real(C*(exp(1i*q*x)-exp(-1i*q*x))),[-b,b])
      fplot(@(x) real(B*exp(1i*k*x)+A*exp(-1i*k*x)),[b,a])
      fplot(@(x) real(-A*exp(1i*k*x)-B*exp(-1i*k*x)),[-a,-b])
    end
    disp(impar_2)
            ...

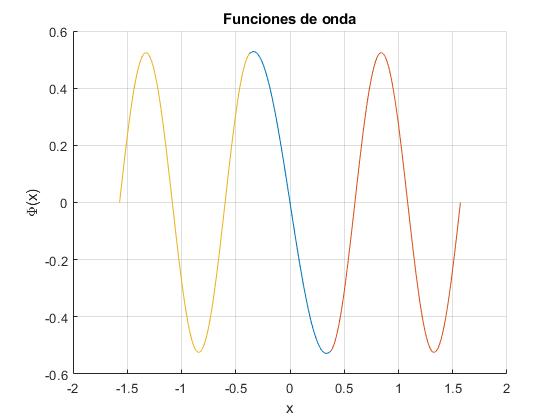
 20.8679

Una variante del pozo de potencial de profundidad infinita

En esta sección, vamos a calcular los niveles de energía y las correspondientes funciones de onda del siguiente pozo de potencial de profundidad infinita.

Para crear parte de la figura se ha utilizado el código

x=[0,0,2,2,5,5,7,7,10,10,12,12,14,14];
y=[25,0,0,-20,-20,5,5,16,16,-8,-8,2,2,25];
plot(x,y,'k','lineWidth',1.5)
xlim([-1,15])
ylim([-21,25])
xlabel('x')
ylabel('E_p(x)')
title('Potencial')

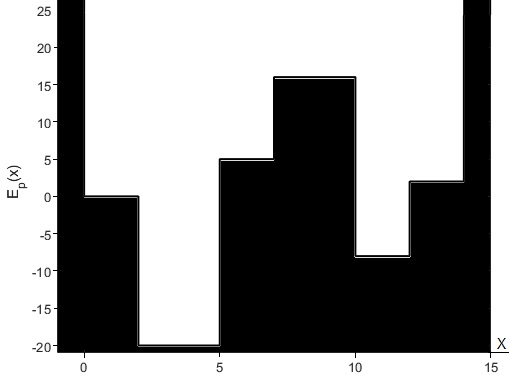
Donde la energía potencial se mide en eV (1.6021·10^-19 J) y la posición x en ángstrom Å (10^-10 m). El potencial V(x) es infinito en x=0 y x=14 Å y consta de N=6 intervalos de potencial constante

$V (x) = {\begin{cases} 0 < x \leq 2, 0 \\ 2 < x \leq 5, - 20 \\ 5 < x \leq 7, 5 \\ 7 < x \leq 10, 16 \\ 10 < x \leq 12, - 8 \\ 12 < x < 14, 2 \end{cases}$

La ecuación de Schrödinger es

$- \frac{ℏ^{2}}{2 m} \frac{d^{2} Ψ}{d x^{2}} + V (x) Ψ = E Ψ$

Dividimos ambos miembros por V_m, el máximo potencial no infinito y distinto de cero, en este ejemplo, V_m=16 eV. Definimos

la energía adimensional e=E/V_m
el potencial adimensional en cada intervalo v_i=V(x)/V_m, con i=1, 2, 3, ...N.
la distancia adimensional ξ

$ξ = \frac{\sqrt{2 m V_{m}}}{ℏ} x$

La ecuación de Schrödinger se transforma en otra más simple y apropiada para el cálculo numérico

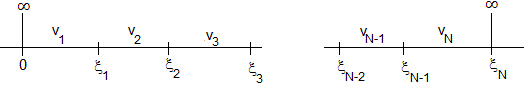
$\begin{array}{l} - \frac{ℏ^{2}}{2 m V_{m}} \frac{d^{2} Ψ}{d x^{2}} + \frac{V (x)}{V_{m}} Ψ = \frac{E}{V_{m}} Ψ \\ \frac{d^{2} Ψ}{d ξ^{2}} + (e - v_{i}) Ψ = 0 \end{array}$

La solución de esta ecuación diferencial en un intervalo i de potencial constante v_i comprendido entre ξ_i-1 y ξ_i es

$Ψ_{i} = A_{i} f_{i} (ξ) + B_{i} g_{i} (ξ)$

		f_i	g_i	f'_i	g'_i
e<v_i	$k_{i} = \sqrt{v_{i} - e}$	$\exp (k_{i} ξ)$	$\exp (- k_{i} ξ)$	$k_{i} \exp (k_{i} ξ)$	$- k_{i} \exp (- k_{i} ξ)$
e>v_i	$k_{i} = \sqrt{e - v_{i}}$	$- k_{i} \exp (- k_{i} ξ)$	$\cos (k_{i} ξ)$	$k_{i} \cos (k_{i} ξ)$	$- k_{i} \sin (k_{i} ξ)$
e=v_i		ξ	1	1	0

Las dos últimas columnas, corresponden a las derivadas de f_i(ξ) y g_i(ξ) respecto de ξ

La solución exponencial, corresponde a una partícula que penetra a través de una barrera e<v_i
la solución trigonométrica, a una barrera cuya altura es menor que la energía de la partícula e>v_i.
El tercer caso e=v_i es posible, pero muy improbable

Niveles de energía

Con N intervalos, hay 2N coeficientes A_i y B_i que tenemos que determinar

En los extremos el potencial es infinito, la función de onda es nula, Ψ(0)=0, Ψ(ξ_N)=0
En las posiciones ξ₁, ξ₂, ...ξ_N-1, la función de onda deberá ser continua y también su derivada primera

$\begin{array}{l} ψ_{i} (ξ_{i}) = ψ_{i + 1} (ξ_{i}) \\ {\frac{d ψ_{i}}{d ξ} |}_{ξ_{i}} = {\frac{d ψ_{i + 1}}{d ξ} |}_{ξ_{i}} \end{array}} i = 1,... N - 1$

Estas dos condiciones generan el sistema de ecuaciones

$\begin{array}{l} A_{1} f_{1} (0) + B_{1} g_{1} (0) = 0 \\ {\begin{cases} A_{1} f_{1} (ξ_{1}) + B_{1} g_{1} (ξ_{1}) = A_{2} f_{2} (ξ_{1}) + B_{2} g_{2} (ξ_{1}) \\ A_{1} f_{1}^{'} (ξ_{1}) + B_{1} g_{1}^{'} (ξ_{1}) = A_{2} f_{2}^{'} (ξ_{1}) + B_{2} g_{2}^{'} (ξ_{1}) \end{cases} \\ {\begin{cases} A_{2} f_{2} (ξ_{2}) + B_{2} g_{2} (ξ_{2}) = A_{3} f_{3} (ξ_{2}) + B_{3} g_{3} (ξ_{2}) \\ A_{2} f_{2}^{'} (ξ_{2}) + B_{2} g_{2}^{'} (ξ_{2}) = A_{3} f_{3}^{'} (ξ_{2}) + B_{3} g_{3}^{'} (ξ_{2}) \end{cases} \\ ....... \\ {\begin{cases} A_{N - 1} f_{N - 1} (ξ_{N - 1}) + B_{N - 1} g_{N - 1} (ξ_{N - 1}) = A_{N} f_{N} (ξ_{N - 1}) + B_{N} g_{N} (ξ_{N - 1}) \\ A_{N - 1} f_{N - 1}^{'} (ξ_{N - 1}) + B_{N - 1} g_{N - 1}^{'} (ξ_{N - 1}) = A_{N} f_{N}^{'} (ξ_{N - 1}) + B_{N} g_{N}^{'} (ξ_{N - 1}) \end{cases} \\ A_{N} f_{N} (ξ_{N}) + B_{N} g_{N} (ξ_{N}) = 0 \end{array}$

Tenemos un sistema homogéneo de 2N ecuaciones con 2N incógnitas, en forma matricial se escribe

$(\begin{matrix} f_{1} (0) & g_{1} (0) & 0 & 0 & 0 & 0 & ... & 0 & 0 & 0 & 0 \\ f_{1} (ξ_{1}) & g_{1} (ξ_{1}) & - f_{2} (ξ_{1}) & - g_{2} (ξ_{1}) & 0 & 0 & ... & 0 & 0 & 0 & 0 \\ f_{1}^{'} (ξ_{1}) & g_{1}^{'} (ξ_{1}) & - f_{2}^{'} (ξ_{1}) & - g_{2}^{'} (ξ_{1}) & 0 & 0 & ... & 0 & 0 & 0 & 0 \\ 0 & 0 & f_{2} (ξ_{2}) & g_{2} (ξ_{2}) & - f_{3} (ξ_{2}) & - g_{3} (ξ_{2}) & ... & 0 & 0 & 0 & 0 \\ 0 & 0 & f_{2}^{'} (ξ_{2}) & g_{2}^{'} (ξ_{2}) & - f_{3}^{'} (ξ_{2}) & - g_{3}^{'} (ξ_{2}) & ... & 0 & 0 & 0 & 0 \\ ... & ... & ... & ... & ... & ... & ... & ... & ... & ... & ... \\ 0 & 0 & 0 & 0 & 0 & ... & f_{N - 1} (ξ_{N - 1}) & g_{N - 1} (ξ_{N - 1}) & - f_{N} (ξ_{N - 1}) & - g_{N} (ξ_{N - 1}) \\ 0 & 0 & 0 & 0 & 0 & ... & f_{N - 1}^{'} (ξ_{N - 1}) & g_{N - 1}^{'} (ξ_{N - 1}) & - f_{N}^{'} (ξ_{N - 1}) & - g_{N}^{'} (ξ_{N - 1}) \\ 0 & 0 & 0 & 0 & 0 & ... & 0 & 0 & f_{N} (ξ_{N}) & g_{N} (ξ_{N}) \end{matrix}) (\begin{matrix} A_{1} \\ B_{1} \\ A_{2} \\ B_{2} \\ A_{3} \\ B_{3} \\ ... \\ A_{N - 1} \\ B_{N - 1} \\ A_{N} \\ B_{N} \end{matrix}) = 0$

El determinante de los coeficientes deberá ser cero, lo que determina los niveles de energía

function pozo_potencial
    Vm=16;  %máximo
    K=sqrt(2*9.1091e-31*Vm*1.6021e-19)*1e-10/1.0545e-34;
    x=[2,5,7,10,12,14]*K;
    v=[0,-20,5,16,-8,2]/Vm;
    N=length(v);
    C=zeros(2*N);
    
%niveles de energía
    xb=buscar_intervalos(@energia,-20/Vm, 25/Vm,50);
    nb=size(xb);
    nivel=zeros(1,nb(1));
    disp('niveles de energia')
    for m=1:nb(1)
        nivel(m)=fzero(@energia,[xb(m,1),xb(m,2)]);
    end
    disp(nivel')
    
    xx=[0,0,x(1),x(1),x(2),x(2),x(3),x(3),x(4),x(4),x(5),x(5),x(6),x(6)];
    yy=[2,v(1),v(1),v(2),v(2),v(3),v(3),v(4),v(4),v(5),v(5),v(6),v(6),2];
    plot(xx,yy,'k','lineWidth',1.5)
    for m=1:nb(1)
        line([0,x(6)],[nivel(m), nivel(m)],'color','r')
    end
    grid on
    xlabel('\xi')
    ylabel('E_p(\xi)')
    title('Niveles de energía')  
    
    
    function res = energia(e)
        if v(1)>e
            C(1,1)=1; C(1,2)=1;
        else
            C(1,1)=0; C(1,2)=1;
        end
        for i=1:N-1
            if v(i)>e
                k=sqrt(v(i)-e);
                C(2*i,2*i-1)=exp(k*x(i)); C(2*i,2*i)=exp(-k*x(i));
                C(2*i+1,2*i-1)=k*exp(k*x(i)); C(2*i+1,2*i)=-k*exp(-k*x(i));
            elseif v(i)<e
                k=sqrt(e-v(i));
                C(2*i,2*i-1)=sin(k*x(i)); C(2*i,2*i)=cos(k*x(i));
                C(2*i+1,2*i-1)=k*cos(k*x(i)); C(2*i+1,2*i)=-k*sin(k*x(i));
            else
                C(2*i,2*i-1)=x(i); C(2*i,2*i)=1;
                C(2*i+1,2*i-1)=1; C(2*i+1,2*i)=0;
            end
            if v(i+1)>e
                k=sqrt(v(i+1)-e);
                C(2*i,2*i+1)=-exp(k*x(i)); C(2*i,2*i+2)=-exp(-k*x(i));
                C(2*i+1,2*i+1)=-k*exp(k*x(i)); C(2*i+1,2*i+2)=k*exp(-k*x(i));
            elseif v(i+1)<e
                k=sqrt(e-v(i+1));
                C(2*i,2*i+1)=-sin(k*x(i)); C(2*i,2*i+2)=-cos(k*x(i));
                C(2*i+1,2*i+1)=-k*cos(k*x(i)); C(2*i+1,2*i+2)=k*sin(k*x(i));
            else
                C(2*i,2*i+1)=-x(i); C(2*i,2*i+2)=-1;
                C(2*i+1,2*i+1)=-1; C(2*i+1,2*i+2)=0;
            end
        end
        if v(N)>e
            k=sqrt(v(N)-e);
            C(2*N,2*N-1)=exp(k*x(N)); C(2*N,2*N)=exp(-k*x(N));
        elseif v(N)<e
            k=sqrt(e-v(N));
            C(2*N,2*N-1)=sin(k*x(N)); C(2*N,2*N)=cos(k*x(N));
        else
            C(2*N,2*N-1)=x(N); C(2*N,2*N)=1;
        end
        res=det(C);
        C=zeros(2*N);
    end
        
    function xb = buscar_intervalos(f,a,b,n)
        z = linspace(a,b,n);
        j = 0; 
        y1=f(z(1));
        for m = 1:length(z)-1
            y2=f(z(m+1));
            if sign(y1) ~= sign(y2) 
                j = j + 1;
                xb(j,1) = z(m);
                xb(j,2) = z(m+1);
            end
            y1=y2;
        end
        if isempty(xb) 
            disp('no se han encontrado cambios de signo')
        else
        disp(['número de intervalos:' int2str(j)]) 
        end
    end 

end

Representamos la energía potencial E_p(ξ) en función de la variable adimensional ξ, las líneas rojas horizontales corresponden a los niveles de energía adimensionales e=E/V_m

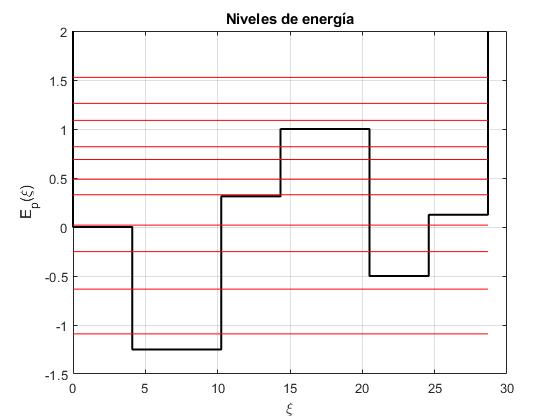
Los niveles de energía en eV son

Funciones de onda

Dado un nivel de energía e, calculamos los coeficientes B₁, A₂, B₂, A₃, B₃....A_N-1, B_N-1, A_N, B_N en función de A₁ que sirve de factor de escala

La primera ecuación nos da B₁

$B_{1} = - \frac{f_{1} (0)}{g_{1} (0)} A_{1}$

Las dos ecuaciones siguientes, A₂ y B₂

$\begin{array}{l} {\begin{cases} A_{2} f_{2} (ξ_{1}) + B_{2} g_{2} (ξ_{1}) = c_{1}, c_{1} = A_{1} f_{1} (ξ_{1}) + B_{1} g_{1} (ξ_{1}) \\ A_{2} f_{2}^{'} (ξ_{1}) + B_{2} g_{2}^{'} (ξ_{1}) = c_{2}, c_{2} = A_{1} f_{1}^{'} (ξ_{1}) + B_{1} g_{1}^{'} (ξ_{1}) \end{cases} \\ A_{2} = \frac{c_{1} g_{2}^{'} (ξ_{1}) - c_{2} g_{2} (ξ_{1})}{f_{2} (ξ_{1}) g_{2}^{'} (ξ_{1}) - f_{2}^{'} (ξ_{1}) g_{2} (ξ_{1})}, B_{2} = \frac{c_{2} f_{2} (ξ_{1}) - c_{1} f_{2}^{'} (ξ_{1})}{f_{2} (ξ_{1}) g_{2}^{'} (ξ_{1}) - f_{2}^{'} (ξ_{1}) g_{2} (ξ_{1})} \end{array}$

y así, con el resto de los coeficientes. Los dos últimas proporcionan A_N y B_N

$\begin{array}{l} {\begin{cases} A_{N} f_{N} (ξ_{N - 1}) + B_{N} g_{N} (ξ_{N - 1}) = c_{1}, c_{1} = A_{N - 1} f_{N - 1} (ξ_{N - 1}) + B_{N - 1} g_{N - 1} (ξ_{N - 1}) \\ A_{N} f_{N}^{'} (ξ_{N - 1}) + B_{N} g_{N}^{'} (ξ_{N - 1}) = c_{2}, c_{2} = A_{N - 1} f_{N - 1}^{'} (ξ_{1}) + B_{N - 1} g_{N - 1}^{'} (ξ_{N - 1}) \end{cases} \\ A_{N} = \frac{c_{1} g_{N}^{'} (ξ_{N - 1}) - c_{2} g_{N} (ξ_{N - 1})}{f_{N} (ξ_{N - 1}) g_{N}^{'} (ξ_{N - 1}) - f_{N}^{'} (ξ_{N - 1}) g_{N} (ξ_{N - 1})}, B_{N} = \frac{c_{2} f_{N} (ξ_{N - 1}) - c_{1} f_{N}^{'} (ξ_{N - 1})}{f_{N} (ξ_{N - 1}) g_{N}^{'} (ξ_{N - 1}) - f_{N}^{'} (ξ_{N - 1}) g_{N} (ξ_{N - 1})} \end{array}$

Primero, calculamos el coeficiente B₁ para cada uno de los posibles casos

${\begin{cases} e < v_{1}, f_{1} (0) = 1, g_{1} (0) = 1, B_{1} = - A_{1} \\ e > v_{1}, f_{1} (0) = 0, g_{1} (0) = 1, B_{1} = 0 \\ e = v_{1}, f_{1} (0) = 0, g_{1} (0) = 1, B_{1} = 0 \end{cases}$

Calculamos c₁ y c₂ para cada uno de los tres posibles casos

${\begin{cases} e < v_{1}, k_{1} = \sqrt{v_{1} - e} {\begin{cases} c_{1} = A_{1} e^{k_{1} ξ_{1}} + B_{1} e^{- k_{1} ξ_{1}} \\ c_{2} = A_{1} k_{1} e^{k_{1} ξ_{1}} - B_{1} k_{1} e^{- k_{1} ξ_{1}} \end{cases} \\ e > v_{1}, k_{1} = \sqrt{e - v_{1}} {\begin{cases} c_{1} = A_{1} \sin (k_{1} ξ_{1}) + B_{1} \cos (k_{1} ξ_{1}) \\ c_{2} = A_{1} k_{1} \cos (k_{1} ξ_{1}) - B_{1} k_{1} \sin (k_{1} ξ_{1}) \end{cases} \\ e = v_{1}, {\begin{cases} c_{1} = A_{1} ξ_{1} + B_{1} \\ c_{2} = A_{1} \end{cases} \end{cases}$

Las expresiones de los coeficientes A₂ y B₂ son

${\begin{cases} e < v_{2}, k_{2} = \sqrt{v_{2} - e}, A_{2} = \frac{c_{1} k_{2} + c_{2}}{2 k_{2}} e^{- k_{2} ξ_{1}}, B_{2} = \frac{c_{1} k_{2} - c_{2}}{2 k_{2}} e^{k_{2} ξ_{1}} \\ e > v_{1}, k_{2} = \sqrt{e - v_{2}}, A_{2} = \frac{c_{1} k_{2} \sin (k_{2} ξ_{1}) + c_{2} \cos (k_{2} ξ_{1})}{2 k_{2}}, B_{2} = \frac{c_{1} k_{2} \cos (k_{2} ξ_{1}) - c_{2} \sin (k_{2} ξ_{1})}{2 k_{2}} \\ e = v_{1}, A_{2} = c_{2}, B_{2} = c_{1} - c_{2} ξ_{1} \end{cases}$

y así, el resto de los coeficientes

Normalización

El coeficiente A₁ se calcula teniendo en cuenta que

$\begin{array}{l} \sum_{i = 1}^{N} \int_{ξ_{i - 1}}^{ξ_{i}} Ψ_{i}^{2} (ξ) d ξ = 1 \\ \sum_{i = 1}^{N} \int_{ξ_{i - 1}}^{ξ_{i}} {(A_{i} f_{i} (ξ) + B_{i} g_{i} (ξ))}^{2} d ξ = 1 \end{array}$

donde ξ_i-1=0. Para cada uno de los tres posibles casos, la expresión de la integral es

${\begin{cases} e < v_{i}, k_{i} = \sqrt{v_{i} - e} \int_{ξ_{i - 1}}^{ξ_{i}} (A_{i}^{2} e^{2 k_{i} ξ} + B_{i}^{2} e^{- 2 k_{i} ξ} + 2 A_{i} B_{i}) d ξ \\ e > v_{i}, k_{i} = \sqrt{e - v_{i}} \int_{ξ_{i - 1}}^{ξ_{i}} (A_{i}^{2} \sin^{2} (k_{i} ξ) + B_{i}^{2} \cos^{2} (k_{i} ξ) + A_{i} B_{i} \sin (2 k_{i} ξ)) d ξ \\ e = v_{i}, \int_{ξ_{i - 1}}^{ξ_{i}} (A_{i}^{2} ξ^{2} + B_{i}^{2} + 2 A_{i} B_{i} ξ) d ξ \end{cases}$

Utilizamos estas dos relaciones trigonométricas para efectuar las integrales de la segunda fila, e>v_i. Las otras son inmediatas

$\cos^{2} x = \frac{1 + \cos (2 x)}{2}, \sin^{2} x = \frac{1 - \cos (2 x)}{2}$

El resultado es

${\begin{cases} e < v_{i}, \frac{A_{i}^{2}}{2 k_{i}} (e^{2 k_{i} ξ_{i}} - e^{2 k_{i} ξ_{i - 1}}) - \frac{B_{i}^{2}}{2 k_{i}} (e^{- 2 k_{i} ξ_{i}} - e^{- 2 k_{i} ξ_{i - 1}}) + 2 A_{i} B_{i} (ξ_{i} - ξ_{i - 1}) \\ e > v_{i}, \frac{A_{i}^{2} + B_{i}^{2}}{2} (ξ_{i} - ξ_{i - 1}) + \frac{A_{i}^{2} - B_{i}^{2}}{2 k_{i}} (\sin (2 k_{i} ξ_{i}) - \sin (2 k_{i} ξ_{i - 1})) - \frac{A_{i} B_{i}}{2 k_{i}} (\cos (2 k_{i} ξ_{i}) - \cos (2 k_{i} ξ_{i - 1})) \\ e = v_{i}, \frac{A_{i}^{2}}{3} (ξ_{i}^{3} - ξ_{i - 1}^{3}) + B_{i}^{2} (ξ_{i} - ξ_{i - 1}) + A_{i} B_{i} (ξ_{i}^{2} - ξ_{i - 1}^{2}) \end{cases}$

Representamos la función de onda correspondiente al nivel n=9. Se proporciona también el dato de su energía e. Para convertirla en eV se ha de multiplicar por V_m=16

function pozo_potencial_1
    Vm=16;  %máximo
    K=sqrt(2*9.1091e-31*Vm*1.6021e-19)*1e-10/1.0545e-34;
    x=[2,5,7,10,12,14]*K;
    v=[0,-20,5,16,-8,2]/Vm;
%matriz de los coeficientes
    N=length(v);
    C=zeros(2*N);
    
%niveles de energía
    xb=buscar_intervalos(@energia,-20/Vm, 25/Vm,50);
    nb=size(xb);
    nivel=zeros(1,nb(1));
    disp('niveles de energia')
    for m=1:nb(1)
        nivel(m)=fzero(@energia,[xb(m,1),xb(m,2)]);
    end
 %función de onda  correspondiente a un nivel de energía
    e=nivel(9); %energía del nivel, cambiar el número de nivel
    A=zeros(1,N);
    B=zeros(1,N);
    A(1)=1;
    if(v(1)>e)
        B(1)=-1;
    else
        B(1)=0;
    end
    for i=1:N-1
        if v(i)>e
            k=sqrt(v(i)-e);
            c1=A(i)*exp(k*x(i))+B(i)*exp(-k*x(i));
            c2=A(i)*k*exp(k*x(i))-B(i)*k*exp(-k*x(i));
       elseif v(i)<e
            k=sqrt(e-v(i));
            c1=A(i)*sin(k*x(i))+B(i)*cos(k*x(i));
            c2=A(i)*k*cos(k*x(i))-B(i)*k*sin(k*x(i));
      else
            c1=A(i)*x(i)+B(i);
            c2=A(i);
      end       
     if v(i+1)>e
            k=sqrt(v(i+1)-e);
            A(i+1)=(c1*k+c2)*exp(-k*x(i))/(2*k);
            B(i+1)=(c1*k-c2)*exp(k*x(i))/(2*k);
       elseif v(i+1)<e
            k=sqrt(e-v(i+1));
            A(i+1)=(c1*k*sin(k*x(i))+c2*cos(k*x(i)))/k;
            B(i+1)=(c1*k*cos(k*x(i))-c2*sin(k*x(i)))/k;
       else
            A(i+1)=c2;
            B(i+1)=c1-c2*x(i);
       end
    end 
%comprobación
%     if v(N)>e
%             k=sqrt(v(N)-e);
%             disp(A(N)*exp(k*x(N))+B(N)*exp(-k*x(N)))
%        elseif v(N)<e
%             k=sqrt(e-v(N));
%             disp(A(N)*sin(k*x(N))+B(N)*cos(k*x(N)))
%        else
%             disp(A(N)*x(N)+B(N)) %próximo a cero
%        end


 %normalización
    suma=0;
    if v(1)>e
        k=sqrt(v(1)-e);
        suma=suma+A(1)^2*(exp(2*k*x(1))-1)/(2*k)-B(1)^2*(exp(-2*k*x(1))-1)
/(2*k)+2*A(1)*B(1)*x(1);
    elseif v(1)<e
        k=sqrt(e-v(1));
        suma=suma+x(1)*(A(1)^2+B(1)^2)/2+(A(1)^2-B(1)^2)*sin(2*k*x(1))
/(2*k)-A(1)*B(1)*(cos(2*k*x(1))-1)/(2*k);
    else
        suma=suma+A(1)^2*x(1)^3/3+B(1)^2*x(1)+A(1)*B(1)*x(1)^2;
    end

    for i=2:N
        if v(i)>e
            k=sqrt(v(i)-e);
            suma=suma+A(i)^2*(exp(2*k*x(i))-exp(2*k*x(i-1)))/(2*k)-B(i)^2*
(exp(-2*k*x(i))-exp(-2*k*x(i-1)))/(2*k)+2*A(i)*B(i)*(x(i)-x(i-1));
        elseif v(i)<e
            k=sqrt(e-v(i));
            suma=suma+(x(i)-x(i-1))*(A(i)^2+B(i)^2)/2+(A(i)^2-B(i)^2)*
(sin(2*k*x(i))-sin(2*k*x(i-1)))/(2*k)-A(i)*B(i)*(cos(2*k*x(i))-
cos(2*k*x(i-1)))/(2*k);
        else
            suma=suma+A(i)^2*(x(i)^3-x(i-1)^3)/3+B(i)^2*(x(i)-x(i-1))+
A(i)*B(i)*(x(i)^2-x(i-1)^2);
        end
            
    end 
    for i=1:N
        A(i)=A(i)/sqrt(suma);
        B(i)=B(i)/sqrt(suma);
    end
    hold on
 %representación gráfica
    if v(1)>e
        k=sqrt(v(1)-e);
        f=@(x) A(1)*exp(k*x)+B(1)*exp(-k*x);
        fplot(f,[0, x(1)])
   elseif v(1)<e
        k=sqrt(e-v(1));
        f=@(x) A(1)*sin(k*x)+B(1)*cos(k*x);
        fplot(f,[0, x(1)])
   else
        f=@(x) A(1)*x+B(1);
        fplot(f,[0, x(1)])
   end
   for i=2:N
       if v(i)>e
            k=sqrt(v(i)-e);
            f=@(x) A(i)*exp(k*x)+B(i)*exp(-k*x);
            fplot(f,[x(i-1), x(i)])
       elseif v(i)<e
            k=sqrt(e-v(i));
            f=@(x) A(i)*sin(k*x)+B(i)*cos(k*x);
            fplot(f,[x(i-1), x(i)])
       else
            f=@(x) A(i)*x+B(i);
            fplot(f,[x(i-1), x(i)])
       end    
  end 
  text(0.5, 0, num2str(e),'VerticalAlignment','top')
 hold off
 grid on
 xlabel('\xi')
 ylabel('\Phi(\xi)')
 title('Función de onda')  
    
    function res = energia(e)
        if v(1)>e
            C(1,1)=1; C(1,2)=1;
        else
            C(1,1)=0; C(1,2)=1;
        end
        for i=1:N-1
            if v(i)>e
                k=sqrt(v(i)-e);
                C(2*i,2*i-1)=exp(k*x(i)); C(2*i,2*i)=exp(-k*x(i));
                C(2*i+1,2*i-1)=k*exp(k*x(i)); C(2*i+1,2*i)=-k*exp(-k*x(i));
            elseif v(i)<e
                k=sqrt(e-v(i));
                C(2*i,2*i-1)=sin(k*x(i)); C(2*i,2*i)=cos(k*x(i));
                C(2*i+1,2*i-1)=k*cos(k*x(i)); C(2*i+1,2*i)=-k*sin(k*x(i));
            else
                C(2*i,2*i-1)=x(i); C(2*i,2*i)=1;
                C(2*i+1,2*i-1)=1; C(2*i+1,2*i)=0;
            end
            if v(i+1)>e
                k=sqrt(v(i+1)-e);
                C(2*i,2*i+1)=-exp(k*x(i)); C(2*i,2*i+2)=-exp(-k*x(i));
                C(2*i+1,2*i+1)=-k*exp(k*x(i)); C(2*i+1,2*i+2)=k*exp(-k*x(i));
            elseif v(i+1)<e
                k=sqrt(e-v(i+1));
                C(2*i,2*i+1)=-sin(k*x(i)); C(2*i,2*i+2)=-cos(k*x(i));
                C(2*i+1,2*i+1)=-k*cos(k*x(i)); C(2*i+1,2*i+2)=k*sin(k*x(i));
            else
                C(2*i,2*i+1)=-x(i); C(2*i,2*i+2)=-1;
                C(2*i+1,2*i+1)=-1; C(2*i+1,2*i+2)=0;
            end
        end
        if v(N)>e
            k=sqrt(v(N)-e);
            C(2*N,2*N-1)=exp(k*x(N)); C(2*N,2*N)=exp(-k*x(N));
        elseif v(N)<e
            k=sqrt(e-v(N));
            C(2*N,2*N-1)=sin(k*x(N)); C(2*N,2*N)=cos(k*x(N));
        else
            C(2*N,2*N-1)=x(N); C(2*N,2*N)=1;
        end
        res=det(C);
        C=zeros(2*N);
    end
        
    function xb = buscar_intervalos(f,a,b,n)
        z = linspace(a,b,n);
        j = 0; 
        y1=f(z(1));
        for m = 1:length(z)-1
            y2=f(z(m+1));
            if sign(y1) ~= sign(y2) 
                j = j + 1;
                xb(j,1) = z(m);
                xb(j,2) = z(m+1);
            end
            y1=y2;
        end
        if isempty(xb) 
            disp('no se han encontrado cambios de signo')
        else
        disp(['número de intervalos:' int2str(j)]) 
        end
    end 

end

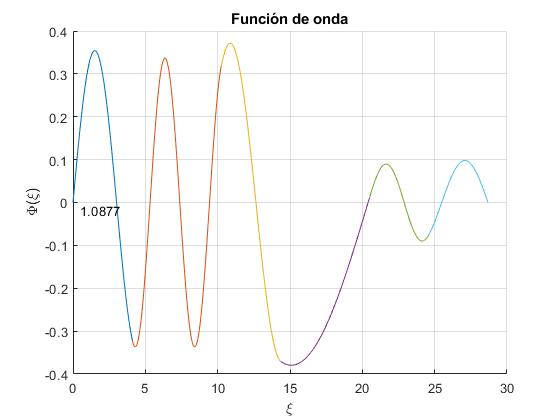
Comprobamos que Ψ(ξ_N)≈0, quitando los comentarios % delante de la porción de código titulada, comprobación

Tomando como referencia este ejemplo, se pueden estudiar otros pozos de potencial V(x) de profundidad infinita, V(0)=∞ y V(x_N)=∞

Referencias

M. A. Doncheski, R. W. Robinett. Comparing classical and quantum probability distributions for an asymmetric infinite well. (1999)

B Cameron Reed. Classroom-suitable matrix method for one-dimensional stepped quantum potentials. Eur. J. Phys. 42 (2021) 065404

Pozo de potencial asimétrico (I)

Niveles de energía

Funciones de onda

Pozo de potencial asimétrico (II)

Energía, E<V0

Energía, E>V0

Funciones de onda

Pozo de potencial doble

Energía, E<V0

Energía, E>V0

Funciones de onda

Una variante del pozo de potencial de profundidad infinita

Niveles de energía

Funciones de onda

Referencias

Energía, E<V₀

Energía, E>V₀

Energía, E<V₀

Energía, E>V₀