La función δ(x-a) de Dirac es nula en todos los puntos excepto en x=a donde es infinito. Tiene las siguientes propiedades

${\displaystyle \begin{array}{l}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\delta (x-a)dx}=1\\ {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f(x)\delta (x-a)dx}=f(a)\end{array}}$

Un pozo de potencial delta de Dirac

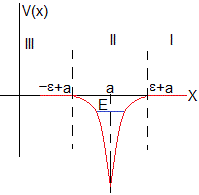
En este apartado, resolveremos la ecuación de Schrödinger para el pozo de potencial delta de Dirac centrado en la posición x=a

${\displaystyle \begin{array}{l}-\frac{{\hslash }^2}{2m}\frac{d^2\psi (x)}{d{x}^2}+V(x)·\psi (x)=E·\psi (x)\\ -\frac{{\hslash }^2}{2m}\frac{d^2\psi (x)}{d{x}^2}-\alpha \frac{{\hslash }^2}{2m}\delta (x-a)·\psi (x)=E·\psi (x)\end{array}}$

Representamos el potencial delta de Dirac por la función que se muestra en la figura, un pozo de anchura 2ε y profundidad que tiende a infinito, siendo ε→0

• Región I, x>ε+a

${\displaystyle \begin{array}{l}\frac{d^2\psi }{d{x}^2}+\frac{2m}{{\hslash }^2}E·\psi =\mathrm{0,}E<0\\ \frac{d^2\psi }{d{x}^2}-k^2·\psi =\mathrm{0,}{k}^2=-\frac{2m}{{\hslash }^2}E\\ {\psi }_I(x)=A\exp (-kx)+B\exp (kx)\end{array}}$

Cuando x se hace grande el segundo término tiende hacia infinito, por lo que B es cero

${\displaystyle {\psi }_I(x)=A\exp (-kx),x>a+\epsilon }$

• Región III, x<-ε+a

${\displaystyle \begin{array}{l}\frac{d^2\psi }{d{x}^2}-k^2·\psi =\mathrm{0,}{k}^2=-\frac{2m}{{\hslash }^2}E\\ {\psi }_{III}(x)=A\exp (-kx)+B\exp (kx)\end{array}}$

cuando x→-∞, el primer término se hace muy grande, por lo que el coeficiente A tendrá que anularse

Niveles de energía

• La función de onda es continua en x=a

Como la región II tiene una achura 2ε infinitamente pequeña, la continuidad de la función de onda se expresa

${\displaystyle \begin{array}{l}{\psi }_I(a)={\psi }_{III}(a)\\ A\exp (-ka)=B\exp (ka)\\ B=A\exp (-2ka)\end{array}}$

• La derivada primera de la función de onda NO es continua en x=a

Integramos la ecuación de Schrödinger en el pequeño intervalo de a-ε, a+ε

${\displaystyle \begin{array}{l}-\frac{{\hslash }^2}{2m}{\displaystyle \underset{a-\epsilon }{\overset{a+\epsilon }{\int }}\frac{d^2\psi (x)}{d{x}^2}}dx-{\displaystyle \underset{a-\epsilon }{\overset{a-\epsilon }{\int }}\alpha \frac{{\hslash }^2}{2m}\delta (x-a)·\psi (x)·dx}=E·{\displaystyle \underset{a-\epsilon }{\overset{a+\epsilon }{\int }}\psi (x)·dx}\\ -\frac{{\hslash }^2}{2m}\underset{\epsilon \to 0}{\lim }\left({\frac{d{\psi }_I(x)}{dx}|}_{a+\epsilon }-{\frac{d{\psi }_{III}(x)}{dx}|}_{a-\epsilon }\right)-\alpha \frac{{\hslash }^2}{2m}\psi (a)=0\end{array}}$

• El primer término, es la integral de la derivada segunda que es la derivada primera, entre los límites especificados

• En el segundo término, utilizamos la propiedad de la función δ(x) delta de Dirac.

• En el segundo miembro, la integral de una función continua entre límites muy próximos es aproximadamente cero

${\displaystyle \begin{array}{l}\underset{\epsilon \to 0}{\lim }\left({-kA{e}^{-kx}|}_{a+\epsilon }-{kA{e}^{-2ka}{e}^{kx}|}_{a-\epsilon }\right)=-\alpha A{e}^{-ka}\\ \underset{\epsilon \to 0}{\lim }\left(-2Ak{e}^{-k(a+\epsilon )}\right)=-\alpha A{e}^{-ka}\\ -2Ak=-\alpha A\\ k=\frac{\alpha }{2}\end{array}}$

La energía del único nivel es

${\displaystyle {\left(\frac{\alpha }{2}\right)}^2=-\frac{2m}{{\hslash }^2}E,E=-\frac{{\hslash }^2{\alpha }^2}{8m}}$

El coeficiente A se calcula de modo que

Función de onda

${\displaystyle \{\begin{array}{l}\psi (x)=A\exp (-kx),x>a\\ \psi (x)=A\exp (-2ka)·\exp (kx),x<a\end{array}}$

Normalizamos la función de onda para determinar el coeficiente A

${\displaystyle \begin{array}{l}{\displaystyle \underset{-\infty }{\overset{a}{\int }}{\left(A\exp (-2ka)·\exp (kx)\right)}^{2}dx+}{\displaystyle \underset{a}{\overset{\infty }{\int }}{\left(A\exp (-kx)\right)}^{2}dx}=1\\ \frac{A^2}{2k}+\frac{A^2}{2k}\exp (-2ka)=\mathrm{1,}{A}^2=\frac{2k}{1+\exp (-2ka)}\end{array}}$

Hay un único estado ligado para el potencial delta de Dirac. La función de onda es simétrica

Representamos la función de onda para un pozo de potencial delta de Dirac de α=2, centrado en la posición a=1

alfa=2;
a=1;
k=alfa/2;
A=sqrt(2*k/(1+exp(-2*k*a)));
B=A*exp(-2*k*a);
hold on
fplot(@(x) B*exp(k*x),[-5,a])
fplot(@(x) A*exp(-k*x),[a,6])
hold off
grid on
xlabel('x')
ylabel('\Phi(x)')
title('Función de onda')

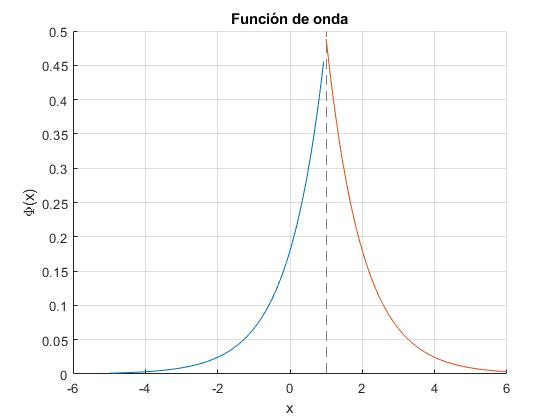
Como apreciamos la función de onda es continua en x=a, pero no lo es su derivada primera

Dos pozos de potencial delta de Dirac

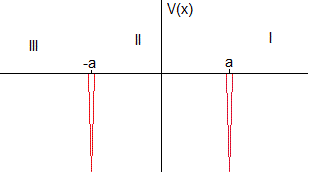
Estudiamos un sistema formado por dos pozos de potencial delta de Dirac centrados en x=-a y x=a

En las tres regiones V(x)=0. La ecuación de Schrödinger se escribe

${\displaystyle \begin{array}{l}\frac{d^2\psi }{d{x}^2}+\frac{2m}{{\hslash }^2}E·\psi =\mathrm{0,}E<0\\ \frac{d^2\psi }{d{x}^2}-k^2·\psi =\mathrm{0,}{k}^2=-\frac{2m}{{\hslash }^2}E\end{array}}$

Las soluciones en cada una de las regiones es

${\displaystyle \{\begin{array}{l}x>a,{\psi }_I(x)=A\exp (-kx)\\ -a<x<a,{\psi }_{II}(x)=C\exp (-kx)+D\exp (kx)\\ x<-a,{\psi }_{III}(x)=B\exp (kx)\end{array}}$

Niveles de energía

Determinamos los niveles de energía,

• La función de onda es continua en x=a

${\displaystyle \{\begin{array}{l}{\psi }_I(a)={\psi }_{II}(a)\\ A\exp (-ka)=C\exp (-ka)+D\exp (ka)\end{array}}$

• La función de onda es continua en x=-a

${\displaystyle \{\begin{array}{l}{\psi }_{III}(-a)={\psi }_{II}(-a)\\ B\exp (-ka)=C\exp (ka)+D\exp (-ka)\end{array}}$

• La derivada primera de la función de onda NO es continua en x=a

Integramos la ecuación de Schrödinger en el pequeño intervalo de a-ε, a+ε

${\displaystyle \begin{array}{l}-\frac{{\hslash }^2}{2m}{\displaystyle \underset{a-\epsilon }{\overset{a+\epsilon }{\int }}\frac{d^2\psi (x)}{d{x}^2}}dx-{\displaystyle \underset{a-\epsilon }{\overset{a-\epsilon }{\int }}\alpha \frac{{\hslash }^2}{2m}\delta (x-a)·\psi (x)·dx}-{\displaystyle \underset{a-\epsilon }{\overset{a-\epsilon }{\int }}\alpha \frac{{\hslash }^2}{2m}\delta (x+a)·\psi (x)·dx}=E·{\displaystyle \underset{a-\epsilon }{\overset{a+\epsilon }{\int }}\psi (x)·dx}\\ -\frac{{\hslash }^2}{2m}\underset{\epsilon \to 0}{\lim }\left({\frac{d{\psi }_I(x)}{dx}|}_{a+\epsilon }-{\frac{d{\psi }_{II}(x)}{dx}|}_{a-\epsilon }\right)-\alpha \frac{{\hslash }^2}{2m}\psi (a)=0\\ \underset{\epsilon \to 0}{\lim }\left({\frac{d{\psi }_I(x)}{dx}|}_{a+\epsilon }-{\frac{d{\psi }_{II}(x)}{dx}|}_{a-\epsilon }\right)=-\alpha \psi (a)\\ \underset{\epsilon \to 0}{\lim }\left(-kA\exp \left(-k(a+\epsilon )\right)+kC\exp \left(-k(a-\epsilon )\right)-kD\exp \left(k(a-\epsilon )\right)\right)=-\alpha A\exp (-ka)\\ -kA\exp \left(-ka\right)+kC\exp \left(-ka\right)-kD\exp \left(ka\right)=-\alpha A\exp (-ka)\\ \left(kC-kA+\alpha A\right)\exp \left(-ka\right)=kD\exp \left(ka\right)\end{array}}$

• La derivada primera de la función de onda NO es continua en x=-a

Integramos la ecuación de Schrödinger en el pequeño intervalo de -a-ε, -a+ε

${\displaystyle \begin{array}{l}-\frac{{\hslash }^2}{2m}{\displaystyle \underset{-a-\epsilon }{\overset{-a+\epsilon }{\int }}\frac{d^2\psi (x)}{d{x}^2}}dx-{\displaystyle \underset{-a-\epsilon }{\overset{-a+\epsilon }{\int }}\alpha \frac{{\hslash }^2}{2m}\delta (x-a)·\psi (x)·dx}-{\displaystyle \underset{-a-\epsilon }{\overset{-a+\epsilon }{\int }}\alpha \frac{{\hslash }^2}{2m}\delta (x+a)·\psi (x)·dx}=E·{\displaystyle \underset{-a-\epsilon }{\overset{-a+\epsilon }{\int }}\psi (x)·dx}\\ -\frac{{\hslash }^2}{2m}\underset{\epsilon \to 0}{\lim }\left({\frac{d{\psi }_{II}(x)}{dx}|}_{-a+\epsilon }-{\frac{d{\psi }_{III}(x)}{dx}|}_{-a-\epsilon }\right)-\alpha \frac{{\hslash }^2}{2m}\psi (-a)=0\\ \underset{\epsilon \to 0}{\lim }\left({\frac{d{\psi }_{II}(x)}{dx}|}_{-a+\epsilon }-{\frac{d{\psi }_{III}(x)}{dx}|}_{-a-\epsilon }\right)=-\alpha \psi (-a)\\ \underset{\epsilon \to 0}{\lim }\left(-kC\exp \left(-k(-a+\epsilon )\right)+kD\exp \left(k(-a+\epsilon )\right)-kB\exp \left(k(-a-\epsilon )\right)\right)=-\alpha B\exp (-ka)\\ -kC\exp \left(ka\right)+kD\exp \left(-ka\right)-kB\exp \left(-ka\right)=-\alpha B\exp (-ka)\\ \left(kD-kB+\alpha B\right)\exp \left(-ka\right)=kC\exp \left(ka\right)\end{array}}$

El sistema de cuatro ecuaciones es

${\displaystyle \{\begin{array}{l}A=C+D\exp (2ka)\\ B=D+C\exp (2ka)\\ kC-kA+\alpha A=kD\exp (2ka)\\ kD-kB+\alpha B=kC\exp (2ka)\end{array}}$

La solución es

${\displaystyle \begin{array}{l}\{\begin{array}{l}\left(\alpha -2k\right)\exp (2ka)D+\alpha C=0\\ \alpha D+\left(\alpha -2k\right)\exp (2ka)C=0\end{array}\\ {\left(\alpha -2k\right)}^2\exp (4ka)-{\alpha }^2=0\\ \alpha -2k=\pm \alpha \exp (-2ka)\\ k=\frac{\alpha }{2}\left(1\pm \exp (-2ka)\right)\end{array}}$

Llamando a la incógnita x=k. Buscamos la solución de las dos ecuaciones transcendentes

${\displaystyle e^{-2ax}=\frac{2}{\alpha }x-\mathrm{1,}{e}^{-2ax}=-\frac{2}{\alpha }x+1}$

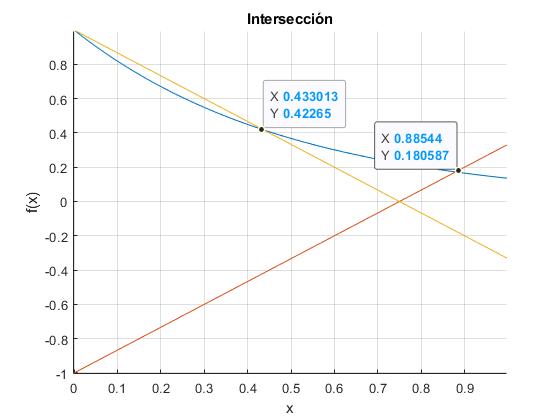
Solución gráfica aproximada

Dibujamos la función exponencial y=exp(-2ax), la recta y=2x/α-1 y la recta y=-2x/α+1

La intersección entre las rectas y la exponencial nos proporciona las soluciones k₊ y k_- de las dos ecuaciones transcendentes

alfa=1.5;
a=1;
hold on
fplot(@(x) exp(-2*a*x), [0,1])
fplot(@(x) 2*x/alfa-1, [0,1])
fplot(@(x) 1-2*x/alfa, [0,1])
hold off
grid on
xlabel('x')
ylabel('f(x)')
title('Intersección')

%soluciones exactas
k1=lambertw(0,a*alfa*exp(-a*alfa))/(2*a)+alfa/2;
k2=lambertw(0,-a*alfa*exp(-a*alfa))/(2*a)+alfa/2;
disp([k1,k2])

Las soluciones exactas (véase más abajo) son

  0.8792    0.4371

Disminuimos el valor del parámetro α≤1, la intersección entre la recta y=-2x/α+1 y la exponencial y=exp(-2ax) es el punto (0,1). Un nivel de energía es E=0. Por ejemplo, cambiamos el valor de la variable alfa=0.9, obtenemos

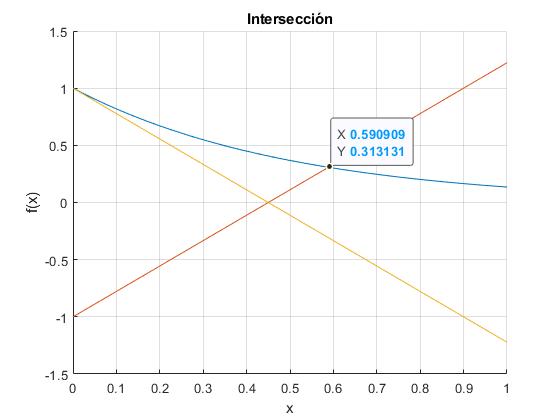
0.5886   -0.0000

Solución exacta

Las dos ecuaciones implícitas se puede convertir en explícitas utilizando la función W de Lambert

${\displaystyle \begin{array}{l}{a}^{bx+c}=dx+f\\ x=\frac{-1}{b\ln a}W\left(\frac{-b}{d}(\ln a)a^{c-bf/d}\right)-\frac{f}{d}\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}{k}_{+}=\frac{1}{2a}W\left(a\alpha \exp \left(-a\alpha \right)\right)+\frac{\alpha }{2}\\ k_{-}=\frac{1}{2a}W\left(-a\alpha \exp \left(-a\alpha \right)\right)+\frac{\alpha }{2}\end{array}}$

Funciones de onda

${\displaystyle \{\begin{array}{l}x>a,{\psi }_I(x)=A\exp (-kx)\\ -a<x<a,{\psi }_{II}(x)=C\exp (-kx)+D\exp (kx)\\ x<-a,{\psi }_{III}(x)=B\exp (kx)\end{array}}$

Calculamos el coeficiente A de modo que

${\displaystyle {\displaystyle \underset{-\infty }{\overset{-a}{\int }}{\left|{\psi }_{III}(x)\right|}^{2}dx}+{\displaystyle \underset{-a}{\overset{a}{\int }}{\left|{\psi }_{II}(x)\right|}^{2}dx+{\displaystyle \underset{a}{\overset{\infty }{\int }}{\left|{\psi }_I(x)\right|}^{2}dx=1}}}$

es decir,

${\displaystyle \begin{array}{l}{\displaystyle \underset{-\infty }{\overset{-a}{\int }}{B}^2\exp \left(2kx\right)}dx+{\displaystyle \underset{-a}{\overset{a}{\int }}{\left(C\exp (-kx)+D\exp (kx)\right)}^{2}dx+{\displaystyle \underset{a}{\overset{\infty }{\int }}{A}^2\exp (-2kx)dx}}=1\\ \left(A^2+B^2\right)\frac{e^{-2ka}}{2k}+\left(\frac{e^{2ka}-e^{-2ka}}{2k}\right)\left(C^2+D^2\right)+4CDa=1\end{array}}$

• La solución k₊

${\displaystyle k=\frac{\alpha }{2}\left(1+\exp (-2ka)\right)}$

implica que, C=D, A=B, tenemos una función de onda simétrica. El coeficiente C vale

${\displaystyle C=\frac{1}{1+e^{2ka}}A}$

El coeficiente A vale

${\displaystyle \begin{array}{l}{A}^2\left\{\frac{e^{-2k_{+}a}}{k_{+}}+\left(\frac{e^{2k_{+}a}-e^{-2k_{+}a}}{k_{+}}\right)\frac{1}{{\left(1+e^{2k_{+}a}\right)}^2}+4a\frac{1}{{\left(1+e^{2k_{+}a}\right)}^2}\right\}=1\\ A^2\frac{e^{2k_{+}a}+2k_{+}a+1}{k_{+}{\left(1+e^{2k_{+}a}\right)}^2}=\frac{1}{2}\end{array}}$

• La solución k_-

${\displaystyle k=\frac{\alpha }{2}\left(1-\exp (-2ka)\right)}$

implica que, C=-D, A=-B, tenemos una función de onda antisimétrica

El coeficiente C vale

${\displaystyle C=\frac{1}{1-e^{2ka}}A}$

El coeficiente A vale

${\displaystyle \begin{array}{l}{A}^2\left\{\frac{e^{-2k_{-}a}}{k_{-}}+\left(\frac{e^{2k_{-}a}-e^{-2k_{-}a}}{k_{-}}\right)\frac{1}{{\left(1-e^{2k_{-}a}\right)}^2}-4a\frac{1}{{\left(1-e^{2k_{-}a}\right)}^2}\right\}=1\\ A^2\frac{e^{2k_{-}a}-2k_{-}a-1}{k_{-}{\left(1-e^{2k_{-}a}\right)}^2}=\frac{1}{2}\end{array}}$

Sea el sistema de dos pozos de potencial delta de Dirac centrados en x=-1, y x=1. Asignamos al parámetro α=2. Calculamos, utilizando la función lambertw de MATLAB, k₊ y k_-. Representamos las funciones de onda de simétricas y antisimétricas

a=1;
alfa=2;
k1=lambertw(0,a*alfa*exp(-a*alfa))/(2*a)+alfa/2;
k2=lambertw(0,-a*alfa*exp(-a*alfa))/(2*a)+alfa/2;

hold on
%simétricas
A=(1+exp(2*k1*a))*sqrt(k1/(2*(exp(2*k1*a)+2*k1*a+1)));
C=A/(1+exp(2*k1*a));
fplot(@(x) A*exp(-k1*x),[a,5*a], 'color','r')
fplot(@(x) C*exp(-k1*x)+C*exp(k1*x), [-a,a], 'color','r')
fplot(@(x) A*exp(k1*x),[-5*a,-a], 'color','r')

%antisimétricas
A=(1-exp(2*k2*a))*sqrt(k2/(2*(exp(2*k2*a)-2*k2*a-1)));
C=A/(1-exp(2*k2*a));
fplot(@(x) A*exp(-k2*x),[a,5*a], 'color','b')
fplot(@(x) C*exp(-k2*x)-C*exp(k2*x), [-a,a], 'color','b')
fplot(@(x) -A*exp(k2*x),[-5*a,-a], 'color','b')
hold off
grid on
xlabel('x')
ylabel('\Phi(x)')
title('Funciones de onda')

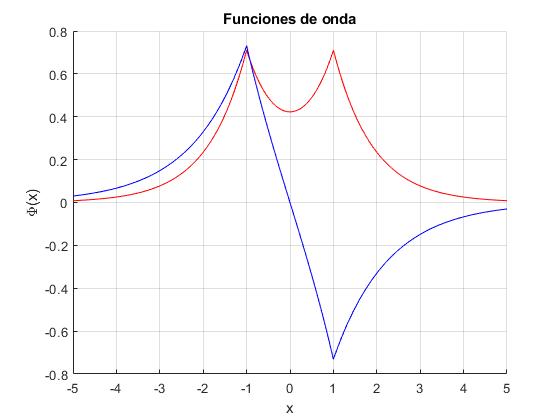
>> k1,k2
k1 =    1.1089
k2 =    0.7968

La función de onda de simétrica corresponde al nivel fundamental, la energía (negativa) más baja, k1 en el código

${\displaystyle k^2=-\frac{2m}{{\hslash }^2}E}$

Referencias

The Delta-Function Potential

Armando Martínez Téllez. El potencial delta de Dirac