Potencial delta de Dirac

En este apartado, resolveremos la ecuación de Schrödinger para un pozo de potencial delta de Dirac centrado en el origen, cuando la energía de la partícula E>0

${\displaystyle \begin{array}{l}-\frac{{\hslash }^2}{2m}\frac{d^2\psi (x)}{d{x}^2}+V(x)·\psi (x)=E·\psi (x)\\ V(x)=-\alpha \frac{{\hslash }^2}{2m}\delta (x)\end{array}}$

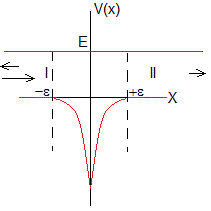
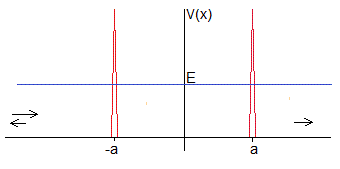
Representamos el potencial delta de Dirac por la función que se muestra en la figura, un pozo de anchura 2ε y profundidad que tiende a infinito, siendo ε→0

• Región I, x<0

${\displaystyle \begin{array}{l}\frac{d^2\psi }{d{x}^2}+k^2·\psi =\mathrm{0,}{k}^2=\frac{2m}{{\hslash }^2}E\\ {\psi }_I(x)=A\exp (-ikx)+B\exp (ikx)\end{array}}$

• Región II, x>0

${\displaystyle \begin{array}{l}\frac{d^2\psi }{d{x}^2}+k^2·\psi =0\\ {\psi }_{II}(x)=C\exp (ikx)\end{array}}$

No hay partículas que se muevan desde la derecha hacia la izquierda en la región III, el término Dexp(-ikx) no está presente

Ahora, vamos a determinar los coeficientes B, C, en función de A, para lo que se precisan dos ecuaciones

• La función de onda es continua en x=0

Como la región II tiene una anchura 2ε infinitamente pequeña

${\displaystyle \begin{array}{l}{\psi }_I(0)={\psi }_{II}(0)\\ A+B=C\end{array}}$

• La derivada primera de la función de onda NO es continua en x=0

Integramos la ecuación de Schrödinger en el pequeño intervalo de -ε a +ε

${\displaystyle \begin{array}{l}-\frac{{\hslash }^2}{2m}{\displaystyle \underset{-\epsilon }{\overset{\epsilon }{\int }}\frac{d^2\psi (x)}{d{x}^2}}dx-{\displaystyle \underset{-\epsilon }{\overset{\epsilon }{\int }}\alpha \frac{{\hslash }^2}{2m}\delta (x)·\psi (x)·dx}=E·{\displaystyle \underset{-\epsilon }{\overset{\epsilon }{\int }}\psi (x)·dx}\\ -\frac{{\hslash }^2}{2m}\underset{\epsilon \to 0}{\lim }\left({\frac{d{\psi }_{II}(x)}{dx}|}_{\epsilon }-{\frac{d{\psi }_I(x)}{dx}|}_{-\epsilon }\right)-\alpha \frac{{\hslash }^2}{2m}{\psi }_{II}(0)=0\end{array}}$

• El primer término, es la integral de la derivada segunda que es la derivada primera, entre los límites especificados

• En el segundo término, utilizamos la propiedad de la función δ(x) delta de Dirac,

• En el segundo miembro, la integral de una función continua entre límites muy próximos es aproximadamente cero

${\displaystyle \begin{array}{l}\underset{\epsilon \to 0}{\lim }\left({ikC{e}^{ikx}|}_{\epsilon }-{\left(ikA{e}^{ikx}-ikB{e}^{-ikx}\right)|}_{-\epsilon }\right)=-\alpha C\\ \underset{\epsilon \to 0}{\lim }\left(ikC{e}^{ik\epsilon }-ikA{e}^{-ik\epsilon }+ikB{e}^{ik\epsilon }\right)=-\alpha C\\ ikC-ikA+ikB=-\alpha C\end{array}}$

Resolvemos el sistema de dos ecuaciones

${\displaystyle \begin{array}{l}\{\begin{array}{l}A+B=C\\ C-A+B=-\frac{\alpha }{ik}C\end{array}\\ C=\frac{2ik}{\alpha +2ik}A,B=\frac{-\alpha }{\alpha +2ik}A\end{array}}$

Los coeficientes de reflexión R y transmisión T son

${\displaystyle \begin{array}{l}R={\left|\frac{B}{A}\right|}^2=\frac{{\alpha }^2}{{\alpha }^2+4k^2}\\ T={\left|\frac{C}{A}\right|}^2=\frac{4k^2}{{\alpha }^2+4k^2}\end{array}}$

Comprobamos que R+T=1

El cambio de un pozo de potencial delta de Dirac a una barrera, α por -α no modifica el coeficiente de transmisión T

Representamos el coeficiente T en función de la energía E, para α=2

alfa=2;
ee=linspace(0,10,100);
T=zeros(1,length(ee));
i=1;
for E=ee
    k=sqrt(E);
   T(i)=4*k^2/(alfa^2+4*k^2);
   i=i+1;
end
plot(ee,T)
grid on
xlabel('E')
ylabel('T')
title('Coeficiente de transmisión')

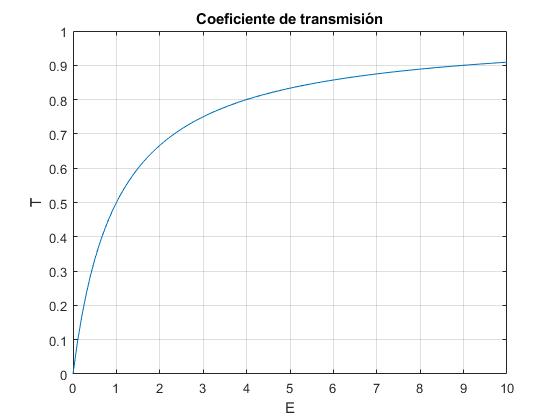
A medida que la energía E o k se incrementa, el coeficiente T tiende a la unidad

Comprobamos que la derivada primera de la función de onda es discontinua en x=0

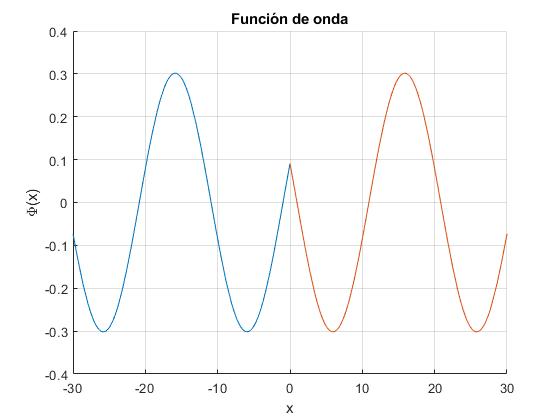
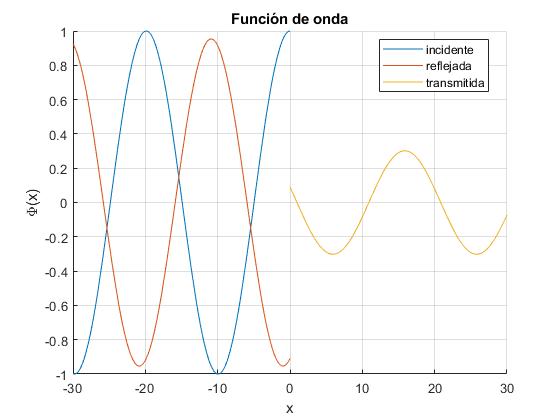
Representamos la función de onda en las dos regiones I (x<0) y II (x>0), para la energía E=0.1 y α=2

E=0.1;
k=sqrt(E);
alfa=2;

A=1;
B=-alfa*A/(alfa+2*1i*k);
C=2*1i*k*A/(alfa+2*1i*k);
hold on
fplot(@(x) real(A*exp(1i*k*x)+B*exp(-1i*k*x)),[-30,0]) %incidente+reflejada
%fplot(@(x) real(A*exp(1i*k*x)),[-30,0]) %incidente
%fplot(@(x) real(B*exp(-1i*k*x)),[-30,0]) %relejada
fplot(@(x) real(C*exp(1i*k*x)),[0,30]) %transmitida
hold off
grid on
xlabel('x')
ylabel('\Phi(x)')
title('Función de onda')

Separamos la parte incidente de la función de onda en I de la reflejada

Barrera de potencial

El cambio de un pozo de potencial delta de Dirac por una una barrera, -α por α, no modifica el coeficiente de transmisión T

Dos pozos de potencial delta de Dirac

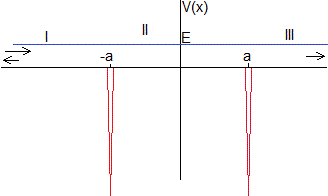
Consideremos dos pozos de potencial delta de Dirac centrados en -a y +a

${\displaystyle V(x)=-\alpha \frac{{\hslash }^2}{2m}\left(\delta (x+a)+\delta (x-a)\right)}$

Dividimos el eje X en tres regiones. -∞<x<-a, -a<x<a, a<x<∞

La solución de la ecuación de Schrödinger en las tres regiones es

${\displaystyle \begin{array}{l}\frac{d^2\psi }{d{x}^2}+\frac{2m}{{\hslash }^2}E·\psi =\mathrm{0,}E>0\\ \frac{d^2\psi }{d{x}^2}+k^2·\psi =\mathrm{0,}{k}^2=\frac{2m}{{\hslash }^2}E\\ \{\begin{array}{l}x<-a,{\psi }_I(x)=A\exp (ikx)+B\exp (-ikx)\\ -a<x<a,{\psi }_{II}(x)=C\exp (ikx)+D\exp (-ikx)\\ x>a,{\psi }_{III}(x)=F\exp (ikx)\end{array}\end{array}}$

No hay partículas que se muevan desde la derecha hacia la izquierda en la región III, el término Gexp(-ikx) no está presente

Ahora, vamos a determinar los coeficientes B, C, D y F en función de A, para lo que se precisan cuatro ecuaciones

• Continuidad de la función de onda en x=-a

${\displaystyle \{\begin{array}{l}{\psi }_I(-a)={\psi }_{II}(-a)\\ A\exp (-ika)+B\exp (ika)=C\exp (-ika)+D\exp (ika)\end{array}}$

• Continuidad de la función de onda en x=a

${\displaystyle \{\begin{array}{l}{\psi }_{II}(a)={\psi }_{III}(a)\\ C\exp (ika)+D\exp (-ika)=F\exp (ika)\end{array}}$

• La derivada primera de la función de onda es discontinua en x=-a

Integramos la ecuación de Schrödinger en el pequeño intervalo de -a-ε a -a+ε

${\displaystyle \begin{array}{l}-\frac{{\hslash }^2}{2m}{\displaystyle \underset{-a-\epsilon }{\overset{-a+\epsilon }{\int }}\frac{d^2\psi (x)}{d{x}^2}}dx-{\displaystyle \underset{-a-\epsilon }{\overset{-a+\epsilon }{\int }}\alpha \frac{{\hslash }^2}{2m}\delta (x-a)·\psi (x)·dx}-{\displaystyle \underset{-a-\epsilon }{\overset{-a+\epsilon }{\int }}\alpha \frac{{\hslash }^2}{2m}\delta (x+a)·\psi (x)·dx}=E·{\displaystyle \underset{-a-\epsilon }{\overset{-a+\epsilon }{\int }}\psi (x)·dx}\\ -\frac{{\hslash }^2}{2m}\underset{\epsilon \to 0}{\lim }\left({\frac{d{\psi }_{II}(x)}{dx}|}_{-a+\epsilon }-{\frac{d{\psi }_I(x)}{dx}|}_{-a-\epsilon }\right)-\alpha \frac{{\hslash }^2}{2m}{\psi }_I(-a)=0\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}\underset{\epsilon \to 0}{\lim }\left({\frac{d{\psi }_{II}(x)}{dx}|}_{-a+\epsilon }-{\frac{d{\psi }_I(x)}{dx}|}_{-a-\epsilon }\right)=-\alpha {\psi }_I(-a)\\ \underset{\epsilon \to 0}{\lim }\left(ikC\exp \left(ik(-a+\epsilon )\right)-ikD\exp \left(-ik(-a+\epsilon )\right)-\left(ikA\exp \left(ik(-a+\epsilon )\right)-ikB\exp \left(-ik(-a+\epsilon )\right)\right)\right)=\\ -\alpha \left(A\exp (-ika)+B\exp (ika)\right)\\ ik\left(C\exp \left(-ika\right)-D\exp \left(ika\right)-A\exp \left(-ika\right)+B\exp \left(ika\right)\right)=-\alpha \left(A\exp (-ika)+B\exp (ika)\right)\end{array}}$

• La derivada primera de la función de onda es discontinua en x=a

Integramos la ecuación de Schrödinger en el pequeño intervalo de a-ε a a+ε

${\displaystyle \begin{array}{l}-\frac{{\hslash }^2}{2m}{\displaystyle \underset{a-\epsilon }{\overset{a+\epsilon }{\int }}\frac{d^2\psi (x)}{d{x}^2}}dx-{\displaystyle \underset{a-\epsilon }{\overset{a-\epsilon }{\int }}\alpha \frac{{\hslash }^2}{2m}\delta (x-a)·\psi (x)·dx}-{\displaystyle \underset{a-\epsilon }{\overset{a-\epsilon }{\int }}\alpha \frac{{\hslash }^2}{2m}\delta (x+a)·\psi (x)·dx}=E·{\displaystyle \underset{a-\epsilon }{\overset{a+\epsilon }{\int }}\psi (x)·dx}\\ -\frac{{\hslash }^2}{2m}\underset{\epsilon \to 0}{\lim }\left({\frac{d{\psi }_{III}(x)}{dx}|}_{a+\epsilon }-{\frac{d{\psi }_{II}(x)}{dx}|}_{a-\epsilon }\right)-\alpha \frac{{\hslash }^2}{2m}{\psi }_{III}(a)=0\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}\underset{\epsilon \to 0}{\lim }\left({\frac{d{\psi }_{III}(x)}{dx}|}_{a+\epsilon }-{\frac{d{\psi }_{II}(x)}{dx}|}_{a-\epsilon }\right)=-\alpha {\psi }_{III}(a)\\ \underset{\epsilon \to 0}{\lim }\left(ikF\exp \left(ik(a+\epsilon )\right)-\left(ikC\exp \left(ik(a-\epsilon )\right)-ikD\exp \left(-ik(a-\epsilon )\right)\right)\right)=-\alpha F\exp (ika)\\ ik\left(F\exp \left(ika\right)-C\exp \left(ika\right)+D\exp \left(-ika\right)\right)=-\alpha F\exp (ika)\end{array}}$

Obtenemos un sistema de cuatro ecuaciones

${\displaystyle \{\begin{array}{l}A\exp (-ika)+B\exp (ika)=C\exp (-ika)+D\exp (ika)\\ C\exp (ika)+D\exp (-ika)=F\exp (ika)\\ ik\left(C\exp \left(-ika\right)-D\exp \left(ika\right)-A\exp \left(-ika\right)+B\exp \left(ika\right)\right)=-\alpha \left(A\exp (-ika)+B\exp (ika)\right)\\ ik\left(F\exp \left(ika\right)-C\exp \left(ika\right)+D\exp \left(-ika\right)\right)=-\alpha F\exp (ika)\end{array}}$

Resolvemos el sistema de cuatro ecuaciones con cuatro incógnitas, B, C, D, y F

• Despejamos el coeficiente D de las dos primeras ecuaciones

${\displaystyle \begin{array}{l}\{\begin{array}{l}A+B\exp (2ika)=C+D\exp (2ika)\\ F=C+D\exp (-2ika)=\end{array}\\ D=\frac{A+B\exp (2ika)-F}{2i\sin (2ka)}\end{array}}$

• Despejamos el coeficiente C de las dos primeras ecuaciones

${\displaystyle \begin{array}{l}\{\begin{array}{l}A\exp (-2ika)+B=C\exp (-2ika)+D\\ F\exp (2ika)=C\exp (2ika)+D\end{array}\\ C=-\frac{A\exp (-2ika)+B-F\exp (2ika)}{2i\sin (2ka)}\end{array}}$

• Despejamos el coeficiente D de las dos últimas ecuaciones

${\displaystyle \begin{array}{l}\{\begin{array}{l}ikC-ikD\exp \left(2ika\right)=\left(-\alpha +ik\right)A-\left(\alpha +ik\right)B\exp \left(2ika\right)\\ -ikC+ikD\exp \left(-2ika\right)=-\left(\alpha +ik\right)F\end{array}\\ D=\frac{\left(-\alpha +ik\right)A-\left(\alpha +ik\right)B\exp \left(2ika\right)-\left(\alpha +ik\right)F}{2k\sin (2ka)}\end{array}}$

• Despejamos el coeficiente C de las dos últimas ecuaciones

${\displaystyle \begin{array}{l}\{\begin{array}{l}ikC\exp \left(-2ika\right)-ikD=\left(-\alpha +ik\right)A\exp \left(-2ika\right)-\left(\alpha +ik\right)B\\ -ikC\exp \left(2ika\right)+ikD=-\left(\alpha +ik\right)F\exp \left(2ika\right)\end{array}\\ 2k\sin (2ka)C=\left(-\alpha +ik\right)A\exp \left(-2ika\right)-\left(\alpha +ik\right)B-\left(\alpha +ik\right)F\exp \left(2ika\right)\end{array}}$

El sistema queda reducido a dos ecuaciones

${\displaystyle \{\begin{array}{l}\left(2ik+\alpha \right)F+\alpha \exp (2ika)B=\left(2ik-\alpha \right)A\\ \alpha \exp (2ika)F+\left(2ik+\alpha \right)B=-\alpha \exp (2ika)A\end{array}}$

Despejamos las incógnitas F y B

${\displaystyle \begin{array}{l}F=\frac{4k^2}{{\alpha }^2\exp (4ika)-{\left(2ik+\alpha \right)}^2}A=\frac{4k^2}{{\alpha }^2\left(\exp (4ika)-1\right)+4k\left(k-i\alpha \right)}A\\ B=2i\alpha \frac{2k\cos (2ka)-\alpha \sin (2ka)}{{\alpha }^2\left(\exp (4ika)-1\right)+4k\left(k-i\alpha \right)}A\end{array}}$

El coeficiente transmisión T es

${\displaystyle T={\left|\frac{F}{A}\right|}^2=\frac{8k^4}{{\alpha }^4+8k^4+4k^2{\alpha }^2+{\alpha }^2\left(4k^2-{\alpha }^2\right)\cos (4ka)-4k{\alpha }^3\sin (4ka)}}$

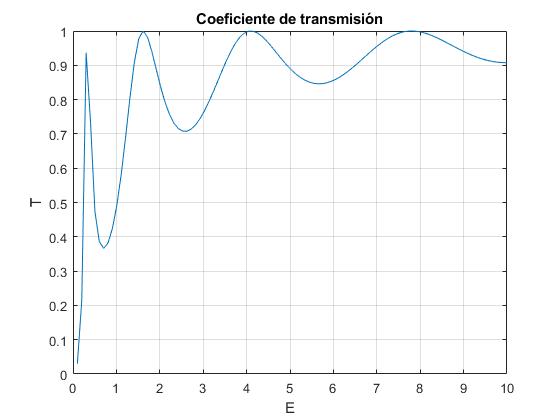
Representamos el coeficiente de transmisión T en función de la energía E para el sistema formado por dos pozos delta de Dirac centrados en x=-2 y x=2 (a=2), el parámetro α=1

alfa=1;
a=2;
ee=linspace(0,10,100);
T=zeros(1,length(ee));
i=1;
for E=ee
    k=sqrt(E);
    T(i)=8*k^4/(alfa^4+8*k^4+4*k^2*alfa^2+alfa^2*(4*k^2-alfa^2)*cos(4*k*a)
-4*k*alfa^3*sin(4*k*a));
    %F=4*k^2/(alfa^2*(exp(4*1i*k*a)-1)+4*k*(k-1i*alfa));
    %T(i)=abs(F)^2;
    i=i+1;
end
plot(ee,T)
grid on
xlabel('E')
ylabel('T')
title('Coeficiente de transmisión')

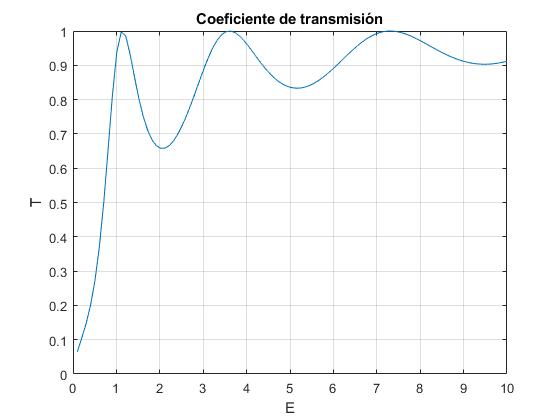
Apreciamos que hay valores de la energía E para los cuales T=1, alcanza su valor máximo

Comprobamos que la derivada primera de la función de onda es discontinua en x=-a y x=a

Representamos la función de onda en las tres regiones I (x<-a), II (-a<x<a) y III (x>a) para la energía E=0.5 y α=1

alfa=1;
a=2;
E=0.5;
k=sqrt(E);
A=1;
F=4*k^2/(alfa^2*(exp(4*1i*k*a)-1)+4*k*(k-1i*alfa));
B=2*1i*alfa*(2*k*cos(2*k*a)-alfa*sin(2*k*a))/
(alfa^2*(exp(4*1i*k*a)-1)+4*k*(k-1i*alfa));
D=(A+B*exp(2*1i*k*a)-F)/(2*1i*sin(2*k*a));
C=1i*(A*exp(-2*1i*k*a)+B-F*exp(2*1i*k*a))/(2*sin(2*k*a));
hold on
fplot(@(x) real(A*exp(1i*k*x)+B*exp(-1i*k*x)), [-10*a,-a]) %incidente+relejada
%fplot(@(x) real(A*exp(1i*k*x)), [-10*a,-a]) %incidente
%fplot(@(x) real(B*exp(-1i*k*x)), [-10*a,-a]) %reflejada
fplot(@(x) real(C*exp(1i*k*x)+D*exp(-1i*k*x)), [-a,a])
fplot(@(x) real(F*exp(1i*k*x)), [a,10*a]) %transmitida
hold off
grid on
xlabel('x')
ylabel('\Phi(x)')
title('Función de onda')

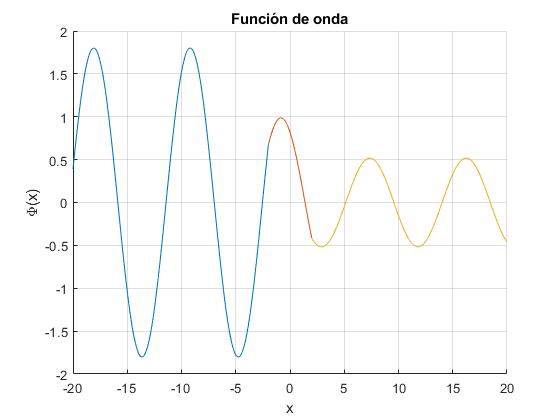
Se muestra la función de onda, en la región I (color azul), II (color rojo) y III (color amarillo)

Separamos la parte incidente de la función de onda de la reflejada, en la región I

Dos barreras de potencial

Cambiando el parámetro -α por α modifica el coeficiente de transmisión T (último término del denominador en α³)

alfa=-1;
a=2;
ee=linspace(0,10,100);
T=zeros(1,length(ee));
i=1;
for E=ee
    k=sqrt(E);
    T(i)=8*k^4/(alfa^4+8*k^4+4*k^2*alfa^2+alfa^2*(4*k^2-alfa^2)*cos(4*k*a)
-4*k*alfa^3*sin(4*k*a));
    i=i+1;
end
plot(ee,T)
grid on
xlabel('E')
ylabel('T')
title('Coeficiente de transmisión')

Referencias

Class 9: The delta function potential

DOUBLE DELTA FUNCTION WELL - SCATTERING STATES