Dinámica de rotación y balance energético
Se utiliza un dispositivo similar a una rueda de bicicleta que puede girar alrededor de un eje fijo. Se enrollan cuerdas de las que penden una o dos pesas tal como se muestra en la figura.
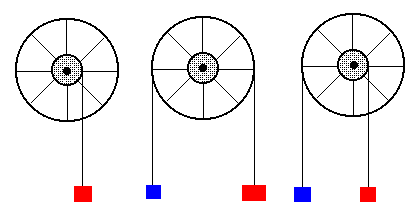
Se mide el tiempo que tarda una pesa en recorrer una determinada altura, partiendo del reposo. A partir de este dato, de las masas de los cuerpos, y de los radios interior y exterior de la rueda, se calcula el momento de inercia por dos procedimientos
- Aplicando las ecuaciones de la dinámica
- Aplicando el principio de conservación de la energía
Primera experiencia
-
Método: conservación de la energía
La comparación de la situación inicial y la situación final nos permite formular rápidamente el principio de conservación de la energía.
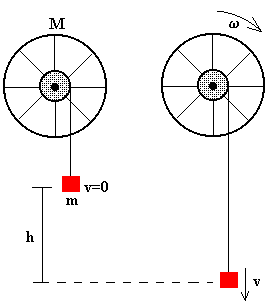
- La pesa de masa m desciende una altura h.
- La pesa de masa m incrementa su velocidad en v
- La rueda gira con velocidad angular ω
La energía potencial disminuye en mgh, su energía cinética se incrementa en mv2/2 y lo mismo ocurre para sólido en rotación, su energía cinética se incrementa en Iω 2/2.
La ecuación del balance energético es
La velocidad v se calcula a partir de h y del tiempo t que tarda la pesa en descender esta altura, partiendo del reposo.
La velocidad angular ω está relacionada con la velocidad v de la pesa que a su vez, es la misma que la velocidad de un punto del borde de la rueda de radio r (siendo r el radio interior de la rueda). Véase la relación entre magnitudes lineales y angulares.
Se completa la siguiente tabla y se despeja el momento de inercia desconocido
| Altura h | |
| Tiempo t | |
| Velocidad v | |
| Radio r | |
| Velocidad angular ω | |
| Masa m de la pesa | |
| Momento de inercia I |
|---|
-
Método: dinámica
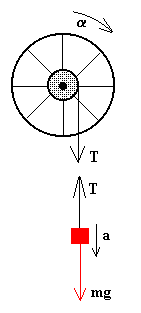
En la figura, se han dibujado el esquema de las fuerzas sobre los cuerpos que intervienen en el movimiento.
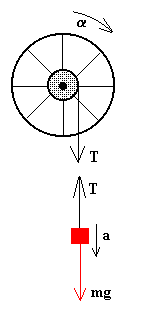
- La ecuación de la dinámica de rotación de la rueda es
- La ecuación de la dinámica de traslación de la pesa es
- La relación entre la aceleración angular α del disco y la aceleración a de la pesa es la misma que la existente entre sus respectivas velocidades
T·r=Iα
mg-T=ma
a=α·r
Conocido el tiempo t que tarda en caer la pesa y la altura h desde la que cae, se determina la aceleración a
A partir de la medida del radio r de la rueda (interior o exterior, según el caso), se calcula la aceleración angular α del disco, la tensión T de la cuerda y se despeja el momento de inercia I desconocido.
| Altura h | |
| Tiempo t | |
| Aceleración a | |
| Radio r | |
| Aceleración angular α | |
| Masa de la pesa m | |
| Tensión de la cuerda T | |
| Momento de inercia I |
|---|
Por ejemplo, se introduce
- Masa de la primera pesa cero (m1=0),
- Masa de la segunda pesa m2=200 g,
- Radio interior r=30 cm.
Se pulsa el botón titulado Nuevo y se mide el tiempo que tarda la pesa en recorrer una determinada altura. Se pulsa el botón titulado Ⅱ para detener el movimiento a la altura deseada. Se calcula el momento de inercia.
Segunda experiencia
-
Método: conservación de la energía
La comparación de la situación inicial y la situación final nos permite formular el principio de conservación de la energía.
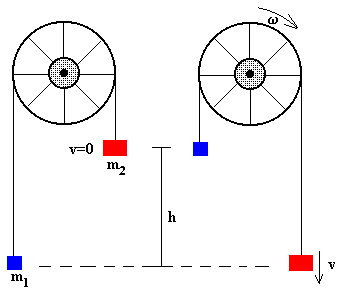
- La pesa de masa m2 desciende una altura h.
- La pesa de masa m1 asciende la misma altura h.
- La pesa de masa m1 aumenta en v su velocidad.
- Lo mismo le ocurre a la pesa de masa m2
- La rueda gira con velocidad angular ω .
Se formula el principio de conservación de la energía
Calculando la velocidad v a partir de h y del tiempo t que la pesa tarda en descender esta altura, partiendo del reposo, y relacionando v con velocidad angular ω de la rueda, se obtiene el momento de inercia I.
Se completa la siguiente tabla y se despeja el momento de inercia desconocido
| Altura h | |
| Tiempo t | |
| Velocidad v | |
| Radio R | |
| Velocidad angular ω | |
| Masa m1 de la pesa 1 | |
| Masa m2 de la pesa 2 | |
| Momento de inercia I |
|---|
-
Método: Dinámica
En la figura, se han dibujado el esquema de las fuerzas sobre los cuerpos que intervienen en el movimiento. A partir de este esquema, formulamos las ecuaciones de la dinámica de cada uno de los cuerpos.
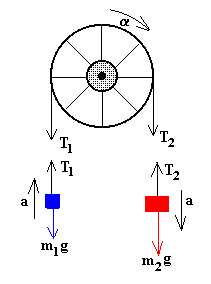
m2g-T2=m2a
T1-m1g=m1a
T2R-T1R=Iα
a=αR
Como en el ejemplo anterior, conocido el tiempo t que tarda en caer la pesa de mayor masa y la altura h desde la que cae, se determina la aceleración a
A partir de la medida del radio exterior R de la rueda, se calcula la aceleración angular α del disco, las tensiones T1 y T2 de la cuerda y se despeja el momento de inercia I desconocido.
| Altura h | |
| Tiempo t | |
| Aceleración a | |
| Radio R | |
| Aceleración angular α | |
| Masa m1 de la pesa 1 | |
| Masa m2 de la pesa 2 | |
| Tensión de la cuerda T1 | |
| Tensión de la cuerda T2 | |
| Momento de inercia I |
|---|
Ejemplo, se introduce:
- Masa m1 de la primera pesa, 100 g
- Masa m2 de la segunda pesa, 200 g
- Radio R, 30 cm.
Se pulsa el botón titulado Nuevo y se mide el tiempo que tarda la pesa en recorrer una determinada altura. Se pulsa el boón titulado Ⅱ para detener el movimiento a una determinada altura. Se calcula el momento de inercia
Tercera experiencia
-
Método: conservación de la energía
Comparando el estado inicial y final observamos que
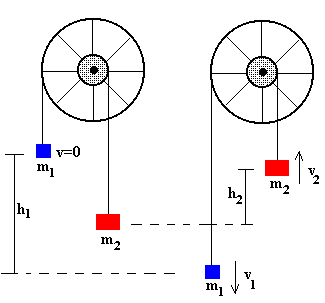
- La pesa de masa m1 desciende una altura h1
- La pesa de masa m2 asciende una altura h2
- La pesa de masa m1 incrementa su velocidad en v1
- La pesa de masa m2 incrementa su velocidad en v2
- La rueda está girando con velocidad ω
Formulamos el principio de conservación de la energía
Existe una relación entre h1 y h2, la misma que existe entre v1 y v2. Recordaremos que las magnitudes angulares son las mismas para todos los puntos del sólido en rotación mientras que las magnitudes lineales son proporcionales al radio.
- v1=ω·r1
- v2=ω·r2
- h1=θ·r1
- h2=θ·r2
ω es la velocidad angular de la rueda y θ es el ángulo girado en el tiempo t.
Dados los datos de h1, la altura que cae la pesa de masa m1 y el tiempo t que tarda en caer,
y a partir de las medidas de los radios interior r2 y exterior r1 de la rueda calculamos, el momento de inercia I desconocido de la rueda, siguiendo los mismos pasos que en los ejercicios previos.
Se completa la siguiente tabla y se despeja el momento de inercia desconocido
| Altura h1 | |
| Radio r1 | |
| Radio r2 | |
| Altura h2 | |
| Tiempo t | |
| Velocidad v1 | |
| Velocidad angular ω | |
| Velocidad v2 | |
| Masa m1 de la pesa 1 | |
| Masa m2 de la pesa 2 | |
| Momento de inercia I |
|---|
-
Método: dinámica
En la figura, se han dibujado el esquema de las fuerzas sobre los cuerpos que intervienen en el movimiento. A partir de este esquema formulamos las ecuaciones de la dinámica de cada uno de los cuerpos.
Primero determinamos el sentido del movimiento. No es suficiente con comparar las masas de los cuerpos m1 y m2. Es necesario comparar los momentos de sus pesos. Si m1g·r1>m2g·r2, el movimiento tendrá el sentido indicado en la figura. Si m1g·r1<m2g·r2, el movimiento tendrá sentido contario.
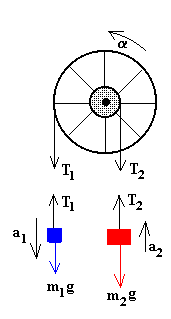
m1g-T1=m1a1
T2-m2g=m2a2
T1r1-T2r2=Iα
a1=α·r1
a2=α·r2
Como en los ejemplos anteriores, conocido el tiempo t que tarda en caer la pesa de masa m1 y la altura h1 desde la que cae, se determina la aceleración a1. Con los datos de los radios r1 y r2, se determina α y a2. A continuación T1, T2 y finalmente I.
Se completa la siguiente tabla y se despeja el momento de inercia desconocido
| Altura h1 | |
| Altura h2 | |
| Tiempo t | |
| Aceleración a1 | |
| Radio r1 | |
| Radio r2 | |
| Aceleración angular α | |
| Aceleración a2 | |
| Masa m1 de la pesa 1 | |
| Masa m2 de la pesa 2 | |
| Tensión de la cuerda T1 | |
| Tensión de la cuerda T2 | |
| Momento de inercia I |
|---|
Ejemplo, se introduce:
- Masa m1 de la primera pesa, 150 g
- Masa m2 de la segunda pesa 200 g.
- Radio r2 interior, 20 cm
¿En qué sentido gira?
Se pulsa el botón titulado Nuevo, y se mide el tiempo que tarda la pesa en recorrer una determinada altura. Se pulsa el botón titulado Ⅱ para detener el movimiento a una altura determinada. Se calcula el momento de inercia
Actividades
El radio exterior de la rueda se ha fijado en 30 cm
Comprobar los resultados de los tres ejercicios con los proporcionados por el programa interactivo.
Se muestra el balance energético mediante un diagrama de barras. A la izquierda, la energía cinética:
- En color gris, la energía cinética de rotación del disco.
- En color rojo, la energía cinética de la pesa roja
- En color azul, la energía cinética de la pesa azul
A la derecha, la energía potencial de las pesas roja y azul representadas mediante barras de color rojo y azul, respectivamente.
Práctica de laboratorio
Consiste en calcular el momento de inercia de un sólido en rotación alrededor de un eje fijo, mediante varias experiencias.
Experiencia 1
De las ecuaciones del movimiento, que hemos formulado al principio de esta página, despejamos el momento de inercia
En esta práctica, medimos con un sensor la aceleración angular α o bien, la aceleración a=α·r, siendo r=14.5 mm, el radio de la polea del sensor por el que pasa el hilo dejando caer una pesa de masa m=10 g. Tomamos como valor de la aceleración de la gravedad g=9.8 m/s2
En esta práctica utilizamos tres cuerpos: un disco, el mismo disco con un anillo y una varilla con dos pequeños cilindros acoplados a sus extremos. Comparamos los momentos de inercia medidos mediante la expresión de I con los calculados mediante las fórmulas más abajo y el teorema de Steiner
Los momentos de inercia respecto de un eje que pasa por el centro de masa de los cuerpos que se utilizan en esta experiencia son los siguientes
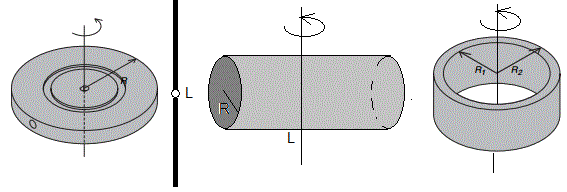
Los tres sólidos utilizados: una varilla con dos cilindros deslizantes, un disco, y el conjunto formado por el disco y anillo que encaja en el disco

Más abajo vemos una fotografía del sensor de rotación, de la varilla con los cilindros deslizantes, acoplado al sensor, y en la imagen inferior el disco acoplado al sensor. Se enrolla un hilo en una de las poleas del sensor de radio r=14.5 mm. El hilo pasa por una polea de masa despreciable, de su extremo libre cuelga una pesa de 10 g (5 gramos de la pesa cilíndrica de aluminio más 5 gramos del soporte). Los cuerpos se atornillan al eje vertical del sensor, tal como se muestra en la figura de la derecha en la que vemos un disco y un anillo encima

Disco
El disco tiene 121 g de masa y 4.75 cm de radio. El momento de inercia es I=0.121·0.04752/2=1.365·10-4 kgm2
El sensor de movimiento de rotación, nos produce una gráfica del ángulo girado θ en el eje vertical en función del tiempo t en el eje horizontal. Medimos la aceleración angular α=2A (dos veces el parámetro A del ajuste cuadrático)
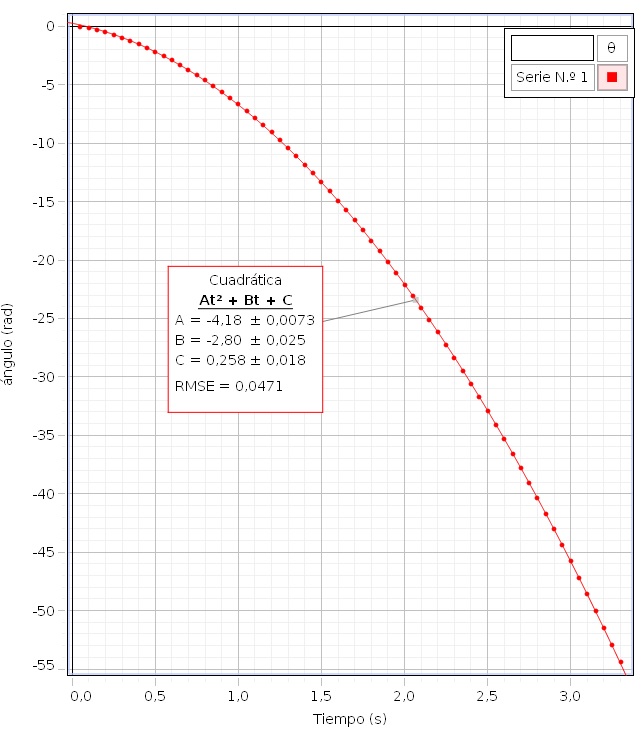
La aceleración lineal de la pesa a=2·4.18·0.0145=0.1212 m/s2. Calculamos el momento de inercia del disco
Disco con un anillo encima
La masa del anillo es 470.2 g, su radio interior es R1=2.65 cm, y su radio exterior es R2=3.8 cm. El momento de inercia del disco y del anillo es I=0.121·0.04752/2+0.4702·(0.0382+0.02652)/2=6.41·10-4 kgm2
El sensor de movimiento de rotación, nos produce una gráfica del ángulo girado θ en el eje vertical en función del tiempo t en el eje horizontal. Medimos la aceleración angular α=2A (dos veces el parámetro A del ajuste cuadrático)
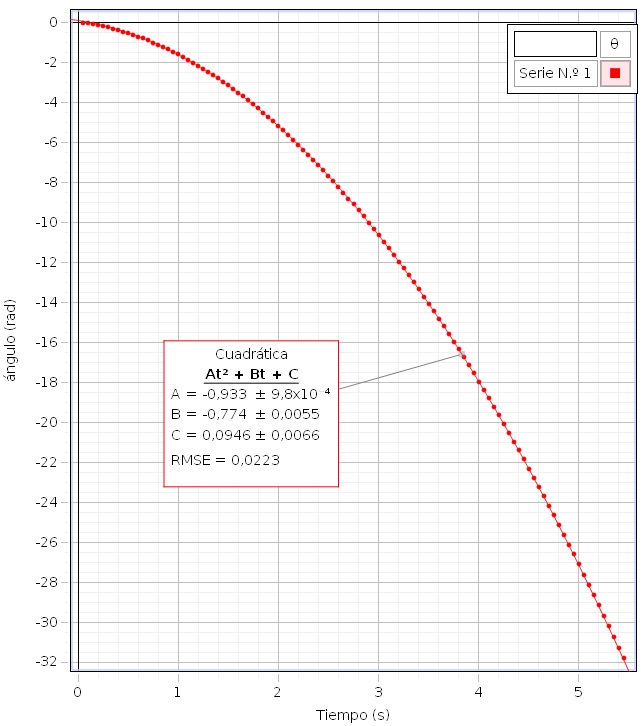
La aceleración lineal de la pesa a=2·0.933·0.0145=0.0270 m/s2. Calculamos el momento de inercia del disco y anillo
Varilla con dos cilindros deslizantes
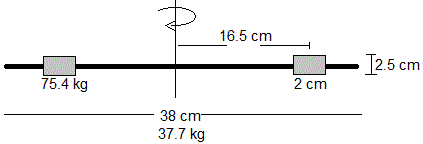
Los datos son los siguientes: longitud varilla, 38 cm, masa, 37.7 g. Longitud cilindros, 2 cm, radio de la base circular de los cilindros, 1.25 cm, masa, 75.4 g, distancia de los cilindros al eje de rotación, 16.5 cm. El momento de inercia respecto del eje perpendicular a la varilla y que pasa por su centro es
El sensor de movimiento de rotación, nos produce una gráfica del ángulo girado θ en el eje vertical en función del tiempo t en el eje horizontal. Medimos la aceleración angular α=2A (dos veces el parámetro A del ajuste cuadrático)
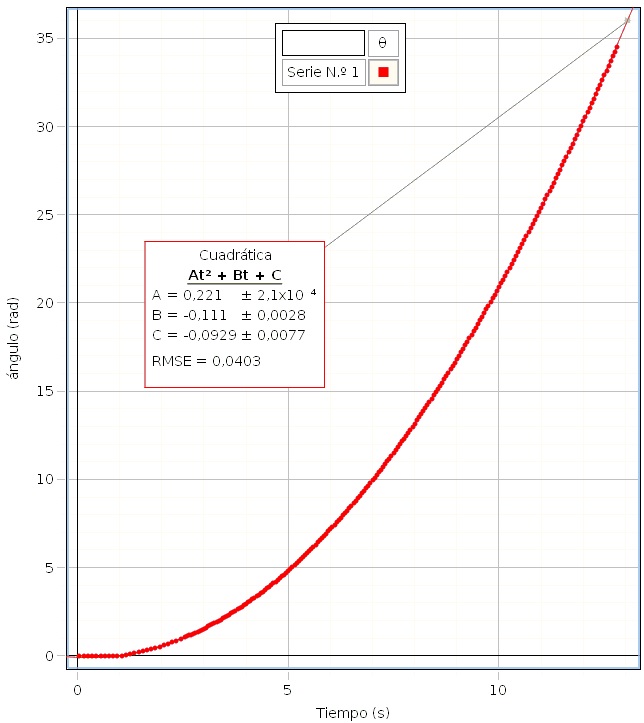
La aceleración lineal de la pesa a=2·0.221·0.0145=0.00641 m/s2. Calculamos el momento de inercia de la varilla con los cilindros
Experiencia 2
Dos pesas de masas 100 g y 120 g se unen mediante una cuerda y se colocan sobre una polea de 25.5 cm de radio. Se sueltan, el sólido rígido empieza a rotar. Se mide el tiempo que tarda la pesa mayor en caer una altura h=70 cm
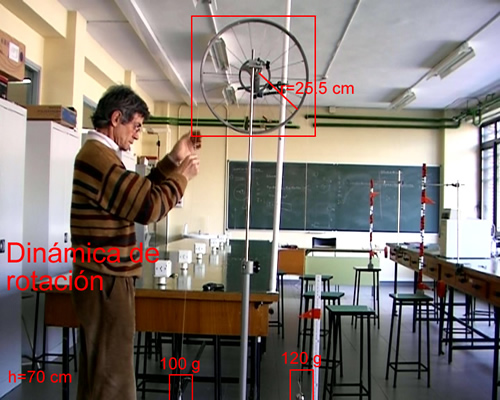
| Altura h | 0.7 m |
| Tiempo t | |
| Velocidad v | |
| Radio R | 0.255 m |
| Velocidad angular ω | |
| Masa m1 de la pesa 1 | 0.100 kg |
| Masa m2 de la pesa 2 | 0.120 kg |
| Momento de inercia I |
Experiencia 3
Se enrolla una cuerda alrededor de una polea de 2.9 cm de radio, se ata una pesa de 500 g al extremos libre de la cuerda y se suelta. El sólido rígido empieza a rotar. Se miede el tiempo que tarda la pesa en caer una altura h=70 cm

| Altura h | 0.85 m |
| Tiempo t | |
| Velocidad v | |
| Radio r | 0.029 m |
| Velocidad angular ω | |
| Masa m de la pesa | 0.5 kg |
| Momento de inercia I |
|---|

