Tumba de Carl Friedrich Gauss en Göttingen (Alemania). Busto de Gauss en la Universidad (Alte Aula)

Cuando el vector campo eléctrico $\overrightarrow{E}$ es constante en todos los puntos de una superficie S, se denomina flujo al producto escalar del vector campo por el vector superficie $\Phi =\overrightarrow{E}·\overrightarrow{S}$

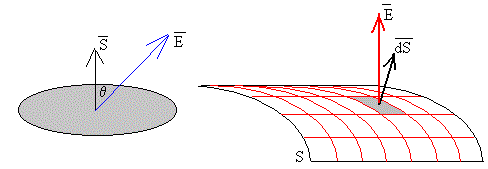
El vector superficie $\overrightarrow{S}$ es un vector que tiene por módulo el área de dicha superficie, la dirección es perpendicular al plano que la contiene.

Cuando el vector campo $\overrightarrow{E}$ y el vector superficie $\overrightarrow{S}$ son perpendiculares el flujo es cero

Si el campo no es constante o la superficie no es plana, se calcula el flujo a través de cada elemento $\overrightarrow{dS}$ de superficie, $\overrightarrow{E}\cdot \overrightarrow{dS}$ . El flujo a través de la superficie S, es

${\displaystyle \Phi =\underset{S}{{\displaystyle \int }}\overrightarrow{E}·\overrightarrow{dS}}$

La ley de Gauss afirma que el flujo del campo eléctrico a través de una superficie cerrada es igual al cociente entre la carga que hay en el interior de dicha superficie dividido entre ε₀.

${\displaystyle {{\displaystyle \oint }}^{\text{}}\overrightarrow{E}·\overrightarrow{dS}=\frac{q}{{\epsilon }_0}}$

Vamos a ver algunos ejemplos típicos de aplicación de la ley de Gauss

Campo eléctrico producido por un hilo rectilíneo cargado

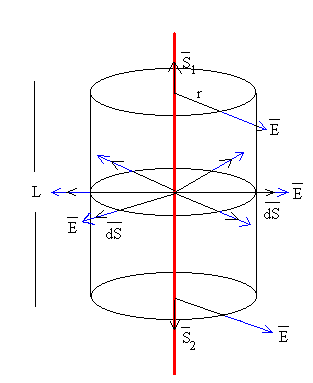
Para una línea indefinida cargada, la aplicación de la ley de Gauss requiere los siguientes pasos:

1. A partir de la simetría de la distribución de carga, determinar la dirección del campo eléctrico.

La dirección del campo es radial y perpendicular a la línea cargada

2. Elegir una superficie cerrada apropiada para calcular el flujo

Tomamos como superficie cerrada, un cilindro de radio r y longitud L.

• Flujo a través de las bases del cilindro: el campo $\overrightarrow{E}$ y el vector superficie $\overrightarrow{S_1}$ o $\overrightarrow{S_2}$ forman 90º, luego el flujo es cero.

• Flujo a través de la superficie lateral del cilindro: el campo $\overrightarrow{E}$ es paralelo al vector superficie $\overrightarrow{dS}$ . El campo eléctrico $\overrightarrow{E}$ es constante en todos los puntos de la superficie lateral

${\displaystyle \underset{S}{{\displaystyle \int }}\overrightarrow{E}·\overrightarrow{dS}=\underset{S}{{\displaystyle \int }}E·dS\cos 0º=E\underset{S}{{\displaystyle \int }}dS=E·2\pi rL}$

El flujo total es, E·2π rL

3. Determinar la carga que hay en el interior de la superficie cerrada

La carga que hay en el interior de la superficie cilíndrica de longitud L y radio r es q=λ L, donde λ es la carga por unidad de longitud.

4. Aplicar la ley de Gauss y despejar el módulo del campo eléctrico

${\displaystyle E2\pi rL=\frac{\lambda L}{{\epsilon }_0}E=\frac{\lambda }{2\pi {\epsilon }_{0}r}}$

Diferencia de potencial

Representamos el módulo del campo eléctrico E en función de la distancia radial r. El área sombreada es la diferencia de potencial

${\displaystyle V(r_0)-V(r)={\displaystyle \underset{r_0}{\overset{r}{\int }}E·dr}=\frac{\lambda }{2\pi {\epsilon }_0}{\displaystyle \underset{r_0}{\overset{r}{\int }}\frac{dr}{r}}=\frac{\lambda }{2\pi {\epsilon }_0}\ln \left(\frac{r}{r_0}\right)}$

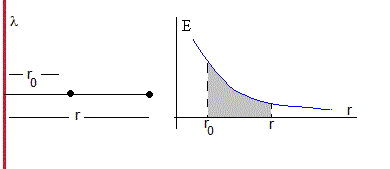
Campo eléctrico producido por un cilindro muy largo uniformente cargado

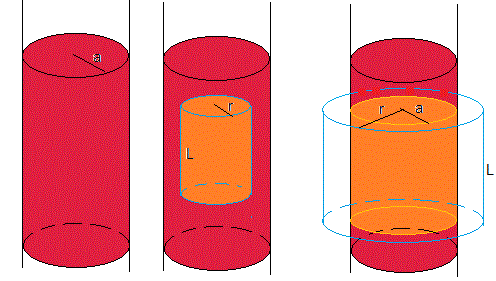
Un cilindro muy largo, macizo, de a=2 cm de radio, está uniformemente cargado en todo su volumen con una densidad de carga de 4·10^-6 C/m³.

Conocida la carga q contenida en una superficie cilíndrica de radio r y longitud L, determinamos el módulo del campo eléctrico E aplicando la ley de Gauss

${\displaystyle {{\displaystyle \oint }}^{\text{}}\overrightarrow{E}·\overrightarrow{dS}=\frac{q}{{\epsilon }_0}E=\frac{q}{2\pi {\epsilon }_{0}rL}}$

1. Campo eléctrico para r<a

Tomamos una superficie cilíndrica de radio r<2 cm y de altura L, véase la segunda figura. La carga contenida por esta superficie es

${\displaystyle \begin{array}{l}q=4·{10}^{-6}\pi r^{2}L=4\pi ·{10}^{-6}{r}^{2}L\\ E=72000\pi ·r\text{N/C}\end{array}}$

2. Campo eléctrico para r>a

Tomamos una superficie cilíndrica de radio r>2 cm y de altura L, véase la tercera figura. La carga contenida por esta superficie es

${\displaystyle \begin{array}{l}q=4·{10}^{-6}\pi {\left(0.02\right)}^{2}L=\pi ·1.6·{10}^{-9}L\hfill \\ E=\frac{28.8\pi }{r}\text{N/C}\hfill \end{array}}$

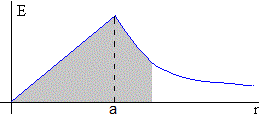
Calculamos la diferencial de potencial entre un punto situado en el eje del cilindro cargado y otro punto situado a una distancia de 15 cm de dicho eje.

Representamos el módulo del campo eléctrico E en función de la distancia radial r. El área sombreada es la diferencia de potencial

${\displaystyle V_0-V_{0.15}=\underset{0}{\overset{0.15}{{\displaystyle \int }}}E·dr=\underset{0}{\overset{0.02}{{\displaystyle \int }}}72000\pi r·dr+\underset{0.02}{\overset{0.15}{{\displaystyle \int }}}\frac{28.8\pi }{r}·dr=227.5\text{V}}$

Campo eléctrico producido por una distribución esférica y uniforme de carga

Para una distribución esférica y uniforme de carga, la aplicación de la ley de Gauss requiere los siguientes pasos:

1. A partir de la simetría de la distribución de carga, determinar la dirección del campo eléctrico.

La distribución de carga tiene simetría esférica, la dirección del campo es radial



2. Elegir una superficie cerrada apropiada para calcular el flujo

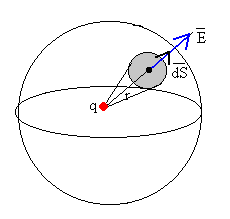
Tomamos como superficie cerrada, una esfera concéntricade radio r.

El campo eléctrico $\overrightarrow{E}$ es paralelo al vector superficie $\overrightarrow{dS}$ . Por simetría el campo es constante en todos los puntos de la superficie esférica de radio r, por lo que,

${\displaystyle \underset{S}{{\displaystyle \int }}\overrightarrow{E}·\overrightarrow{dS}=\underset{S}{{\displaystyle \int }}E·dS\cos 0º=E\underset{S}{{\displaystyle \int }}dS=E·4\pi r^2}$

El flujo total es, E·4πr²

3. Determinar la carga que hay en el interior de la superficie cerrada



• Para r<R. (figura de la izquierda)

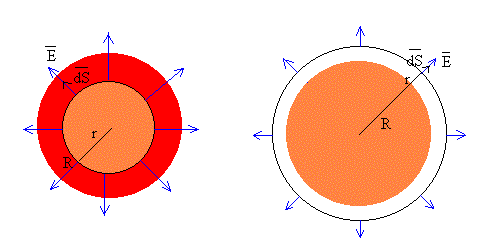
Si estamos calculando el campo en el interior de la esfera uniformemente cargada, la carga que hay en el interior de la superficie esférica de radio r es una parte de la carga total (en color rosado), que se calcula multiplicando la densidad de carga por el volumen de la esfera de radio r.

${\displaystyle q=Q\frac{r^3}{R^3}}$

• Para r>R (figura de la derecha)

Si estamos calculando el campo en el exterior de la esfera uniformemente cargada, la carga que hay en el interior de la superficie esférica de radio r es la carga total q=Q.

4. Aplicar la ley de Gauss y despejar el módulo del campo eléctrico

${\displaystyle E4\pi r^2=\frac{q}{{\epsilon }_0}}$

Se obtiene

${\displaystyle E=\frac{Qr}{4\pi {\epsilon }_0{R}^3}\text{( }r<R)E=\frac{Q}{4\pi {\epsilon }_0{r}^2}\text{( }r>R)}$

El campo en el exterior de una esfera cargada con carga Q, tiene la misma expresión que el campo producido por una carga puntual Q situada en su centro.

Potencial a una distancia r del centro de la esfera cargada

Se denomina potencial en un punto P a una distancia r del centro de la esfera cargada V(r) a la diferencia de potencial existente entre el punto P y el infinito V(r)-V(∞). Por convenio, se establece que en el infinito la energía potencial es cero.

Representamos el módulo del campo eléctrico E, en función de la distancia r al centro de la esfera cargada, en los intervalos 0< r<R y r>R

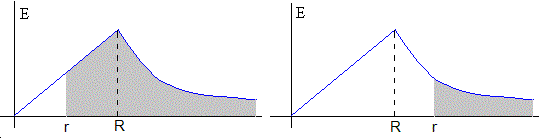
• r>R. Para hallar el potencial en un punto P que está fuera de la esfera cargada basta hallar el área sombreada (figura de la derecha)

${\displaystyle V={\displaystyle \underset{r}{\overset{\infty }{\int }}\frac{Q}{4\pi {\epsilon }_0{r}^2}dr=}\frac{Q}{4\pi {\epsilon }_{0}r}}$

• r<R. Para calcular el potencial en un punto P, en el interior de la esfera cargada, es necesario sumar dos áreas, (figura de la izquierda)

${\displaystyle V(r)={\displaystyle \underset{r}{\overset{R}{\int }}\frac{Qr}{4\pi {\epsilon }_0{R}^3}dr+}{\displaystyle \underset{R}{\overset{\infty }{\int }}\frac{Q}{4\pi {\epsilon }_0{r}^2}dr=}\frac{Q}{4\pi {\epsilon }_{0}r}=\frac{Q}{4\pi {\epsilon }_{0}R}\left(\frac{3}{2}-\frac{1}{2}\frac{r^2}{R^2}\right)}$

Modelo simple de átomo

En este modelo, el átomo está constituido por un núcleo, una carga puntual +Q, situada en el centro de una esfera de radio R, rodeado de una carga negativa -Q uniformemente distribuida en dicha esfera

La simetría de la distribución de carga nos indica que el campo eléctrico tendrá dirección radial. Tomamos como superficie cerrada, una esfera concéntrica de radio r.

El campo eléctrico $\overrightarrow{E}$ es paralelo al vector superficie $\overrightarrow{dS}$ . Por simetría el campo es constante en todos los puntos de la superficie esférica de radio r, por lo que,

${\displaystyle \underset{S}{{\displaystyle \int }}\overrightarrow{E}·\overrightarrow{dS}=\underset{S}{{\displaystyle \int }}E·dS\cos 0º=E\underset{S}{{\displaystyle \int }}dS=E·4\pi r^2}$

El flujo total es, E·4πr²

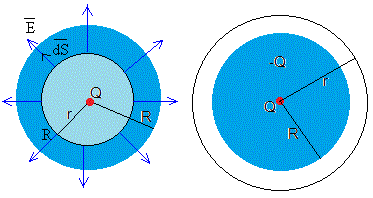
Para r<R. (figura de la izquierda)

La carga que hay en el interior de la superficie esférica de radio r es la carga puntual +Q y una parte de la carga -Q.

${\displaystyle q=Q-Q\frac{\frac{4}{3}\pi r^3}{\frac{4}{3}\pi R^3}=Q\left(1-\frac{r^3}{R^3}\right)}$

Para r>R. (figura de la derecha)

q=Q-Q=0

Aplicamos la ley de Gauss y despejamos el módulo del campo eléctrico

${\displaystyle E=\{\begin{array}{l}\frac{Q}{4\pi {\epsilon }_0{r}^2}\left(1-\frac{r^3}{R^3}\right),r<R\\ \mathrm{0,}r\ge R\end{array}}$

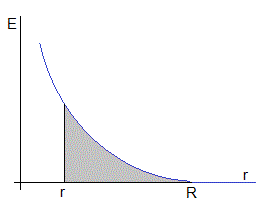
La diferencia de potencial entre dos puntos a una distancia r y R es área sombreada

${\displaystyle \begin{array}{l}V(r)-V(R)={\displaystyle \underset{r}{\overset{R}{\int }}\frac{Q}{4\pi {\epsilon }_0{r}^2}\left(1-\frac{r^3}{R^3}\right)dr=}\\ \frac{Q}{4\pi {\epsilon }_{0}R}\left(\frac{R}{r}+\frac{r^2}{2R^2}-\frac{3}{2}\right)\end{array}}$