Campo producido por un solenoide en un punto de su eje

Vamos a calcular el campo producido por el solenoide en un punto P situado en el eje del solenoide sumando el campo producido por las N espiras.

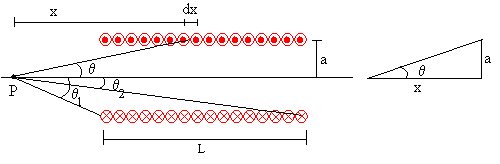
En la figura, tenemos un corte longitudinal de un solenoide de longitud L, formado por N espiras iguales de radio a.

En la página titulada, campo magnético producido por una espira, obtuvimos la expresión del campo magnético producido por una espira de radio a en un punto P de su eje distante x.

${\displaystyle B=\frac{{\mu }_{0}i{a}^2}{2{\left(\sqrt{a^2+x^2}\right)}^3}}$

Todas las espiras del solenoide producen en P un campo que tiene la misma dirección y sentido, pero distinto módulo, dependiendo de su distancia x al punto P.

El número de espiras que hay en el intervalo comprendido entre x y x+dx es dn=N·dx/L

Estas espiras producen en P un campo que es el producto del campo producido por una espira por el número dn de espiras

${\displaystyle dB=\frac{{\mu }_{0}i{a}^2}{2{\left(\sqrt{a^2+x^2}\right)}^3}\frac{N}{L}dx}$

Para integrar, tenemos que hacer el cambio de variable a=x·tanθ y teniendo en cuenta que, 1+tan²θ =1/cos²θ, simplificamos la integral

${\displaystyle B=\frac{{\mu }_{0}iN}{2L}{\displaystyle \underset{{\theta }_1}{\overset{{\theta }_2}{\int }}-\sin \theta ·d\theta }=\frac{{\mu }_{0}iN}{2L}\left(\cos {\theta }_2-\cos {\theta }_1\right)}$

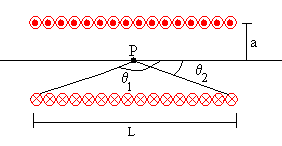
Si el solenoide es muy largo comparado con su radio a y si el punto P está situado en el centro, tendremos que ${\theta }_1\to \pi \text{y}{\theta }_2\to 0$. El campo B vale entonces

${\displaystyle B=\frac{{\mu }_{0}iN}{L}}$

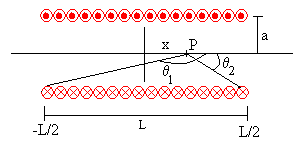
Representamos ahora, el campo B en unidades del campo en el centro del solenoide B₀, en función de la posición x del punto P, situando el origen de coordenadas en el centro del solenoide, tal como se muestra en la figura.

${\displaystyle \begin{array}{l}\begin{array}{l}B=\frac{{\mu }_{0}iN}{2L}(\cos {\theta }_2-\cos {\theta }_1)\hfill \\ \cos {\theta }_2=\frac{L/2-x}{\sqrt{{(L/2-x)}^2+a^2}}\cos {\theta }_1=\frac{-L/2-x}{\sqrt{{(-L/2-x)}^2+a^2}}\hfill \end{array}\\ B=\frac{{\mu }_{0}iN}{2L}\left(\frac{L/2-x}{\sqrt{{(L/2-x)}^2+a^2}}+\frac{L/2+x}{\sqrt{{(L/2+x)}^2+a^2}}\right)\end{array}}$

L=1; %longitud del solenoide
hold on
for a=[0.1,0.4] %radio
    B=@(x) ((L/2-x)./sqrt((L/2-x).^2+a^2)+(L/2+x)./sqrt((L/2+x).^2+a^2))/2;
    fplot(B,[-1,1]);
end
line([0.5,0.5],[0,B(0.5)],'lineStyle','--', 'color','k')
line([-0.5,-0.5],[0,B(-0.5)],'lineStyle','--', 'color','k')
hold off
grid on
xlabel('x')
legend('0.1','0.4','location','best')
ylabel('B/B_0')
title('Campo magnético en el eje de un solenoide')

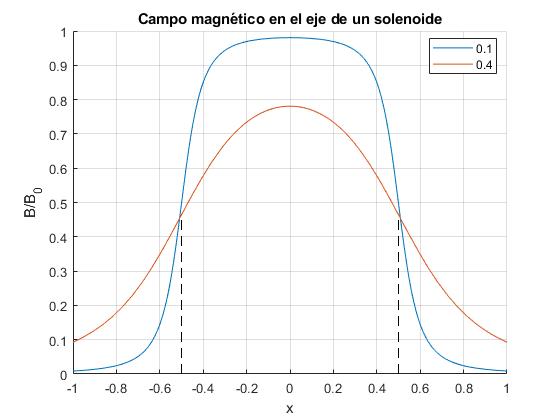
Cuando el radio a del solenoide es mucho más pequeño que su longitud L, el campo magnético es prácticamente uniforme en el interior del solenoide. Un poco más allá de los extremos del solenoide el campo magnético se reduce a cero

El solenoide. Ley de Ampère

Si suponemos que el solenoide es muy largo comparado con el radio de sus espiras, el campo es aproximadamente uniforme y paralelo al eje en el interior del solenoide y es nulo fuera del solenoide. En esta aproximación, es aplicable la ley de Ampère.

${\displaystyle {{\displaystyle \oint }}^{\text{}}\overrightarrow{B}·\overrightarrow{dl}={\mu }_{0}i}$

El primer miembro, es la circulación del campo magnético a lo largo de un camino cerrado y en el segundo miembro, el término i se refiere a la intensidad que atraviesa dicho camino cerrado.

Para determinar el campo magnético, aplicando la ley de Ampère, tomamos un camino cerrado ABCD que sea atravesado por corrientes. La circulación es la suma de cuatro contribuciones, una por cada lado.

${\displaystyle {{\displaystyle \oint }}^{\text{}}\overrightarrow{B}·\overrightarrow{dl}=\underset{A}{\overset{B}{{\displaystyle \int }}}\overrightarrow{B}·\overrightarrow{dl}+\underset{B}{\overset{C}{{\displaystyle \int }}}\overrightarrow{B}·\overrightarrow{dl}+\underset{C}{\overset{D}{{\displaystyle \int }}}\overrightarrow{B}·\overrightarrow{dl}+\underset{D}{\overset{A}{{\displaystyle \int }}}\overrightarrow{B}·\overrightarrow{dl}}$

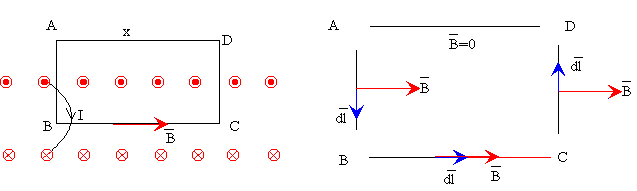
Examinaremos, ahora cada una de las contribuciones a la circulación:

1. Como vemos en la figura, la contribución a la circulación del lado AB es cero ya que bien $\overrightarrow{B}$ y $\overrightarrow{dl}$ son perpendiculares o bien, $\overrightarrow{B}$ es nulo en el exterior del solenoide.
2. Lo mismo ocurre en el lado CD.
3. En el lado DA la contribución es cero, ya que el campo en el exterior al solenoide es cero.
4. El campo es constante y paralelo al lado BC, la contribución a la circulación es Bx, siendo x la longitud de dicho lado.

La corriente que atraviesa el camino cerrado ABCD se puede calcular fácilmente:

Si hay N espiras en la longitud L del solenoide en la longitud x habrá Nx/L espiras. Como cada espira trasporta una corriente de intensidad i, la corriente que atraviesa el camino cerrado ABCD es Nx·i/L.

La ley de Ampère se escribe para el solenoide.

${\displaystyle Bx={\mu }_0\frac{Nx}{L}iB=\frac{{\mu }_{0}N}{L}i}$

Líneas de campo magnético

Para visualizar las líneas de campo magnético, se emplean limaduras de hierro. Este procedimiento es muy limitado y requiere bastante cuidado por parte del experimentador. Véase la fotografía al principio de esta página

En el programa interactivo se calcula, aplicando la ley de Biot-Savart, el campo magnético producido por cada espira en un punto fuera del eje. Posteriormente, determina el campo magnético resultante, sumando vectorialmente el campo producido por cada espira en dicho punto. Finalmente, se trazan las líneas del campo magnético que pasan por puntos equidistantes a lo largo del diámetro del solenoide.

Se representa las líneas del campo magnético de:

• Una espira circular
• Dos espiras, esta disposición simula las denominadas bobinas de Helmholtz, utilizadas en el laboratorio para producir campos magnéticos aproximadamente uniformes en la región entre las dos bobinas.
• Muchas espiras iguales y equidistantes, que simula el solenoide.

Se introduce

• El número de espiras N en el control titulado nº de espiras
• La separación entre las espiras, en el control titulado Separación

Se pulsa el botón titulado Nuevo

Campo magnético producido por una corriente de forma helicoidal en un punto de su eje

Las ecuaciones paramétricas de una hélice son

${\displaystyle \{\begin{array}{l}x=R\sin \theta \\ y=R\cos \theta \\ z=c\theta \end{array}}$

n=3;
fplot3(@(t) sin(t), @(t) cos(t),@(t) 0.2*t, [0,n*2*pi])
grid on
xlabel('x'); 
ylabel('y'); 
zlabel('z')
title('Hélice')

Representamos N=3 vueltas de una hélice de radio R=1 y avance c=0.2 a lo largo del eje Z

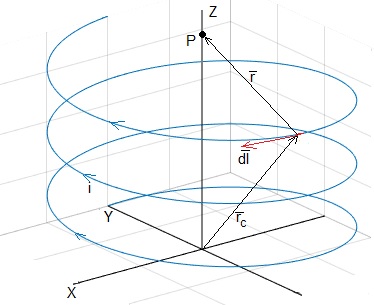
Después de N vueltas, la distancia entre el punto inicial (0,1,0) y el punto final (0,1, z) de la hélice es z=2πc·N, tal como se aprecia en la figura.

Aplicamos la ley de Biot para calcular el campo magnético producido en P por la corriente de forma helicoidal

${\displaystyle \overrightarrow{B}=\frac{{\mu }_{0}i}{4\pi }{\displaystyle \oint \frac{{\widehat{u}}_t\times {\widehat{u}}_r}{r^2}dl}=\frac{{\mu }_{0}i}{4\pi }{\displaystyle \oint \frac{\overrightarrow{dl}\times \overrightarrow{r}}{r^3}}}$

• La posición de elemento de corriente es

${\displaystyle \overrightarrow{r_c}=R\sin \theta \widehat{i}+R\cos \theta \widehat{j}+c\theta \widehat{k}}$

• El vector $\overrightarrow{dl}$ es tangente a la curva en el punto cuyo vecto posición es $\overrightarrow{r_c}$, por tanto

${\displaystyle \overrightarrow{dl}=\left(R\cos \theta \widehat{i}-R\sin \theta \widehat{j}+c\widehat{k}\right)d\theta }$

• La posición del punto P situado en el eje Z es $\overrightarrow{r_P}$

• La posición $\overrightarrow{r}$ del punto P relativa al elemento de corriente es

${\displaystyle \begin{array}{l}\overrightarrow{r}=\overrightarrow{r_P}-\overrightarrow{r_c}=-R\sin \theta \widehat{i}-R\cos \theta \widehat{j}+\left(z-c\theta \right)\widehat{k}\\ r^2=R^2+{\left(z-c\theta \right)}^2\end{array}}$

Efectuamos el producto vectorial

${\displaystyle \begin{array}{l}\overrightarrow{dl}\times \overrightarrow{r}=\left|\begin{array}{ccc}\widehat{i}& \widehat{j}& \widehat{k}\\ R\cos \theta & -R\sin \theta & c\\ -R\sin \theta & -R\cos \theta & z-c\theta \end{array}\right|d\theta =\\ \left(c\cos \theta -\left(z-c\theta \right)\sin \theta \right)Rd\theta \widehat{i}-\left(c\sin \theta +\left(z-c\theta \right)\cos \theta \right)Rd\theta \widehat{j}-R^{2}d\theta \widehat{k}\end{array}}$

Las componentes del campo magnético producido en P (0, 0, z) por una corriente en forma helicoidal de N vueltas

${\displaystyle \begin{array}{l}{B}_x=\frac{{\mu }_{0}iR}{4\pi }{\displaystyle \underset{0}{\overset{2\pi N}{\int }}\frac{c\cos \theta -\left(z-c\theta \right)\sin \theta }{{\left(R^2+{\left(z-c\theta \right)}^2\right)}^{3/2}}d\theta }\\ B_y=-\frac{{\mu }_{0}iR}{4\pi }{\displaystyle \underset{0}{\overset{2\pi N}{\int }}\frac{c\sin \theta +\left(z-c\theta \right)\cos \theta }{{\left(R^2+{\left(z-c\theta \right)}^2\right)}^{3/2}}d\theta }\\ B_z=-\frac{{\mu }_{0}i{R}^2}{4\pi }{\displaystyle \underset{0}{\overset{2\pi N}{\int }}\frac{d\theta }{{\left(R^2+{\left(z-c\theta \right)}^2\right)}^{3/2}}}\end{array}}$

Para resolver esta integral se hace el cambio, x=z-cθ, dx=-c·dθ

${\displaystyle {\displaystyle \int \frac{d\theta }{{\left(R^2+{\left(z-c\theta \right)}^2\right)}^{3/2}}=}-\frac{1}{c}{\displaystyle \int \frac{dx}{{\left(R^2+x^2\right)}^{3/2}}}}$

Se hace el cambio, x=Rtant, dx=R·dt/cos²t

${\displaystyle {\displaystyle \int \frac{dx}{{\left(x^2+R^2\right)}^{3/2}}}={\displaystyle \int \frac{R\frac{dt}{{\cos }^{2}t}}{R^3\frac{1}{{\cos }^{3}t}}}=\frac{1}{R^2}{\displaystyle \int \cos t·dt}=\frac{1}{R^2}\sin t}$

Deshacemos los cambios, teniendo en cuenta la relación trigonométrica

${\displaystyle \sin t=\frac{\tan t}{\sqrt{1+{\tan }^{2}t}}=\frac{\frac{x}{R}}{\sqrt{1+\frac{x^2}{R^2}}}=\frac{x}{\sqrt{x^2+R^2}}}$

El resultado es

${\displaystyle B_z=\frac{{\mu }_{0}i}{4\pi c}\left(\frac{z-2\pi Nc}{\sqrt{R^2+{\left(z-2\pi Nc\right)}^2}}-\frac{z}{\sqrt{R^2+z^2}}\right)}$

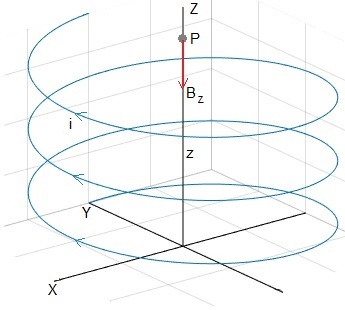
De acuerdo a la regla de la mano derecha, la componente B_z del campo magnético es negativa, apunta hacia el origen

Representamos la componente B_z del campo magnético, para los puntos del eje Z, situados entre el origen z=0 y z=2πc·N con N=10. Los valores obtenidos se han de multiplicar por μ₀i/(4π)=10^-7i, para expresar el campo magnético en el S. I. de unidades

n=10;
R=1;
c=0.2;
f=@(z) ((z-2*pi*c*n)./sqrt(R^2+(z-2*pi*c*n).^2)-z./sqrt(z.^2+R^2))/c;
fplot(f,[0,2*pi*c*n])
grid on
xlabel('z'); 
ylabel('B_z'); 
title('Componente B_z')

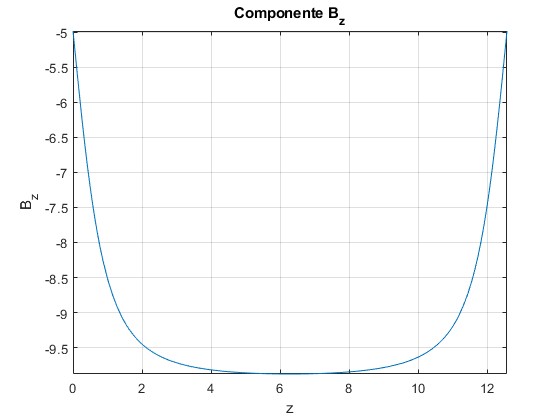
El campo magnético es casi constante en el interior de la corriente helicoidal, dismimuye rápidamente cerca de los extremos. Un comportamiento similar al estudiado en el primer apartado

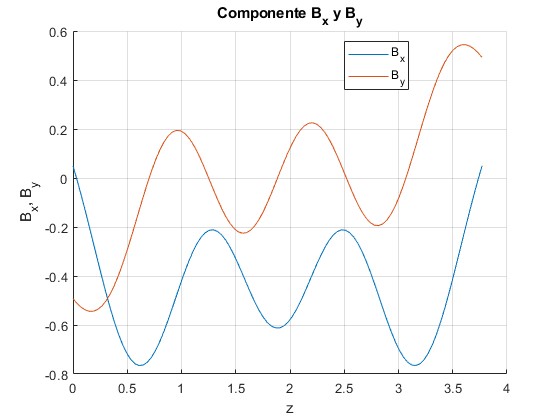
Las componentes B_x y B_y carecen de importancia, son pequeñas (en valor absoluto) frente a B_z. Representamos ambas componentes para N=3. Para cada valor de z, la integral se calcula utilizando el procedimiento numérico integral de MATLAB

n=3;
R=1;
c=0.2;
zz=linspace(0,n*c*2*pi,100);
Bx=zeros(1, length(zz));
By=zeros(1, length(zz));
k=1;
for z=zz
    f=@(x) (c*cos(x)-(z-c*x).*sin(x))./(R^2+(z-c*x).^2).^(3/2); %B_x
     Bx(k)=R*integral(f,0,2*pi*n);
     f=@(x) (c*sin(x)+(z-c*x).*cos(x))./(R^2+(z-c*x).^2).^(3/2); %B_y
     By(k)=-R*integral(f,0,2*pi*n);
   k=k+1;
end
hold on
plot(zz,Bx)
plot(zz,By)
hold off
grid on
xlabel('z'); 
legend('B_x', 'B_y','location','best')
ylabel('B_x, B_y'); 
title('Componente B_x y B_y')

Solenoide y corriente helicoidal

El campo magnético producido por un solenoide de longitud L y N espiras es

${\displaystyle B_s={\mu }_{0}i\frac{N}{L}}$

su dirección es paralela al eje del solenoide

Consideremos una corriente helicoidal de la misma longitud L=2πcN y N vueltas, la componente Z del campo magnético producido en un punto P del eje es

${\displaystyle B_z=\frac{{\mu }_{0}i}{4\pi \frac{L}{2\pi N}}\left(\frac{z-L}{\sqrt{R^2+{\left(z-L\right)}^2}}-\frac{z}{\sqrt{R^2+z^2}}\right)={\mu }_{0}i\frac{N}{2L}\left(\frac{z-L}{\sqrt{R^2+{\left(z-L\right)}^2}}-\frac{z}{\sqrt{R^2+z^2}}\right)}$

El cociente entre ambos campos es

${\displaystyle \frac{B_z}{B_s}=\frac{1}{2}\left(\frac{z-L}{\sqrt{R^2+{\left(z-L\right)}^2}}-\frac{z}{\sqrt{R^2+z^2}}\right)}$

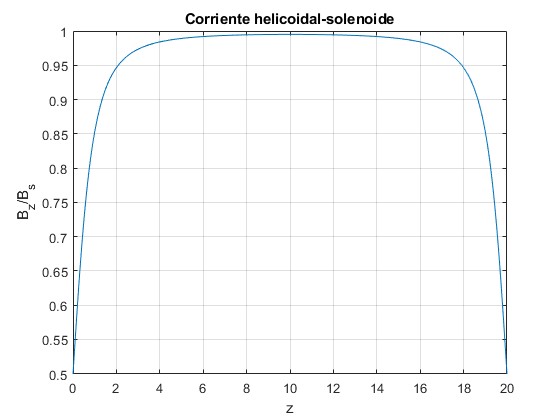
Comprobamos que cuando L>>R, B_z/B_s→1 en el interior de la corriente helicoidal

L=20;
R=1;
f=@(z) -((z-L)./sqrt(R^2+(z-L).^2)-z./sqrt(z.^2+R^2))/2;
fplot(f,[0,L])
grid on
xlabel('z'); 
ylabel('B_z/B_s'); 
title('Corriente helicoidal-solenoide')

Referencias

Richard Taylor. The On-Axis Magnetic Field for a Single, Helical Turn Coil. The Physics Teacher, Vol. 59, September 2021, pp. 455-458