Histéresis en un tubo en forma de U que gira alrededor de un eje vertical
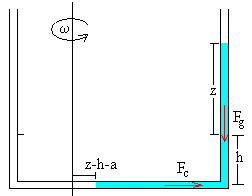
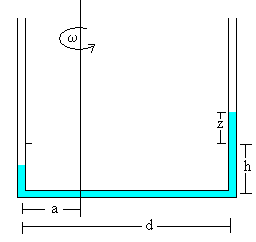
Supondremos que el tubo está formado por tres brazos rectos de la misma sección, uno horizontal y dos verticales. Se suelda los extremos del brazo horizontal de longitud d, con cada uno de los extremos de los dos brazos verticales. Supondremos el diámetro interior del tubo es despreciable comparado con la distancia d entre los dos brazos verticales.
Se produce el fenómeno de la histéresis, cuando el sistema puede existir en varios estados estables para valores dados de las variables externas (o parámetros de control) y que éstos se puede alcanzar por una variación lenta de los parámetros. Un ejemplo típico es la magnetización de un material ferromagnético por un campo magnético externo.
El comportamiento del sistema físico está descrito por la altura del líquido z en el brazo más alejado del eje de rotación por encima de la altura de equilibrio h. El parámetro que cambia es la velocidad angular de rotación ω. En ciertos casos, cuando se alcanzan valores críticos de velocidad angular de rotación, el comportamiento del sistema experimenta un salto. Por otra parte, el comportamiento del sistema no es el mismo cuando se incrementa la velocidad angular de rotación que cuando se disminuye.
Análisis en términos de fuerzas
Situación inicial
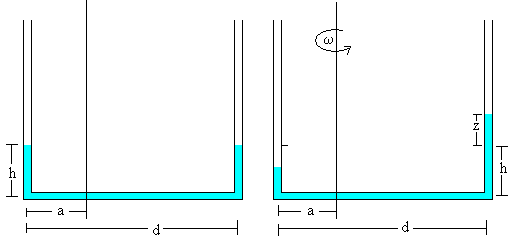
El tubo se llena con líquido hasta una altura h en los dos brazos verticales. Sea a<d/2 la distancia entre el eje de rotación y el brazo vertical más próximo.
Configuración A
Cuando se hace girar con velocidad angular ω alrededor del eje vertical, la columna de líquido asciende z en el brazo más alejado del eje y desciende la misma cantidad en la más cercano al eje. Vamos a calcular z a partir de las condiciones de equilibrio del líquido en los tres brazos.
Brazo horizontal
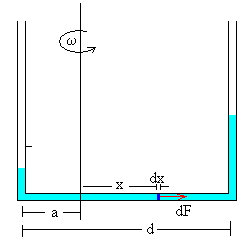
Al girar el tubo, la fuerza centrífuga actúa en los elementos del líquido situados en el brazo horizontal. La fuerza centrífuga que actúa sobre un elemento de masa dm situado a una distancia x del eje de rotación es
dFc=ω2·x·dm=ρAω2x·dx
donde ρ es la densidad del líquido y A la sección trasversal constante del tubo.
La fuerza centrífuga total sobre el líquido situado en el brazo horizontal a ambos lados del eje se obtiene integrando desde x=-a hasta x=d-a.
que es la diferencia de las dos fuerzas centrífugas que actúan sobre las porciones de líquido situadas a uno (0 a d-a) y otro lado (de 0 a a) del eje de rotación.
Brazos verticales
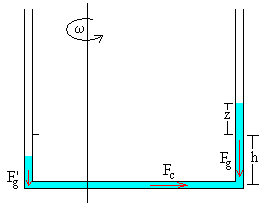
El peso del líquido contenido en el brazo vertical más alejado del eje de rotación es Fg=ρAg(h+z) y actúa en su centro de masa a una altura (h+z)/2
El peso del líquido contenido en el brazo vertical más cercano del eje de rotación es F’g=ρAg(h-z) y actúa en su centro de masa a una altura (h-z)/2
Equilibrio
En el equilibrio, la suma de fuerzas sobre el líquido contenido en el tubo debe ser cero
Fc+F'g-Fg=0
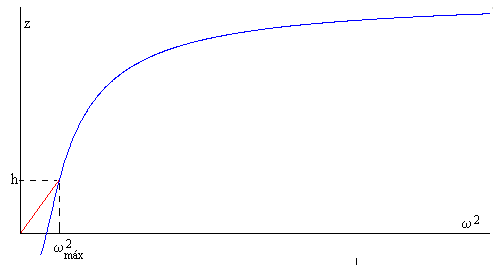
A medida que incrementamos la velocidad angular de rotación ω, la altura z de líquido por encima de la de equilibrio h, en el brazo vertical más alejado del eje de rotación, va creciendo proporcionalmente ω2 y decrece en el brazo más cercano al eje. Cuando z=h, desaparece el líquido en este brazo vertical. La velocidad angular ωmáx vale
Cuando la velocidad angular ω>ωmáx el líquido adopta la configuración B que describiremos a continuación.
Configuración B
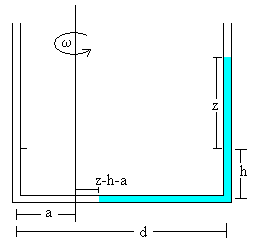
En la configuración B, el brazo más próximo al eje no contiene líquido. El brazo horizontal está parcialmente lleno, la distancia del eje de rotación al extremo de la columna de líquido es z-a-h, tal como se muestra en la figura
Como el fluido es incomprensible, la longitud total inicial de líquido es d+2h, por lo que en esta configuración:
-
la longitud del líquido en el brazo horizontal es d-(a+z-h-a)=d-z+h
-
en el brazo vertical más alejado del eje, h+z
-
En total, tenemos d+2h de líquido en el brazo horizontal y vertical del tubo en U
Brazo horizontal
La fuerza centrífuga sobre la porción de líquido en el tubo horizontal vale
Brazo vertical
El peso del líquido contenido en el brazo vertical es
Fg=ρAg(h+z)
En el equilibrio Fc=Fg
Cuando z=h, obtenemos
La recta que describe los estados de equilibrio de configuración A y la curva que describe los de la configuración B se encuentran en el punto (ω2, h)
Estados de equilibrio
En la figura, se representa la altura adicional z en el brazo vertical más alejado del eje en función del cuadrado de la velocidad angular ω2 de rotación, para los valores de
-
Distancia entre los brazos verticales, o longitud del tubo horizontal, d=2.0.
-
Distancia al eje de rotación, a=0.85
-
Altura inicial del líquido, h=0.6
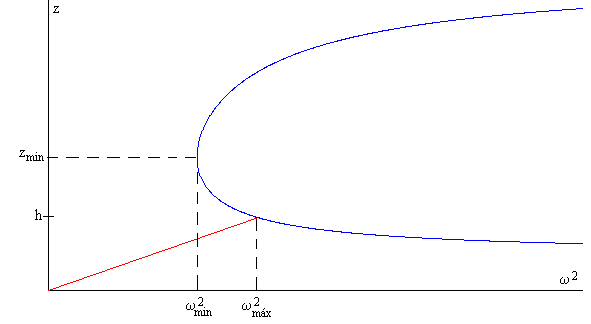
Configuración A.
El valor de la velocidad angular ω de rotación que hace que z=h, es decir, desaparezca el líquido del brazo vertical más cercano al eje de rotación es
Se representa la función
en el intervalo 0<ω<ωmáx, que es la línea recta de color rojo de la figura
Configuración B
La relación entre z y la velocidad angular de rotación ω es más compleja
y se representa por la curva de color azul de la figura
Despejamos z en función de ω2, obtenemos la ecuación de segundo grado
Las raíces de la ecuación son
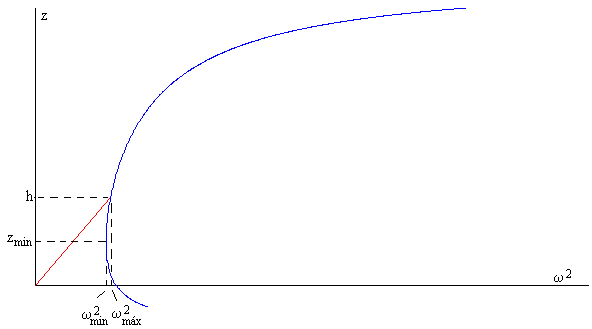
Para un valor dado de ω>ωmin, existen dos valores de z uno corresponde a un equilibrio estable y el otro inestable, tal como veremos en el análisis energético.
El valor de ωmin se obtiene cuando las raíces son iguales, es decir, cuando el discriminante es cero B2=C, y zmin=B
Si tomamos el signo positivo de la raíz, obtendríamos un valor de z negativo, en cambio el valor negativo la raíz da lugar a un valor z positivo
Para la velocidad angular
La altura adicional del líquido zmin en el brazo vertical más alejado del eje de rotación, que corresponde a esta velocidad angular es
Podemos obtener zmin de forma alternativa, derivando ω2 respecto de z en la expresión
e igualándola a cero,
Con los datos numéricos proporcionados al principio de este apartado h=0.6, a=0.85 y d=2.0.
d=2; %distancia entre los s verticales
a=0.85; %distancia del brazo izquierdo al eje de rotación
h=0.6; %altura inicial de líquido en ambos brazos
hold on
%configuración A
w2Max=4*9.8*h/(d*(d-2*a))
line([0,w2Max],[0,h]);
%configuración B
w2Min=9.8/(2*h+a-sqrt((2*h+d)*(2*h+2*a-d)))
w2=linspace(w2Min,50,200);
B=h+a-9.8./w2;
C=-d^2+2*d*a+2*a*h+h^2+2*9.8*h./w2;
z=B+sqrt(B.^2-C);
plot(w2,z);
z=B-sqrt(B.^2-C);
plot(w2,z);
hold off
xlabel('\omega^2');
ylabel('z');
title('Histéresis')
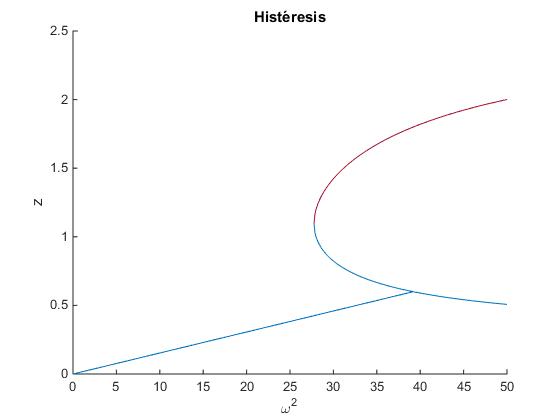
w2Max = 39.2000 w2Min = 27.7665
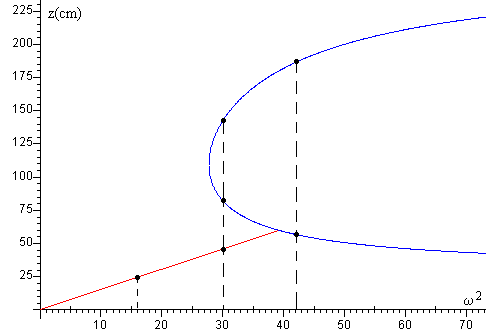
El ciclo de histéresis
En la figura, se muestra el ciclo de histéresis que sigue el líquido en el tubo en forma de U cuando se incrementa y luego, se disminuye la velocidad angular de rotación ω.
- En el eje vertical se representa la altura z del líquido en el brazo más alejado del eje de rotación, por encima de la altura inicial h.
- En el eje horizontal, el cuadrado de la velocidad angular de rotación ω2
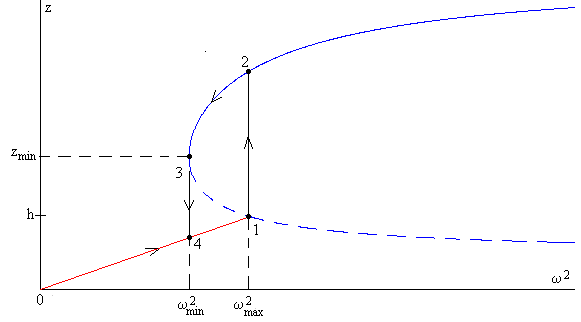
Cuando se incrementa la velocidad angular de rotación 0<ω<ωmáx, el tubo en U adopta la configuración A, la altura z del líquido en el brazo más alejado del eje de rotación, por encima de la altura de equilibrio h, se incrementa linealmente con ω2 (recta de color rojo)
Cuando la velocidad angular de rotación ω alcanza el valor ωmáx, (estado 1) desaparece el líquido del brazo vertical más cercano al eje de rotación z=h.
El sistema experimenta un salto (estado 2), estando descrito su comportamiento por la configuración B, la altura z que alcanza el líquido se obtiene poniendo ω=ωmáx en la raíz de la ecuación que describe la configuración B.
Si disminuye la velocidad angular, el comportamiento del sistema sigue el camino 2, 3. Cuando alcanza el estado 3, que corresponde al par de valores (ωmin, zmin) experimenta un nuevo salto al estado 4, descrito por la configuración A. Si disminuye aun más la velocidad angular, la altura z disminuye linealmente hasta que alcanza el estado inicial de equilibrio z=0, cuando ω=0.
Los distintos casos
Se debe tener en cuenta que la distancia del eje de rotación a un brazo vertical más cercano es a<d/2, siendo d la longitud del brazo horizontal.
-
Para que zmin sea real,
-
Para que exista histéresis, se tiene que cumplir que zmin>h, es decir
-
Condiciones para que se produzca histéresis
el radicando debe se positivo 2a+2h>d.
En la figura, se muestra la representación gráfica de z en función de ω2 para h=0.6, a=0.3 y d=2.0, que no cumple esta condición y por tanto, no existe zmin.
En la figura, se muestra la representación gráfica de z en función de ω2 para h=0.8, a=0.4 y d=2.0. Existe zmin, pero no se cumple que zmin>h
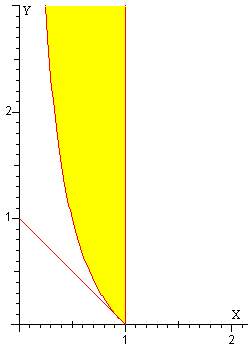
Las condiciones para que haya histéresis se pueden expresar mediante el sistema de inecuaciones
que delimitan la región coloreada de amarillo en el primer cuadrante del plano X, Y tal como se muestra en la figura.
Cuando seleccionamos un par de valores (a, h) que corresponden a un punto del plano (x, y) interior de la región amarilla se obtiene una representación grafica de z en función de ω2 similar a la de la figura al principio de este apartado. El sistema presenta histéresis.
Análisis energético. Estabilidad
En los apartados anteriores, hemos estudiado los posibles estados de equilibrio del sistema para una velocidad angular de rotación dada ω. El análisis energético nos permite examinar si el estado de equilibrio considerado es estable o inestable.
Energía potencial centrífuga
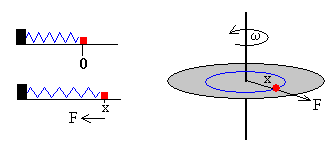
La fuerza centrífuga que actúa sobre una partícula de masa m situada a una distancia x del eje de rotación es
F=m ω2·x =m ω2x
Se trata de una fuerza dependiente de la posición x de la partícula, similar a la que ejerce un muelle elástico, es por lo tanto, una fuerza conservativa.
-
La fórmula de la energía potencial asociada a la fuerza que ejerce el muelle F=-kx es
-
La fórmula de energía potencial asociada a la fuerza centrífuga F=mω2x es
Situamos el nivel cero de energía potencial gravitatoria a la altura del brazo horizontal y el nivel cero de la energía potencial centrífuga en el eje de rotación
Configuración A
Energía potencial gravitatoria
La masa del líquido contenido en el brazo vertical más alejado del eje de rotación es ρA(h+z), su centro de masa se encuentra a una altura (h+z)/2
La masa de líquido contenido en el brazo vertical más cercano del eje de rotación es ρA(h-z), su centro de masa se encuentra a una altura (h-z)/2
La energía potencial gravitatoria del líquido contenido en los dos brazos verticales es
La energía potencial gravitatoria del líquido contenido en el brazo horizontal es cero.
Energía potencial centrífuga
Calculamos primero la energía potencial centrífuga del líquido contenido en el brazo vertical más cercano al eje de rotación cuyo radio es a, y la del líquido contenido en el brazo vertical más alejado del eje de rotación cuyo radio es d-a,
La energía potencial centrífuga del líquido contenido en el brazo horizontal, es la suma de la energía potencial de cada uno de los elementos de masa dm que distan x del eje de rotación.
La energía potencial total del líquido en la configuración A es
Ep(z)=E1c+E2c+Eg
Configuración B
Energía potencial gravitatoria

El brazo vertical más cercano del eje de rotación no tiene líquido alguno
La masa del líquido contenido en el brazo vertical más alejado del eje de rotación es ρA(h+z), su centro de masa se encuentra a una altura (h+z)/2
La energía potencial gravitatoria del líquido contenido en este brazo es
La energía potencial gravitatoria del líquido contenido en el brazo horizontal es cero.
Energía potencial centrífuga
Calculamos la energía potencial centrífuga del líquido contenido en el brazo vertical más alejado del eje de rotación cuyo radio es d-a,
La energía potencial centrífuga del líquido contenido en el brazo horizontal parcialmente lleno, es la suma de la energía potencial de cada uno de los elementos de masa dm que distan x del eje de rotación.
La energía potencial total del líquido en la configuración B es
Ep(z)=E1c+E2c+Eg
Se comprueba que E(z) es una función continua y tienen un único valor para z=h, es decir,
EA(h)=EB(h)
Ejemplos:
-
Distancia entre los brazos verticales, o longitud del tubo horizontal, d=2.0.
-
Distancia al eje de rotación, a=0.85
-
Altura inicial del líquido, h=0.6
En el apartado titulado "Estados de equilibrio" hemos calculado ωmin=5.27 rad/s y ωmáx=6.26 rad/s.
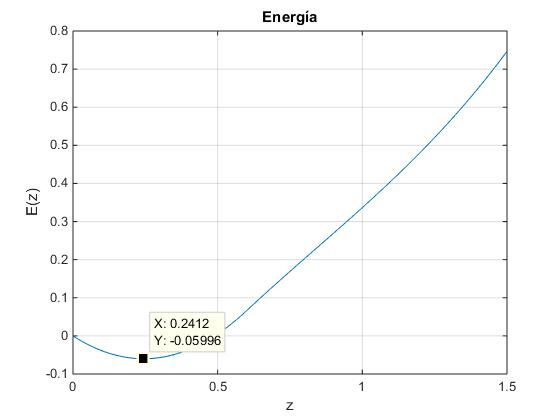
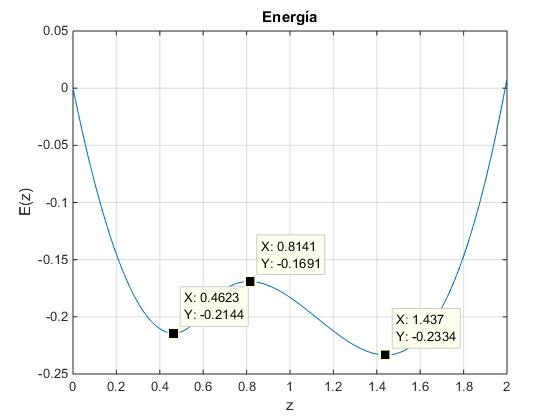
Vamos a representar E(z) para varios valores de la velocidad angular ω: 4, 5.5 y 6.5 rad/s
d=2; %distancia entre los brazos verticales
a=0.85; %distancia del brazo iqzquierdo al eje de rotación
h=0.6; %altura inicial de líquido en ambas brazos
w2=4^2; %cambiar aquí la velocidad angular de rotación
E1=@(z) z.^2-w2*(d^2-2*a*d)*z/(2*9.8)+
h^2-w2*(d^3-3*a*d^2+3*a^2*d+6*h*a^2+3*h*d^2-6*a*h*d)/(6*9.8);
E2=@(z) w2*z.^3/(6*9.8)+(1-w2*(h+a)/9.8)*z.^2/2+
(h+w2*(h+d)*(h+2*a-d)/(2*9.8))*z+h^2/2-w2*((d-a)^3
+(h+a)^3+3*(d-a)^2*h)/(6*9.8);
z=linspace(0,1.5,200);
E=(z<h).*E1(z)+(z>=h).*E2(z);
plot(z,E-E1(0))
grid on
xlabel('z');
ylabel('E(z)');
title('Energía')
Como vemos en la figura,
-
la recta ω=4 corta a la función que describe la configuración A, en un punto.
-
la recta ω=5.5 corta a la función que describe la configuración A en un punto y la B, en dos puntos.
-
la recta ω=6.5 corta a la función que describe la configuración B en dos puntos.
Vamos a estudiar la naturaleza (estable o inestable) de los estados (ω, z) del sistema señalados en la figura por puntos de color negro.
-
En la figura, se muestra E(z) para ω=4 rad, ω<ωmin
-
En la figura, se muestra E(z) para ω=5.5 rad, ωmin<ω<ωmáx
-
En la figura, se muestra E(z) para ω=6.5 rad, ω>ωmáx
-
Una figura similar de E(z) se obtiene para ωmáx=6.26 rad
-
Una figura similar de E(z) se obtiene para ωmin=5.27 rad,
La posición de equilibrio para la configuración A, se calcula mediante la fórmula
La posición de equilibrio para la configuración A se calcula mediante la fórmula
Las posiciones de equilibrio para la configuración B se calculan mediante la fórmula
B=1.126, C=1.169
z2=0.81, z3=1.44
Como vemos z2 corresponde a un máximo local y es un estado inestable. El sistema puede estar bien, en el estado z1 descrito por la configuración A o bien, en el estado z3, descrito por la configuración B.
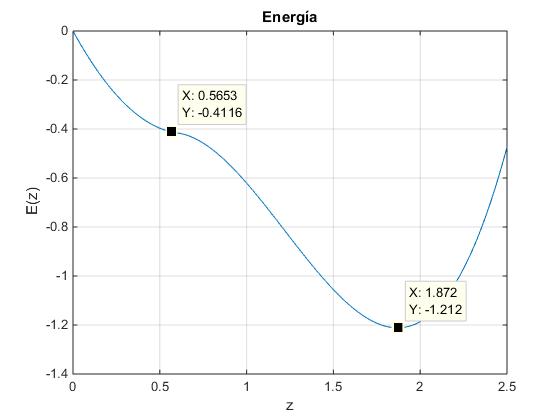
Las posiciones de equilibrio para la configuración B (ω>ωmáx) son
B=1.218, C=1.058
z2=0.57, z3=1.87
Como vemos z3 corresponde a un mínimo local y es una posición estable
La posición de equilibrio para la configuración A vale
z1=0.60
Las posiciones de equilibrio para la configuración B son
B=1.20, C=1.08
z2=0.6, z3=1.80
Como vemos, el sistema puede pasar fácilmente mediante alguna pequeña perturbación, del estado z1 descrito por la configuración A, al estado z3 descrito por la configuración B.
La posición de equilibrio para la configuración A vale
z1=0.42
Las posiciones de equilibrio para la configuración B son
B=1.20, C=1.08
z2=1.10, z3=1.10
Como vemos el sistema puede pasas fácilmente mediante alguna pequeña perturbación, del estado z3 descrito por la configuración B, al estado z1 descrito por la configuración A.
Referencias
Denardo B., Barber B., Folley C., Wright W., Nonfrictional hysteresis in a rotating U-tube. Am. J. Phys. 57 (12) December 1989, pp. 1126-1130

