Ecuación de la continuidad

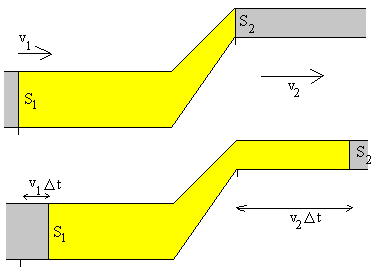
Consideremos una porción de fluido en color amarillo en la figura, el instante inicial t y en el instante t+Δt.

En un intervalo de tiempo Δt la sección  S₁ que limita a la porción de fluido en la tubería inferior se mueve hacia la derecha Δx₁=v₁Δt. La masa de fluido desplazada hacia la derecha es Δm₁=ρ·S₁Δx₁=ρS₁v₁Δt.

Análogamente, la sección S₂ que limita a la porción de fluido considerada en la tubería superior se mueve hacia la derecha  Δx₂=v₂Δt. en el intervalo de tiempo Δt. La masa de fluido desplazada es Δm₂=ρS₂v₂ Δt. Debido a que el flujo es estacionario la masa que atraviesa la sección S₁ en el tiempo Δt, tiene que ser igual a la masa que atraviesa la sección S₂ en el mismo intervalo de tiempo. Luego

v₁S₁=v₂S₂

Esta relación se denomina ecuación de continuidad.

En la figura, el radio del primer tramo de la tubería es el doble que la del segundo tramo, luego la velocidad del fluido en el segundo tramo es cuatro veces mayor que en el primero.

Ejemplo:

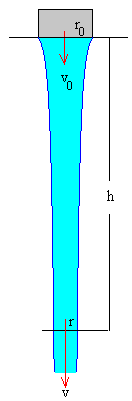
Cuando se abre poco a poco un grifo, se forma un pequeño chorro de agua, un hilo cuyo radio va disminuyendo con la distancia al grifo y que al final, se rompe formando gotas.

La ecuación de continuidad nos proporciona la forma de la superficie del chorrito de agua que cae del grifo, tal como apreciamos en la figura.

La sección trasversal del chorro de agua cuando sale del grifo es S₀ y la velocidad del agua es v₀. Debido a la acción de la gravedad la velocidad v del agua se incrementa. A una distancia h del grifo la velocidad es

${\displaystyle v^2=v_0^2+2gh}$

Aplicando la ecuación de continuidad

${\displaystyle \begin{array}{l}{S}_0{v}_0=Sv\\ \pi r_0^2{v}_0=\pi r^{2}v\end{array}}$

Despejamos el radio r del hilo de agua en función de la distancia h al grifo.

${\displaystyle r=r_0\sqrt[4]{\frac{v_0^2}{v_0^2+2gh}}}$

Ecuación de Bernoulli. Estado estacionario

Evaluemos los cambios energéticos que ocurren en la porción de fluido señalada en color amarillo, cuando se desplaza a lo largo de la tubería. En la figura, se señala la situación inicial y se compara la situación final después de un tiempo Δt. Durante dicho intervalo de tiempo, la cara posterior S₂ se ha desplazado v₂ Δt y la cara anterior S₁ del elemento de fluido se ha desplazado v₁Δt hacia la derecha.

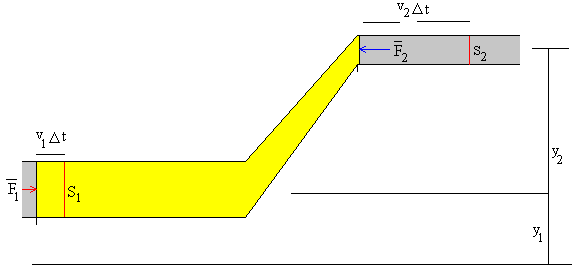
El elemento de masa Δm se puede expresar como Δm=ρS₂v₂Δt=ρ S₁v₁Δt=ρΔV

Comparando la situación inicial en el instante t y la situación final en el instante t+Δt. Observamos que el elemento Δm incrementa su altura, desde la altura y₁ a la altura y₂

• La variación de energía potencial es

ΔE_p=Δm·gy₂-Δm·gy₁=ρΔV·(y₂-y₁)g

El elemento Δm cambia su velocidad de v₁ a v₂,

• La variación de energía cinética es

${\displaystyle \Delta E_k=\frac{1}{2}\Delta m{v}_2^2-\frac{1}{2}\Delta m{v}_1^2=\frac{1}{2}\rho \Delta V\left(v_2^2-v_1^2\right)}$

El resto del fluido ejerce fuerzas debidas a la presión sobre la porción de fluido considerado, sobre su cara anterior y sobre su cara posterior F₁=p₁S₁ y F₂=p₂S₂.

La fuerza F₁ se desplaza Δx₁=v₁Δt. La fuerza y el desplazamiento son del mismo signo

La fuerza F₂ se desplaza Δx₂=v₂ Δt. La fuerza y el desplazamiento son de signos contrarios.

• El trabajo de las fuerzas exteriores es W_ext=F₁ Δx₁- F₂ Δx₂=(p₁-p₂) ΔV

El teorema del trabajo-energía nos dice que el trabajo de las fuerzas exteriores que actúan sobre un sistema de partículas modifica la energía del sistema de partículas, es decir, la suma de las variaciones de la energía cinética y la energía potencial del sistema de partículas

W_ext=E_f-E_i=(E_k+E_p)_f-(E_k+E_p)_i=ΔE_k+ΔE_p

Simplificando el término ΔV y reordenando los términos obtenemos la ecuación de Bernoulli

${\displaystyle p_1+\rho g{y}_1+\frac{1}{2}\rho v_1^2=p_2+\rho g{y}_2+\frac{1}{2}\rho v_2^2}$

Efecto Venturi

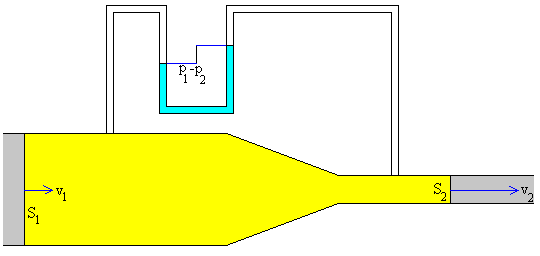
Cuando el desnivel es cero, la tubería es horizontal. Tenemos entonces, el denominado tubo de Venturi, cuya aplicación práctica es la medida de la velocidad del fluido en una tubería. El manómetro mide la diferencia de presión entre las dos ramas de la tubería.

La ecuación de continuidad se escribe

v₁S₁=v₂S₂

Que nos dice que la velocidad del fluido en el tramo de la tubería que tiene menor sección es mayor que la velocidad del fluido en el tramo que tiene mayor sección. Si S₁>S₂, se concluye que v₁<v₂.

La ecuación de Bernoulli con y₁=y₂

${\displaystyle p_1+\frac{1}{2}\rho v_1^2=p_2+\frac{1}{2}\rho v_2^2}$

Como la velocidad en el tramo de menor sección es mayor, la presión en dicho tramo es menor.

Si v₁<v₂ se concluye que p₁>p₂. El líquido manométrico desciende por el lado izquierdo y asciende por el derecho

Obtenemos las velocidades v₁ y v₂ en cada tramo de la tubería a partir de la lectura de la diferencia de presión p₁-p₂ en el manómetro.

${\displaystyle v_2=S_1\sqrt{\frac{2(p_1-p_2)}{\rho \left(S_1^2-S_2^2\right)}}}$

Ejemplo:

Determinar la velocidad del agua en ambos tramos de la tubería, sabiendo que:

• Radio del tramo izquierdo de la tubería, 20 cm.
• Radio del tramo derecho de la tubería, 5 cm.
• Medida de la diferencia de presión, 1275 Pa.

Los datos son:

S₁=π(0.2)² m², S₂=π(0.05)² m², ρ=1000 kg/m³, y p₁-p₂=1275 Pa.

Empleando la expresión anterior, obtenemos el valor de v₂=1.6 m/s. Calculamos v₁ a partir de la ecuación de continuidad (v₁S₁=v₂S₂) obteniendo v₁=0.1 m/s ó 10 cm/s.

Introducimos en el programa interactivo los siguientes datos y comprobamos el resultado:

• Radio del tramo izquierdo de la tubería, 20 cm.
• Velocidad del fluido en el tramo izquierdo, 10 cm/s
• Diferencia de alturas entre los dos tramos, 0

Actividades

Se introduce

• El radio del tramo izquierdo de la tubería, en el control titulado Radio.
• El radio del tramo derecho está fijado en 5 cm.
• El valor de la velocidad del tramo izquierdo, en el control titulado Velocidad.
• El desnivel, (un número positivo, nulo o negativo) o diferencia de alturas entre los dos tramos, en el control titulado Desnivel.

Se pulsa el botón titulado Nuevo

El valor de la velocidad en el tramo derecho se obtiene aplicando la ecuación de continuidad. Si el radio del tramo izquierdo es el doble que el radio del tramo derecho, la velocidad en el tramo derecho es cuatro veces mayor que en el izquierdo. Es decir, mientras que la sección anterior S₁ del elemento de fluido se desplaza 10 cm, la sección posterior S₂ se desplaza 40.

A continuación, nos fijaremos en los cambios energéticos.

A medida que el elemento de fluido (coloreado de amarillo) se mueve hacia la derecha su energía cambia. En la parte inferior izquierda, se muestra la variación de energía cinética, de energía potencial y el trabajo de las fuerzas exteriores (que ejerce el resto del fluido sobre el elemento de fluido considerado). Las fuerzas exteriores se señalan mediante flechas. Comprobamos que la suma de las variaciones de energía cinética y potencial nos da el trabajo de las fuerzas exteriores.

Ecuación de Bernoulli. Estado no estacionario

Consideremos una porción infinitesimal de tubo de sección A que contiene un líquido de densidad ρ moviéndose con velocidad v. La coordenada s se mide a lo largo del eje del tubo, de modo que dicha porción está comprendida entre s y s+ds. La diferencia de alturas entre los extremos del eje de la porción de tubo es dy=ds·sinθ

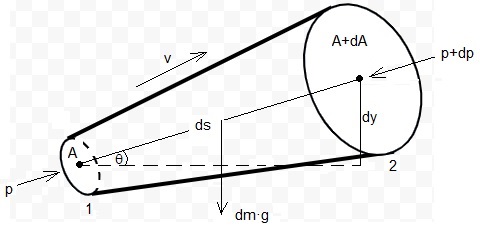
La presión que ejerce el resto del líquido sobre la sección izquierda es p y la presión sobre la sección derecha es p+dp.

La masa de líquido contenida en la porción de tubo es dm=ρA·ds.

Las fuerzas que actúan sobre la porción a lo largo de su eje son:

• pA-(p+dp)A=-A·dp, debido a la presión
• -dm·gsinθ, componente del peso a lo largo del eje del tubo

La ecuación del movimiento es

${\displaystyle \begin{array}{l}dm\frac{dv}{dt}=-Adp-dm·g\sin \theta \\ \left(\rho Ads\right)\frac{dv}{dt}=-Adp-\rho A·g·dy\\ \rho Ads\left(\frac{\partial v}{\partial s}\frac{ds}{dt}+\frac{\partial v}{\partial t}\right)=-A\frac{\partial p}{\partial s}ds-\rho Ag\frac{\partial y}{\partial s}ds\end{array}}$

El término $\frac{\partial v}{\partial t}$ es el no estacionario y v=ds/dt es la velocidad del líquido en la porción de tubo

${\displaystyle v\frac{\partial v}{\partial s}+\frac{\partial v}{\partial t}=-\frac{1}{\rho }\frac{\partial p}{\partial s}-g\frac{\partial y}{\partial s}}$

El flujo Q (masa de líquido que pasa a través de la sección A en la unidad de tiempo) es

${\displaystyle Q=\frac{dm}{dt}=\rho Av}$

que es independiente de s por la ecuación de continuidad

${\displaystyle \frac{dQ}{dt}=\frac{\partial Q}{\partial t}=\rho A\frac{\partial v}{\partial t}}$

Sustituyendo

${\displaystyle \begin{array}{l}-\frac{1}{\rho }\frac{\partial p}{\partial s}-g\frac{\partial y}{\partial s}=v\frac{\partial v}{\partial s}+\frac{1}{\rho A}\frac{dQ}{dt}\\ -\frac{\partial p}{\partial s}-\rho g\frac{\partial y}{\partial s}-\rho v\frac{\partial v}{\partial s}=\frac{1}{A}\frac{dQ}{dt}\end{array}}$

Integrando entre los extremos 1 y 2 de una porción de tubo

${\displaystyle {\left\{-p-\rho gy-\frac{1}{2}\rho v^2\right\}}_1^2=\frac{dQ}{dt}{\displaystyle \underset{1}{\overset{2}{\int }}\frac{ds}{A(s)}}}$

La ecuación de Bernoulli para un fluido en régimen laminar, incompresible y no viscoso, suponiendo que el flujo Q a través de una seccción A del tubo depende del tiempo, es

${\displaystyle \left(p_1+\rho g{y}_1+\frac{1}{2}\rho v_1^2\right)-\left(p_2+\rho g{y}_2+\frac{1}{2}\rho v_2^2\right)=\frac{dQ}{dt}{\displaystyle \underset{1}{\overset{2}{\int }}\frac{ds}{A(s)}}}$

En el estado estacionario el flujo Q es constante e independiente del tiempo, obteniendo la ecuación de Bernoulli del apartado anterior

Aplicaremos esta ecuación en las páginas tituladas

Vaciado de un depósito abierto

Oscilaciones de un líquido contenido en un tubo en U de sección variable

Referencias

Grubelnik V., Marhl M., Drop formation in a falling stream of liquid. Am. J. Phys. 73 (5) May 2005, pp. 415-419

Carl E Mungan, Garth A Sheldon-Coulson. Liquid oscillating in a U-tube of variable cross section. Eur. J. Phys.42(2021) 025008

Artículo disponible en la dirección: https://www.usna.edu/Users/physics/mungan/Publications/Publications.php#fndtn-panel120162017